基于模糊专家系统的电能质量治理决策支持系统
2019-03-19,,,,
,,,,
(1.浙江工业大学 信息工程学院,浙江 杭州 310023;2.三亚航空旅游职业学院 机电工程学院,海南 三亚 572000)
近年来,随着各种先进电力电子器件的广泛使用,分布式能源(Distributed generation, DG)高渗透率接入,电网电能质量(Power quality, PQ)问题变得越来越复杂。由于各电网结构、组成和运行特性差异甚大,其电能质量特性各异[1-2]。对于非专家级人员(如普通电网员工、DG或微网用户),如何在众多PQ治理方案中进行合理选择,使得方案性价比最优,非常具有挑战性。因此,开展PQ治理决策支持系统研究,具有重要的意义。
目前,不少国内外专家对PQ治理问题进行了相关研究,成果主要包括技术和经济两个层面。从技术层面看,例如陈磊等[3]给出了解决低压配电网的三相不平衡问题的电容器调补装置、静止无功发生器(SVG)和复合式换相开关3种解决方案;罗安等[4]分析比较了用于谐波治理问题的无源电力滤波器(PPF)、有源滤波器(APF)和混合型滤波器(HAPF)等设备;郭上华等[5-6]则分别给出了多种改善电压波动与闪变的补偿装置。从经济性层面看,例如周作春等[7]提出了事件型PQ治理方案动态电压调节器(DVR)和不间断电源(UPS)的经济性评估;雷林绪等[8]分析了4种常用的PQ治理方案的经济性评估方法(投资回收期法、净现值法、内部收益率法和全寿命周期成本分析法)。但上述文献所描述的PQ治理方案研究,都是针对某一或几个PQ指标偏差所进行的单次治理过程,对于各种PQ特性各异的不同电网中如何兼顾成本和效益的PQ治理方案优化选择和配置无法提供充分支持。模糊专家系统是第二代专家系统,能够利用人类的专家知识和模糊推理机制,提高决策支持系统的逻辑推理能力,解决具有模糊的、不确定性的和复杂的决策难题。因此,提出一种基于模糊专家系统的PQ治理决策支持系统,旨在综合考虑技术和经济性两个层面,针对目标电网个性化的PQ问题,为用户选择成本效益最优化的PQ治理方案提供辅助决策支持。依据采集到的目标电网PQ指标偏差进行PQ经济损失分析和PQ治理成本分析(可存在多种可选方案)。以所得PQ指标偏差变量和成本效益差值变量为输入,基于所构建的PQ治理决策模糊专家系统进行模糊推理、计算,输出成本效益最优化的PQ治理方案。以目标电网中同时并存三相不平衡和谐波偏差为例,进行了算例分析。
1 系统总体设计分析
由于不同电网PQ特性各异,一方面,如何优化配置PQ治理方案需专家根据其丰富的治理经验进行复杂的建模仿真和计算分析实现。另一方面,若系统已配置多种类型PQ治理设备,当电网中每次发生不同PQ扰动时,如何选择最优方案投入治理都得重新进行判断与分析,增加系统工作负担。为此,构建了一种基于模糊专家系统的PQ治理决策支持系统。
本系统主要有3个核心模块组成:PQ经济损失分析模块、PQ治理方案成本分析模块和模糊专家决策支持系统的建模与实现模块。系统具体组成部分如图1所示。

图1 PQ治理决策支持系统组成Fig.1 System composition of decision support system for power quality control
1) PQ经济损失分析模块。主要用于计算电网中发生PQ指标偏差所造成的经济损失,采用质量损失函数将PQ指标偏差的影响以更直观的货币形式表现出来,可等效视作当PQ治理完成后,系统获得的治理效益。
2) PQ治理成本分析模块。主要用于电网中发生某一种或多种PQ指标偏差时,当选择相应的多种治理方案且治理效益相同(均可有效治理)的情况下,各种治理方案间成本的比较,采用成本效益分析法中的净现值方法实现。
3) 模糊专家决策支持系统的构建与实现模块。系统核心部分,在获取系统电能质量偏差指标数据、PQ经济损失的模糊输入和治理设备成本的模糊化输入的基础上,基于构建的模糊专家系统,经过模糊推理、规则匹配、推理合成、去模糊化等过程,以系统输出的形式得到目标电网的最优PQ治理方案辅助决策。
2 PQ经济损失与治理成本
2.1 基于质量损失函数的PQ损失分析
2.1.1 质量损失函数
根据质量损失理论核心思想,针对有效度量因不同PQ指标[9-10]偏差所造成的损失,提出质量损失函数[11]概念,以实现量化质量特性偏离理想目标值而造成经济损失的目的,其一般形式为
L(x)=K·F(x-H)
(1)
式中:x为质量特性值;H为质量目标值;F(·)为描述质量特性与目标值偏离的函数表达式;K为该偏离所造成的最大损失值。由于x的随机性,L(x)为随机变量,其期望值E[L(x)]可表征产品的经济损失水平。
考虑到二次损失函数缺乏敏感度可调特性,PQ质量损失特性研究中采用具有正态分布特性的概率密度函数构造逆正态质量损失函数,其形式为
(2)
式中σ2为敏感性参数。如图2所示,在其取值不同情况下,该逆正态质量损失函数与二次损失函数的特性比较,具有损失值L(x)不超过最大损失值K、敏感参数σ2可调以及符合PQ经济损失的变化状态等特性。
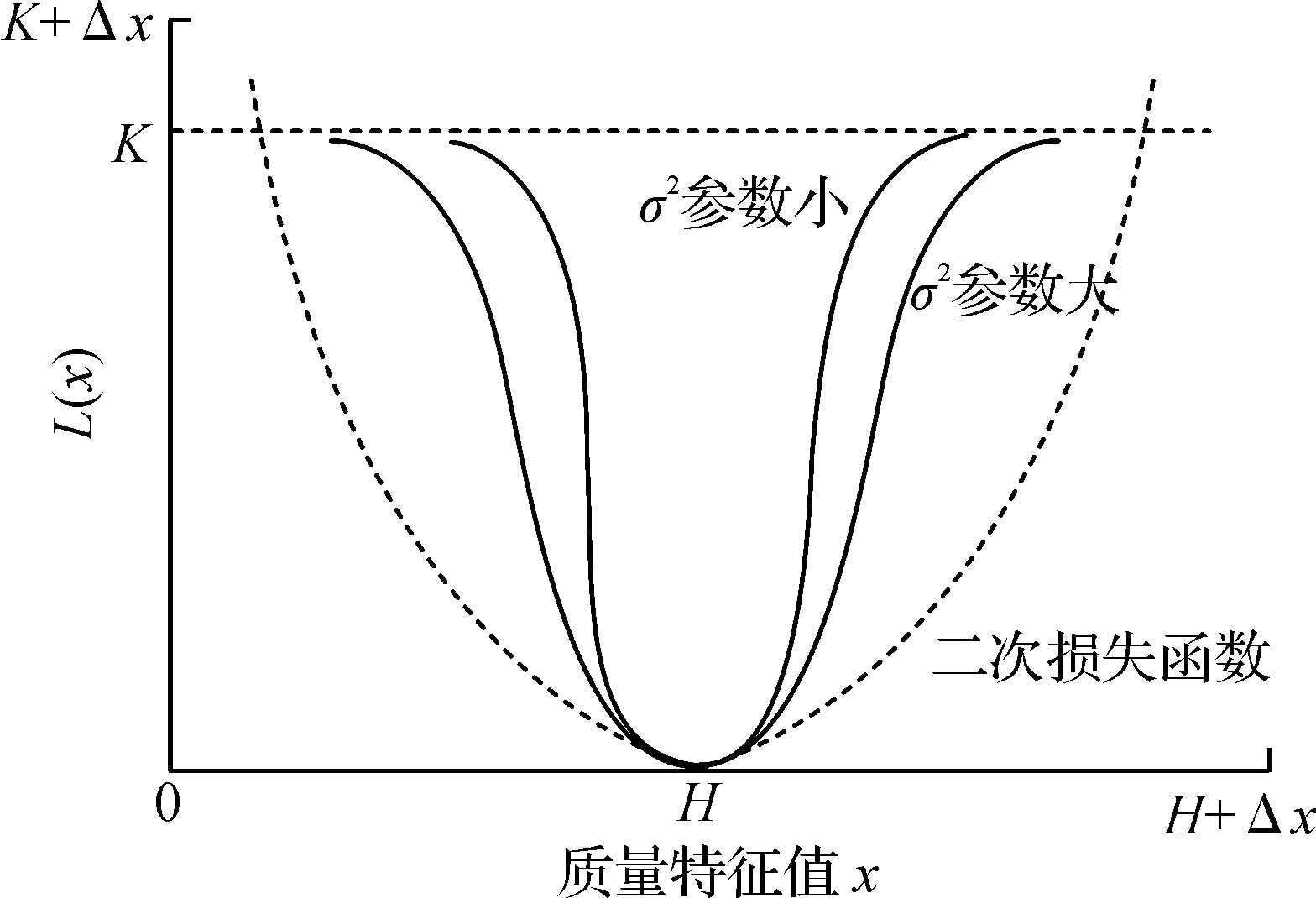
图2 逆正态质量与二次损失函数曲线Fig.2 Loss curves of inverted normal mass and quadratic
由图2可见:选择逆正态质量损失函数具有以下优势:1) 逆概率函数具有最大值,满足质量损失的实际情况;2) 实际系统负荷组成、不同PQ指标损失特性差异很大,逆概率函数拥有良好的敏感参数调节特性,可通过实测数据进行确定,以适用不同场景;3) 逆概率函数特性符合“PQ指标在理想值附近偏差对经济损失影响更大,在远离理想值区域对经济损失敏感度减弱”这一实际情况。
2.1.2 基于质量损失函数的PQ损失分析
连续型PQ指标(包括电压偏差、频率偏差、电压不平衡、电力谐波和电压波动与闪变等)反映的是电压、电流的实际波形与期望波形的差异程度[12],其往往通过波形的偏离程度以及偏离的持续时间来表征。据此特点,基于式(2)可构建适用于连续型PQ损失分析的量化函数为

(3)

基于此,连续型PQ损失分析的步骤可概括为
步骤1根据国家标准[13]和实际需求,将待评估PQ指标进行等级划分。例如,对于10 kV供电系统,如仅按照“合格”和“不合格”两个质量等级考量,连续型PQ指标可按表1所列区间进行简单划分。
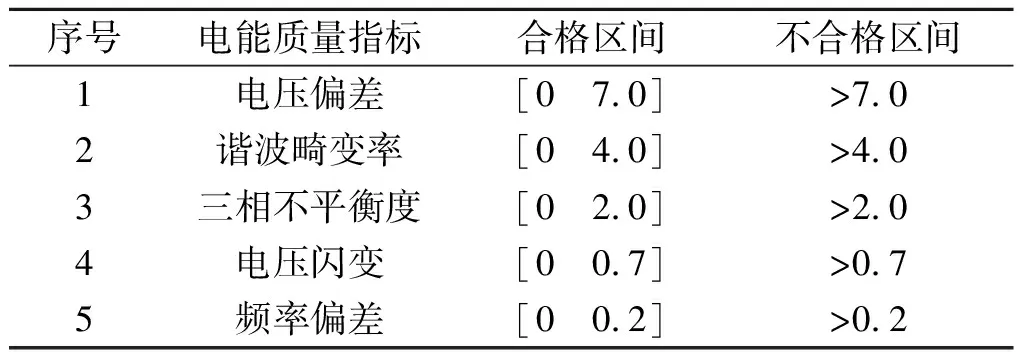
表1 连续型PQ指标的区间划分Table 1 Interval division of continuous PQ indexes %

(4)

步骤4统计该PQ指标在各质量等级下的平均偏离程度及其偏离持续时间之和。设观测期内该PQ指标有n个数据值处于质量等级i下,则
(5)
式中:xij为观测期内该PQ指标在质量等级i下第j个数据值;τij为第j个数据值在质量等级i下对应的持续时间。
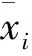
2.2 电能质量治理成本效益分析
为直观、清晰地评估当一个PQ治理方案实施后带来的电网经济得失,可在PQ治理方案成本效益分析中引入现金流量概念。根据现金流量分析理论,将每一个PQ治理方案的投资以及实施后所带来的一系列货币支出视为系统现金流出;而因实行该方案以改善PQ所带来的一切经济效益则为系统现金流入。综合考察现金流量的3要素(大小、方向和时点),现金流入为正,流出为负,两者代数和即为净现金流量。将每年的净现金流量进行累计,即可获得该PQ治理方案的经济效益值。
对于PQ治理方案而言,其设备一般均具有较长的使用年限。因此,方案的成本并非简单地累计初始投资成本加上后续成本要素×使用年限之和,其效益也并非简单地等于每年所减少的PQ损失×使用年限。为更好地评估PQ治理方案的成本效益,需选择合适的经济评估方法,以保证评估结果的准确性。
根据投资决策经济学理论,常用的经济评估方法[14-16]主要有净现值法NPV、内部收益率法IRR和年值法AW。针对这3种方法进行综合比较:由于不同PQ治理方案的内部收益率一般都是不同的,故不宜采用IRR法;NPV法和AW法本质一致,仅表达式不同,前者算法相对简单;工程经济分析也表明,作为投资决策的基础,NPV法最合适。因此,选择净现值法作为PQ治理成本计算依据。
根据PQ治理方案成本和效益的概念定义,净现值CNPV的计算式可表达为
(6)
式中:CI为设备的初始投资成本;Cb为治理方案的年效益值;Ca为治理设备的年使用维护成本;r为贴现率;N为使用年限。
3 PQ治理决策支持模糊专家系统
3.1 隶属函数设置
模糊专家系统采用模糊技术[17]进行不确定性输入处理,基于其实现的PQ治理决策支持系统,可使一般工作人员通过简单的输入操作,获得最优PQ治理方案。利用模糊隶属函数,将输入量经过模糊生成器模糊化后生成模糊变量(即参数语言变量)。为了专家知识表达的便捷性和计算过程的简化性,拟采用梯形函数形式的模糊隶属函数[18]。
根据系统需求,定义模糊专家系统的输入变量为各个PQ指标偏差值:Dvol(电压偏差值)、Dhar(谐波偏差值)、Dunbal(三相不平衡偏差值)、Dflu(电压波动与闪变偏差值)、Dsci(短路电流水平)。前4个变量的参数采用Delt(持续时间久)和Dest(持续时间短)两个等级划分,Dsci变量参数采用DL(水平低)和DH(水平高)两个等级[19]划分。以Dhar和Dsci变量参数为例,其隶属函数分布如图3所示。

图3 Dhar和Dsci偏差值隶属函数分布Fig.3 Membership functions of Dhar and Dsci
图3(a)中横坐标表示Dhar在整个观测时间存在的持续时间论域值,100是指将数据的观测时间归化分成一百份的结果,纵坐标表示存在时间的模糊化结果(即得到其隶属函数值)。图3(b)表征观测期间系统中出现Dsci的数值大小,横坐标表示Dsci的论域值,1 000是根据电网规格、容量等特征确定的衡量电网短路电流水平的最大值,纵坐标也是其隶属度函数值,表示Dsci值的模糊化输入。
模糊专家系统的另外两个输入变量是PQ治理经济损失与成本分析的结果值。考虑到谐波和无功功率是实际电网中最常见的两类PQ问题,且其治理原理及方案区别较大(无功治理主要针对电压偏差、三相不平衡和电压闪变指标;谐波治理主要针对谐波指标),系统规划针对这两种PQ问题进行求解。如图4所示,这两类PQ指标项的不同治理方案对应不同的成本效益分析隶属函数,其输入变量分别定义为Crea(无功成本效益比较)和Char(谐波成本效益比较)。
图4表示针对某一个或多个指标发生偏差时,对应的两种治理方案的成本效益分析值比较(理论上解决方案可有更多种)。数值横坐标的论域范围值是基于相关设备成本等参数值调研的合理假设,

图4 PQ治理设备成本效益分析隶属函数Fig.4 Membership functions of Crea and Char
使用时可按照系统实际需求作适当修正.2万元是考虑在市场上,当一个设备的价格优于另一个设备时,所自行设定的考虑阈值,即超过2万元,会选择相比较便宜的设备,当然这只是一种假设,在实际的应用情况中,可根据具体情况更改数值的大小,但该变化特性是不会改变的。图4(a)中共有3组梯形线段组(a-1,b-2,c-3),图4(b)中共有2组梯形线段组(a-1,b-2),其设定依据是通过查阅、参考相关治理设备的成本和使用年限等参数,统计分析在相同容量范围下不同PQ指标偏差治理设备的成本效益差异情况,每组梯形直线的区别在于不同PQ指标所造成的损失与治理设备成本类别的不同,其具体差异数值可根据具体使用情况做适量调整。以图4(a)中线段组a-1为例进行说明,a:C(capacitor-condenser<0)表示在同一个PQ问题背景下,配
置电容器(capacitor)的成本效益值小于配置调相机(condenser),基于经济性考虑模糊专家系统应该输出配置调相机治理方案;1:C(capacitor-condenser>0)表征的意义与a线段恰相反,即配置调相机的成本效益值低于配置电容器,决策支持系统应输出配置电容器的治理方案。
根据输入变量的不同特性,对应两种模糊决策器的输出变量也可分为两种类型。第1种是无功治理(Erea)设备,所采用输出参数是可以进行无功治理的备选设备名称,包括APF,SVC,DVR,condenser,capacitor,wxzl(无需治理);第2种是谐波治理(Ehar)设备,所采用输出参数是可以进行谐波治理的备选设备名称,包括wxzl,PPF,APF,HAPF。两种输出变量的隶属函数分布如图5所示。

图5 两种输出变量的隶属函数分布Fig.5 Membership functions of Erea and Ehar
图5中各三角形隶属函数表征各PQ治理设备在模糊专家系统中的模糊输出值,是根据治理设备的种类汇总来决定的,每一个三角形代表一种治理设备。两个三角形叠加区域表示在该输出值范围内对应两种治理设备均可由推理得到,但最后输出的推荐治理设备由隶属度高者确定。例如,当Erea变量输出值为2.6时,从图5中可看到:SVC和DVR设备均可被推理得出,但由于DVR对应隶属函数值大于SVC,最后输出应为DVR治理方案。
3.2 规则库的建立
基于上述输入、输出变量的隶属函数确定知识表达形式,进行知识的获取与表示,并采用产生式规则有效确立模糊推理专家系统的知识规则库。本决策支持系统设计的思路,电网中发生PQ指标偏差时系统提供的选择候选治理方案在实践中均被证明是可行的,因此,主要考虑其成本效益,使得系统治理效果与成本效益取得平衡优化。根据规划需要,系统规则库共制定了41条模糊推理规则,包括0~2个PQ不同指标发生偏差场景时的PQ治理方案决策规则。下面进行规则解读:
规则1“ifDvolisDeltandDharisDestandDunbalisDestandDsciisDLandDfluisDestandCreaisC(capacitor-condenser>0)andCharis none, thenEreais capacitor,Eharis wxzl”。
规则2“ifDvolisDeltandDharisDestandDunbalisDestandDsciisDLandDfluisDestandCreaisC(capacitor-condenser<0)andCharis none, thenEreais condenser ,Eharis wxzl ”。
规则1解释:如果Dvol(电压偏差值)时间是持久的,其他指标的偏差时间是较短或可忽略的,考虑到电压偏差的候选治理设备调相机和电容器的Crea结果为C(capacitor-condenser>0),说明投电容器比投调相机设备经济,因此系统输出的无功治理设备优选方案为电容器。规则2解释:同样场景下,若根据Crea计算得到C(capacitor-condenser<0),说明投调相机比投电容器设备经济,可得到无功治理的输出变量设备应为调相机。规则1,2中,由于谐波偏差均已忽略(DharisDest),因此谐波治理输出变量都为“无需治理”。
3.3 模糊推理的实现
采用合成推理实现模糊专家系统中的模糊推理,其基本思想是:先求出规则“ifX1ism,X2isp,X3isq,X4isd,X5ise,X6isf,X7isg,THENY1isw,Y2isu”中模糊集合{m,p,…,g}和模糊集合{w,u}的模糊关系R,然后将R与输入事实“X1ism1,X2isp1,X3isq1,X4isd1,X5ise1,X6isf1,X7isg1”进行合成运算,得到系统的模糊输出变量。
采用Mamdani构造实现模糊关系R的构造[20],定义R为
μR(x1,…,x7,y1,y2)=μm(x1)∧…∧
μg(x7)∧μw(y1)∧μu(y2)
(7)
式中:∧代表取小;μm(x1)为论域上的模糊集m的隶属函数;x1为论域X1上的元素;μR(x1,…,x7,y1,y2)表示R的隶属函数。
采用极大-极小合成运算方法作为R与模糊集合{m1,p1,…,g1}的合成运算方法,其表达式为
(8)
式中:∨表示取大;μw1(y1),μu1(y2)分别为最终输出论域Y1,Y2上的模糊集合w1,u1的隶属函数。
对于PQ治理决策支持专家系统,其输出治理设备应是一个清晰值,因此最后需将所得模糊输出变量进行去模糊化操作。考虑输出隶属度函数的形状需求,本系统采用重心法[21]实现去模糊化,即取模糊隶属度函数曲线与横坐标所围成面积的重心为模糊推理的最终输出值。其公式为
(9)
式中:y1表示论域Y1上的元素;W,U分别为模糊集合w1和u1上的清晰值,即PQ治理决策模糊专家系统最后给出的最优PQ治理设备。
本系统的模糊推理过程核心步骤如下:
1) 录入事实。记录下PQ指标在一段观测时间T内发生偏差的存在时间占比,进行输入变量模糊化操作,得到相应指标(Dvol,Dhar,Dunbal,Dflu,Dsci)的模糊输入隶属函数变量;当指标存在时间占比大于30%T,即隶属输入为Delt;否则为Dest;接下来计算相应治理设备的成本效益值(Crea,Char),将上述两部分输入变量作为系统输入变量录入。
2) 规则匹配。为提高匹配的效率,在知识库中采用RETE匹配算法对系统中的41条规则与录入的事实(即步骤1)的输入变量)循环进行模糊匹配,判断在规则库中有无可匹配规则,即是否有规则的事实部分与录入事实描述的相符或部分相符,若有则跳入下一步,否则跳转到步骤4)。
3) 冲突消解。若规则库有多条规则匹配成功造成事实冲突,即当PQ指标有一个或多个偏差的规则都与录入事实满足模糊关系时,会激活相应的多条规则,则按照冲突消解策略消除冲突,然后跳转到步骤5)。
4) 输出结果_1。规则库中无匹配规则,输出无解,即此电网指标偏差情况,规则库无录入,可将此条事实作为一条新的规则,输入系统中,并为其配置相应的备选治理设备方案,结束推理过程。
5) 输出结果_2。得到匹配规则,执行匹配规则的动作部分,得到输出变量,即得到最佳治理设备,结束推理过程。
4 案例分析
基于Matlab/Simulink软件中SimPowerSystem模型库构建IEEE 13节点的配电网仿真模型,线路参数详见文献[22],电压等级和负载容量分别设定为10 kV,10 000 kVA。为使获得的PQ数据具有变化特性,仿真模型中各节点负荷均设置为具有波动特性的负荷变化曲线。设在1天24 h的观察时间窗口内,以30 min为观察时段,随机间隔记录各时段PQ指标数据。经分析,电网中同时存在谐波问题和三相不平衡指标偏差问题,需要进行治理改善。其中三相不平衡度偏差限值为2%,谐波畸变率偏差限值为4%。具体数据如表2所示,表2中T1~T10表示所取10次观察时段,并以这些时段内所记录的PQ数据为代表,作为案例分析的样本数据。
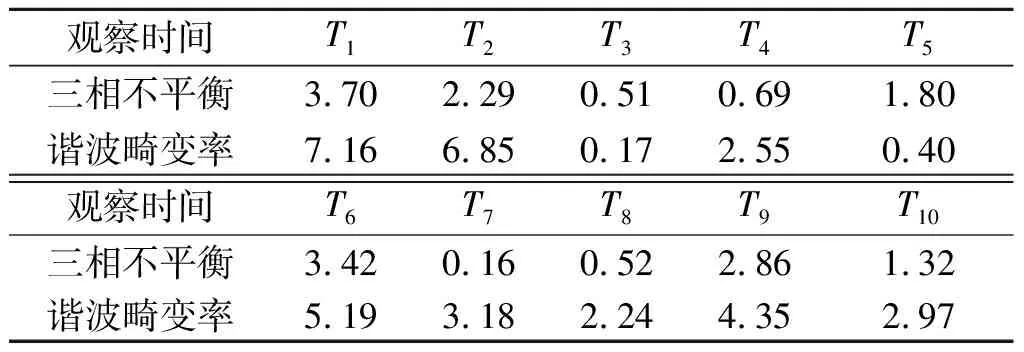
表2 观察时段PQ指标运行数据Table 2 PQ indexes data in observational periods %
首先,根据第2节所述的PQ经济损失分析方法进行质量损失计算,步骤如下:
步骤1查阅表1,可得针对三相不平衡指标的区间划分:0%~2.0%为合格区间不会产生经济损
失,>2.0%将会产生经济损失;针对谐波指标:0~4.0%为合格区间不会产生经济损失,>4.0%将会产生经济损失。
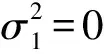
步骤3将步骤2计算所得各指标参数代入式(3),可分别得到三相不平衡和谐波指标偏差的质量损失函数的公式为
(10)
根据式(10),可分别绘制出该配电网电压不平衡度、谐波偏差与经济损失评估值之间的关系,如图6所示。由图6可见:随着PQ指标偏差值及偏差存在时间的增大,由此造成的目标电网经济损失评估值将快速增加(但应受限于图2中所示的最大损失值K)。

图6 PQ指标偏差与经济损失值关系Fig.6 Relations of economic losses and PQ deviations

接着,根据系统存在PQ问题,进行PQ治理设备的成本效益分析:
1) 选择治理设备。针对三相不平衡,由于DVR可以根据网侧电压的需要,改变其发出的波形,使供电电压恢复到三相平衡状态,保障用户端的供电质量,而SVC可以通过控制与电抗器或电容器串联的晶闸管导通角来调节系统无功功率输出,达到控制系统三相平衡的目的,因此预先设定两种DVR和SVC有效治理设备作为备选方案;针对谐波问题,由于PPF不仅可以吸收谐波电流,同时还可以进行无功功率补偿,运行维护也简单,而APF可以有效地起到补偿或隔离谐波的作用,因此预先设定PPF和APF两种有效治理设备作为备选方案,进行成本分析。
2) 治理成本计算。查阅相关资料及考虑本次案例实际情况,合理设定由谐波、三相不平衡所引起的偏差的补偿容量为其最大功耗的1.25倍,同时在参考了各候选设备的市场成本情况下,确定其相应容量的市场购买成本,取10%购买成本为后继维护成本,可得治理设备成本即是前期投入的市场设备购买成本加上后期的设备维护成本,结果如表3所示。

表3 各设备的成本参数Table 3 Cost parameters for equipment
3) 成本效益值的计算。将前面计算得到的PQ经济损失值和治理成本都折算为使用年限15年,贴现率r为10%。如DVR的效益值折算为27.3万元。采用净现值法,根据式(6)即可得到治理设备的成本效益值,通过计算可得结果(表4)。基于此,可以得到模糊专家系统的两个关键输入变量Crea的数值为-11.1万元,隶属函数为C(DVR-SVC<0),Char的数值为11万元,隶属函数为C(PPF-APF>0)。

表4 各种设备净现值比较Table 4 Comparison of NPV of various equipment
由于在观察时段内,三相不平衡指标和谐波指标偏差的持续占时比均为100%,因此输入指标分别为Dhar,Dunbal为100,其余Dvol,Dflu,Dsci为0。将这些变量值均输入已构建模糊专家系统的综合数据库,配合规则库中的41条模糊推理规则,基于模糊推理机进行有效推理,并将推理结果进行去模糊化处理,最后PQ治理决策模糊专家系统的输出结果如图7所示。

图7 模糊专家系统输出结果Fig.7 Output results of fuzzy expert system
由图7(a,b)分别可见:当隶属函数为1时,输出变量Erea=2,Ehar=1。查阅图5所示的输出变量相关隶属函数,可知决策支持系统最终选出SVC和PPF这两种设备作为目标配电网的三相不平衡和谐波问题治理方案。因为SVC与DVR相比,尽管从技术角度考虑两者均可以实现目标电网三相不平衡问题的有效治理,但从经济性角度考虑,在获得效益一定的水平下,SVC相比DVR所投入的成本更小(设选择SVC和DVR两种方案进行治理,将成本效益均折算为15年,使用SVC方案最终比使用DVR方案多实现盈余11.1万元)。同理,为实现目标电网谐波问题,PPF和APF两种备选方案中,选择PPF比APF将多实现盈余11万元。因此,在PQ治理效果相近情况下,为实现效益最大化,辅助决策专家系统推荐SVC和PPF这两种PQ治理方案。周作春等[7]以DVR和UPS为例,详细分析了两种设备治理方案成本计算,在一定程度上忽略了效益方面不同,同时考虑PQ指标偏差的效益与治理设备成本的计算,给出了详细的计算过程,结果更令人信服。杨振宇等[16]使用了成本效益分析方法,同时考虑了PQ指标偏差的经济损失与治理设备的成本分析,得到推荐的治理方案,此过程是人工收集数据并进行相应的计算过程,每发生一次故障,都得重复作业1次,人工操作与时间利用不够有效。本例采用的基于模糊专家系统的决策支持系统可以通过对构建的专家系统进行简单的输入操作,自动完成推荐治理方案的过程,实现速度快,得到的结果精度更高。
5 结 论
构建的基于模糊专家系统的PQ治理方案决策支持系统适用于PQ特性各异的不同目标电网进行PQ治理方案的优化推荐选择。系统推理时,需将系统PQ指标偏差数值,以及PQ治理成本和效益均作为有效输入进行综合考虑,本决策专家系统所推荐的PQ治理方案同时兼顾了技术有效性和成本经济性。需说明的是,所构建的决策支持模糊专家系统仅为初级模型,其中所含的PQ指标种类与治理效果的等级划分均不够完全,可选择的治理设备也不够全面,尚不能完全满足实际配电网中复杂PQ问题发生时的PQ治理方案优选需要。针对这些问题,后继还需展开深入研究以期完善,使其具有更好的工程应用价值。
