基于Mixture模型对翼形空化的数值模拟

肖鑫明，桂 林

(四川大学水利水电学院，成都 610065)

0 引 言

在水力机械中翼形空化是由于水流绕流叶片引起压力降低而产生的[1]，当流场中某点的压力低于液体介质工作温度所对应的汽化压力时，该处液体发生相变，产生气泡，气泡生长直至溃灭的现象即为空化现象[2]。当溃灭发生在水力机械固体表面附近时，流体中连续破灭的空泡所产生的高压力不断作用于固体表面，会造成流体机械表面的损坏，并兼有振动、噪声及性能下降等现象[3]。叶片的进口处截面便是一个简单翼形，可以通过研究翼形来研究这种汽蚀性能的变化。于凤荣等人通过在翼形上打孔作了相关研究，利用单相模型证实了打孔可以破坏翼形上方区的低压流场[4]。王鑫等人进一步对孔的布置方式和位置、孔的数量和深度等参数对翼形的影响进行了具体研究[5]。戴月进等人研究了翼形表面粗糙带对空化效果的抑制[6]。2018年李雅琴等人利用Mixture多相流模型模拟了二维翼形的空化情况[7]。但以上翼形空化的研究要么限于单相流的研究，要么仅仅是利用多相流模型进行初步的模拟，随着CFD技术的不断发展，现在的多相流模型已能达到足够的精度来胜任进一步的模拟，本文将基于Mixture模型对微孔及翼形表面粗糙度对三维翼形的空化影响作进一步的探究。

1 翼形流动特性

1.1 微孔和翼形表面粗糙度影响空化原理

微孔改善翼形性能，主要是因为翼形表面微孔提前将固体表面的层流边界层转换为湍流边界层，后者有更好的附着性，从而推迟了固体表面边界层的脱落与分离，减小了翼形后漩涡区的面积与强度，大幅降低了翼形的压差阻力[5]。而在翼形表面施加粗糙带可有效增加翼形表面附近流场的湍动能，改变压力分布，从而影响水翼初生空化的发生[6]。

1.2 升力、阻力特性

翼形升力公式为：

(1)

翼形阻力公式为：

(2)

式中：Cl为升力系数；Cd为阻力系数；ρ为流体密度，kg/m3；v∞为来流速度，m/s；S为翼形平面面积，m2。

在改善翼形空化性能的同时，还要注意翼形的水动力性能，往往我们会通过升阻比这一新的特性系数来确定翼形的升阻性能以及来改善优化它的升力性能[8,9]。升阻比一般用L/D表示，升阻比又称“举阻比”。翼形在运行过程中，在同一迎角的升力与阻力的比值与翼形的迎角、流体的速度等参数有关，此值愈大说明该翼形工作面的水力动力性能愈好[10]。因此在后文比较完几种方案的空化情况后，还会对升阻比进行分析。

2 数值模拟过程

2.1 计算区域与网格划分

(1)模型建立。在Solideworks中导入翼形NACA-0016的数据，翼形长为100 mm，位于一个长方体的流道内，x=0～300,y=-40～40,z=0～240,翼形顶部距离入口80 mm。为了更好地观察升力系数和阻力系数的变化，将翼形的攻角设置为8°，见图1。在微孔试验中还会为翼形低压区添加微孔，孔径为1 mm。为了更好地观察添加微孔后的变化，在y方向上添加等距的3个微孔。

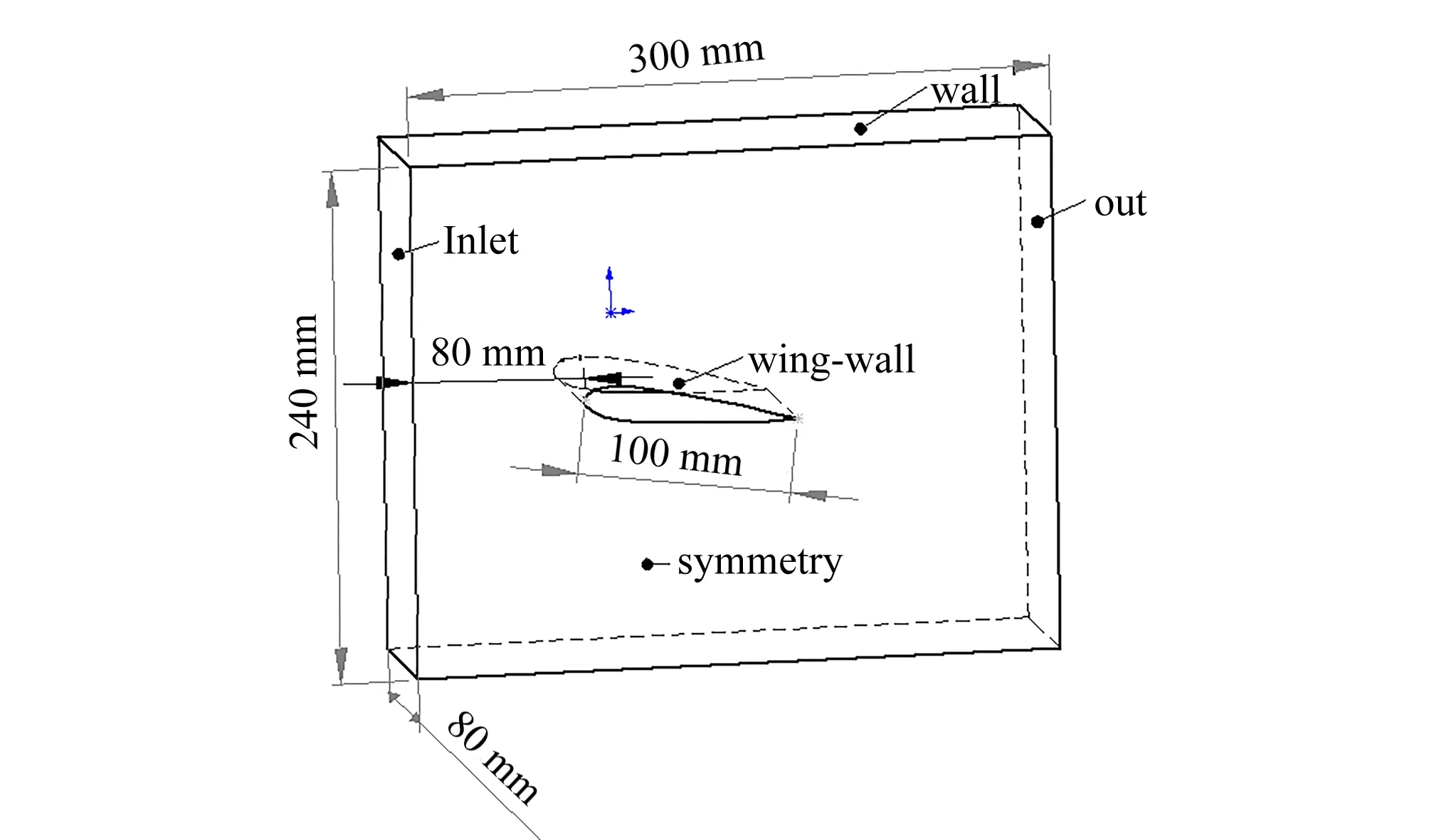
图1 模型尺寸Fig.1 Model size drawing

(2)空化区的确定。图2为数值计算得到的无孔翼形工作面空泡份额分布曲线，可以确定开孔的空化区，选择开孔位置位于距离翼形前缘10 mm的位置进行开孔。

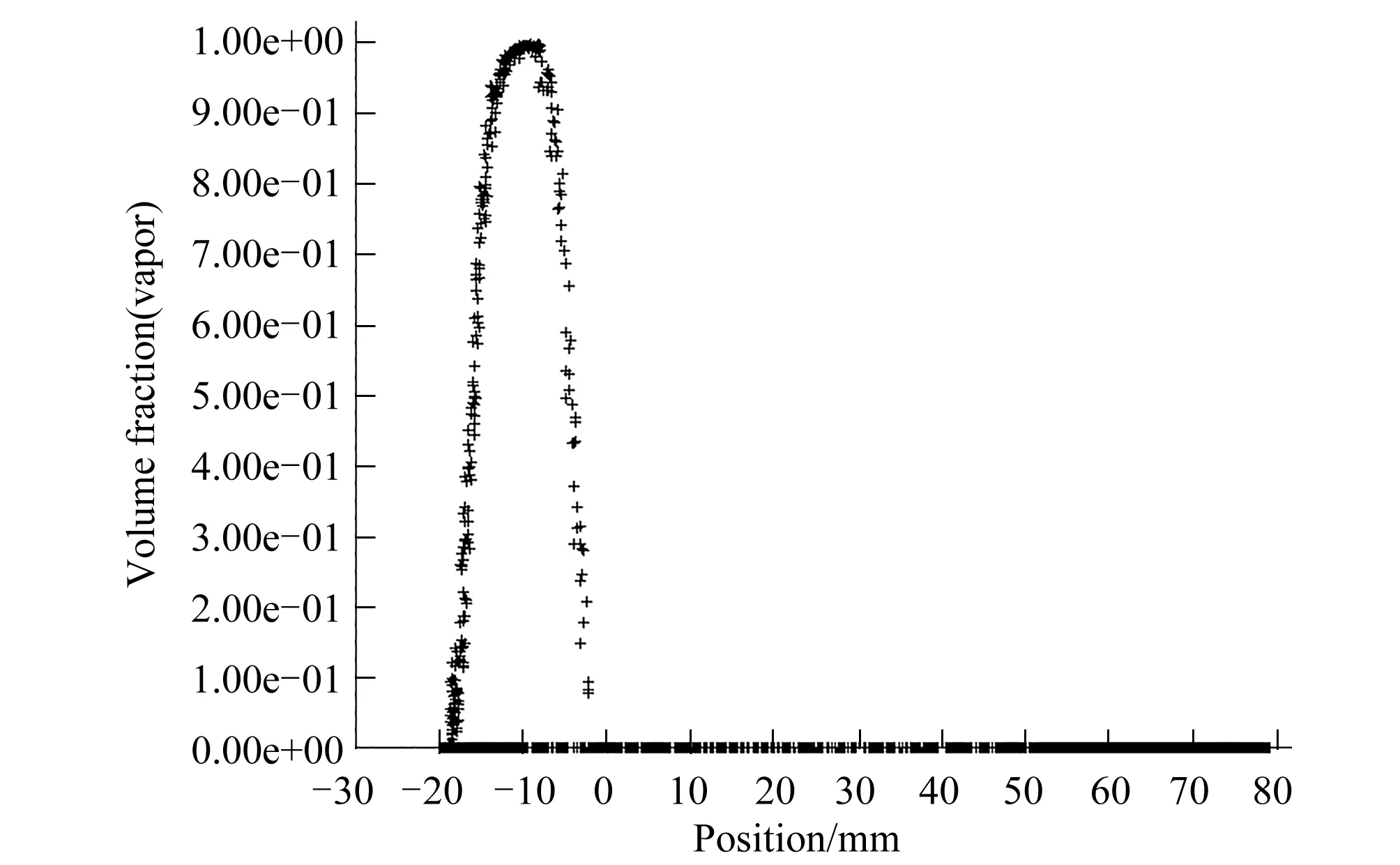
图2 翼形空泡分布曲线Fig.2 Airfoil bubble distribution curve

(3)网格划分。利用ANSYS Meshing软件对模型计算区域采用非结构网格进行划分(见图3、图4)，并在翼形壁面进行边界层网格的划分，且在翼形工作面边界、前缘、后缘都进行加密设置，所得网格数量在100 万个左右。接下来对网格进行疏密的敏感性分析。由于计算机计算能力可较快计算出本模型100 万个网格的结果，故在敏感性分析中只对网格进行再加密至200 万个，所得的翼形空化情况及生升阻力系数的值差别非常细微，但计算收敛时间却增加了3倍左右。平衡计算精度与计算时间，最后选取了网格在100 万个左右的方案。

图3 网格整体划分Fig.3 The overall grid division diagram

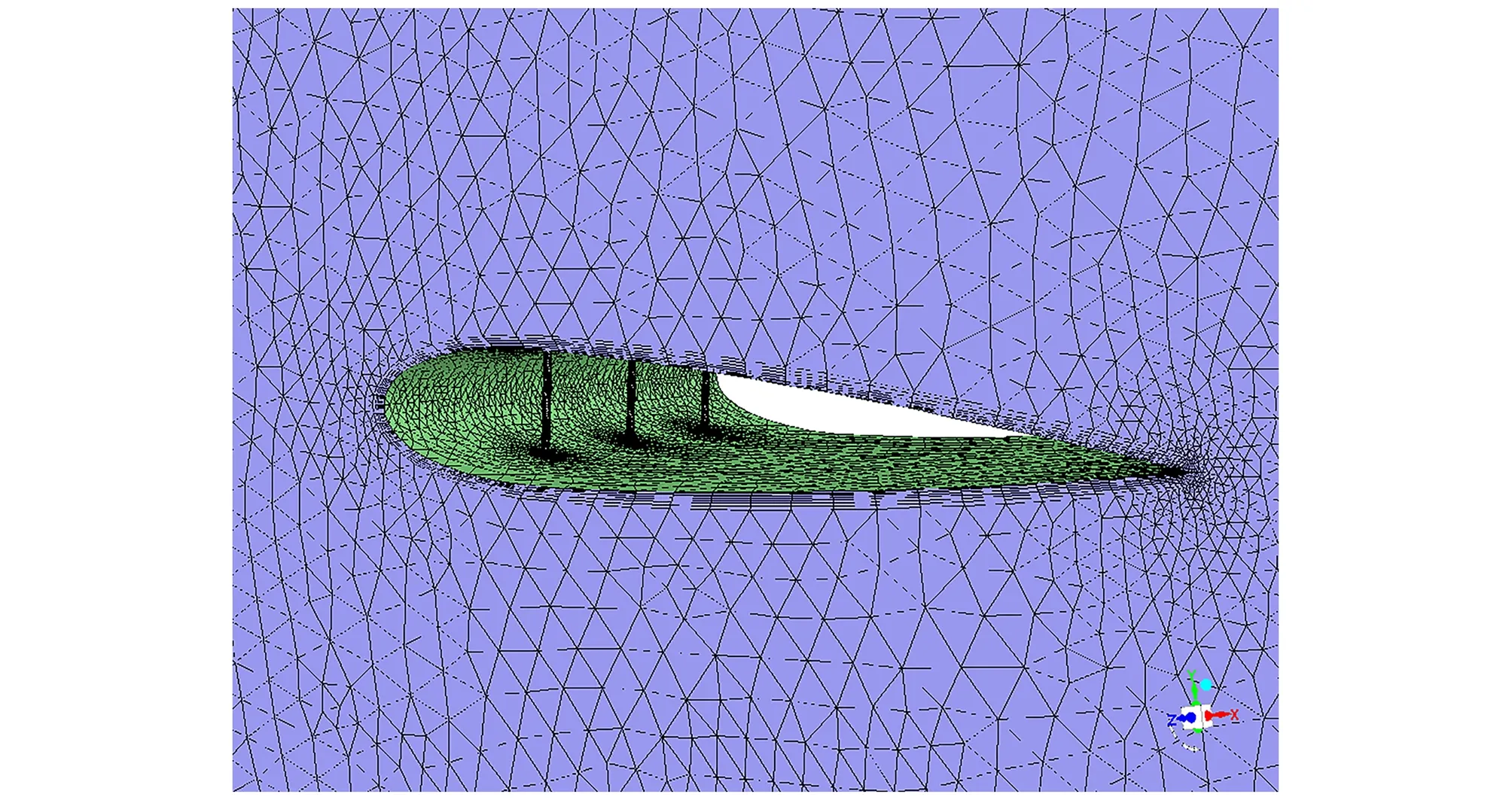
图4 网格细部划分Fig.4 The detail grid division diagram

2.2 湍流模型

SSTk-ε模型是用Menter[11]发展而来的，以便其在广泛的领域中可以优于k-ε模型，而且在带有压力梯度的流动中其计算结果更加准确。占梁梁[12]通过对比几个方程得出从模拟空化状态下翼形能量特性的角度来看，优先选择SST模型较好的结论，故本文的模拟选用SSTk-ε模型。该模型将k-ω模型和k-ε模型以加权平均的方式结合起来，兼具k-ε模型对远场条件依赖性较小和k-ω模型在近壁面模拟准确度较高的特点，方程表达式为：

(3)

(4)

式中:方程右侧的前3项分别为湍流生成项、耗散项和扩散项；ω方程右侧的C项代表交叉扩散项；各常、系数的取值详见文献[13]。

2.3 多相流Mixture模型

该模型是一种简化后的多相流模型，主要用于模拟各相存在不同速度的多相流动计算。由于假定了流动在短空间尺度上局部的平衡，相与相间的耦合是很强的[14]。因此可以应用于模拟存在强烈耦合的各相同性多相流和各相似或相同速度运动的多相流。本文研究选用此模型基于空化两相流来进行数值计算。其主要方程如下。

气相输运方程：

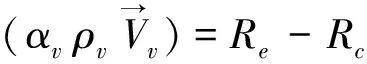
(5)

气泡动力学方程：

(6)

2.4 空化模型

Singhal完全空化模型[15]综合考虑了湍动能以及水中存在的气核的影响，因此得到了广泛的使用。其质量输运方程中2个参数计算方法如下：

P≤Pv

(7)

(8)

式中：Fvap为蒸发系数；Fcond为凝结系数；fv为气相质量分数；fg为不可凝气体质量分数；k为湍动能；Pv为饱和蒸汽压。

2.5 边界条件

使用Fluent软件对三维翼形空化进行数值模拟时，边界条件设置如下:①入口边界条件水的速度设置为10 m/s，空泡份额为0，根据来流条件计算设置湍流强度为5.11%，水力直径为120 mm。②出口边界为了防止回流设置成压力出口，压力大小与大气压一致，空泡份额设置为0，湍流强度和水力直径设置与入口相同。③沿流向两侧边界采用对称边界条件，各变量沿法向的分量为零。④上下两边面及微型孔壁采用无滑移光滑固壁边界条件。⑤翼形四周的壁面在表面粗糙影响试验中采用粗糙高度0.3 mm，其余试验均采用无滑移光滑固壁边界条件。

2.6 离散方法

采用Fluent求解器中基于压力的求解器进行计算，采用Coupled算法实现对压力场和速度场的迭代求解，对压力方程采用Presto格式，其余采用Quick格式进行离散。

2.7 试验方案

本文总共采取4种方案，第1种方案不作任何处理(A方案)，第2种方案给翼形表面添加0.3 mm粗糙高度(B方案)，第3种方案为在翼形空化区开微孔(C方案)，第4种方案在翼形开微孔方案上给翼形表面添加0.3 mm粗糙高度(D方案)。

3 计算结果及分析

3.1 模拟结果的收敛性

按照给定条件对相关参数设置后，分别对4种方案进行模拟计算。由图5的残差监测曲线可以看出，中途出现了几次波动，是由于计算过程为了促进收敛不断调整残差而产生的，结果除Continuity之外其余的残差收敛值皆小于1e-04。判断Continuity是否收敛还可以通过计算进口与出口质量流量差来判断，如果差值小于总流量的0.5%，也可以判定为收敛。由图6可知，差值远小于总流量的0.5%，质量流量达到了稳定值。由此说明通过区域的质量流量是连续的，满足质量守恒定律。

图5 残差监测曲线Fig.5 Residual monitoring curve

图6 质量流量连续性检查Fig.6 Quality flow continuity inspection

3.2 翼形表面压力及空化分布

结合图7的压力分布、图8的速度分布、图9的翼形表面空化分布可以看出，翼形吸力面前段流体速度增大导致这个区域压力降低，当压力下降至饱和蒸汽压之下时，这个局部区域中的水发生相变形成气相空腔，可以看到，先是一部分气相空腔溃灭，再达到一个完全气相空腔溃灭，空化的前段为气液两相混合区，中段充满气相，后半段是气液两相混合区，也就是本文主要研究的翼形空化现象，另外从速度分布图中还可看出在翼形的尾部形成回射流漩涡。

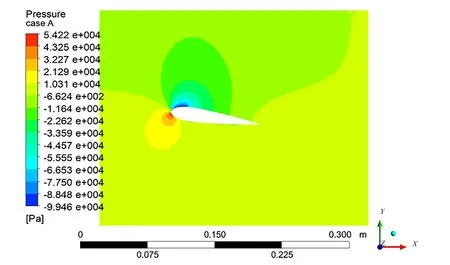
图7 方案A侧面压力分布Fig.7 The lateral pressure distribution of case A

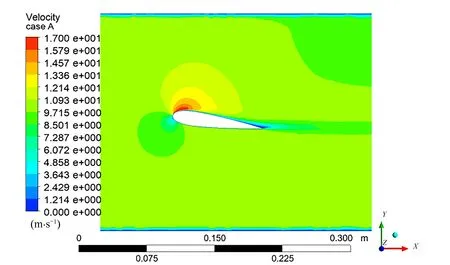
图8 方案A侧面速度分布Fig.8 The lateral velocity distribution of case A

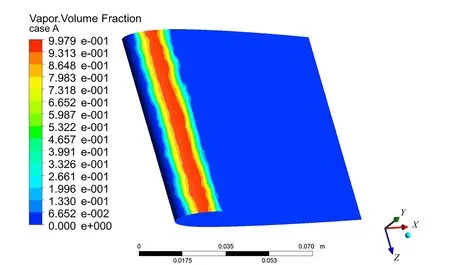
图9 方案A翼形表面空化分布Fig.9 Airfoil surface cavitation distribution of case A

从图8、图9对比图7来看，无论是在翼形表面增加微孔还是增加翼形表面的粗糙程度，均对翼形空化有一定的改善效果，增加翼形表面的粗糙程度可以将整体的空化情况降低，而增加微孔仅可以降低微孔及微孔之后区域的空化情况，这与文献[5]和文献[6]中用单相流模型模拟所得出的结论一致，可以判断多相流模型模拟翼形空化的正确性。从图10可以看出，当在翼形表面增加微孔并且增加翼形表面的粗糙程度时，翼形空化的情况改善得最好。方案B、C、D的翼形表面空化分布分别见图10、图11、图12。

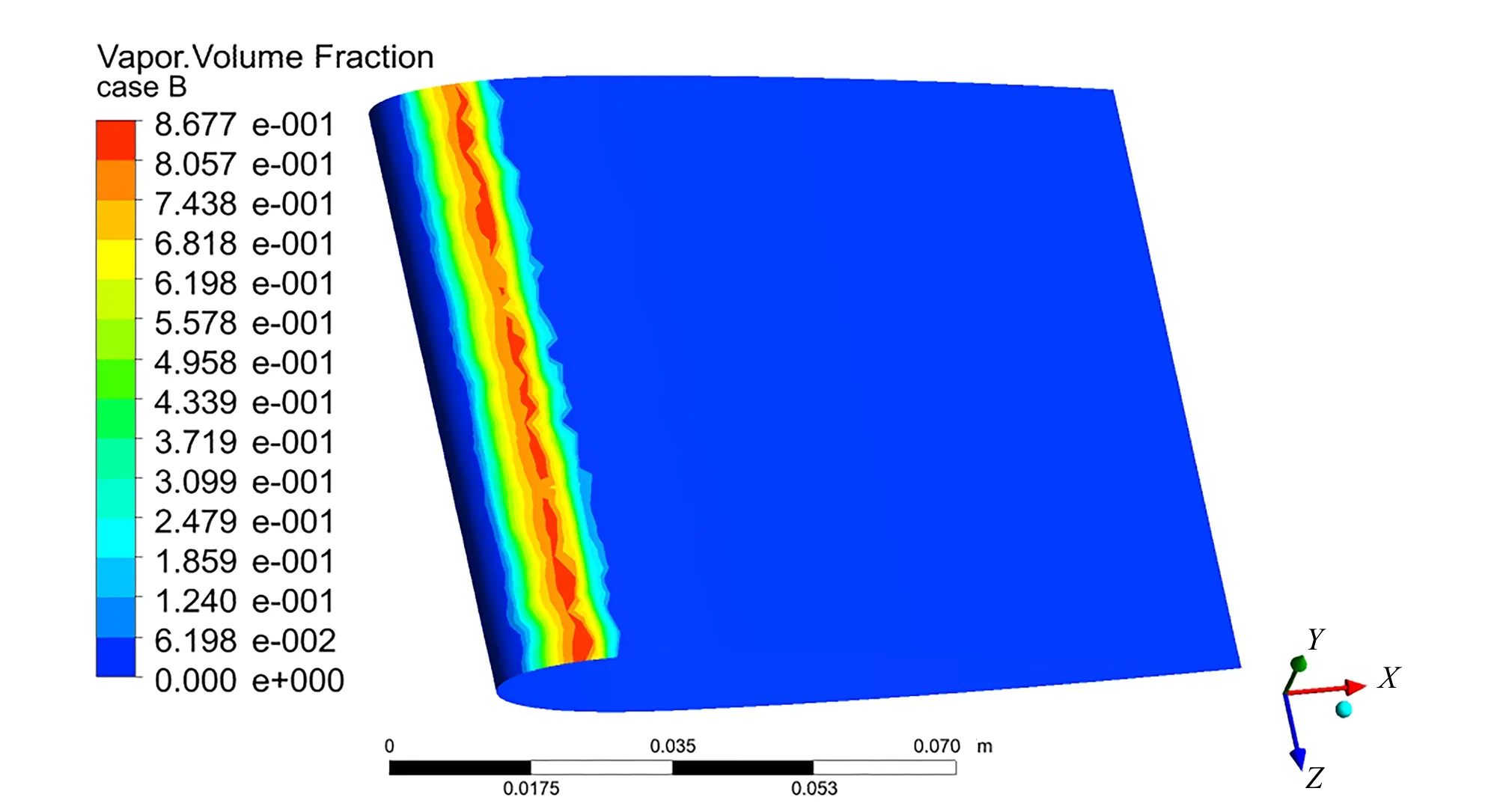
图10 方案B翼形表面空化分布Fig.10 Airfoil surface cavitation distribution of case B

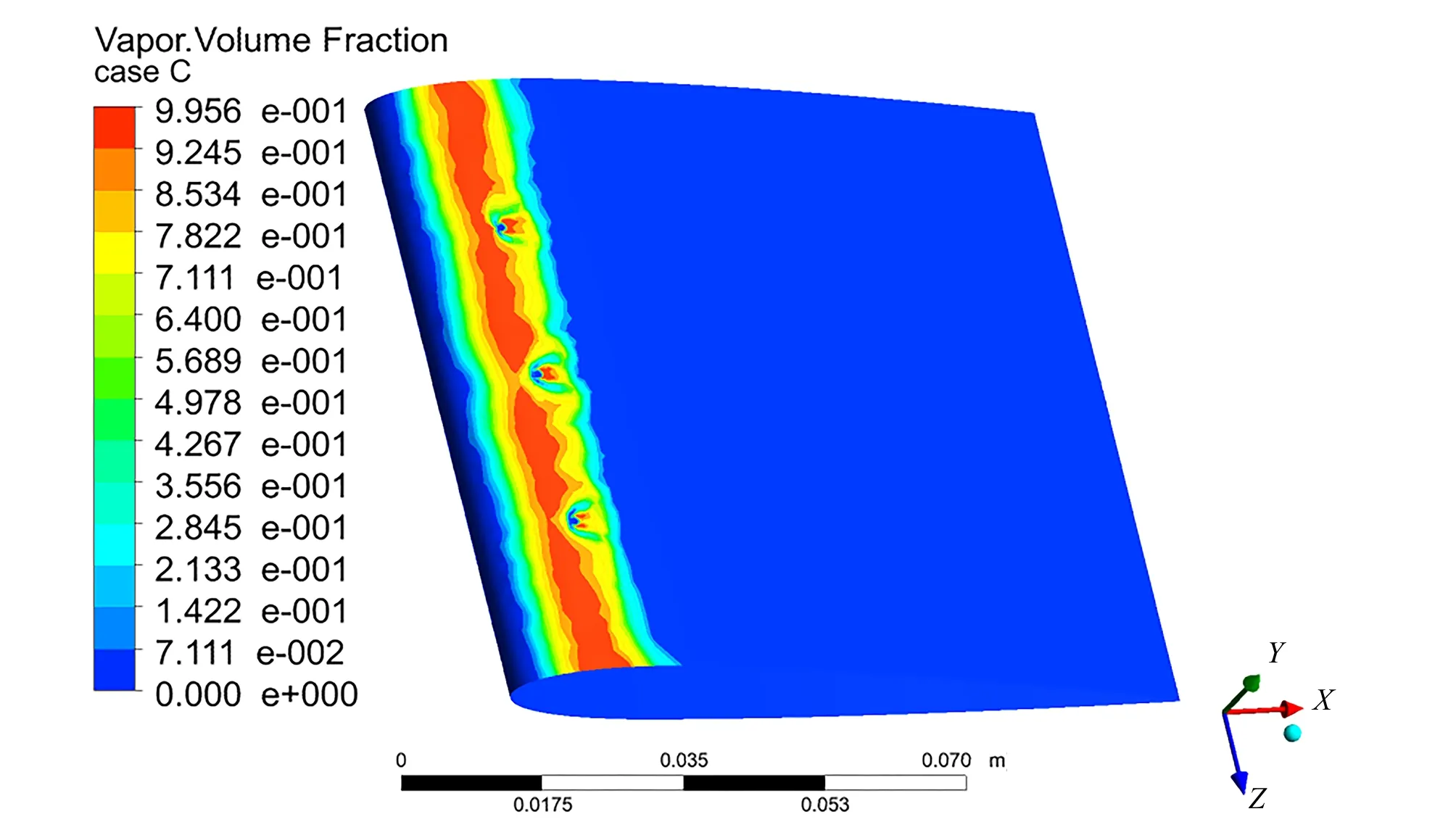
图11 方案C翼形表面空化分布Fig.11 Airfoil surface cavitation distribution of case C

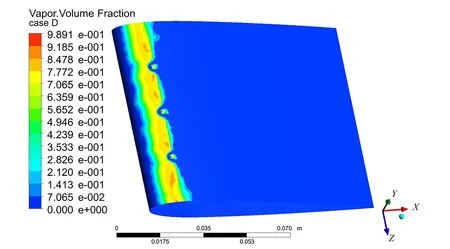
图12 方案D翼形表面空化分布Fig.12 Airfoil surface cavitation distribution of case D

3.3 3种情况对水力特性的影响

通过表1和图13可以看出，方案B增加了翼形表面粗糙度后，翼形的升力系数减少了7%左右，阻力系数增加了5%左右，升阻比下降11%左右。增加微孔方案C在升力系数和阻力系数上均与未增加微孔和表面粗糙度的方案A持平。方案D表明增加微孔在一定程度上提升了仅增加表面粗糙度的升力系数，但同时也增加了阻力系数，导致最后升阻比和方案B基本一致。基于以上的对比可知，增加微孔对翼形的主要水力特性升阻力基本不会造成什么影响，而增加翼形表面的粗糙度会对翼形的主要水力特性升阻力造成一定的削弱影响。

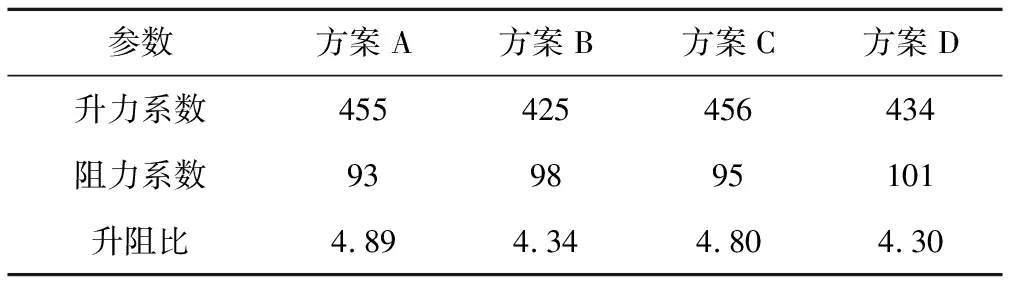
表1 翼形表面升阻力系数对比Tab.1 Comparison table of lift drag coefficient of airfoil surface

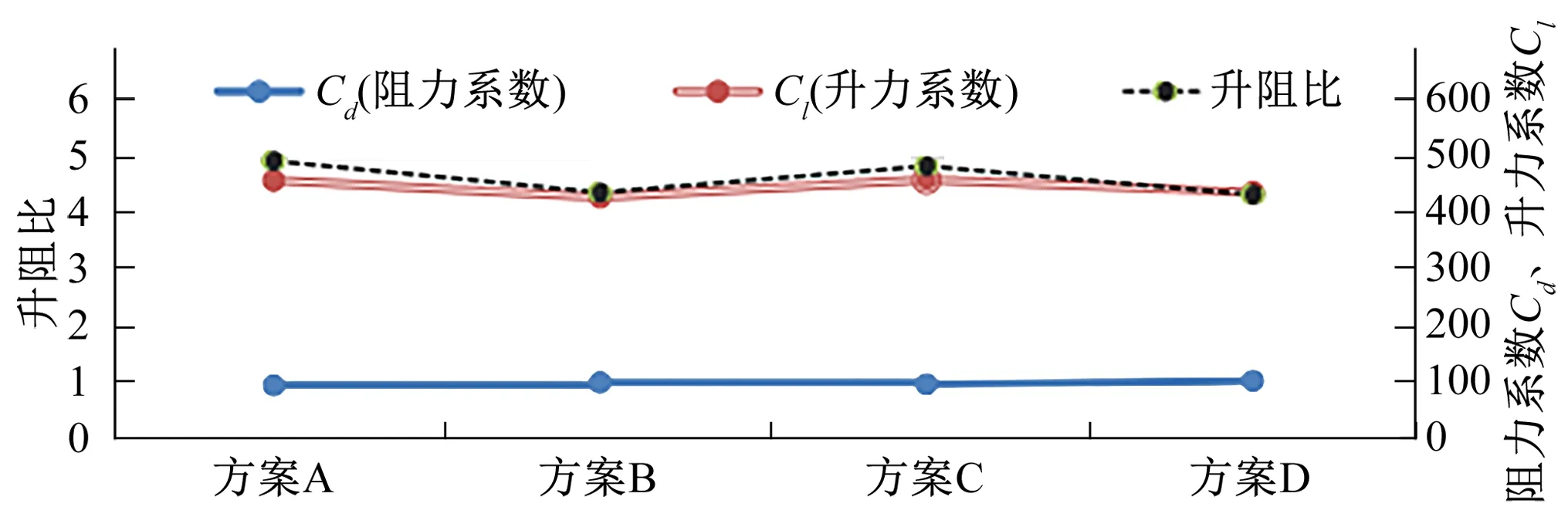
图13 4种方案对应的变化曲线Fig.13 Corresponding variation

4 结 论

根据以上的数值模拟及分析可以得出以下结论。

(1)本文对三维翼形进行了空化模拟，初步表明现在的多相流模型及空化模型能够较好地模拟出三维翼形空化的情况，而不仅仅局限于二维或者单相流的模拟。

(2)本文对增加翼形表面粗糙度及增加微孔对翼形空化的影响进行模拟，模拟结果表明2者均能在一定程度上改善翼形空化的性能，但是增加翼形表面粗糙度对翼形的水力特性有一定程度上的减弱影响。至于孔数的多少、位置及粗糙度的大小等因素对翼形空化的影响还有待进一步研究。

(3)将本文结果初步应用到流体机械上，可优先考虑给叶片空化区增加微孔，再考虑增加叶片空化区的粗糙程度，这样可以减少这些措施对叶片水动力性能的影响，但具体实施还需视具体情况而定。