微孔板图片微孔中心的精确定位方法

郭玉彬，曾晓银，吴少乾，李西明，王璇

（华南农业大学，广州 510642）

0 引言

微孔板是一种多用途的检测试验板，在临床实验、化学试验、兽医的试剂检测等方面均有广泛的应用。而随着人工智能的发展，临床实验的工作人员对智能化自动化的实验需求越来越高。实现微孔板智能化识别可以加快临床实验的人工智能化，大大解放实验工作人员的劳动力，推动社会的发展。进一步地，精确定位微孔板的孔圆心可以快速提取圆孔内的实验试剂，将实验数字化，便于机器的学习及机器的智能识别，使临床实验的智能化自动化成为可能。

对微孔板的微孔圆心的定位，实际上就是一种特殊的前景与背景的图像分割（前景是指圆孔，而背景是非圆孔）。在图像分割方面，国内外的研究大多数都是基于机器学习算法的图像分割，例如汪粼波、郭延文、夏天辰等人提出的样本驱动的半自动图像集前背景分割方法[6]，通过手动分割样本的前景和背景，利用SVM训练分类，从而实现半自动图像集的前背景分割；覃晓、梁伟、元昌安等人提出的基于遗传优化谱聚类的图形分割方法[7]，通过对谱聚类算法的优化，将遗传算法应用于谱聚类算法以提高谱聚类的图像分割质量；许雪梅、黄征宇、李丽娴等人提出的一种基于HSV颜色分割和模糊级联分类器的人脸检测技术[8]，通过对图像选择性光线补偿，并利用HSV进行肤色检测，在形态学处理及特征比例筛选后通过模糊级联分类器进行分割人脸与图像的背景，从而实现人脸检测。但是利用机器学习需要大量样本作为训练，而微孔板的使用是一次性，因此通过机器学习算法来定位圆孔中心不是很好的方法。另外，微孔板圆孔的背景包括实验台及微孔板，而微孔板本身的特征和圆孔的特征相似，这些方法都很难从相似的背景（微孔板）中分割出圆孔。为了解决这一难题，以及提高识别圆孔的精度，本文以一种全新的思路，充分利用已知的微孔板与圆孔之间的比例不变的关系，提出了一种自然拍照的微孔板图片中微孔中心的精确定位方法。

1 算法主流程

1.1 思路解析

如图1所示，由于圆孔在微孔中的位置都是固定的，因此，通过计算出圆孔半径与微孔板边长的比例，以及各个圆孔的圆心位置在整个微孔板中相对比例，则便可在一张标准的微孔板图片中标出各个圆孔的中心了。

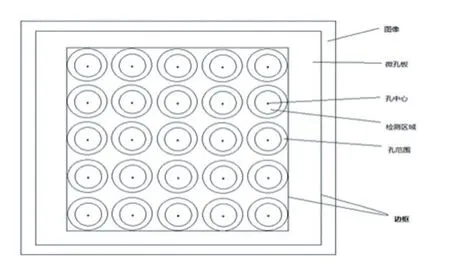
图1 模具示意图

本算法就是充分利用微孔板的圆孔与微孔板之间的比例不变关系，将要解决的问题即如何精确定位微孔板的各个孔中心转换为如何精确定位微孔板的矩形边界（这大大降低了问题的复杂度，使算法的效率大大提高）。如果矩形边界精确定位后，则可将矩形的图像，即整个微孔板通过标准透视变换提取出来，再根据微孔板的相应比例通过数学简单计算便可直接标出微孔板的孔中心，从而实现自然拍照的微孔板图片中微孔中心的精确定位。

在定位矩形边界这个问题上，可以根据前人的研究[1-5]，利用图像处理技术与直线拟合检测的方法进行矩形边界的定位，通过对图像进行预处理并除去相关噪点，再利用直线拟合找到微孔板矩形的边界，从而实现矩形的边界定位。

1.2 算法主要步骤

如图2所示，该算法主要由图像预处理、直线拟合检测矩形、计算并标出孔坐标这三大部分构成。最终，可通过该算法精准地获取矩形微孔板的边界线，并定位好微孔板中心区域各孔位置，继而提取出各个圆孔内的样品溶液图片。

2 算法实现

2.1 图像预处理

图像预处理主要是将图像简化并删除图像中的噪点，突出图像的特征信息。如图3所示，图像预处理包括读取图像、转换灰度图、二值化处理及除去噪点四步：

（1）读取图像：读取一幅图像。

（2）转换灰度图：将读取的图像转换为灰度图。

（3）二值化处理：先对灰度图进行高斯低通滤波处理，再使用Canny算子对边缘进行二值化处理。

（4）除去噪点：计算并对图像的连通区域进行面积大小排序，将80%～90%的小连通域毛刺删除掉，只保留主连通域。

图2 算法主流程图

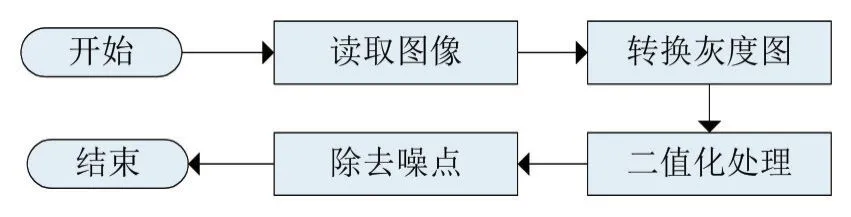
图3 图像预处理流程图

2.2 直线拟合检测矩形

计算直线求交点是孔定位当中至关重要的一步，如果边界线定位不精确，那么便会导致定位的微孔板圆心也会出现偏差。但上一阶段的图像预处理大大地删除了噪点，为这一步的直线拟合的准确性做了大大的保证。因此，通过简单的隔点拟合直线的方法便可精确地求出边界线了。如图4所示，隔点拟合直线主要分为以下四步：

（1）获取基准点：从上下左右四个方向分别做像素点检测，遇到像素为1的像素点则停止检测，并记录该位置，继续下一个像素点的获取，这样便可获得四组基准点。

（2）隔点连线：由于考虑到相邻两点所做的直线偏差过大，因此各组分别提取每相隔5个点的两点来拟合出多条直线，但各组只保留直线上点数最多的一条作为该组的边界线，从而得出矩形的四条边界线。

（3）求出矩形顶点：对这四条边界线进行相邻组合成方程组，求出这两条直线的交点，即顶点。

图4 直线拟合检测矩形流程图

2.3 计算孔坐标

基于上一阶段的矩形定位，可通过透视变换对矩形进行标准矫正，即可提取出标准微孔板图片。通过微孔板的标准比例即可计算出圆孔坐标。如图5所示，计算孔坐标可以分为以下3个步骤实现：

（1）透视变换：利用标准微孔板的长宽比例，将上一阶段识别的矩形图像透视变换成符合相应比例的微孔板图像。

（2）求出孔坐标：根据标准微孔板的比例关系，求出微孔板图像中各个圆孔的半径长度及中心坐标。

（3）霍夫检测：（此步骤可省略）此步骤是对矩形边界识别不准确的一种保障方法，霍夫检测可以降低由于矩形边界识别不准确导致计算的坐标误差，提高本算法的精确度及灵活性，减少对矩形边界的依赖性。

图5 计算孔坐标流程图

3 实验结果与分析

3.1 测试结果

（1）测试硬件环境：PC C4 1.7G，内存4G，机械硬盘500G

（2）测试软件环境：Windows7 系统，.NET Framework 3.5，MATLAB2017a，OpenCV3.20

（3）结果：为了验证本算法的正确性和高效性，自然拍摄兽医学院的120张实验微孔板图片作为样本测试，其中准确定位出微孔板矩形的有100张图片，准确定位出各个圆孔圆心的有117张，可见微孔板矩形的准确率为83%，圆孔圆心的准确率98%，在矩形偏差情况下成功通过霍夫变换纠正圆孔圆心的矫正率为85%，其中霍夫变换可以将圆心的准确率大约提高15%。另外，测试完120张图片一共花费了50秒，平均定位一张图片大概为416毫秒。

3.2 预处理结果与分析

如图6所示，它是预处理后的图像。从这张图中，可以发现预处理效果是非常好的，基本上把微孔板的边界的特征都完好保留下来。

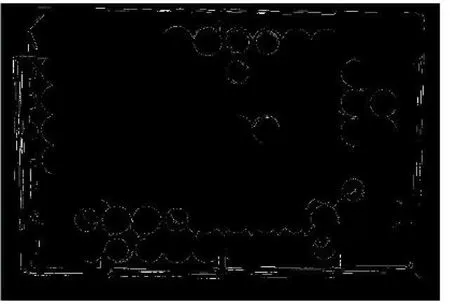
图6 预处理效果图

3.3 直线拟合检测矩形结果与分析

如图7所示，它是定位微孔板矩形边界的其中一张效果图（其中微孔板边界用白色虚线标注）。从这幅图中，可以发现微孔板矩形边界的定位是相当精准的，在测试的120张图片中，只有20张识别不准（大部分图片是由于微孔板过于偏斜导致，有两三张是由于拍摄的图片噪点过多，导致直线拟合失败），其他的都相当精准。

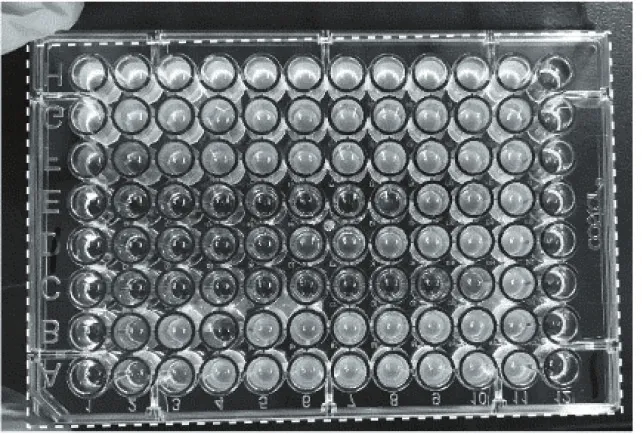
图7 识别矩形边界效果图

3.4 计算孔坐标结果与分析

如图 8（a）、8（b）所示，8（a）表示矫正后的标准微孔板图，8（b）表示在标准微孔板中所计算出的微孔中心坐标的效果图（图中白色的实线圆圈所示）。从图8（a）的结果展示，可以发现矫正后的矩形可以使微孔板的圆孔定位变得非常简单，另外从定位的效果图可以看出所定位出的半径及圆心是相当准确的。

4 结语

本算法利用微孔板的固定比例，将定位圆孔转换为定位微孔板的矩形边界，从而简化了问题，提高了圆孔与非圆孔图像分割的准确率，同时也为分割一个位置相对固定的子图像提供一种比例方法的提取思路。但从效果上看，本算法还存在一点毛刺，例如这种简单的矩形检测只能适用于这种背景简单的检测，对于复杂或图片质量很差的微孔板的边界检测效果就会变差了，虽然霍夫变换可以提高准确率，但那也是得在偏差很小的情况下才能矫正。因此，如果要保证圆心定位的准确率达到99%，甚至100%，那么就要保证微孔板矩形边界识别的准确率至少达到95%以上，这也是下一步要研究的方向，即如何精准识别微孔板的矩形边界。

图8