一价镧离子高n里德伯态*

2019-03-16李晓康贾凤东余方晨李明阳薛平许祥源钟志萍

物理学报 2019年4期

关键词：本征能级电离

李晓康贾凤东余方晨李明阳薛平许祥源钟志萍 4）‡

1）(中国科学院大学物理科学学院,北京 100049）

2）(清华大学物理系,低维量子物理国家重点实验室,量子物质科学协同创新中心,北京 100084）

3）(首都师范大学物理系,北京 100037）

4）(中国科学院大学,中国科学院拓扑量子计算卓越创新中心,北京 100190)

基于五步激光共振激发,经由中间态(Xe) 的一价镧离子光谱,分析了该实验谱,确定了一价镧离子一强一弱两个自电离里德伯系列.同时利用多通道量子亏损理论(MQDT)框架下的相对论多通道理论(RMCT)计算,标识了这两个自电离里德伯系列,强的自电离里德伯系列标识为.根据实验谱峰数据,发现有效量子数很高时,里德伯和自电离里德伯能级量子数亏损随激发能量不平滑变化,并分析了可能的原因.

1 引言

镧元素属于稀土元素,稀土元素最外层电子结构和碱土金属原子相似,但稀土金属原子的次外层并未被电子填满,因此稀土元素的原子及其离子的光谱复杂,具有一般元素没有的现象和特性.稀土元素的光谱数据在天体物理中有重要研究价值,镧及其化合物在材料科学、冶金、化工等领域有重要应用.Xie等[1]采用五步激光共振激发方式将镧原子从基态激发到一价镧离子第一电离阈值附近,有两种激发方案:一个是经过一价镧离子中间态(Xe)激发;另一方案是经过一价镧离子中间态(Xe)激发.文献[1]根据经过一价镧离子中间态(Xe)激发的光谱,拟合了89970—90080cm–1能区 15 个里德伯态的能级,得到一价镧离子第一电离阈值,该数值被美国国家标准与技术研究院推荐为一价镧离子第一电离阈值[2].在多通道量子亏损理论(MQDT)[3−9]框架下,利用相对论多通道理论 (RMCT)[10−16],文献 [17−20]计算了一价镧离子的束缚能级和自电离光谱,对两种方案的一价镧离子实验光谱做了标识.需要指出的是,以往关于一价镧离子谱数据研究主要是报道了谱峰位置及标识,本文研究一价镧离子的里德伯态和自电离里德伯态的量子数亏损随激发能量的变化趋势.众所周知,具有至少一个电子处于高激发态,即主量子数很高的里德伯态,是类氢体系,具有相似的特性.并且里德伯原子的偶极矩很大,对外场很敏感,因此广泛应用于精密测量,例如近年来利用里德伯原子测量微波电场[21,22].外场的存在在光谱中的显著体现是能级移动,破坏里德伯能级的规律性,这从里德伯系列的量子数亏损光滑性的破坏上可以看出.事实上,本文发现有效量子数很高时,一价镧离子里德伯和自电离里德伯能级的量子数亏损随着激发能量不是平滑变化的,并初步探讨了可能的原因.

2 实验方法和理论方法

2.1 实验方法

采用电热原子化获得镧蒸气[1]:镧原子的熔点只有 918℃,沸点却高达 3464℃.由于熔点和沸点的温差很大,只需将加热温度控制在熔点以上,就可获得非常稳定的原子束.在实验中用120A的交流电加热,使坩埚温度控制在约 1200℃.加热后产生的镧原子经过准直孔后形成准直的原子束进入共振激发区域.在这个区域中,原子束与激光垂直相交以避免多普勒效应的影响.采用五步激光共振激发方式将镧原子从基态激发到一价镧离子第一电离阈值附近[1],有两种激发方案,一个是经过一价镧离子中间态(Xe)激发到一价镧离子第一电离阈值附近;另一方案是经过一价镧离子中间态(Xe)激发到一价镧离子第一电离阈值附近[1].具体激发方案是:

当激光激发完成后,一个弱脉冲场将所有离子引导到一个很强的直流场(50kV/cm),弱的脉冲电场不足以将里德伯离子电离,而强的直流场可以将有效量子数的离子里德伯态电离成二价离子,所有离子经过飞行时间质谱仪后由微通道板 (microchannel plate,MCP)收集,离子信号由于MCP的倍增效应被放大,MCP具有很高的时间分辨率(<100ps),单片MCP的倍增系数可达约104,由此区分镧原子电离产生的La+和由一价镧离子激发到高激发态电离产生的La2+信号,得到几乎纯净的一价镧离子激发光谱[24].对于不同能区激发谱,施加的场电离条件有所不同,因此得到的MCP信号有差异,这就是测量的两段有重叠能区的光谱信号强度有差异的原因,如图1所示.为了对实验中扫描的激光波长进行定标,引出少量光利用 F-P标准具(自由光谱程约0.64cm–1)作相对定标,并利用空心阴极灯的光谱线进行绝对定标.实验时整个装置保持在真空度优于 6.7×10–4Pa的真空中,杂散电场小于 0.1V/cm[25],实验使用的染料激光器的线宽为0.5cm–1.

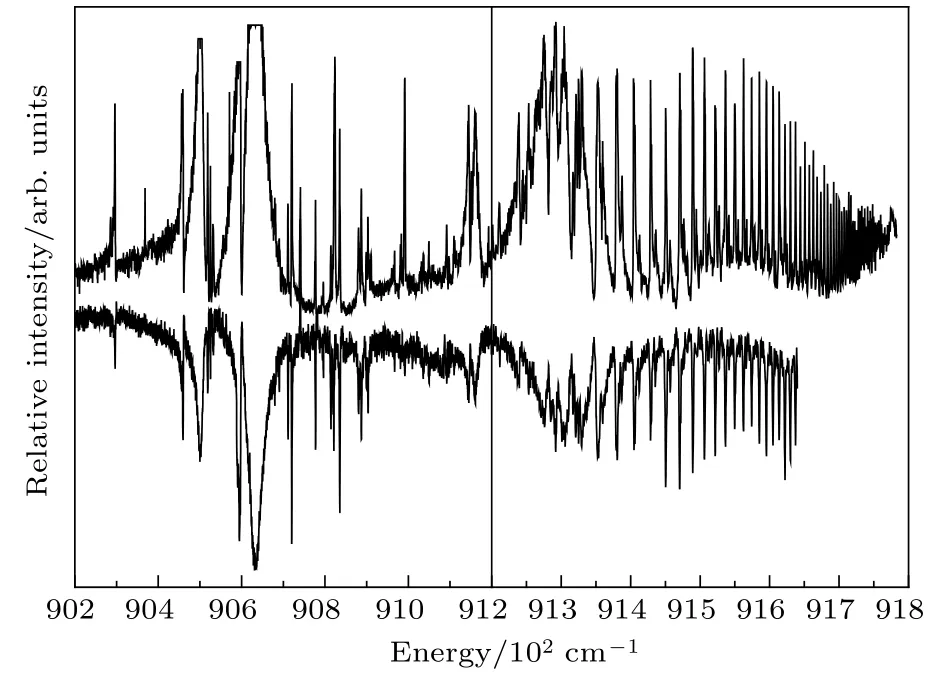
图1 由中间态 (Xe) 激发的一价镧离子光谱的能量标定:以文献 [1]的 89690.4—91639.8cm–1光谱 (下图 )为基准 ,对 89872.8—91783.2cm–1能区光谱 (上图)[19]重新标定,平移了–10.3cm–1.横轴能量以一价镧离子基态能量为零点Fig.1.The energy calibration of the excited La+spectrum via intermediate state (Xe) .We recalibrate the spectrum[19]in the energy region 89872.8 —91783.2 cm–1(upper figure) according to the spectrum[1]in the energy region89690.4—91639.8cm–1(lower figure),and the offset of the recalibration is–10.3cm–1.The zero point of energy is taken the energy of the ground state of La+.

2.2 理论方法

研究电子-电子关联作用是原子分子物理长期以来基本的研究课题之一.组态相互作用计算是公认的研究电子间关联效应的重要方法,在多通道量子亏损理论(MQDT)[3−9]框架下的相对论多通道理论(RMCT)[10−16],是把组态相互作用转化为通道间的相互作用.通道由一系列里德伯态及相应的连续态构成:原子实处于特定状态,激发电子角动量以及它与原子实角动量的耦合方式一定,而激发电子轨道能量不同.也就是说,某一通道中的一系列态,其原子实处于特定状态,激发电子角动量以及它与原子实角动量的耦合方式一定,而激发电子的轨道能量不同.

在多通道量子亏损理论(MQDT)[3−9]框架下,引入本征通道这个概念.本征通道的物理图像可以理解为:在第个本征通道中,作用域内较强的相互作用,使得在作用域外所有分解通道的电子径向波函数成为具有共同相移的库仑驻波,在各个分解通道中的库仑驻波则以特定的权重线性叠加在一起(下角标 i 表示各分解通道).因此所有的本征通道能够有效地描述在作用域内复合体的动力学特性,一个特定的本征通道可用一组紧致的物理参数,即MQDT参数定量地描述:短程散射矩阵的本征值(即本征量子数亏损)和其本征矢量(所有本征矢量组成正交的转换矩阵)以及偶极跃迁矩阵元.在阈值附近这些参数随能量是光滑变化的.相对论多通道理论(RMCT)[10−16]不仅考虑了有限束缚类组态的相互作用,而且考虑了无限多的里德伯态和相应的连续态的相互作用,由此可以计算有限能量点的MQDT参数,从而在MQDT框架下得到某一通道的无限多个里德伯态的能级.通道原则上是无限多的,但实际计算中只能考虑有限个通道.首先要考虑价电子和满壳层原子实各个电子的相互作用,而不考虑原子实内各电子的相互作用,这就是冻结实近似.但仅考虑冻结实近似是不够的,事实上原子实和激发电子之间的相互作用会造成原子实的改变,这其中比较重要的有动态极化效应[13]和伸缩模效应[26],分别由激发电子对原子实的极化和贯穿作用引起.具体地,动态极化效应是指激发电子围绕原子实运动产生的电场使得原子实的角动量变化,同时为保持原子总角动量和总宇称的守恒,激发电子的状态也发生相应的变化.其中( l 是原子实的角动量),称为偶极极化效应,称为四极极化效应等等[13−27].伸缩模效应是指激发电子贯穿到原子实内部,由于激发电子的屏蔽作用,原子实中的电子激发到更高能级的轨道,同时原子实的角动量和宇称保持不变,即主量子数改变,而原子实和激发电子角动量以及耦合方式不变[26,27].

我们已经在多通道量子亏损理论(MQDT)[3−9]框架下,利用相对论多通道理论 (RMCT)[10−16]计算了一价镧离子的里德伯能级和自电离光谱[17−20].其中文献[17]只考虑了收敛于一价镧离子的最低两个电离阈值的相关通道,即仅考虑了冻结实近似.而文献[18]考虑了冻结实近似、偶极极化效应和四极极化效应,包括了收敛于一价镧离子最低七个电离阈的所有可能通道,[19,20]以文献[18]考虑的通道计算为基础,计算了一价镧离子的光谱(代表电子总角动量,表示宇称,分别表示偶宇称和奇宇称),由此标识了两个激发方案得到的实验光谱.本文采用文献[19]的计算结果,分析和标识能量重新标定的经由中间态(Xe)激发的 89872.8—91783.2cm–1实验光谱.对于自电离谱峰的标识,以起主要作用的本征通道谱来标识,这在组态相互作用不是很强时可以满足标识自电离谱峰的要求.用此方法,我们标识了复杂原子钪原子[28]、锑原子[29]和镥原子[30]的自电离里德伯能级.考虑本征通道谱之间的相互作用,当激发能区远离原子实激发,散射截面是[4,6,8,9]

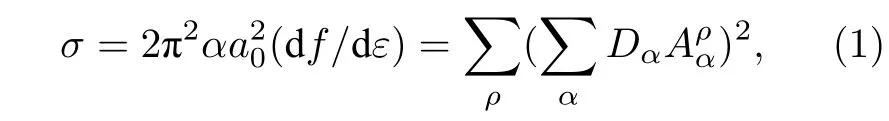
3 结果与讨论

根据能量重新标定的89872.8—91783.2cm–1实验光谱,我们重新确定了一强一弱两个自电离里德伯系列的谱峰位置,如表1和表2所列.通过比较实验谱和RMCT计算得到的本征通道谱,标识这两个自电离里德伯系列,其中强的自电离里德伯图2给出了与强自电离里德伯系列对应的本征通,可以看出理论和实验的谱峰位置大致对应,但强度和谱峰形状有较大差异.进一步定量比较量子数亏损的差异,采用一价镧离子的第二电离阈值 91816.03cm–1,这是基于美国国家标准与技术研究院[2]给出的二价镧离子能级和一价镧离子第一电离阈值推算得到的.从图 3 可以看出,当有效量子数时,实验能级得到的量子数亏损与理论计算的量子数亏损之差普遍小于 0.1.当时,随着激发能量增加而急剧增加,原因见后面分析.图1显示的实验光谱,有明显的干扰态存在.文献[19]识别了三个干扰态,对应实验谱的三个宽峰A,B 和 C,分别位于 90600,91300和 91600cm–1,文献[19]基于RMCT计算,给出了这三个干扰态的标识:峰 A 标识为,峰 B 标识为和 /或,峰C标识为.这样可以确定对实验谱有主要贡献的本征通道,考虑这些本征通道谱相互作用.具体地,根据 (1）式,在感兴趣能区取为常数,通过调整值,可以得到谱峰位置、谱峰强度和谱峰形状均接近实验谱的理论谱,如图2所示.这个理论谱考虑了的这些本征,相应的偶极跃迁矩阵元分别为0.5,0.01,10,0.1,0.1,10,–3,2 和–10.注意理论光谱卷积了仪器函数,该函数为高斯线形,半高全宽为实验使用的激光线宽0.5cm–1.从图2可以看出,考虑了干扰态影响的理论光谱,强自电离里德伯系列能级对应的谱峰位置与相应本征通道谱的谱峰位置在谱峰宽度内一致.因此不再列出考虑了干扰态影响的理论光谱对应的谱峰位置.

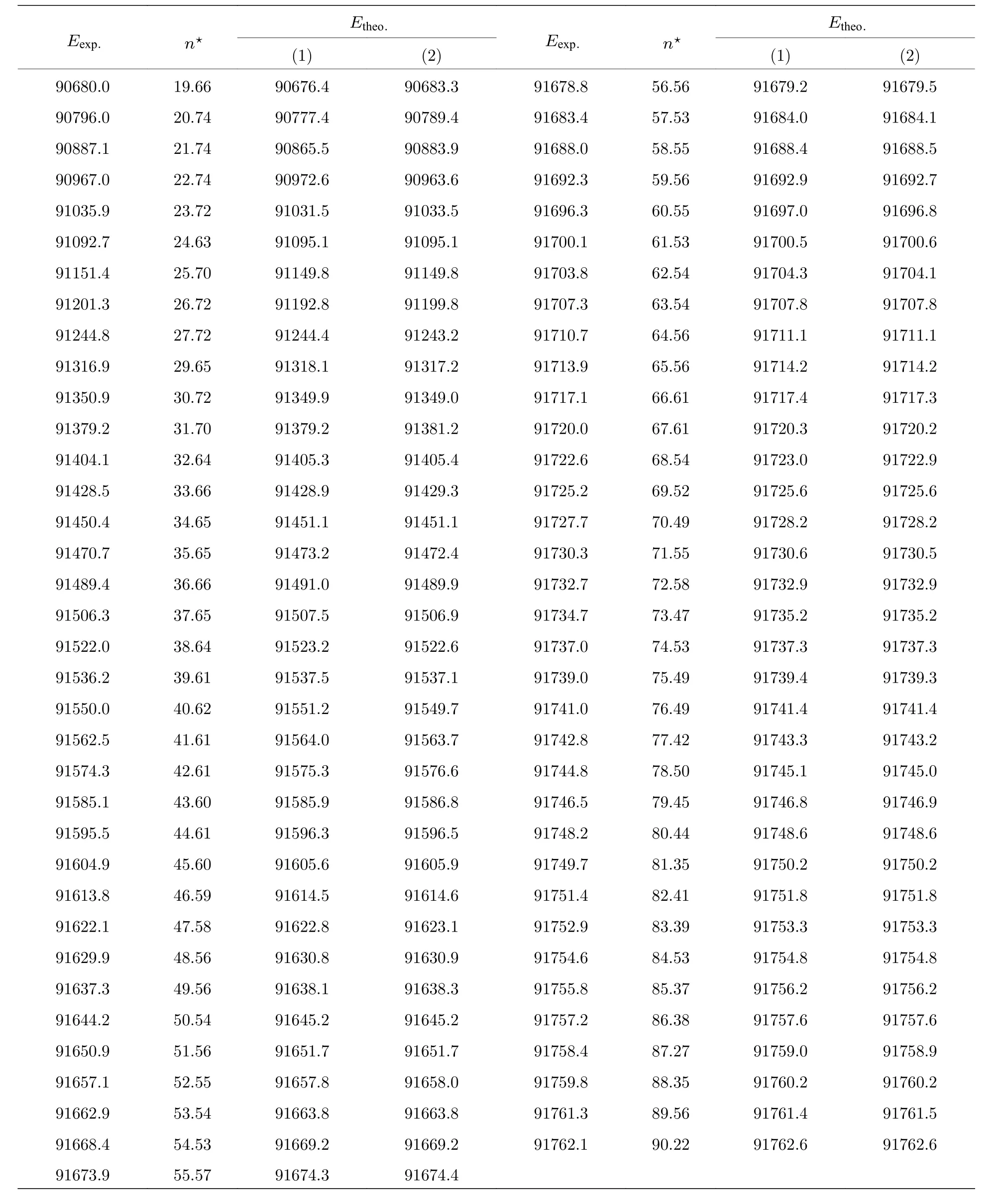
表1一价镧离子强自电离里德伯系列能级位置实验和理论比较.理论标识分为两列:(1）本征通道实验能级由中间态(Xe) 激发的光谱得到.实验误差为0.5cm–1Table1. Comparison of energy positions(cm–1)between the experimental and the theoretical strong autoioniz(ation Rydberg series of La+.Theoretical assignments are divided into two columns with the labels:(1）eigenchannel ,(2）eigenchannel .The experimental energy levels are obtained via the intermediate state(Xe) .The experimental error is0.5cm–1.

90680.0 19.66 90676.4 90683.3 91678.8 56.56 91679.2 91679.5 90796.0 20.74 90777.4 90789.4 91683.4 57.53 91684.0 91684.1 90887.1 21.74 90865.5 90883.9 91688.0 58.55 91688.4 91688.5 90967.0 22.74 90972.6 90963.6 91692.3 59.56 91692.9 91692.7 91035.9 23.72 91031.5 91033.5 91696.3 60.55 91697.0 91696.8 91092.7 24.63 91095.1 91095.1 91700.1 61.53 91700.5 91700.6 91151.4 25.70 91149.8 91149.8 91703.8 62.54 91704.3 91704.1 91201.3 26.72 91192.8 91199.8 91707.3 63.54 91707.8 91707.8 91244.8 27.72 91244.4 91243.2 91710.7 64.56 91711.1 91711.1 91316.9 29.65 91318.1 91317.2 91713.9 65.56 91714.2 91714.2 91350.9 30.72 91349.9 91349.0 91717.1 66.61 91717.4 91717.3 91379.2 31.70 91379.2 91381.2 91720.0 67.61 91720.3 91720.2 91404.1 32.64 91405.3 91405.4 91722.6 68.54 91723.0 91722.9 91428.5 33.66 91428.9 91429.3 91725.2 69.52 91725.6 91725.6 91450.4 34.65 91451.1 91451.1 91727.7 70.49 91728.2 91728.2 91470.7 35.65 91473.2 91472.4 91730.3 71.55 91730.6 91730.5 91489.4 36.66 91491.0 91489.9 91732.7 72.58 91732.9 91732.9 91506.3 37.65 91507.5 91506.9 91734.7 73.47 91735.2 91735.2 91522.0 38.64 91523.2 91522.6 91737.0 74.53 91737.3 91737.3 91536.2 39.61 91537.5 91537.1 91739.0 75.49 91739.4 91739.3 91550.0 40.62 91551.2 91549.7 91741.0 76.49 91741.4 91741.4 91562.5 41.61 91564.0 91563.7 91742.8 77.42 91743.3 91743.2 91574.3 42.61 91575.3 91576.6 91744.8 78.50 91745.1 91745.0 91585.1 43.60 91585.9 91586.8 91746.5 79.45 91746.8 91746.9 91595.5 44.61 91596.3 91596.5 91748.2 80.44 91748.6 91748.6 91604.9 45.60 91605.6 91605.9 91749.7 81.35 91750.2 91750.2 91613.8 46.59 91614.5 91614.6 91751.4 82.41 91751.8 91751.8 91622.1 47.58 91622.8 91623.1 91752.9 83.39 91753.3 91753.3 91629.9 48.56 91630.8 91630.9 91754.6 84.53 91754.8 91754.8 91637.3 49.56 91638.1 91638.3 91755.8 85.37 91756.2 91756.2 91644.2 50.54 91645.2 91645.2 91757.2 86.38 91757.6 91757.6 91650.9 51.56 91651.7 91651.7 91758.4 87.27 91759.0 91758.9 91657.1 52.55 91657.8 91658.0 91759.8 88.35 91760.2 91760.2 91662.9 53.54 91663.8 91663.8 91761.3 89.56 91761.4 91761.5 91668.4 54.53 91669.2 91669.2 91762.1 90.22 91762.6 91762.6 91673.9 55.57 91674.3 91674.4

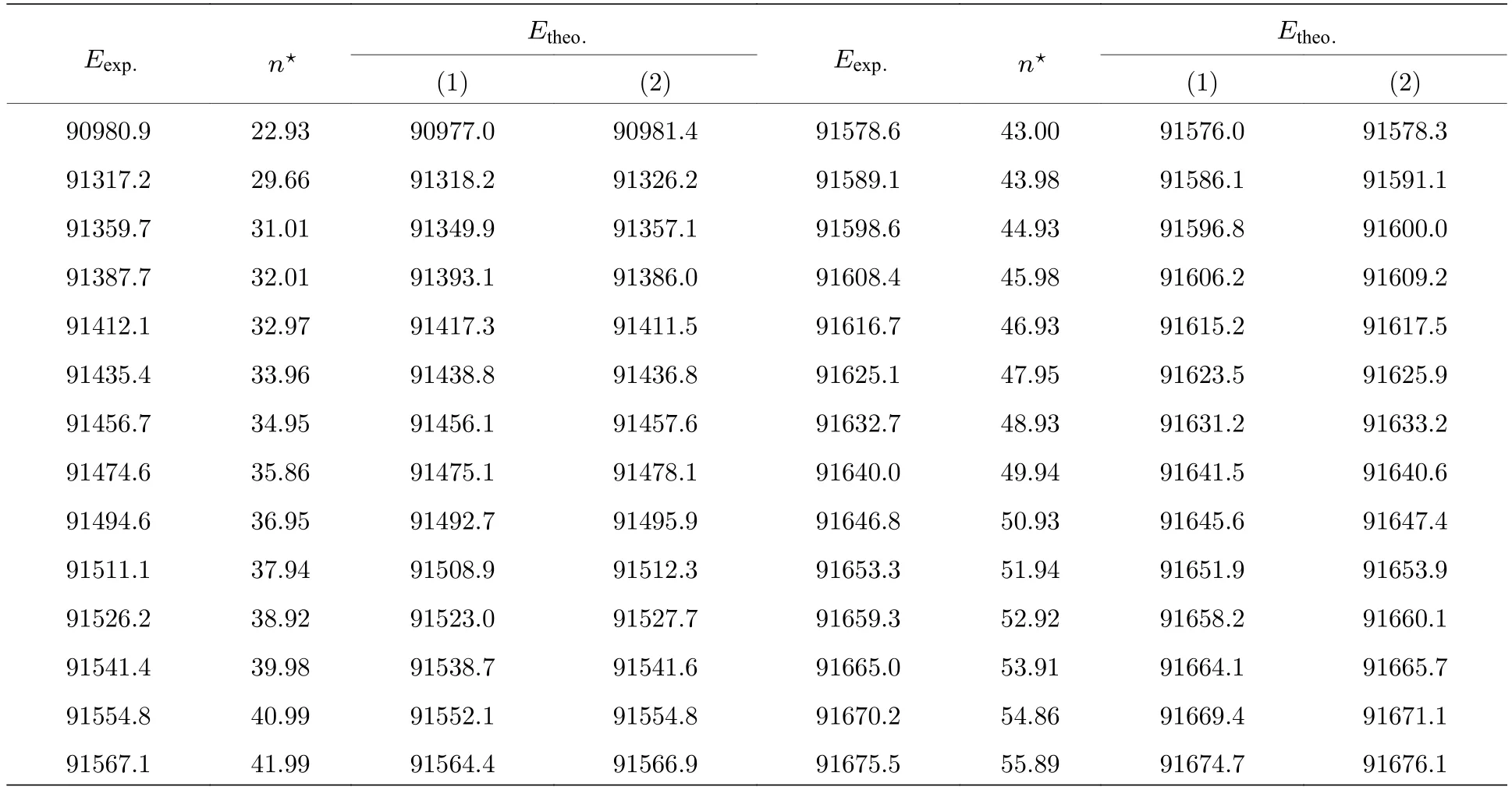
表2 一价镧离子弱自电离里德伯系列能级位置实验和理论比较.理论标识分为两列:(1）本征通道 ,(2）本征通道 .实验能级由中间态(Xe) 激发的光谱得到.实验误差为0.5cm–1Table2. Comparison of energy positions(cm–1)between the experimental and the theoretical weak autoioniz(ation Rydberg series of La+.Theoretical assignments are divided into two columns with the labels:(1）eigenchannel ,(2）eigenchannel .The experimental energy levels are obtained via the intermediate state(Xe) .The experimental error is0.5cm–1.

(1） (2）90980.9 22.93 90977.0 90981.4 91578.6 43.00 91576.0 91578.3 91317.2 29.66 91318.2 91326.2 91589.1 43.98 91586.1 91591.1 91359.7 31.01 91349.9 91357.1 91598.6 44.93 91596.8 91600.0 91387.7 32.01 91393.1 91386.0 91608.4 45.98 91606.2 91609.2 91412.1 32.97 91417.3 91411.5 91616.7 46.93 91615.2 91617.5 91435.4 33.96 91438.8 91436.8 91625.1 47.95 91623.5 91625.9 91456.7 34.95 91456.1 91457.6 91632.7 48.93 91631.2 91633.2 91474.6 35.86 91475.1 91478.1 91640.0 49.94 91641.5 91640.6 91494.6 36.95 91492.7 91495.9 91646.8 50.93 91645.6 91647.4 91511.1 37.94 91508.9 91512.3 91653.3 51.94 91651.9 91653.9 91526.2 38.92 91523.0 91527.7 91659.3 52.92 91658.2 91660.1 91541.4 39.98 91538.7 91541.6 91665.0 53.91 91664.1 91665.7 91554.8 40.99 91552.1 91554.8 91670.2 54.86 91669.4 91671.1 91567.1 41.99 91564.4 91566.9 91675.5 55.89 91674.7 91676.1(1） (2）

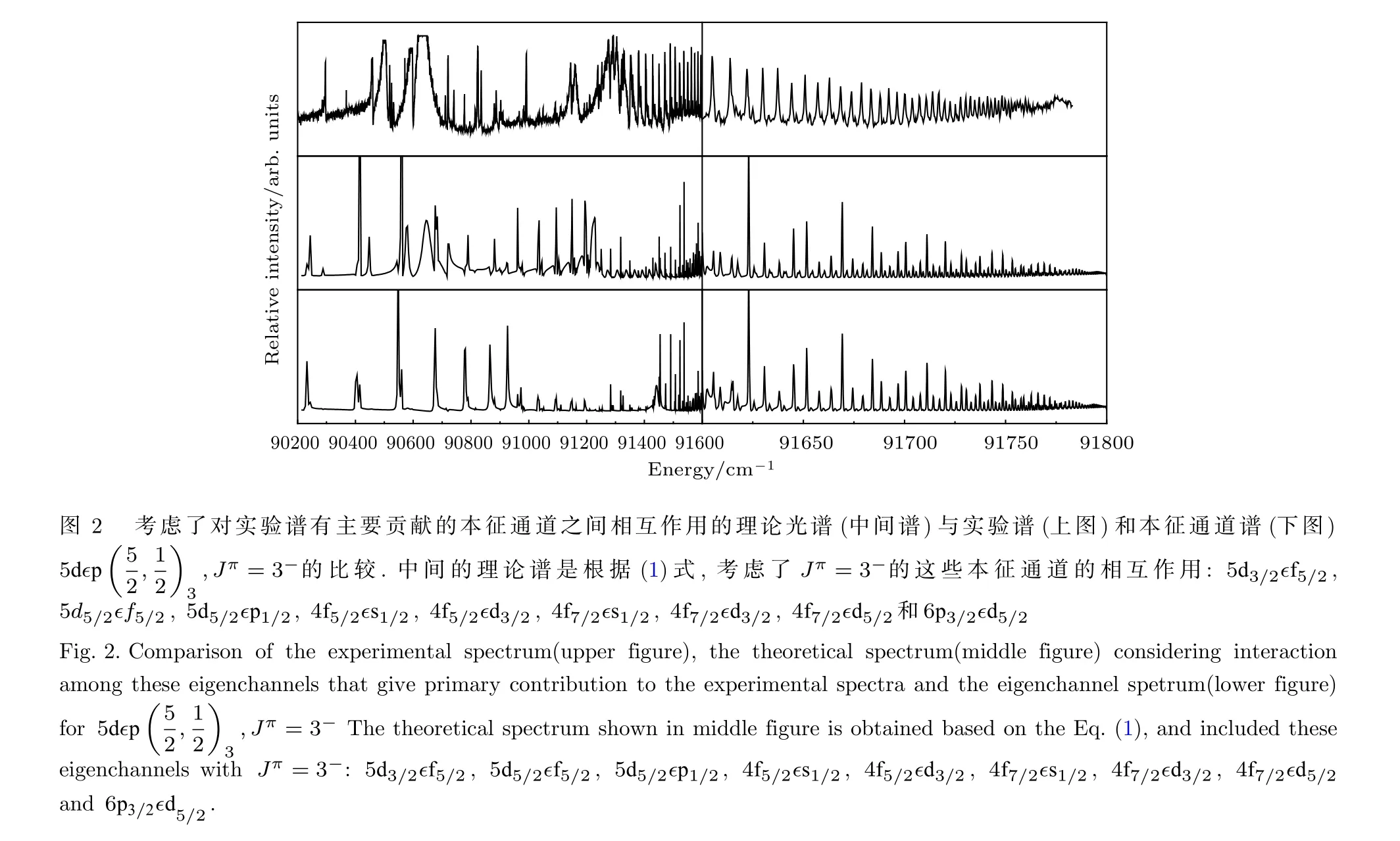
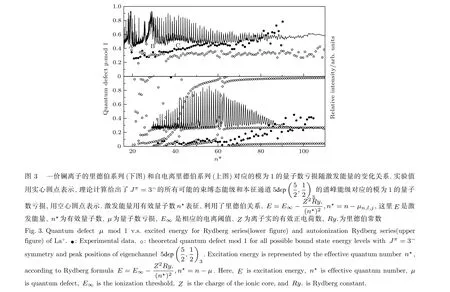
图3给出了一价镧离子的里德伯态和强自电离里德伯态的量子数亏损随激发能量()的变化规律.很明显,实验数据显示这两个里德伯系列在有效量子数很高()时,量子数亏损光滑性被破坏.具体来说,无论是一价镧离子的里德伯系列还是强自电离里德伯系列,有效量子数在67—90这段范围,量子数亏损变化了约0.4.实验光谱在有效量子数很高()时的异常还体现在:离子里德伯态在有效量子数时,自电离里德伯态在时,谱线明显展宽,相邻谱峰重叠明显.这一现象并不是激光线宽造成的,因为只有在,里德伯能级间隔才小于激光线宽(0.5cm–1).

首先排除组态相互作用对里德伯能级规则性破坏的贡献.考虑组态相互作用的RMCT计算显示:对离子里德伯系列,时,实验能级得到的量子数亏损与理论计算的量子数亏损之差普遍好于0.02,理论与实验符合非常好;如图3所示,在高的有效量子数()时,无论离子里德伯系列还是自电离里德伯系列,理论计算的量子数亏损均是平滑变化,但是实验能级得到的量子数亏损并不是平滑变化,因此量子数亏损光滑性被破坏并不是组态相互作用造成的.

上述证据强烈暗示外场的存在,这个外场不可能是杂散电场,因为它的强度很弱不足以解释实验现象(可根据文献[31]估计能级的斯塔克展宽).这个外场可能源于第二步激发过程中镧原子光电离产生的等离子体,是等离子体效应对里德伯能级影响的体现.处于等离子体环境中离子的能级结构以及动力学性质会受到周围等离子体环境的影响,其中一个基本现象是电离势降低(ionization potential depression,IPD).IPD 实验是等离子体物理学中一个长期存在的问题,而对IPD广泛采用的理论解释主要有两种半经典模型,分别是Ecker-Kröll(EK)模型[32]和 Stewart-Pyatt(SP)模型[33].近些年也有很多理论工作细致研究了等离子体环境对其中离子的能级结构以及动力学性质的影响,例如文献[34]通过理论计算研究了德拜等离子体环境中类氢离子束缚-束缚跃迁的性质,计算结果表明跃迁对应的谱线会发生红移.而一价镧离子里德伯态量子数亏损光滑性的破坏可能来源于等离子体环境造成的这类影响.激发能量与量子数亏损的关系由下面的里德伯公式给出：

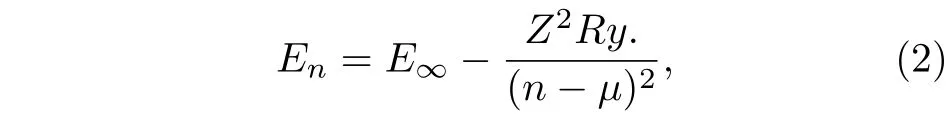
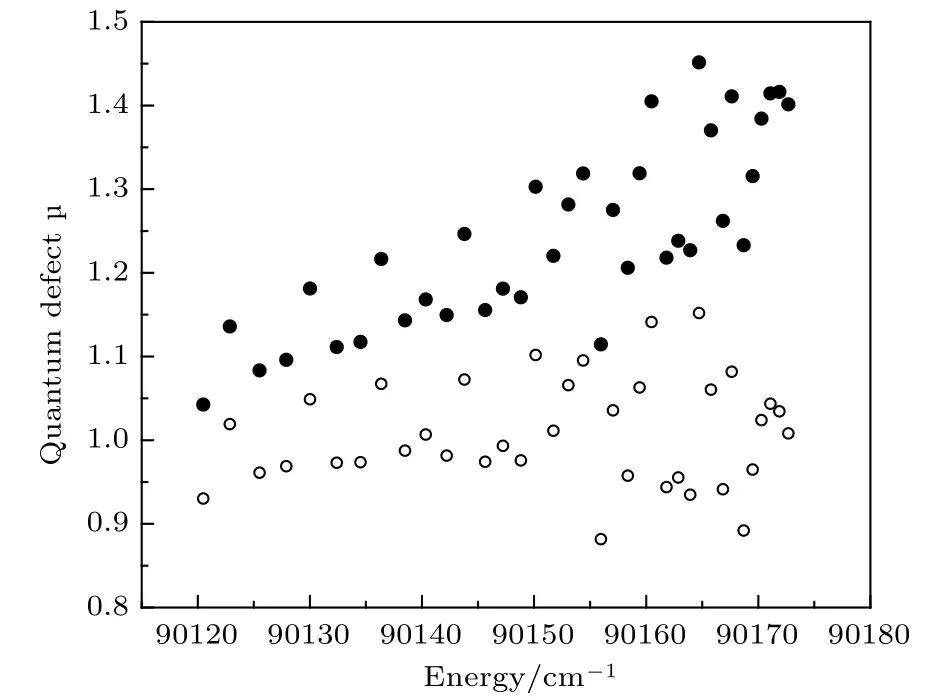
图4 不同电离阈值得到的一价镧离子里德伯系列(有效量子数时 ,对应激发能量范围为 90120cm–1—90175cm–1)量子数亏损随激发能量的变化关系.采用文献[1]给出的一价镧离子第一电离阈值90212.8cm–1,得出的量子数亏损用实心圆点表示;采用根据里德伯系列量子数亏损变化光滑性拟合的电离阈值90212.5cm–1,得出的量子数亏损用空心圆点表示Fig.4.Quantum defect v.s. excited energy for the Rydberg series( ,in the energy region90120cm–1—90175 cm–1) converging to the different ionization thresholds. :quantum defects obtained by the ionization threshold 90212.8 cm–1from Ref.[1]. :quantum defects obtained by the ionization threshold90212.5cm–1,which is fitted based on the quantum defect regular behavior for a Rydberg series.

事实上,当电离光能量在电离阈值附近时,光电离磁光阱的冷原子可以产生强耦合等离子体,这方面的实验研究已开展了近二十年,具体参见综述文章[35].文献[36]利用里德伯能级微波跃迁,测量了冷原子光电离产生的等离子体对里德伯能级的移动效应.进一步工作还在开展中.