高分五号卫星多角度偏振相机最优化估计反演:角度依赖与后验误差分析*

郑逢勋 侯伟真 李正强†

1）(中国科学院遥感与数字地球研究所,国家环境保护卫星遥感重点实验室,北京 100101）

2）(中国科学院大学,北京 100049）

3）(中国科学院遥感与数字地球研究所,遥感科学国家重点实验室,北京 100101）

多角度偏振相机(directional polarimetric camera,DPC)随高分五号卫星已经成功发射并持续获取全球观测数据.针对DPC在陆地气溶胶反演领域的应用需求,本研究基于多参数最优化估计反演框架,引入信息量和后验误差分析工具,讨论了DPC观测信息量对角度的依赖,给出了地表和气溶胶参数的后验误差,并分析了后验误差的影响因素.研究表明:1）卫星观测信息量随观测角度个数的增加显著提升,DPC多角度观测比单角度观测的总 DFS(degree of freedom for signal)平均提高了 5.45;2）气溶胶反演比地表更依赖于卫星观测几何,散射角覆盖范围越大,观测包含的气溶胶信息量越多;3）反演参数的后验误差随观测角度个数的增加显著降低,而气溶胶模型误差对后验误差的影响并不显著.总体来说,观测误差是影响反演结果不确定性的主要因素.本研究对DPC多角度偏振观测的反演能力以及反演不确定性进行了系统的定量评估,为DPC在轨测试及反演算法开发提供参考.

1 引 言

气溶胶是影响整个地球系统辐射平衡中最不确定的因素之一[1].获取满足全球或区域气候系统模型精度需求的气溶胶物理、光学特性需要更为全面的气溶胶观测数据,例如多角度偏振卫星观测[2−4].POLDER(polarization and directionality of the earth's reflectances)是国际上具备在轨多角度偏振测量能力的传感器[5−8],该卫星在2004—2013年间提供了大量全球范围的观测数据.与POLDER相比,我国高分5号卫星平台搭载的多角度偏振相机 (directional polarimetric camera,DPC)在多项指标上有所突破[9,10].高分5号卫星已经于2018年5月成功发射,在接下来的若干年中,DPC将为全球气候变化、污染传输和气溶胶特性研究等领域提供重要数据,是继POLDER之后全球多角度偏振观测数据的重要来源.顾行发等[11]针对DPC在轨定标方法开展了相关研究,文献[12−14]针对DPC航空观测数据开展了地表反射率模型的相关研究,Cheng等[15]开展了DPC航空数据的气溶胶反演研究.在DPC卫星发射后,迫切需要对多角度偏振观测系统的气溶胶反演能力开展定量化的评估.

研究表明,对于采用多角度观测模式的卫星传感器,有效观测角度个数及对应的观测几何会引起观测信息量的较大变化[16−19],另外,卫星反演依赖于一定的先验知识,而先验误差会进一步影响反演的不确定性[20].Li等[10]针对DPC传感器提出了多参数最优化估计反演框架,该框架基于最优估计理论[21],采用改进的地表反射率模型,联合多角度的辐射强度和偏振观测进行光谱气溶胶光学厚度(aerosol optical depth,AOD)等参数的反演.在此基础上,为了系统地理解DPC的气溶胶反演能力,需要考虑以下几个方面的问题:1）观测角度个数和观测几何对气溶胶反演的影响;2）测量误差对反演的影响;3）气溶胶和地表模型的先验估计误差对反演的影响.

针对上述问题,本研究基于最优化估计反演理论框架,引入信息量分析工具,从仿真和误差的角度系统分析了DPC观测信息量对观测角度个数的依赖,多角度观测地表和气溶胶参数的理论反演误差,以及观测角度个数、观测误差和气溶胶模型误差对反演误差的影响.通过联合多角度强度和偏振观测数据,对DPC的气溶胶和地表参数反演能力以及反演不确定性进行定量评估,为DPC反演算法的发展提供参考.

2 多角度偏振卫星观测及矢量辐射传输模型

DPC 采用 512×512 有效像元的探测器,地面幅宽达到 1850km.通过沿轨多次成像,DPC 实现对同一目标多达 12个角度的观测.同时,DPC采用滤光片–偏振片组合的方式,提供5个波段的强度观测以及3个波段的偏振测量.DPC基本观测参数如表1所列(P表示偏振测量通道).

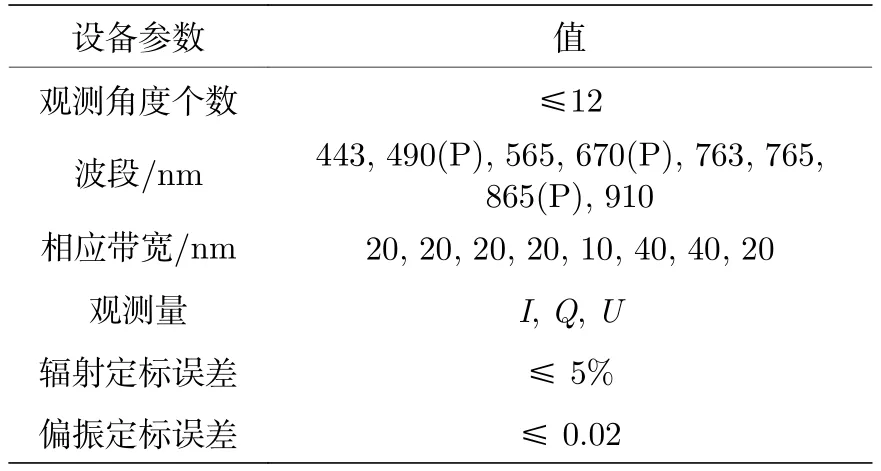
表1DPC 传感器的基本参数Table1. Basic characteristics of DPC sensor.

经过严格的几何校正和配准,DPC提供的L1级产品包含归一化Stokes矢量[22]的前三个分量I,Q和 U.I为总的辐射强度,Q和 U描述了光相对于主平面(由观测方向和太阳位置构成的平面)的偏振状态.由于Q和U与参考平面有关,对测量定标的精度要求较高,因此在实际反演中,通常采用不含偏振方向信息的偏振辐亮度Lp进行反演[23−26],其定义为:

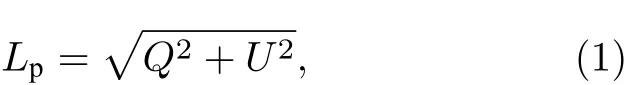
相应地,卫星观测的表观反射率和表观偏振反射率可以由下式计算得到:

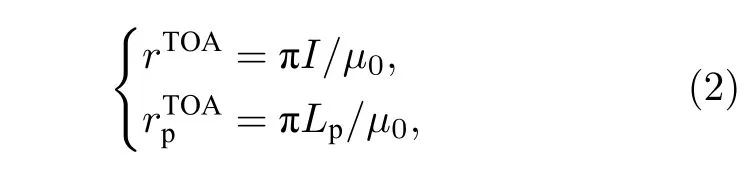
采用线性化的矢量辐射传输模型UNLVRTM(unified linearized vector radiative transfer model)[27]对 DPC 多角度偏振观测进行模拟.UNLVRTM在 VLIDORT(vector linearized discrete ordinate radiative transfer model)[28]的基础上进行开发,增加了 linearized Mie,linearized T-matrix,Rayleigh散射以及基于HITRAN(high-resolution transmission molecular absorption database)数据库的 line-by-line(LBL)气体吸收计算模块,形成了开源且易用的辐射传输模型.UNL-VRTM能够仿真 TOA(top of atmosphere)归一化的 Stokes矢量,同时计算出I,Q和U对模型参数的雅可比矩阵(Jacobian matrix),该模型已经在许多研究中得到应用和验证[29−33].

3 研究方法

3.1 地表模型

对于卫星偏振观测,本研究所采用的地表模型由强度和偏振两部分的贡献构成[16]:

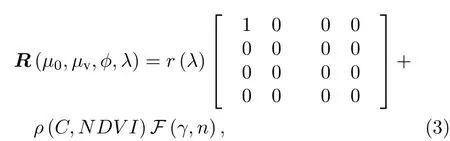
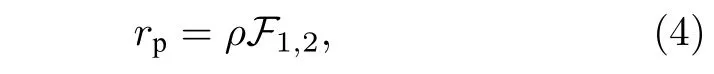
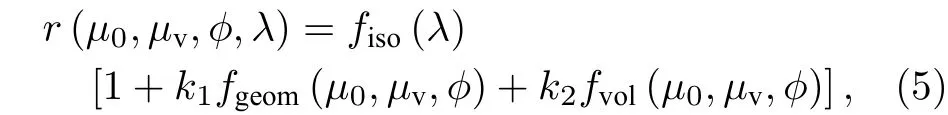
其中三个核函数fiso,fgeom和fvol分别代表各向同性散射、几何光学散射和体散射,k1和k2是两个与波长无关的系数,描述了地表反射率的各向异性.

3.2 气溶胶模型

采用球形粒子假设的双峰对数正态分布函数来描述气溶胶粒子谱:

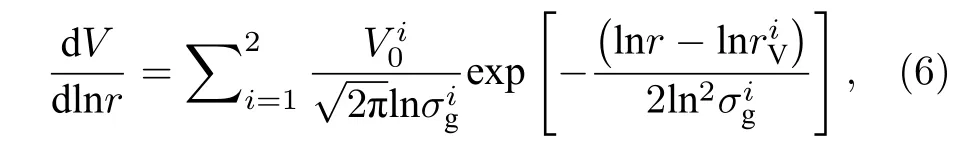
其中 i表示气溶胶模态,i=1 和 i=2 分别为细模态和粗模态;rV和分别为体积谱几何中值半径(单位为μm)和标准差.为了和前向模型采用的参数一致,采用有效半径reff和有效方差veff来代替(6）式中的rV和作为输入.二者的转换关系为:

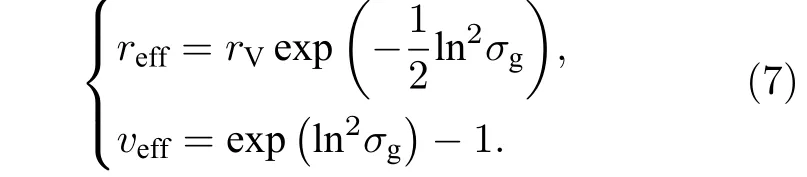
为方便描述,下文中以上角标f和c区分气溶胶细模态和粗模态,相应地,气溶胶总体积柱浓度为,细模态柱体积比气溶胶体积柱浓度是与波长无关的物理量,可以通过MIE散射计算得到气溶胶光谱AOD参数.复折射指数是影响气溶胶散射和吸收特性的重要参数,假设气溶胶复折射指数与波长无关,分别用表示细、粗模态气溶胶复折射指数的实部和虚部.

3.3 最优化估计模型

为了对DPC反演能力进行系统性的定量评估,引入最优化估计理论中的两个评价指标:自由度 (degree of freedom for signal,DFS)和后验误差 (posteriori error).其中,DFS 是对测量中包含的目标信息的定量描述,DFS越高,观测包含的目标信息越充分,通常,当某个参数的DFS大于0.5时,可以认为该参数能够通过观测反演得到[36].总DFS则描述了观测系统的整体能力,是基于最优化估计反演框架对卫星观测能力总的定量化评价.后验误差又称为理论反演误差,描述了反演结果的不确定性.这两个指标是定量分析卫星传感器对气溶胶遥感观测能力的有力工具,下面给出其定义和具体描述.

卫星观测系统可以用形式简单的前向模型进行描述:

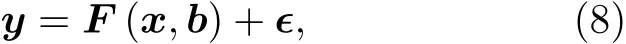
其中,y为观测向量,由卫星传感器观测的强度和偏振辐射量构成;x为状态向量,由待反演的地表和气溶胶参数构成;b为非状态向量,由非反演的地表或气溶胶参数构成;F为描述状态量和观测量之间物理关系的前向模型,即大气辐射传输过程;是经验误差项.假设误差遵循高斯概率分布,基于贝叶斯理论,则反演结果向量可以描述为:

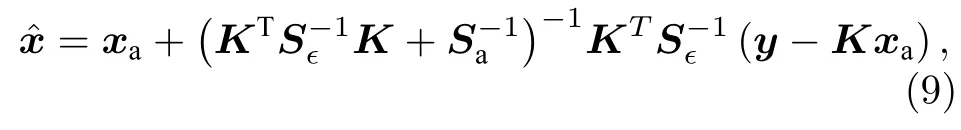
后验估计对状态参数的偏导数称为平均核矩阵,描述了反演结果对真实状态的敏感程度,定义为

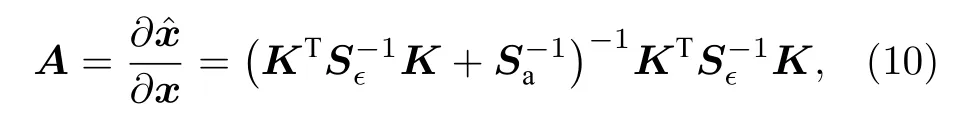
A是归一化的矩阵,对角元素Ai,i即为第i个状态参数的DFS,而观测系统总的DFS是矩阵A的对角元素之和,即矩阵A的迹.

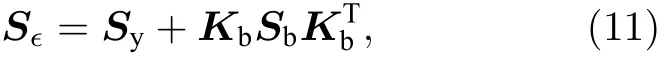
其中Sy描述了传感器的测量误差,主要由卫星传感器的信噪比和定标误差等因素决定;右侧第二项描述了先验误差(气溶胶或地表模型误差)经过前向辐射传输计算后传递到模拟观测的误差,其中Sb为非状态向量误差协方差矩阵,描述了模型参数先验估计的不确定性,Kb为模拟观测对非状态矢量的雅可比矩阵.最终,后验误差协方差矩阵可以表示为:

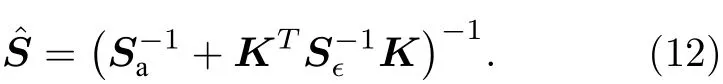
假设每一次测量相互独立,同时模型参数之间是不相关的[37],则 Sy,Sa和 Sb均为对角矩阵,从而对角元素的平方根即为对应参数的后验误差.

4 多角度偏振仿真

4.1 观测几何

图1为基于DPC多角度观测模式提取的四组典型观测几何,每一组观测包含12个观测角度,具体由对应的观测天顶角()和相对方位角()所组成的极坐标来表示,=0°处的实心标识符分别为四组观测对应的太阳天顶角().

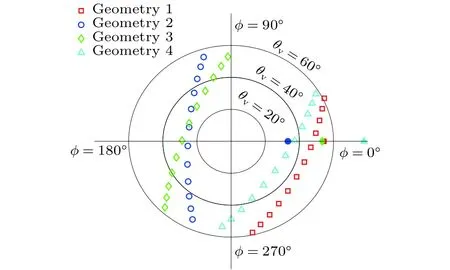
图1 研究采用的 DPC 多角度观测几何Fig.1.Multi-angle observation geometries adopted in the simulation,information content analysis and a posteriori error analysis. The solid circle, diamond, square and triangle with ϕ =0°represent the corresponding position of the Sun for Geometry1−4,respectively.

为了分析观测角度数量对反演的影响,按照观测天顶角由小到大对每一组观测中的12个角度进行排序,然后依次增加观测角度个数,从而形成包含不同观测角度个数的观测模式,具体如图2所示.

对应地,各组观测在不同的观测角度个数下散射角的分布范围如图3所示,其中第2和第3组观测覆盖的散射角范围较小,第1和第4组观测覆盖的散射角范围较大,同时更靠近后向散射区域.四组观测的散射角范围分别为 [116.68°,173.62°],[107.72°,121.62°],[82.23°,109.78°] 和 [92.58°,145.82°].

4.2 观测向量及观测误差

DPC的一组多角度观测数据包含不同观测几何、不同观测波段的强度和偏振观测值:

式中的I和Lp分别为强度和偏振观测构成的向量:

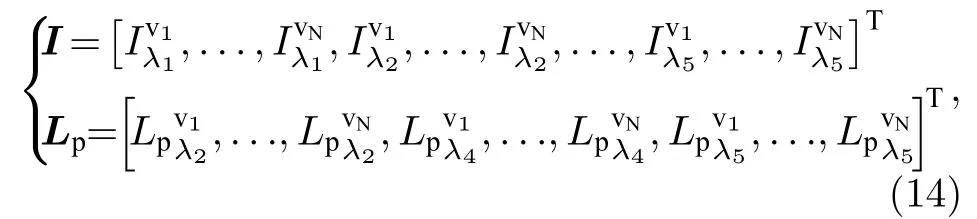
其中,v1—vN分别表示第1到第N个观测角度(N≤12）,λ1—λ5分别对应 DPC 传感器的 443,490,565,670 和 865nm 通道.DPC 具备 12 个角度的观测能力,因此一组观测最多可包含12×(5+3）=96 个观测量.

强度和偏振作为两种不同的观测量,其定标精度也有所不同,因此需要对二者的观测误差分别进行考虑.DPC辐射强度测量的相对不确定性在3%到5%之间,这里按照上限5%设定,即0.05,表示绝对定标误差;对于偏振测量,DPC采用实验室偏振盒定标的方法,表1中的偏振定标精度为线偏振度 (degree of linear polarization,DOLP)的最大绝对误差,为了更准确描述偏振测量误差,用下式来描述线偏振度的不确定性:

图2 不同观测角度个数的观测示意图Fig.2.Illustrationsof observation scenarios with different number of viewing angles.

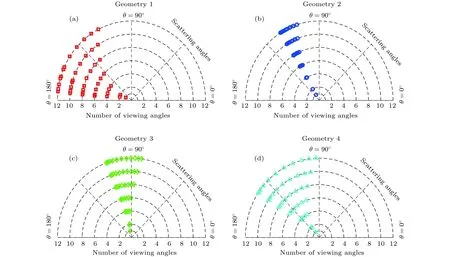
图3 四组观测在不同观测角度个数下的散射角分布Fig.3.Distribution of the range of scattering angle corresponding to the geometries in Fig.1.

其中右边两项分别描述了辐射定标不确定性和偏振定标不确定性.假设观测误差不随波段和观测角度变化,即观测误差与观测模式无关,则Sy可以写成以下形式:

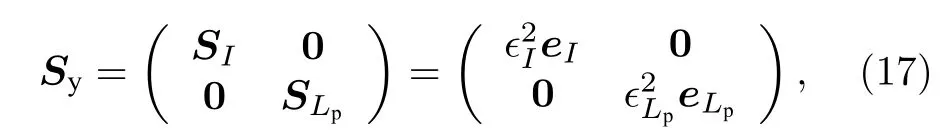
其中,SI和SLp分别表示强度和偏振观测的误差协方差矩阵,eI和 eLp分别表示和 I,Lp具有相同维度的单位对角矩阵.

4.3 气溶胶和地表模型参数及先验估计误差

表2列出了状态向量x和非状态向量b的组成情况,为了分析所有气溶胶和地表参数的可反演性,将信息量分析过程分为两种情况:一是将气溶胶和地表的参数全部视为状态参量,即没有非状态参量;二是将气溶胶的模型参数(包括复折射指数、有效半径和有效方差)视为非状态参量.

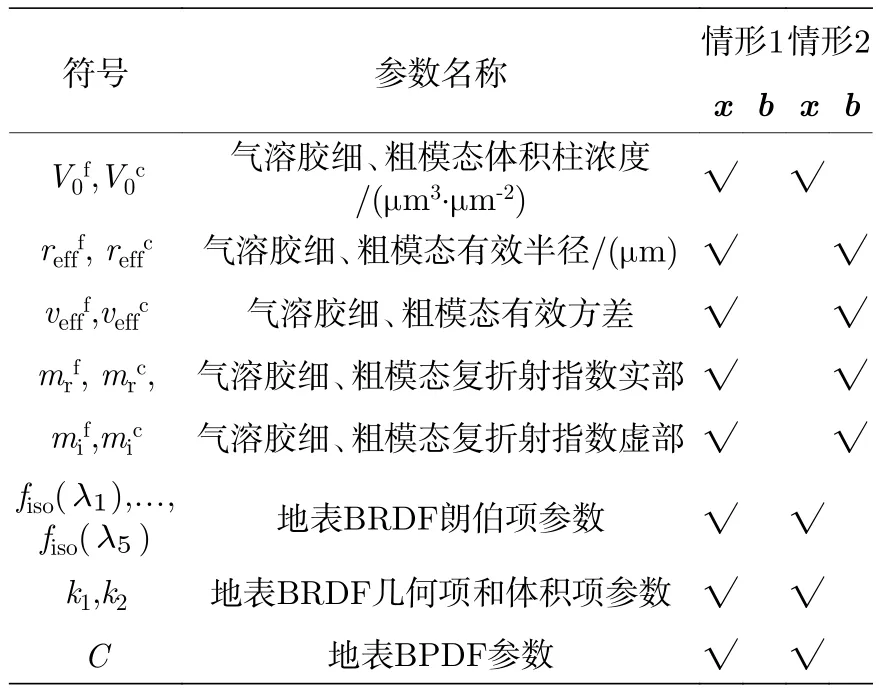
表2 状态向量和非状态向量的参数组成Table2. State vector and non-state vector elements for different scenarios.

误差协方差矩阵Sa和Sb由对应参数的先验估计误差构成,可以描述为:

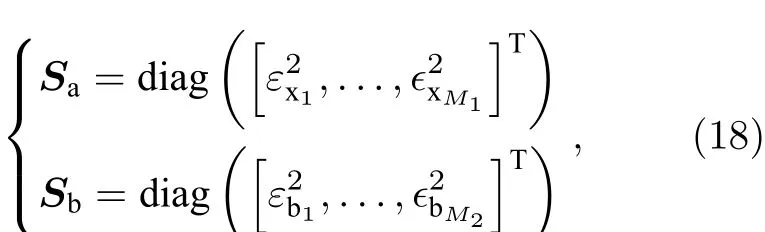
其中diag(…)表示构造一个对角矩阵,由向量元素构成矩阵的主对角元素.M1和M2分别表示反演参数和非反演参数的数量,第一种情况M1和M2分别为18和0,第二种情况M1和M2分别为10和8.

本研究中,气溶胶模型参数采用地基AERONET多年的观测统计数据[38];BRDF参数中,fiso()取自USGS和ASTER的地表反射率数据库[39,40],对应的误差来自基于数据库地表反射率变化范围的统计;k1和 k2参数采用 Litvinov等[35,41]的研究;BPDF参数C来自Maignan等[34]的研究.表3列出了参数的取值及相应的误差,其中,气溶胶mr参数、作为状态量时的mi参数以及地表fiso()参数为绝对误差,其他参数为相对误差.

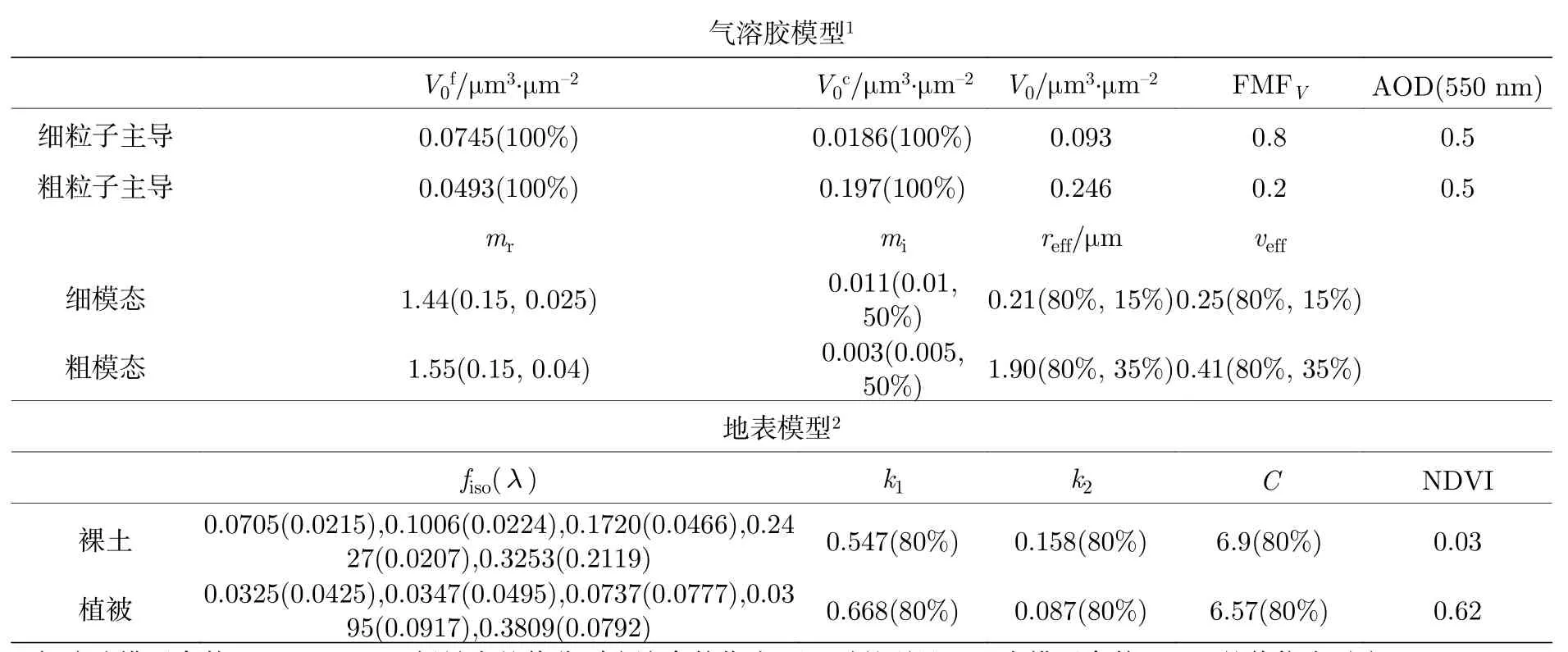
表3 气溶胶和地表模型参数及其先验估计误差Table3. A priori value of the aerosol and surface model parameters and corresponding errors adopted in the simulation.

气溶胶分为细粒子主导(fine-dominated)和粗粒子主导(coarse-dominated)两种典型类型,分别对应城市污染型和沙尘型气溶胶[42,43];地表分为植被和裸土两种类型,分别对应卫星观测中的暗地表和亮地表情况.表2中的气溶胶体积柱浓度对应550nm的AOD为0.5,为轻度污染天气情况.

4.4 卫星观测仿真

根据4.1节中的观测几何,基于4.2和4.3节的模型参数设置,利用UNL-VRTM前向模型对DPC多角度观测进行前向模拟仿真,本节描述了DPC强度和偏振观测的仿真结果以及地表模型误差对TOA观测的影响.

4.4.1 DPC强度观测仿真

Litvinov等[35]的研究表明,改进的BRDF模型误差小于2%,造成TOA总反射率的不确定性为4%—5%,其中裸土地表的不确定性略大于植被地表.在实际的反演中,由于地表的先验知识难以精确获取,很多情况下无法准确判断地表状态,特别是混合像元等情况.因此,在模型误差的基础上,地表先验估计的不确定性也会造成TOA反射率的误差,先验不确定性具体表现为不恰当的模型参数估计.我们基于改进的BRDF模型,通过对参数k1,k2参数引入误差,分析先验估计误差对地表反射率和表观反射率的影响.

图4为模拟的地表反射率(rSurf)和表观反射率(rTOA),以及参数k1参数叠加10%相对误差所引起的 rSurf和 rTOA的误差情况.其中,图 4(a)—(e)和图4(f)—(j)分别对应植被和裸土地表类型在不同波段的结果,每个子图又包含4组观测的对比.模拟采用了细粒子主导的气溶胶类型,AOD550nm=0.2.

由图4可知,1）受到瑞利散射和气溶胶的影响,在 443 和 490nm 波段,表观反射率和地表反射率的差异较大,而在 565,670 和 865nm 波段,表观反射率和地表反射率的差异明显减小.植被和裸土地表表观反射率波段间的特征仍然存在.2）参数k110%的误差会导致平均5.6%的地表反射率的误差,受程辐射的影响,表观反射率的平均误差降至4.65%.表观反射率最大存在6.8%的误差,发生在裸土地表 865nm 波长处.3）误差的传递并未表现出对卫星观测几何较大的依赖,植被地表的不确定性和对应的TOA误差略小于裸土地表,这一点与Litvinov等的研究相一致[35].另外,结合图3可知,较大的表观反射率误差主要发生在散射角变化较大的观测情形(Geometry1和4）.

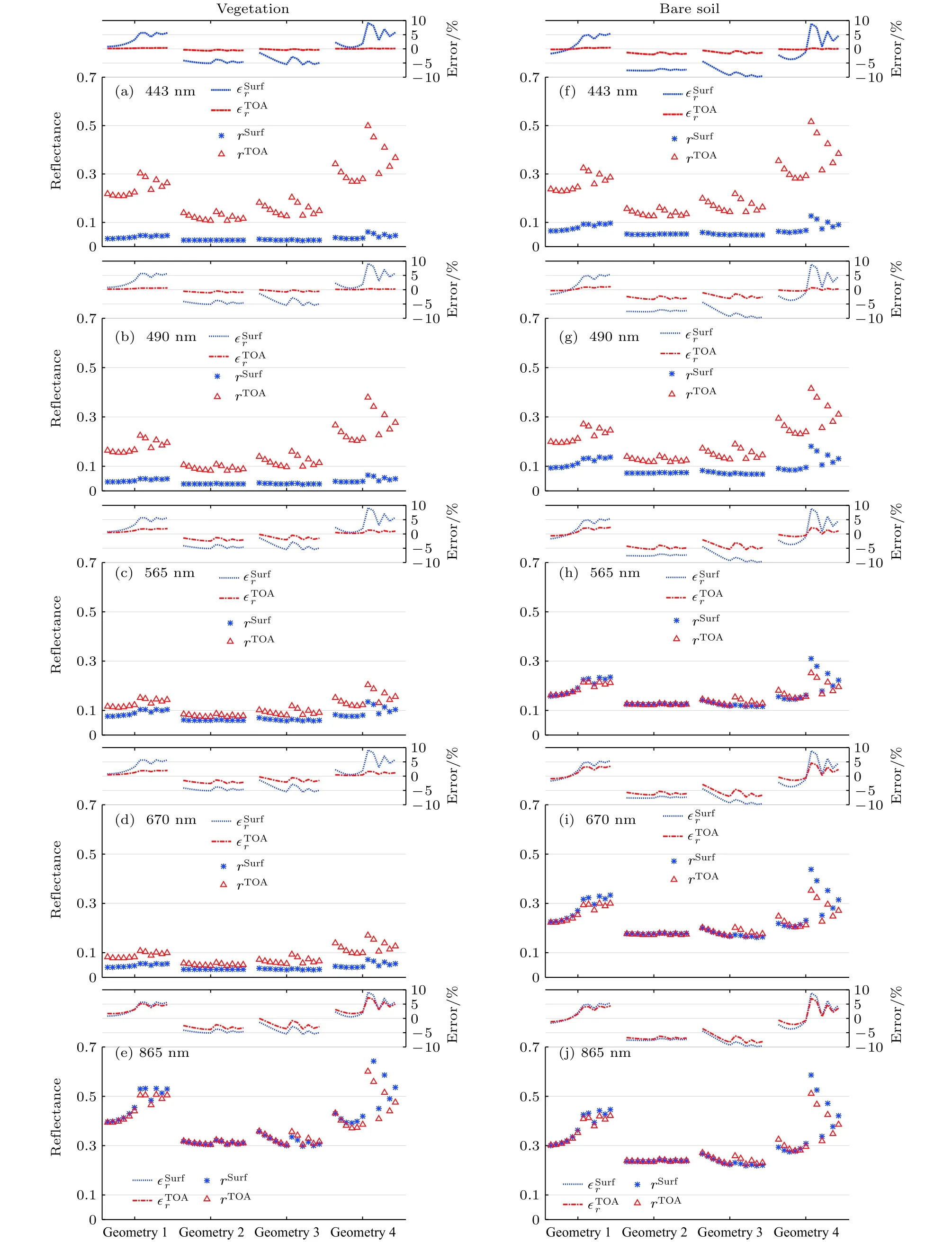
图4不同观测几何下的地表反射率、表观反射率以及地表模型参数误差对表观反射率的影响(a)–(e)植被地表;(f)–(j)裸土地表Fig.4.Contribution of surface reflectance to TOA reflectance at443,490,565,670and865nm,as well as the influence of BRDF parameter error to TOA reflectance for vegetation((a)–(e))and bare soil((f)–(j))surface.The horizontal axis of each case is arranged by scattering angle.

4.4.2 DPC偏振观测仿真

基于BPDF模型进一步模拟了DPC多角度偏振观测.仿真采用细粒子主导气溶胶类型,AOD550nm=0.2.图 5 的下半部分为四组观测几何下植被地表的偏振反射率(rpSurf)及三个偏振波段 (490,670和 865nm)的 表 观 偏 振 反 射 率(rpTOA).图5的上半部分为参数C叠加10%相对误差引起的rpSurf和rpTOA的变化情况.

由图 5可以发现:1）地表偏振反射率对TOA的偏振贡献较小,表观偏振反射率主要来自于气体分子和气溶胶的偏振贡献.同时,偏振反射率对观测几何具有较强的依赖性,不同的观测角度偏振反射率存在较大的差异.2）参数C10%的相对误差会引起地表偏振反射率0.7×10–3的差异,然而这一误差传递到TOA后,会降低2个数量级.490,670和865nm的表观偏振反射率误差分别为 0.54×10–5,0.36×10–5以及 0.33×10–5.

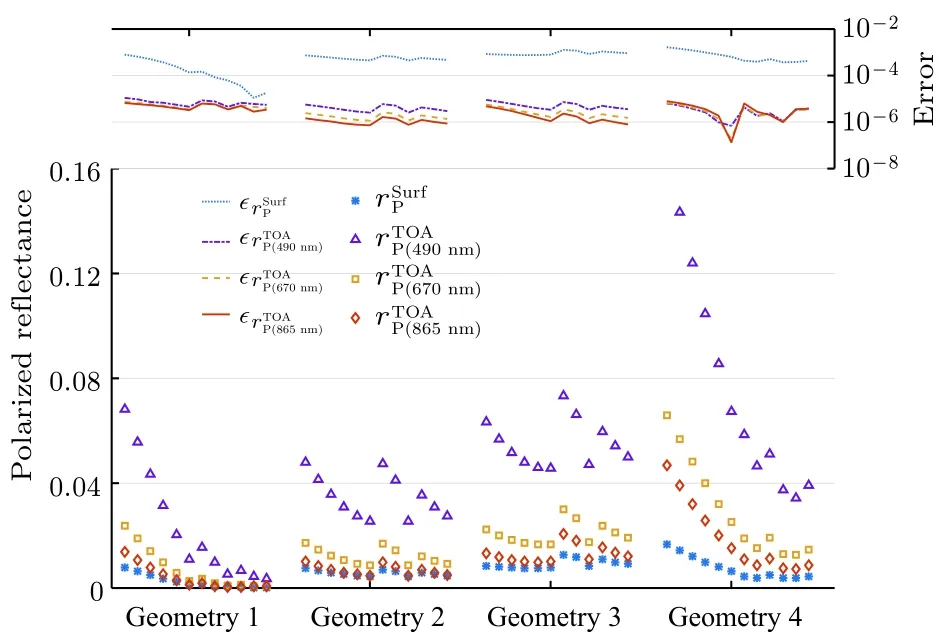
图5 不同观测几何下植被地表偏振反射率和表观偏振反射率,以及10%的参数不确定性对二者的影响Fig.5.Contributionof polarized reflectance to TOA polarized reflectance for vegetation surface at490,670and 865nm,as well as the influence of BPDF parameter error to TOA polarized reflectance.

5 结果与分析

5.1 信息量分析

5.1.1 信息量对观测角度的依赖性

针对不同气溶胶和地表类型,在轻度污染条件下 (AOD550nm=0.5）计算 4.3 节全部参数视为状态参量情况下的DFS.图6采用盒须图的形式给出了总DFS随观测角度个数的变化情况,每个盒须图包含中值(盒中实线)、25%值(盒底),75%值(盒顶)以及数据最大值(须顶)和最小值(须底).由图6可以得到以下结论.

1）总的DFS随观测角度数量的增加显著提升.图 6(a)中,观测角度个数从 1 增加到 12,气溶胶总 DFS增加了 5.9(从 3.3增至 9.2）,地表总DFS增加了2.7(从3.8增至6.5）.根据信息量分析理论,多角度观测比单角度可以额外提供5—6个气溶胶参数和3个地表参数的反演约束.四组观测平均而言,多角度观测信息量比单角度提高了5.45个DFS(从6.75增至12.2）,理论上相当于多反演5—6个参数.这表明多角度观测对气溶胶反演具有重要提升作用.

2）信息量随观测角度数量的增加并非呈现线性增长.图6(d)中,气溶胶信息量前9个角度增加了3.2(从3.0增至6.2）,后3个角度仅增加了0.4;图6(h)中,地表信息量前9个角度增加了3.6,而后3个角度同样仅增加了0.4.这是由于随着观测量的增加,有效观测信息逐渐趋于饱和.

3）多角度观测下,卫星的观测几何不同时,气溶胶信息量呈现较大差异.图6(a)中,气溶胶总DFS 为 9.2,而图 6(b)中,总 DFS 为 4.4,即信息量相差4.8个DFS.由此可见,气溶胶参数反演对卫星的观测几何有很强的依赖性.结合图3可知,卫星观测的散射角覆盖范围越大,对气溶胶反演越有利.相对于气溶胶,地表信息量并未表现出对观测几何较强的依赖,4组观测下地表总DFS的平均差异仅为0.5.这主要是由于地表参数fiso()与观测角度无关,同时,TOA观测对地表偏振相对不敏感,因此,随着观测角度数量的增加,地表信息量的增长主要发生在参数k1和k2上.

总的来说,DPC多角度观测包含的气溶胶信息量平均为6.4个DFS,地表信息量平均为6.2个DFS.因此,理论上DPC多角度测量能够约束超过12个参数的反演.另外,由图6中误差棒的范围可知,相对于地表,气溶胶参数的反演精度更容易受到气溶胶和地表类型的影响.

5.1.2 信息量受气溶胶和地表类型的影响程度

图7给出了多角度观测下各状态参数的信息量情况,其中图7(a)为两种类型气溶胶信息量的对比(采用植被地表);图7(b)为两种地表信息量的对比(采用细粒子主导气溶胶类型),图中各柱子的高度及相应误差棒分别对应四组观测几何的DFS均值和标准差,由图7可以得到以下结论.

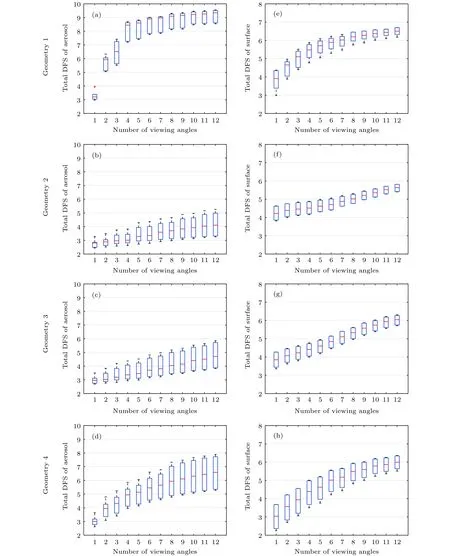
图6 气溶胶和地表参数的总信息量随观测角度数量的变化情况((a)—(d))气溶胶参数;((e)—(h))地表参数Fig.6.The total DFS of aerosol((a)−(d))and surface((e)−(h))parameters as functions of number of viewing angles in terms of surface type(vegetation and bare soil)and aerosol type(fine-dominated and coarse-dominated)with AOD550nm=0.5.Quantities in each box-whisker include the median (dash in the box),the25thand 75thpercentiles(box),and the minimum and maximum(whiskers)for each number of viewing angles bin.

1）气溶胶信息量主要集中在体积柱浓度、复折射指数实部和有效半径三个参数上.V0f,mrf和refff在两种气溶胶类型下的DFS均超过0.9;V0c,mrc和reffc在粗粒子主导类型下的DFS分别为0.8,0.95和 0.9,而在细粒子主导类型下 DFS仅为0.2,0.35和0.4,表明粗模态体积柱浓度的反演与气溶胶类型有关,在细粒子主导类型下反演存在一定困难;其他气溶胶参数中,细粒子主导类型下的和粗粒子主导类型下的的DFS在0.5左右,信息量依赖于观测几何;复折射指数虚部的信息量较少,因此反演难度较大.

3）地表参数误差棒的范围显著小于气溶胶参数,表明地表反演受观测几何影响相对较小,而气溶胶反演更依赖于观测角度;参数k1和k2的DFS误差棒范围高于其他地表参数,表明这两个参数对卫星观测几何的依赖性相对更强.

5.2 后验误差分析

5.2.1 反演参数的后验误差

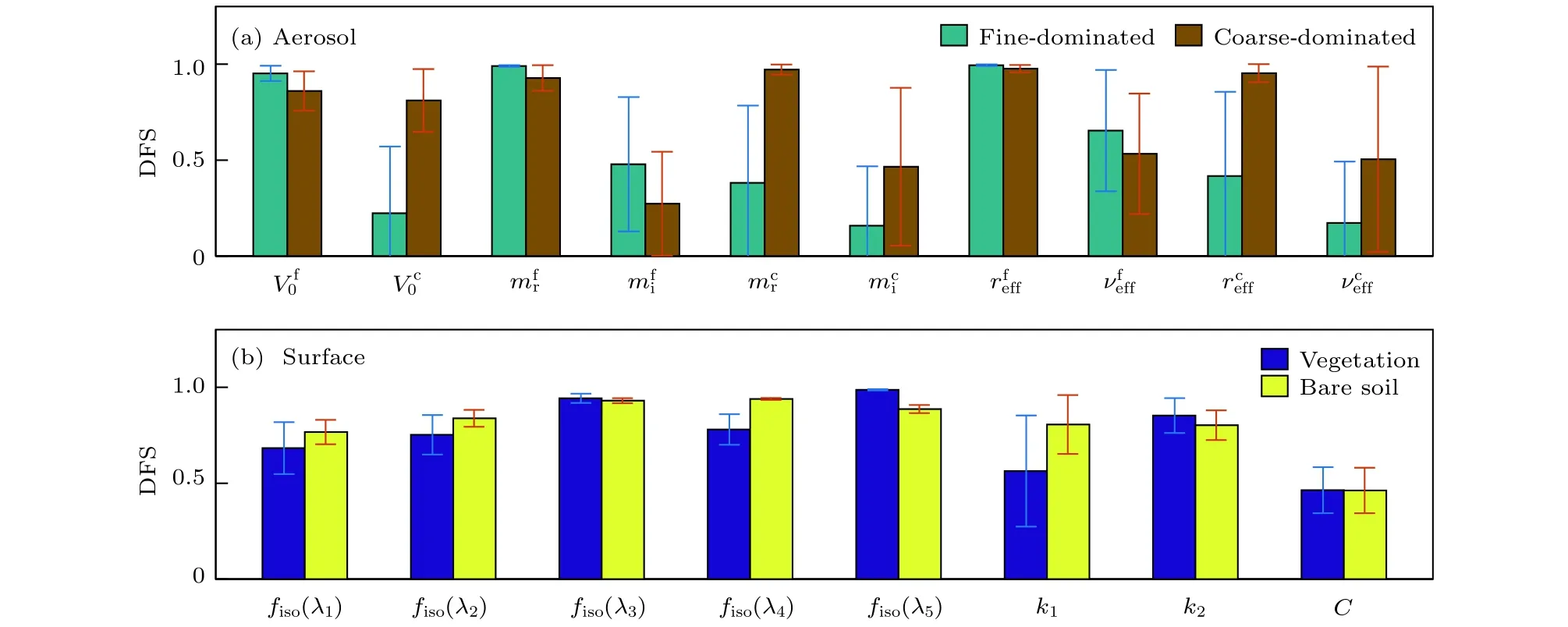
图7 不同观测几何下气溶胶和地表各参数的信息量 (a)气溶胶;(b)地表Fig.7.The DFS of aerosol and surface parameters under condition of12viewing angles(AOD550nm=0.5）:(a)Aerosol;(b)surface.Each histogram and error bar are the mean value and standard deviation of different geometries.

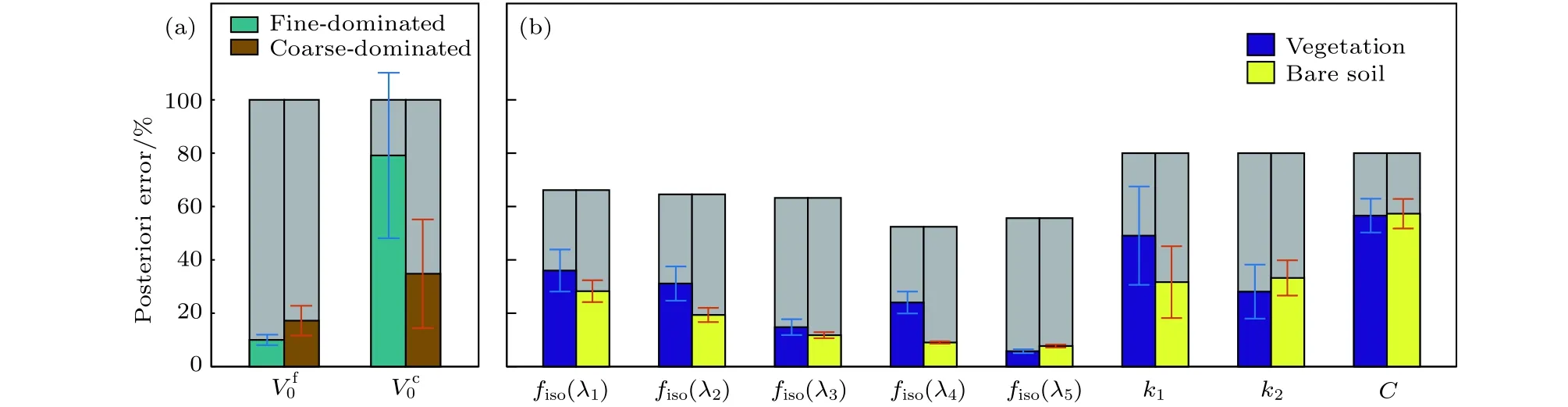
图8 多角度观测下气溶胶和地表参数的后验误差(灰色底柱为先验估计误差)Fig.8.The posteriori error of retrieved aerosol parameters(a)and surface parameters(b).The histogram and error bars are the mean and standard deviation of different geometries(Geometry1−4）.Both(a)and(b)are calculated under condition of12viewing angles(AOD550nm=0.5）.The gray histogram means the priori estimate error.

针对4.3节第二种情况,即气溶胶模型参数作为非反演参数,计算了多角度观测下各状态向量的后验误差.图8(a)为两种气溶胶类型的体积柱浓度后验误差的对比(采用植被地表类型),图8(b)为两种地表类型的地表参数后验误差对比(采用细粒子主导气溶胶类型).图中各柱状图及误差棒分别对应四种观测的均值和标准差,灰色底柱的高度表示参数的先验估计误差,灰色底柱可见部分为后验误差相对先验误差的减少量.

5.2.2 观测角度个数对后验误差的影响

图9给出了气溶胶和地表各参数后验误差随观测角度个数的变化情况,计算采用第1组观测几何,曲线和误差棒分别表示两种地表和气溶胶类型的后验误差的均值和标准差.由图9可以得出以下结论.

1）随着观测角度数量的增加,气溶胶参数的后验误差显著降低,其中的后验误差从34.3%降至8.8%,的后验误差从78.3%降至20.7%;地表参数k1和k2的后验误差分别从80%和70%降至 30%和 25%,降低同样非常明显;然而,的后验误差随着观测角度个数的增加并未出现显著的下降,表明该参数的反演对观测角度的个数并不敏感;参数C的后验误差仅从60%降至50%,表明观测对参数C的敏感性仍显不足.

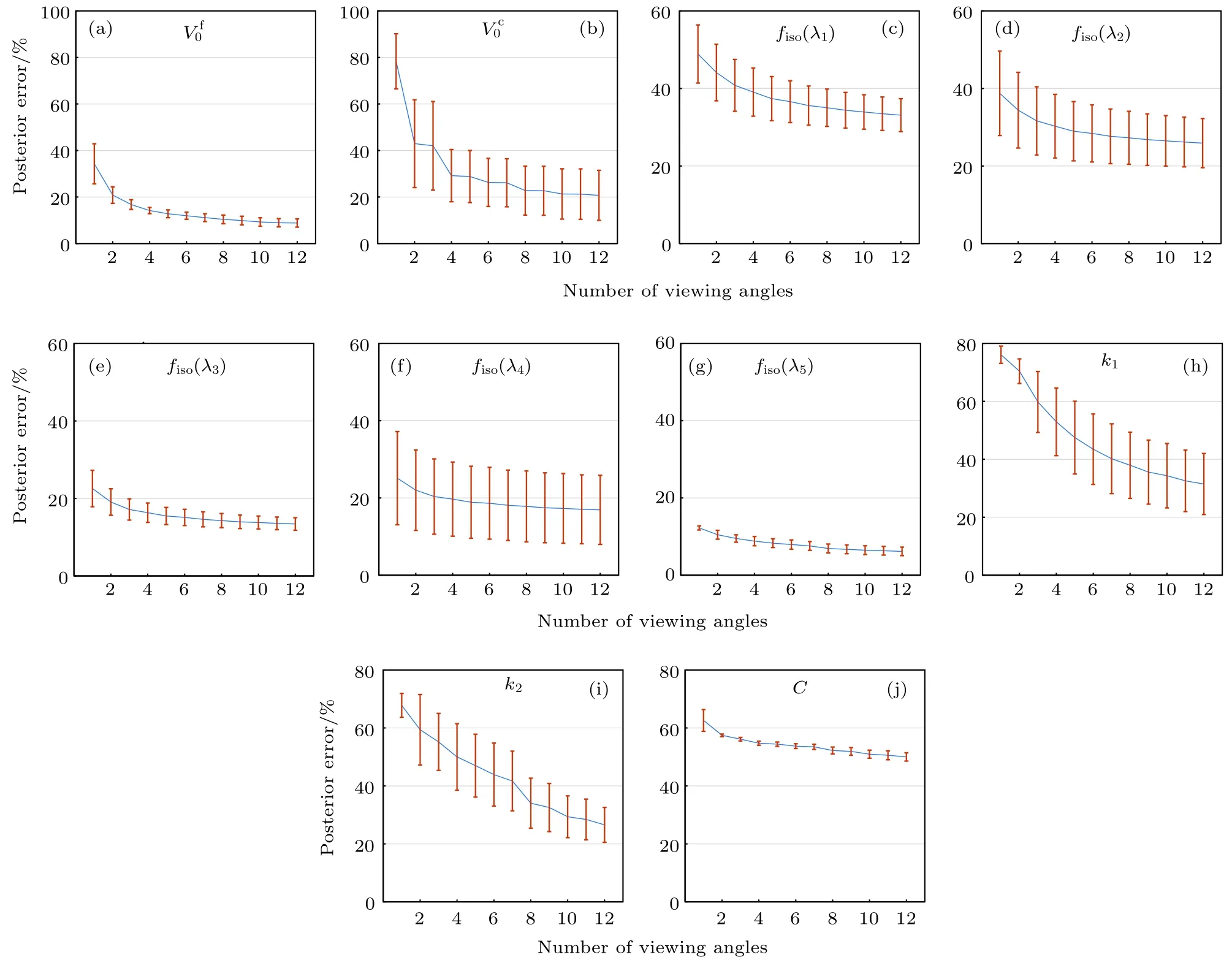
图9 地表和气溶胶参数的后验误差随观测角度数量的变化情况Fig.9.The posteriori error of retrieved aerosol and surface parameters as a function of number of viewing angles(AOD550nm=0.5）.The curve and the error bar are the mean value and standard deviation of different aerosol and surface type,respectively.

5.2.3 观测不确定性对后验误差的影响

图10给出了气溶胶和地表参数的后验误差随观测误差的变化情况,计算采用第1组观测几何,并考虑了总的观测误差变化和仅偏振观测误差变化两种情况,分别如图中的实线和虚线所示.图中的曲线和相应的误差棒分别表示两种地表和气溶胶类型的后验误差的均值和标准差.由图10可以看出,气溶胶的后验误差随观测误差的增加从1%增至11.6%,基本和观测误差的变化一致,略高于观测误差;的后验误差从3.2%增至24.4%;443,490 和 670nm 波段的受观测误差影响非常显著,而565和865nm波段受影响相对较小;k1和 k2后验误差分别从3.9%,3.6%增至 41.1%和33.7%;地表BPDF模型参数C从12.2%增至53.3%.另外,由误差棒范围可知,,565 和 870nm波段的以及参数C受地表类型和气溶胶类型的影响较小.由图10中的虚线可以看出,偏振测量误差主要影响的是气溶胶参数的反演精度,气溶胶的后验误差随观测误差的增加分别从1%,3.2%增至8.56%和16.66%,而偏振观测误差变化对地表参数反演的影响较小.

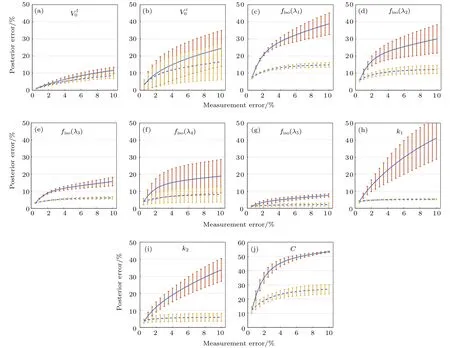
图10 地表和气溶胶参数的后验误差随观测误差的变化情况Fig.10.The posteriori error of retrieved aerosol and surface parameters as a function of measurement error(AOD550nm=0.5）.The solid line and the error bar are the mean value and standard deviation of different aerosol and surface type,respectively.The dash line denotes the contribution from polarized observation error.

5.2.4 气溶胶模型不确定性对后验误差的影响

卫星气溶胶反演算法需要基于一定的先验知识,例如,AOD 反演需要假定气溶胶类型.然而,先验知识往往存在一定的误差.4.3节假设气溶胶模型参数已知(包括气溶胶复折射指数和粒子谱分布参数),并给出了相应的不确定性,本节分析后验误差随气溶胶模型参数估计误差的变化情况,结果如图11所示.计算中,气溶胶模型参数误差从1%到100%变化.由图11可知,随着模型参数误差的增大,气溶胶V0c的后验误差从15%增至40%,是受气溶胶模型参数不确定性影响最大的参数;地表参数后验误差受气溶胶模型参数不确定性的影响较小,其中参数k1和k2受影响相对较大一些,后验误差分别从35%和15%增至40%和25%.

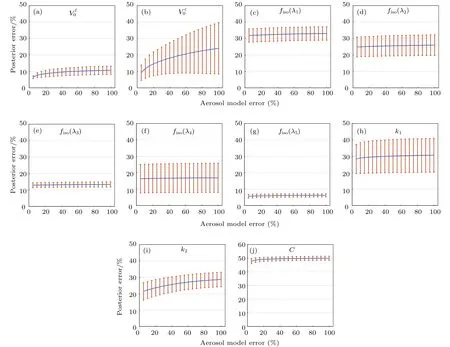
图11 地表和气溶胶参数的后验误差随气溶胶模型误差的变化情况Fig.11.The a posteriori error of retrieved aerosol and surface parameters as a function of aerosol model error(AOD550nm=0.5）.The curve and the error bar are the mean value and standard deviation of different aerosol and surface type,respectively.

6 结 论

本文针对DPC气溶胶反演需求,基于多参数最优化估计反演框架,模拟了DPC多角度偏振观测,分析了观测信息量对观测角度数量和观测几何的依赖性,给出了气溶胶和地表参数后验误差以及后验误差随观测角度个数、观测误差和气溶胶模型误差的变化情况,通过引入信息量和后验误差分析工具,定量化系统评估了DPC陆地气溶胶反演能力,为DPC在轨测试、反演算法的发展以及后续卫星传感器的设计提供参考.得到以下主要结论.

1）卫星观测信息量随观测角度个数的增加显著提升,气溶胶参数后验误差随着观测角度个数的增加显著降低.观测角度个数从1增加到12,气溶胶和地表总DFS平均提高了5.45(从6.75增至12.2）,气溶胶V0f和V0c的后验误差分别降低了86.4%和57.6%,表明DPC多角度观测对气溶胶反演具有重要提升作用.

2）气溶胶反演表现出对卫星观测几何较强的依赖性.相同观测角度个数下,不同观测几何会引起气溶胶信息量4—5个DFS的差异,散射角覆盖范围越宽,观测包含的信息量就越多.

3）多角度观测下,气溶胶体积柱浓度、复折射指数实部和有效半径参数的信息量较高,具有较好的可反演性.其中,在两种气溶胶类型下平均 DFS 均大于 0.9;在粗粒子主导类型下平均DFS均大于0.8,而在细粒子主导气溶胶类型下平均DFS均低于0.5,表明粗模态气溶胶反演存在一定的不确定性.

4）影响气溶胶参数反演误差的因素中,气溶胶模型不确定性对后验误差的影响并不显著,而观测不确定性是影响后验误差的主要因素.当观测误差从5%增加到10%,气溶胶后验误差将分别增加4.15%和7.44%.