用光晶格模拟狄拉克、外尔和麦克斯韦方程*

朱燕清 张丹伟 朱诗亮 2）‡

1）(南京大学物理学院,固体微结构国家实验室,南京 210093）

2）(华南师范大学物理与电信工程学院,广东省量子调控工程与材料重点实验室,广州 510006）

相对论性量子力学波动方程,如狄拉克、外尔和麦克斯韦方程,是描述微观粒子运动的基石.最近的实验和理论研究表明,冷原子系统中几乎所有参数都可精确调控,因此冷原子系统被认为是实现量子模拟的理想平台,可以用来研究高能和凝聚态物理中的一些基本问题.本文介绍了设计原子光晶格哈密顿量的思路和方法,主要涉及激光辅助跳跃的理论.基于这些方法,物理学界提出了利用光晶格体系模拟相对论性量子力学波动方程,包括狄拉克、外尔和麦克斯韦方程等,并且预言了一些在基本粒子物理中很难观察到,但在冷原子体系可能观察到的物理现象.本文综述了国际上此领域的研究进展.

1 引 言

自上个世纪80年代以来,伴随着超冷原子系统中实验技术的日臻成熟,例如超冷原子气体制备[1−5]、原子间相互作用的调控[6]、光晶格[7]和人工规范场的产生[8−10]等,科学家对于冷原子系统的操控已取得令人瞩目的成就.最近的理论和实验研究都证明,超冷原子体系可用于模拟和研究凝聚态和高能物理中的一些重要模型[11],特别是可以模拟一些很难实验实现的模型或理论上很难处理的体系或物理现象,例如量子相变、高温超导、量子磁阻挫、极端条件下的相对论性粒子等.冷原子量子模拟的突出优点是,绝大部分相关的物理参数在实验上都能够精确调控,从而可以人为设计和实现所需要的哈密顿量.

另一方面,相对论性量子力学波动方程,如狄拉克、外尔和麦克斯韦方程,是描述微观相对论性粒子运动的基石.并且有些很早就预言的现象,如薛定鄂预言的狄拉克粒子的Zitterbewegung振荡等,一直没有在基本粒子中观察到.如何在冷原子体系中模拟这些相对论性波动方程,并且观察到之前不能观察的极端条件的物理现象,正成为冷原子量子模拟的一个重要研究方向.相对论性波动方程中,哈密顿量是动量的一次方,而描写冷原子的原始哈密顿量一般是动量的二次方.如何消除动量的二次方,突出一次方的效应,是此类量子模拟的关键.在现有的理论中,有两种方式可以做到此点:1）基于诱导规范势的方法,利用激光对有内部能级结构的原子产生几何相位,可以实现自旋相关的等效规范势,从而可实现类似的哈密顿量,其中为原子的动能项.在超冷原子中,原子动量可以很小,上述哈密顿量中,在某些情况下第一项远小于第二项,从而得到相对论性方程需要的线性色散关系[12].2）由于晶格中的某些对称性,在动量空间中,一些点附近是线性色散关系,从而描写具有这些准动量的粒子需要相对论性方程.类比凝聚态系统中电子在固体周期势场和外加电磁场中的运动[13],将冷原子放置在由激光形成的光晶格中,辅以适当的激光调制以实现人工规范场,如激光辅助跳跃[14,15]、周期调制光晶格[16]等技术,可以实现有线性色散关系的格点哈密顿量.这两个方式都可以用于模拟相对论性粒子及其物理效应.本文着重介绍利用光晶格体系实现相对论性量子力学波动方程的研究.该量子模拟的关键在于设计合适的光晶格和激光调制,使得超冷原子在能带中某些特定点附近的低能激发满足相应的相对论波动方程.本文首先概述激光辅助跳跃和光晶格紧束缚哈密顿量的基本理论,然后分别介绍在光晶格系统中实现狄拉克、外尔和麦克斯韦方程的几个具体方案,最后是总结和展望.

2 原子哈密顿量的设计

2.1 激光辅助跳跃

激光辅助跳跃的基本思路是:首先抑制原子在近邻格点的自然跳跃(如光晶格势阱较深或近邻格点的能量差较大),然后通过外加拉曼激光耦合近邻格点中的原子来恢复和调控原子跳跃,进而产生等效规范势和自旋轨道耦合[8,9].这里主要介绍文献[15]中利用激光辅助跳跃产生规范势的方案.如图1所示,为实现自旋依赖的光晶格,可考虑在方向施加波长处于“反魔数”(“anti-magic”)波段的驻波场,同时在方向施加处于“魔数”波段的驻波,处在两个不同内态和的原子在平面内感受到的光晶格势为

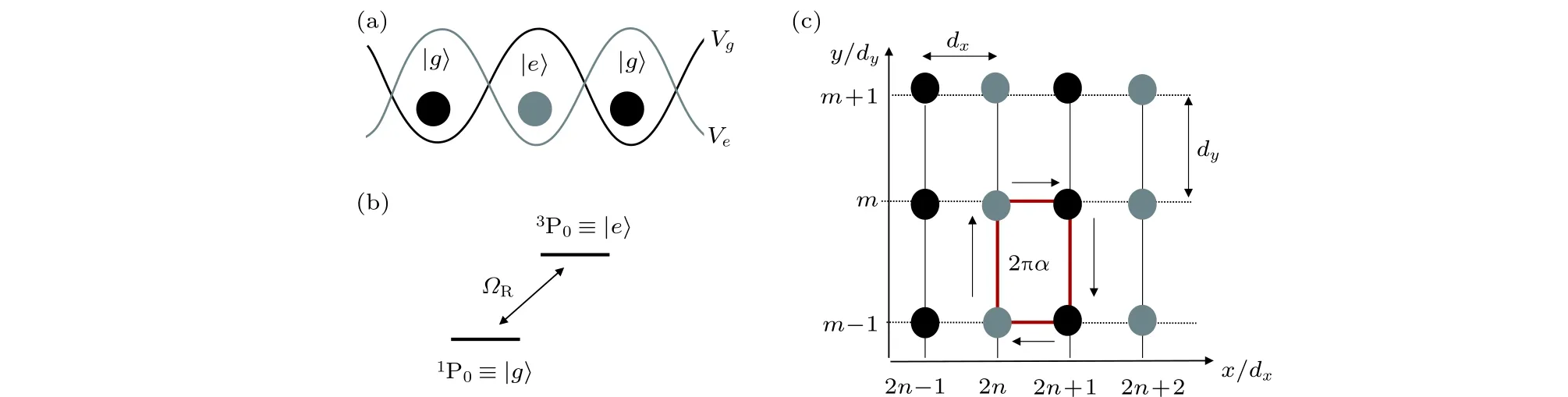
图1 基于激光辅助跳跃实现人工磁场,黑 (灰)色圆分别表示内态为 的Yb原子(a)内态被标记为 和 的原子被囚禁在自旋依赖的光晶格势 和 中,其中 ;(b) 方向上的激光辅助跃迁;(c) 自旋依赖光晶格示意图. 方向存在自然跳跃, 方向由一束拉曼光 诱导跳跃Fig.1.Realization of artificial magnetic field based on laser-assisted tunneling.Gray and black dots represent the Yb atoms correspond to internal states and ,respectively:(a)The atoms and are trapped in the state-dependent optical lattice potentials and ,where ;(b)laser-assisted tunneling along direction;(c)sketch of state-dependent optical lattice.Nature tunneling occurs along the direction,and the tunneling along direction is induced by a Raman beam .

2.2 紧束缚哈密顿量

当晶格势阱足够深,描述光晶格中粒子的有效模型是紧束缚近似下的格点哈密顿量.此时囚禁在势阱中的原子可由局域的瓦尼尔函数描述.假设光晶格中原子一直处于布洛赫能带的最低带上,则原子哈密顿量(1）式的二次量子化形式为

3 六角光晶格和交错磁通光晶格中狄拉克方程的实现

1928年,英国物理学家狄拉克提出了著名的狄拉克方程,即描述自旋粒子的相对论波动方程,其形式为

这里首先回顾一下由Zhu等[18]最早在二维蜂巢光晶格中模拟狄拉克方程的理论方案.考虑将单分量费米原子(如，等)囚禁在蜂巢光晶格中,该晶格可由三束驻波激光照射原子团形成,其势场为

Zhang等[19]提出另一个实现狄拉克方程的理论方案:在自旋依赖的正方光晶格中,通过两束拉曼光耦合两分量的费米原子,以形成一个交错磁通的晶格,此时系统的有效哈密顿量也是二维狄拉克哈密顿量.考虑处于自旋依赖呈棋盘状的正方晶格中的二分量费米气,如图2(a)所示.该晶格在实验上可通过叠加存在偏振夹角的两束线偏振激光产生,其中两个子格(A和B)间的距离以及势阱的深度都可通过调节激光的强度和夹角大小很好

图2 (a)交错磁通光晶格;(b)双光子拉曼过程;(c)等效磁通Fig.2.(a) Staggered flux optical lattice;(b) two-photon Raman process;(c)effective flux.

2012年,苏黎世联邦理工学院的Tarruell等[26]报道了在蜂巢光晶格中使用超冷原子实现具有可调节性质的狄拉克点的实验,他们利用三束回归反射的激光作用在原子团上,通过调节激光间的相对强度实现了与蜂巢晶格拓扑等价的砖墙晶格.狄拉克费米子的探测则通过测量狄拉克点附近的能带色散来实现,能带结构可以通过布洛赫-朗道-齐纳震荡的技术[26−28]进行探测.实验中通过改变激光之间的失谐量,可在子格间产生能量差并导致在狄拉克点打开能隙,而从最低能带隧穿到上一能带的概率随着的变化而改变.当时,即能隙在狄拉克点闭合,隧穿的概率最大,对应上能带的原子布局数最大.随着从0开始变大,对应的隧穿率变小,标志着系统从存在无质量狄拉克粒子到有质量狄拉克粒子的过程.此外,当时,布里渊区中狄拉克点的位置以及相关线性色散的斜率可通过调节激光强度来改变.如文献[18]所述,调节激光间的相对强度,可使得布里渊区中两个拓扑不等价的狄拉克点位置发生移动,当这两个狄拉克点在布里渊区的角落相遇时会相互融合然后湮灭,能隙打开.依据这一原理,就可将发生拓扑相变的临界线描绘出来.而对于狄拉克点对应非零的贝里相,则可以通过原子干涉仪进行探测[29].

三维的狄拉克方程所需的狄拉克矩阵为四个,故不再是泡利矩阵,而是的矩阵,此时的狄拉克哈密顿量在外尔表象下写作

4 三维光晶格中外尔方程的实现

无质量的狄拉克方程(8）式在外尔表象下可写成

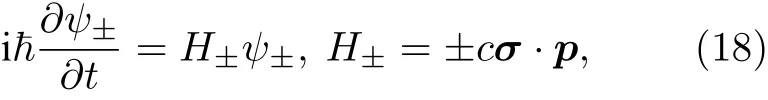
冷原子光晶格系统中实现外尔半金属的理论方案已有许多,如在二维光晶格中引入自旋轨道耦合,再加一个人工维度可以实现外尔半金属[36];通过在两个人工维度中堆垛一维双势阱晶格的拓扑相,或者是直接将二维的具有交错磁通棋盘结构或蜂巢光晶格堆垛成三维的晶格[37−40],都可以实现外尔半金属[37].在这些方案中,自旋自由度可选择用两个原子内态或者两个子格子,对应所需要实现的跳跃项需用到人工自旋轨道耦合和人工磁场.文献[41]给出了通过堆垛Hofstadter-Harper系统成为一个立方晶格以实现拓扑外尔半金属相的方案.图3中展示的是沿和方向存在激光辅助跳跃的三维晶格示意图.为实现这样的跳跃,应先通过在每个格点引入足够大线性倾斜以抑制这两个方斜可以通过在方向引入线性的势场(如重力场、磁场等)产生.正如在2.1节中介绍的方法,引入两束远失谐频率和动量分别相差和的拉曼光可重新诱导这两个方向发生共振跳跃[15,16].该三维晶格对应的有效哈密顿量为

图3 实现外尔半金属的三维立方晶格示意图.合理设计 和 方向跳跃,在动量空间会出现外尔点.虚线和实线分别表示获得相位 和0[41]Fig.3.Schematic diagram of a three-dimensional cubic lattice of a Weyl semimetal.The Weyl points will be created in the momentum space if the tunneling alongand directions are well-designed.The dashed and solid lines indicate the phase and0,respectively.

除了使用与测量二维狄拉克点类似的方法可以探测三维的外尔点之外,另一种观测外尔点的方法是布拉格光谱法:采用额外的一对拉曼光耦合外尔哈密顿量,将下能带的原子激发至上能带用以探测能带结构.该方案将揭示具有非常高分辨率的外尔点的存在,因为它不会改变内部原子态,因此对塞曼位移并不敏感.获得外尔半金属相后,可进一步研究其独特的拓扑表面态,即连接两个手性相反的外尔点的费米弧.外加与一对手性相反的外尔点平行的人工电磁场,系统因手征反常将会出现负磁阻效应,其对应的输运性质也是一个热门的研究课题[39].此外,在标准的线性色散的外尔哈密顿量上增加某一方向的线性项,可获得第二类的外尔点,在费米能级附近的激发同时包含电子和空穴型的激发[42−44].文献[42]中提出的方案可实现一类和二类的外尔半金属以及两者间的Lifshitz型拓扑相变.

5 光晶格中麦克斯韦方程的实现

介质中无源无流的麦克斯韦方程可写为

下面简要介绍文献[45]中的第一种方案.首先考虑实现的二维晶格哈密顿量为

该模型同样可以推广到三维,此时哈密顿量为

6 总结与展望

本文介绍了利用光晶格实现相对论性量子力学波动方程的几个具体方案,并讨论了相应的独特性质和所用到的相关测量方法.这套方法和思路可以用于实现和研究更高自旋的相对论性波动方程[47,48],以及最近引起广泛研究兴趣的可用于拓扑量子计算的阿贝尔或非阿贝尔任意子,如马约纳拉(Majorana)费米子、斐波纳吉(Fibonacci)任意子、仲费米子 (parafermions)等[49−53].此外,赝自旋1的拓扑麦克斯韦费米子有非常丰富的物理性质,值得更进一步研究.类似于狄拉克和外尔费米子,可以讨论麦克斯韦粒子的克莱因隧穿效应[54,55]和 Zitterbewegung振荡[56]动力学,以及非常规的输运特性[57]等.例如,在狄拉克和外尔费米子的Zitterbewegung效应中存在一个振荡频率,但在麦克斯韦费米子的Zitterbewegung振荡中有两种不同的振荡频率[58].此外可将二维模型推广到时间反演的体系,用于模拟光的量子自旋霍尔效应[59].光晶格中的超冷原子因具有高度可控性[60],目前已经成为了模拟凝聚态系统的一个强有力的工具和平台,并且已经取得了一些值得庆贺的成绩,如 Su-Schrieffer-Heeger[61],Bose-Hubbard[62,63],Haldane[64],Hofstadter-Harper[24,25,65]模 型 等 ,这些模型在凝聚态系统中难以实现,但已经在冷原子光晶格系统中被实验实现[11].未来,冷原子光晶格系统将继续用于模拟和研究量子多体系统、拓扑量子物质、高能、天体、甚至是量子信息等领域的问题[66,67].由于具有独特而有趣的物理性质,超冷原子物理必将在各个领域的研究和实现上大放异彩.