光晶格中超冷原子系统的磁激发*

赵兴东 张莹莹 刘伍明

1）(河南师范大学物理与材料科学学院,新乡 453007）

2）(中国科学院物理研究所,北京凝聚态物理国家研究中心,北京 100190)

囚禁在光学晶格中的旋量凝聚体由于其长的相干性和可调控性,使其成为时下热点的多比特量子计算的潜在候选载体,清楚地了解该体系的自旋和磁性的产生和调控就显得尤为重要.本文主要从理论上回顾了光晶格原子自旋链的磁性的由来和操控手段.从激光冷却原子出发,制备旋量玻色-爱因斯坦凝聚体,并装载进光晶格,最后实现原子自旋链,对整个过程的理论研究进行了综述;就如何产生和操控自旋激发进行了详细探讨,其中包括磁孤子的制备;讨论了如何将原子自旋链应用于量子模拟.对光学晶格中的磁激发研究将会对其在冷原子物理、凝聚态物理、量子信息等各方向的应用起指导性作用.

1 引 言

近年来,在光晶格系统中观测到了很多有趣的物理学现象,比如超流-绝缘相变、Landauzener隧穿、布洛赫振荡、孤子等[1−5],囚禁在光学晶格中的玻色-爱因斯坦凝聚体(BEC)很快成为了冷原子物理和多体物理的研究热点之一.其主要原因有二:第一,光学晶格不存在任何杂质和缺陷,这个优点是很多固体系统无法企及的,它为我们搞清楚诸如量子微粒(如冷原子等)在势阱之间如何进行量子隧穿,噪声和耗散是如何影响原子在势阱之间的量子运输以及量子和经典场是如何关联等问题提供了理想而又丰富的环境,同时光晶格中的超冷原子系综为模拟传统凝聚体物理和固体物理中的复杂物理问题提供了一个理想模型;第二,光学晶格中的超冷原子系综极易被操控,目前为止已经有大量的实验和理论工作对如何操控光晶格中超冷原子系综的动力学性质进行了研究,相对于难以调控的固体材料中的交换相互作用,利用原子与磁或光的相互作用可以更方便地实现对晶格中原子相互作用和晶格间的交互作用的调节.

伴随着实验技术的发展,自旋畴和其中的量子隧穿以及自旋交换动力学相继在光晶格系统中被观测到[6,7],这引发了人们对囚禁在光阱中的带有自旋自由度的BEC产生了极大的兴趣[8−14].在晶格势阱很深的条件下,光晶格中的旋量BEC通过量子相变而处于莫特绝缘态,此时整个体系可以看成是一个相干的原子自旋链.此时,各个晶格格点上的旋量BEC就像一个自旋磁子.这些自旋磁子能够通过光诱导的和静磁的偶极-偶极相互作用进行耦合.从这个意义上来说,这样的旋量BEC的原子自旋链和固体物理磁性系统中的自旋链有着一定的相似性.当然,它们也有着明显的差别.在固体自旋链中,由于格点间自旋耦合是短程海森伯交换相互作用所导致,理论模型和处理方法都采用近邻相互作用近似,长程相互作用通常被忽略.在光晶格旋量BEC的原子自旋链里,长程相互作用是非常重要的,而且自旋耦合的强弱可以通过外部光场来控制.近年来,一些与自旋相关的现象如自旋混合、自旋结构的形成、自发磁化的产生、自旋波的激发、磁孤子、宏观自旋隧穿等的物理机理得到了详细研究[1,6,8].由于晶格中原子之间长程偶极相互作用的存在,光晶格超冷原子系综为研究格点系统中更为丰富的自旋耦合动力学特性提供了一个理想的工具,也为超冷原子向量子信息科学与凝聚态物理交叉领域的发展开辟了广阔的前景.

2 激光冷却与玻色-爱因斯坦凝聚

当激光的频率与原子的固有频率相同时,激光射向运动着的原子,原子就会共振吸收迎面射来的光子从低能级跃迁到高能级(图1(a)),由于整个过程动量守恒,原子在得到光子以后的动量等于原子的初始动量和光子动量的矢量和,由于二者反号,被激发的原子的动量就会变小(图1(b)).同时处于激发态的原子会自发辐射出光子而回到低能级的初态并获得反冲动量,因为自发辐射出的光子的方向是随机的,所以多次自发辐射的平均结果并不会增加原子的动量(图1(c)).所谓激光冷却,实际上就是通过激光与原子的作用下使原子减速,温度是物体分子热运动的平均动能的标志,从微观角度看,原子减速了,温度也就降低了.

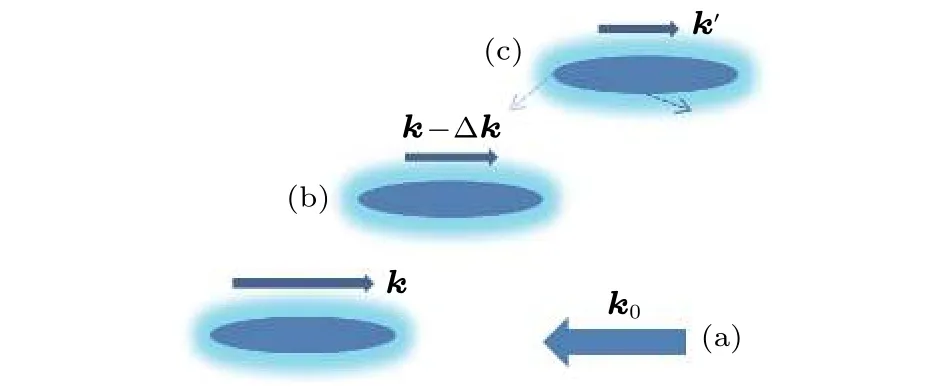
图1 (a)运动的原子和反向传输的激光;(b)吸收光子动量减少的原子;(c)原子随机辐射光子Fig.1.(a) Moving atoms and counter propagating laser;(b) atoms with reduced momentum after absorbing photons;(c)atoms radiate photons in random directions.

激光冷却原子技术可以分为:多普勒冷却、偏振梯度冷却、亚反冲冷却等.激光冷却技术可以将原子冷却到几十的量级,如果要得到更低的温度以实现BEC,还需要其他的冷却技术,如射频蒸发冷却等.射频蒸发冷却技术可以将原子冷却到的量级,此时BEC就可以形成.当温度低于一个临界温度时,理想玻色气体会在最低的能态上突然凝聚,这一物理现象现在被称为BEC,这个现象可以在粒子间没有相互作用时发生,它是全同玻色子体系波函数对称性的结果.对于BEC而言,具有实际意义的情况是原子被外势场束缚且原子间存在相互作用的情况,这也是我们着重讨论的内容.束缚在外势阱中的个相互作用的玻色子的多体哈密顿量的二次量子化形式为:

3 光晶格技术

简言之,相对传输的几对激光束的干涉能在空间形成明暗相间的周期分布,这种周期性场强分布通过与中性原子的偶极相互作用,形成一种控制质心运动的周期性网状势场,这种由激光束干涉而形成的原子偶极势网就是光晶格.激光束中的原子受到的两种力:偶极力和散射力.偶极力使原子陷在晶格中,而散射力则帮助原子冷却,第2节我们已经解释了散射力的原理.

偶极力可以理解为:将非平面波看成是不同模的光波的叠加,原子在这种光场中同时与许多模的光子发生相互作用,它可以从某一模式吸收光子,而在受激发射时发出另一模式的光子.由于不同模式的光子动量不同,在这一过程中虽然吸收和发射光子的能量相同,但动量却有变化.这一动量转移靠原子动量变化来补偿,从而使原子受力.这一过程与相干的受激跃迁有关,其结果是光子在不同模间转移,所以此力也称为感应力.根据半经典理论可得偶极力的表达式为其中是自发辐射率(上能级宽度),即单位时间内原子的吸收率,是跃迁机率,为光强,为激光的失谐.很明显,此力与光强梯度成正比,所以又称为梯度力.当失谐为红失谐时(),力指向方向,即光强最强处;而当失谐为蓝失谐时,力的方向指向光强最弱处.也就是说,当激光频率调谐到低于原子共振频率时,该力就把原子拉向电场最强的地方,如图2(a);而当激光调谐到高于共振频率时,该力又把原子推向电场最弱的的区域,如图 2(b).总之,偶极力可以把原子囚禁在光晶格中.

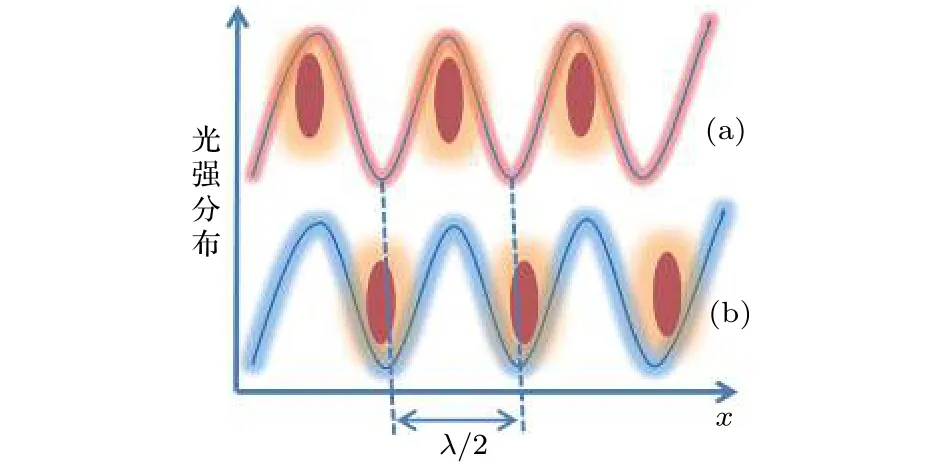
图2 偶极力捕获原子示意图(a) 红失谐;(b)蓝失谐Fig.2.Atoms are trapped by dipole force:(a)Red-detuning case;(b)blue-detuning case.

通过改变激光束的偏振和它们的传播方向可以产生一维、二维和三维的光晶格.如图3所示,一维晶格简单的由一对正交的偏振行波组成,对于二维和三维的光晶格,已经发展了很多种不同的激光束配置.

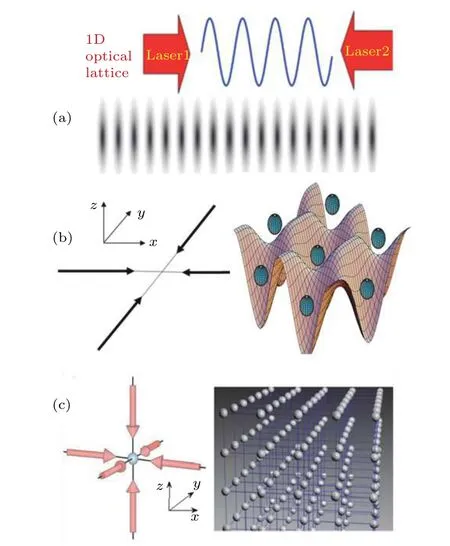
图3 一维、二维和三维光晶格的产生以及原子在晶格中分布的示意图 (a)一维光晶格;(b)二维光晶格;(c)三维光晶格[15,16]Fig.3.Optical lattice with different dimension and corresponding atomic distributions:(a)One-dimension case;(b)two-dimension case;(c)three-dimension case.

4 光晶格中的旋量凝聚体

4.1 势阱中的旋量凝聚体

这里仍然选择光势阱.和磁阱只能通过弱场搜寻囚禁单个超精细子能级的原子不同,光囚禁可以捕获所有磁子能级的原子.光势阱中自旋为旋量玻色-爱因斯坦凝聚体的哈密顿量的二次量子化形式为

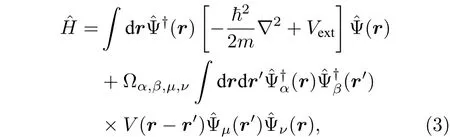
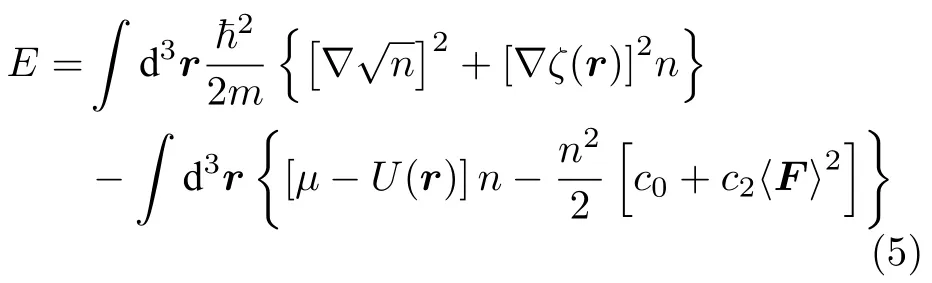
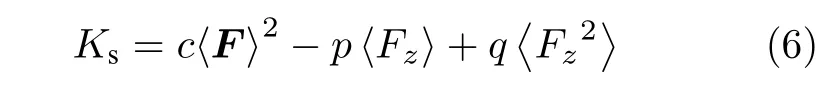
光晶格的光势阱列阵为我们研究多体相互作用提供了一个非常可靠的环境,将旋量凝聚体装载到光晶格中,在最低能带的瓦涅尔基中展开玻色场个格点的瓦涅尔函数,表示第个格点上-自旋组分的玻色湮灭算符.值得注意的是,自旋对称相互作用远远大于自旋非对称相互作用,即只有当时,不同自旋组分的原子才可以用同样的空间波函数描述.如果只考虑最近邻格点间的相互作用,哈密顿量(4）可以约化得到自旋的玻色-哈伯德模型[17]:

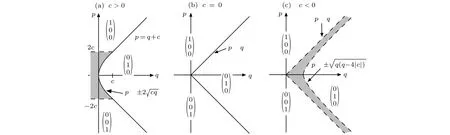
图4 旋量凝聚体的自旋畴示意图.图 (b) 中, 时凝聚原子会分成三个畴而且有明显的边界,相互作用会诱导畴边界交叠如图(a)和图(c)所示,在图(c)中自旋畴已经没有了明显边界[7]Fig.4.Spin-domain diagrams for condensates with .The cloud is separated into three domains with distinct boundaries in(b),components are miscible as shown in(a),all three components are generally miscible in(c).

5 光晶格中的自旋激发和磁孤子

5.1 光晶格中的自旋激发

光晶格中的旋量凝聚体的动力学行为主要是受到三种两体相互作用的影响:自旋交换碰撞相互作用、磁偶极-偶极相互作用、光诱导的偶极-偶极相互作用.对于蓝失谐的光晶格,原子被捕获的位置是波节处,这时光诱导的偶极-偶极相互作用可以忽略,很多工作都这样处理.

当势阱足够深的时候,体系会相变到莫特绝缘态.在没有外磁场作用的情况下,每个晶格中的凝聚原子可以看成是一个个独立的小磁子,并且它们的自旋指向是任意的,并没有格点间的自旋关联.此时,光晶格系统非常类似于磁学中的自旋格子系统,但是它们存在明显的差别.首先磁学中的交换相互作用在这里几乎可以忽略,毕竟小磁子之间约有半个波长的距离,莫特绝缘态的格子系统中格点间粒子交换也几乎是零.另外,由于玻色增强效应,在固体系统中经常被忽略的磁偶极-偶极相互作用这时开始发挥重要作用,如果格子中的平均粒子数,磁偶极相互作用可以获得平方量级的增强.

常用的磁偶极-偶极相互作用的形式为

由上两式可以看出,光晶格中旋量原子的哈密顿量和固体物理里的海森伯自旋链的哈密顿量形式非常相似,所以我们也称这个系统为光晶格中的原子自旋链模型.和海森伯自旋链相比,原子自旋链有两个独有的优点:其一是格点之间的耦合是长程耦合,充分考虑了非近邻格点间的相互作用;其二是耦合距离和强度可以调节,通过调节外场参数,可以增加或者减弱长程特性,特别地,适当调节参数可以实现近邻和次近邻的有效近似.由于磁偶极相互作用的存在,张卫平、蒲晗等[11]研究发现铁磁相变和自发磁化可以在一维自旋链中发生,如图5所示.

以上考虑都是没有光诱导的偶极-偶极相互作用的情况.在红失谐光晶格中,凝聚体被囚禁在驻波波腹,即光强最强处.这时需要考虑光诱导的偶极-偶极相互作用,其形式为[10]

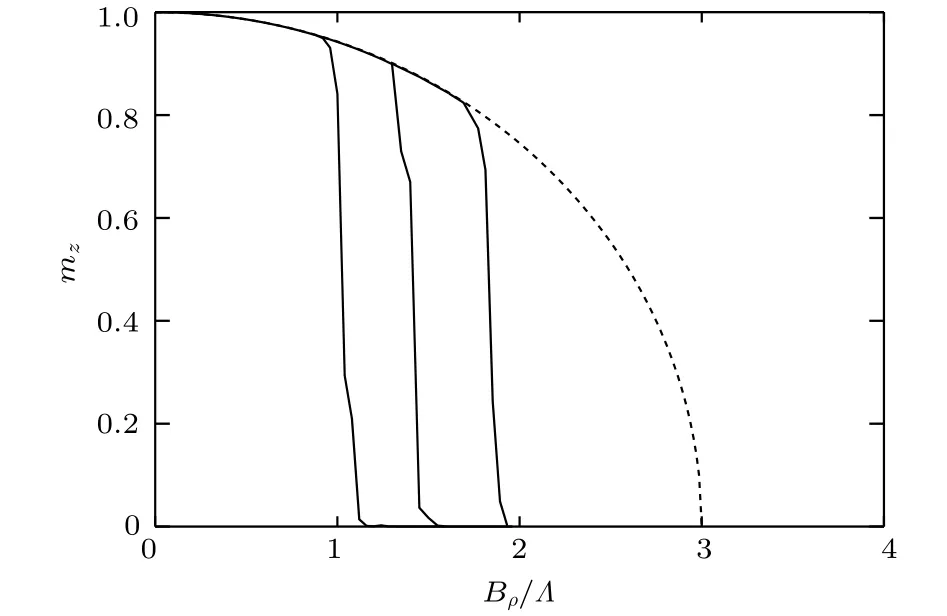
图5原子自旋链中磁偶极-偶极相互作用诱导的自发磁化[11]这里纵轴 代表 方向的自发磁化强度,横轴 是平面上的外磁场强度,虚线是平均场近似的结果,数值模拟所得实线对应的是不同的格点填充数Fig.5.Spontaneous magnetization of atomic spin chain dominated by magnetic dipole-dipole interaction. is the magnetization components in the -axis direction, is intensity of the external magnetic field.The dashed line represents the mean-field result and the solid lines,from left to right,correspond to the exact numerical results for a two-site lattice with atoms.

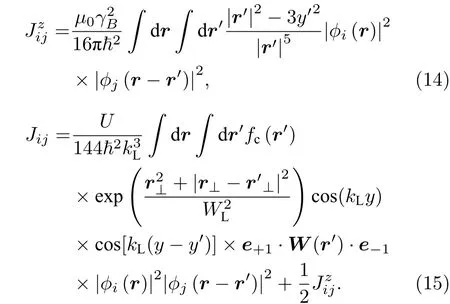
从方程(13）中可以看出,光诱导的偶极-偶极相互作用只是在平面起作用,而磁偶极-偶极相互作用在不同方向上都有贡献.方程(15）给出了光诱导的偶极-偶极相互作用在格点间耦合的分布,很明显的是这个耦合强度几乎完全依赖于外场的参数包括强度、频率和囚禁宽度.适当调节外场可以极大地增加格点之间的耦合强度,只要格点之间的耦合足够强,横向的自旋激发就会在格点上传播,这就导致晶格中原子的自旋扭曲在自旋链上传播.从哈密顿量(13）可以导出自旋激发的海森伯运动方程:

这个方程描述了自旋激发沿坐标轴方向的传输,非常类似于量子力学中有效质量为的粒子的质心运动方程.和声子定义类似,这就是光晶格原子自旋链系统中产生的磁振子.图6给出了原子自旋链中的自旋波产生和传播的示意图.

5.2 光晶格中的磁孤子

凝聚态物理发展过程中,孤子作为基态元激发的引入对处理非线性问题是巨大的推动,孤子激发在海森伯自旋链中已经被广泛研究过.在低温条件下,这些元激发实际就是我们上面提到的自旋波,自旋波孤子也是大家比较感兴趣的课题.只是在固体系统中,掺杂和缺陷一直存在,温度的影响也很大,增加了研究和观测的难度.这方面,光晶格系统的优越性很明显:一方面这里的原子自旋链系统是一个非常纯净的系统,没有任何杂质;另一方面,系统具有很高的可控性,而且温度的影响变得微乎其微.在这个意义上,光晶格可以作为一个非常理想的工具用来模拟固体物理中的许多动力学特征.

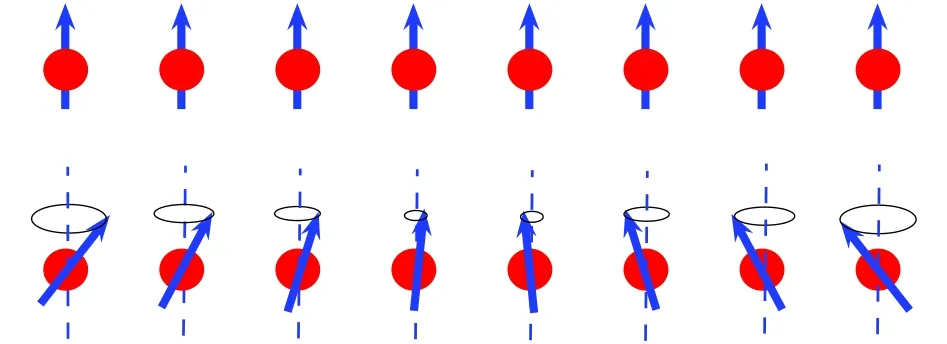
图6 原子自旋链中自旋波的激发.图的上部分是原子自旋链的铁磁基态示意图,下部分是偶极-偶极相互作用下自旋进动在晶格方向的传播[18]Fig.6.Spin waves are excited in atomic spin chain in optical lattice.Top:ferromagnetic ground-state structure of the spinor BEC atomic spin chain.Bottom:spin in each lattice site processes in spin space and spin waves can be excited.

基于偶极-偶极的可调性,原子自旋链中的磁孤子激发被大量地研究.但是,针对如何在原子自旋链中实现可观测的孤子的研究很有限.由于连续近似下自旋波的传播服从方程(17）,通过研究孤子存在的条件,我们建议通过调节横向场来实现磁孤子的观测.图7中给出了如何通过控制外部光场的强度和囚禁宽度来实现磁孤子激发.

6 光晶格中的磁激发应用于量子模拟

6.1 磁振子压缩态

近年来,随着精密测量的发展,压缩态无论从理论上还是实验上都得到极大的关注.在凝聚态物理中,有研究表明通过调节固体材料的参数可以实现磁振子的压缩态,这个方法实验上有很大的难度.如第1节所述,光晶格中的超冷原子系综由于其得天独厚的性质,为模拟传统凝聚体物理和固体物理中的复杂物理问题提供了一个理想环境.

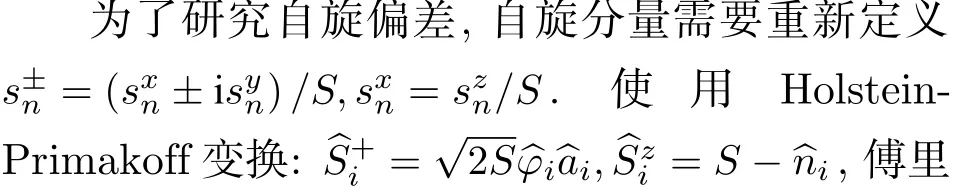
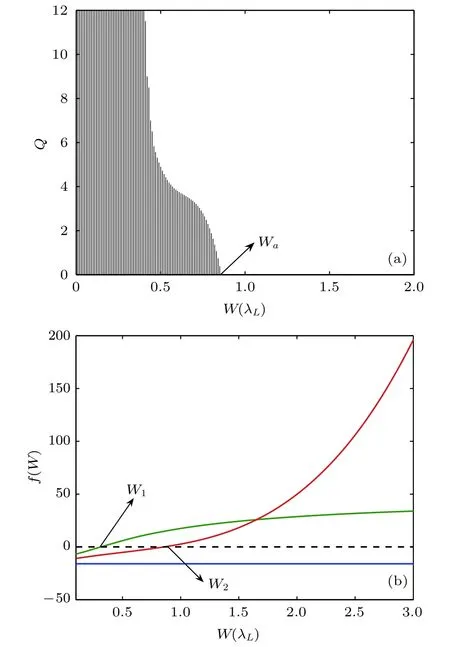
图7 通过控制外场实现磁孤子的产生(a)红失谐光晶格中控制驱动光场和束缚场产生磁孤子, Q 是驱动光场的强度, 是晶格的横向囚禁宽度,空白的区域对应有磁孤子产生,反之,暗的区域不能激发磁孤子;(b)蓝失谐光晶格中调节束缚场来产生磁孤子,蓝线、绿线和红线分别代表考虑近邻、次近邻和长程的结果, 代表有磁孤子激发[19]Fig.7.Magnetic soliton are excited by tuning external field:(a)Magnetic soliton are produced by tuning driving light field and trapping potential in red-detuning case, the vertical axis Q stands for the intensity of the modulated laser,and thehorizontal axis represents the transverse width of the condensate,the blank region corresponds to the existence of solitons;(b)magnetic soliton are produced by tuning trapping potential in blue-detuning case,the three lines correspond to the nearest-neighbor approximation (blue), the next-nearest-neighbor approximation(green),and the continuum limit approximation (red),respectively, magnetic solitons occur in the region.

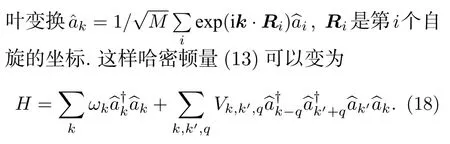
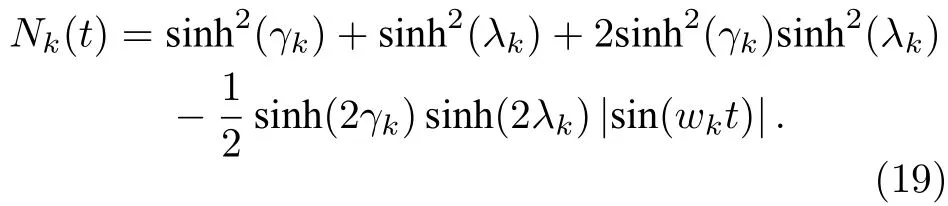
如图8给出了不同参数下磁振子的压缩特性.值得强调的是,这里磁振子的压缩态可以通过调节外部光场来实现,这种方式对系统的固有属性改变很小,在以往的系统中是很难实现的.

6.2 有限温度的动力学卡西米尔效应

对动力学卡西米尔效应这一有趣的物理学现象的实验观测也是近年来科学家们比较感兴趣的课题,很多设想的实验在实践过程中难度颇高.直到2011年,人们才在超导量子干涉设备中观测到比较完整的动力学卡西米尔效应[20].与此同时,实验过程中环境温度几乎是很难忽略的因素,这时有很多物理学家才开始研究有限温度的卡西米尔效应[21,22],这个方向的研究几乎都是理论层面的,所以急需找一个方便操控的系统实现实验观测.

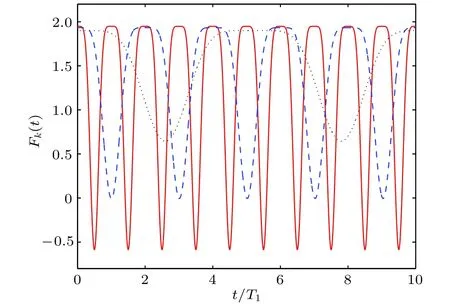
图8 通过调节束缚场实现磁振子压缩态实红线、绿虚线和黑实线分别对应于横向囚禁宽度为 的情况, 代表产生了压缩[19]Fig.8.Spin waves are excited in atomic spin chain in optical lattice.We choose three transverse trapping widths of the condensate: (solid red line),(dashed blue line), and (dotted black line),respectively, the magnon squeezing states occur when.

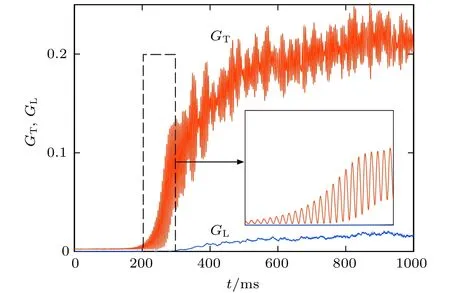
图9 外磁场驱动下囚禁势中旋量凝聚体的横向和纵向的磁化随时间的演化红线是横向的磁化 ,蓝线代表纵向的磁化 ,图中插图显示的是横向磁化被放大的过程[23]Fig.9.Time evolution of the average squared transverse magnetization (red curve) and longitudinal magnetization (blue curve),the exponential growth ofis shown in subgraph.

光晶格自旋链系统中,磁偶极-偶极相互作用和光诱导的偶极-偶极相互作用能诱导不同的自旋激发,这和理论上研究有限温度的动力学卡西米尔效应的光学共振腔系统非常相似.相对弱的磁偶极-偶极相互作用诱导的激发可以作为有限温度激发源,在外部光场的驱动下,我们发现磁振子激发会产生指数形式的增长,如图10所示.

7 结 论

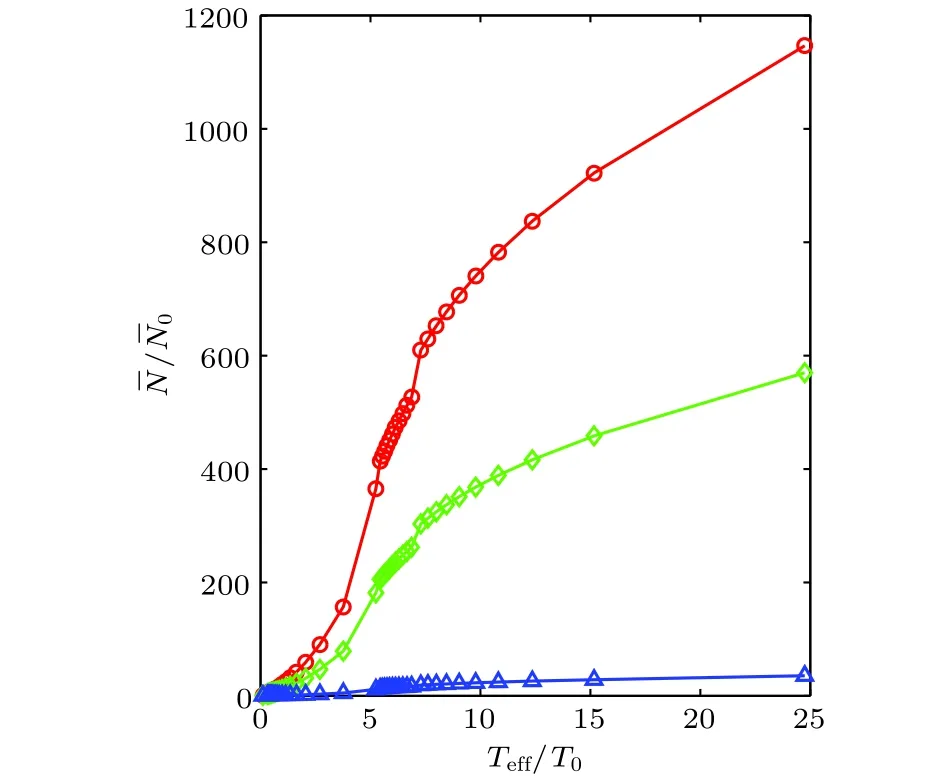
图10 不同强度的驱动场下自旋起伏的放大倍数随有效温度的变化图中红色圈、绿色方块和蓝色三角分别代表我们选择的不同的驱动光场强度,通过适当选择光场强度可以使磁振子激发产生指数形式的增长,也就是动力学卡西米尔效应[18]Fig.10.Amplification factor as a function of the effective temperature under different intensities of the external modulation laser,the the dynamical Casimir effect at finite temperature take place if the proper parameters are selected.

我们对光晶格原子自旋链的磁性的由来、操控和应用做了简要的理论回顾.光晶格中旋量BEC原子自旋链模型和固体物理中的自旋链模型有一定的相似性,同时差别也很显著.首先系统组成的元素不再是电子而是电中性的玻色原子,其基本相互作用不再是短程的交换相互作用,而是长程的偶极-偶极相互作用,其中磁偶极-偶极相互作用和光诱导的偶极-偶极相互作用的存在使得这个系统具有了更大的潜在应用价值.在这个理想模型中还存在额外的可控自由度,这就使得很多现象可以在理想的系统中进行观察.对晶格原子自旋和磁学性质的研究不仅是理论的拓展,未来可望在原子光学器件、集成原子光学及其原子芯片乃至量子计算与信息处理等的研究与应用中有广阔的应用前景.