光学微腔中一维费米气的磁性关联特性*

冯彦林 樊景涛 陈刚† 贾锁堂

1）(山西大学激光光谱研究所,量子光学与光量子器件国家重点实验室,太原 030006）

2）(山西大学极端光学协同创新中心,太原 030006）

对于准一维两组分费米气与光学微腔耦合的系统,证明了微腔光子的超辐射可以驱动原子系统的磁性转变,该磁性转变与原子的失谐以及费米子的填充数密切相关.对于无相互作用原子气,在超辐射相区内平均场近似合理.基于该近似,分析了不同的填充和失谐情况下体系的静态自旋结构因子,由此刻画出腔光子协助的磁性关联转变,并得到了依赖于微腔参数的相图.最后,对可行的实验参数做了相关讨论.

1 引 言

近年来,光学微腔中超冷原子气的量子特性受到了人们广泛的关注与探索[1−13].例如,实验上实现了玻色-爱因斯坦凝聚与光学微腔的耦合[3],该耦合诱导出原子间的有效长程相互作用,这种有效长程相互作用会与原子间的短程碰撞相互作用竞争,进而给出丰富的量子相[4−7].伴随着实验上的进展,越来越多的理论工作者也投身于该领域,并致力于新奇物理模型的构建.例如,理论上发展了包含微腔光子的广义玻色-哈伯德模型[8−10],预言了微腔诱导的自旋轨道耦合,并阐明了与该自旋轨道耦合相关的拓扑特性[11].最近,研究者又建立了周期振荡的腔光晶格模型,并发现该模型包含着丰富的Floquet动力学特性[12].

另一方面,原子间磁性关联的量子模拟一直以来都是物理学界的热点课题,近年来,该方向更是成果斐然.例如,基于光晶格冷原子系统,实验上观测到了短程的反铁磁关联[14−16]、隐藏的反铁磁关联[17]、不可约的自旋关联[18]以及反铁磁长程序[19]等.理论方面的研究包括,非相干超冷原子的密度关联效应[20]、三阱光学超晶格中自旋为1的超冷原子特性[21]以及周期驱动的费米-哈伯德模型中的磁性量子相变[22]等.我们注意到,目前关于冷原子磁性关联的研究大多集中于无动力学反馈的光晶格系统,而作为原子间相互作用的“中继站”,微腔光子在原子磁性构建过程中承担何种作用？对于这个问题,目前学术界还缺乏系统研究.最近,在超辐射相区外,研究者发现了红失谐于原子的微腔光子对原子磁序有重要影响[23].然而,在超辐射相区内,人们对腔光子-原子相互作用系统的具体磁性关联仍缺乏理解.因此,本文着重探索超辐射相区内原子的磁性关联问题.

本文的研究对象是一个准一维两组分的无相互作用费米气与光学微腔耦合的系统,分析了该系统中腔参数、原子的填充和原子的失谐对原子磁性关联的影响.具体地,对光场自由度取平均场近似,得到了腔场的超辐射相变,并计算了原子在方向的自旋结构因子.我们发现,微腔光子的超辐射对原子系统的磁性关联有重要影响,在合适参数条件下甚至会驱动磁性转变.当驱动光与原子蓝失谐时,调节腔参数,系统会由超辐射反铁磁关联度越到超辐射铁磁关联.红失谐的情况则与之完全不同,此时系统始终保持反铁磁关联.最后对可行的实验参数做了简单讨论.

2 模型和腔场的自洽平均场计算

我们考虑的系统是装载在准一维背景光晶格中的两组分费米气与高精度光学微腔的耦合.如图1(a)所示,准一维背景光晶格沿着腔轴排列,原子只沿腔轴方向运动,不仅与线偏振驱动的腔模耦合,且与沿方向入射的两束圆偏振的抽运光耦合.如图1(b)所示,我们考虑的原子包含四个内态,即两个简并的基态(和)与两个激发态(和).和(蓝色的实线)的跃迁由量子化的腔场引起且对应的单光子的拉比频率为,和(红色的虚线)的跃迁由两束横向的抽运光产生且对应的拉比频率为,抽运光和腔模形成两个拉曼过程使和耦合起来.为原子激发态的频率),且满足,量子化轴沿方向.

图1 (a)超冷费米气沿着腔轴 方向被俘获在准一维背景光学晶格中,费米气被两束圆偏振的横向(沿着 方向)抽运激光驱动,腔模由一束线偏振的纵向(沿着 方向)驱动光驱动;(b)费米子的能级跃迁图,图中相关的跃迁过程和符号的定义见正文Fig.1.(a)The ultracold fermions are trapped in a quasione-dimensional background optical lattice along the cavity axis . These fermions are pumped by two circularpolarized transverse(along )lasers and the cavity mode is driven by a linear-polarized longitudinal(along )laser.(b)the atomic energy levels and their transition.See main text for the corresponding transition processes and the definition of the labels.

在驱动光与原子的失谐为大失谐的条件下,我们绝热地去除掉原子的激发态,并作二次量子化,则系统可以用如下的哈密顿量描述:

当不考虑原子间相互作用时,光场原则上可以用平均场近似来刻画[2,11,23],即,且结合粒子数方程,得到如下自洽方程组:

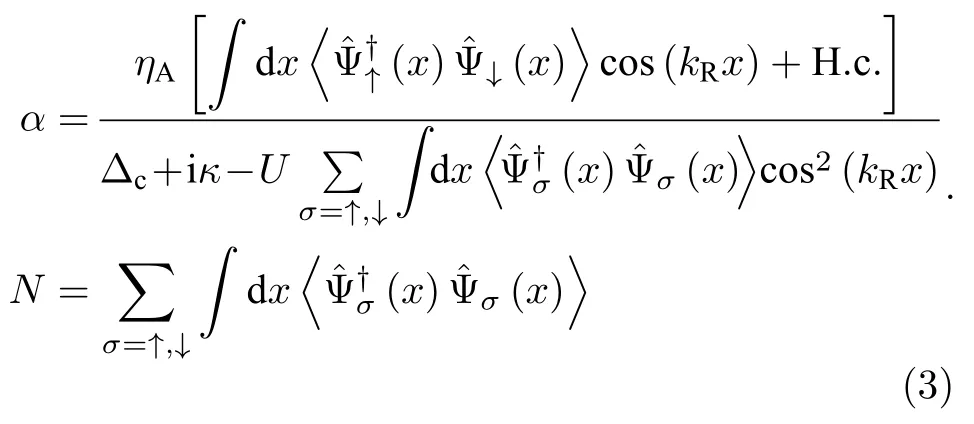
3 系统的磁性关联

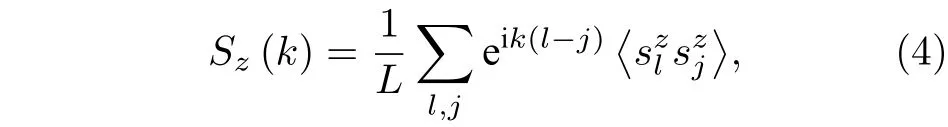
3.1 蓝失谐的情况

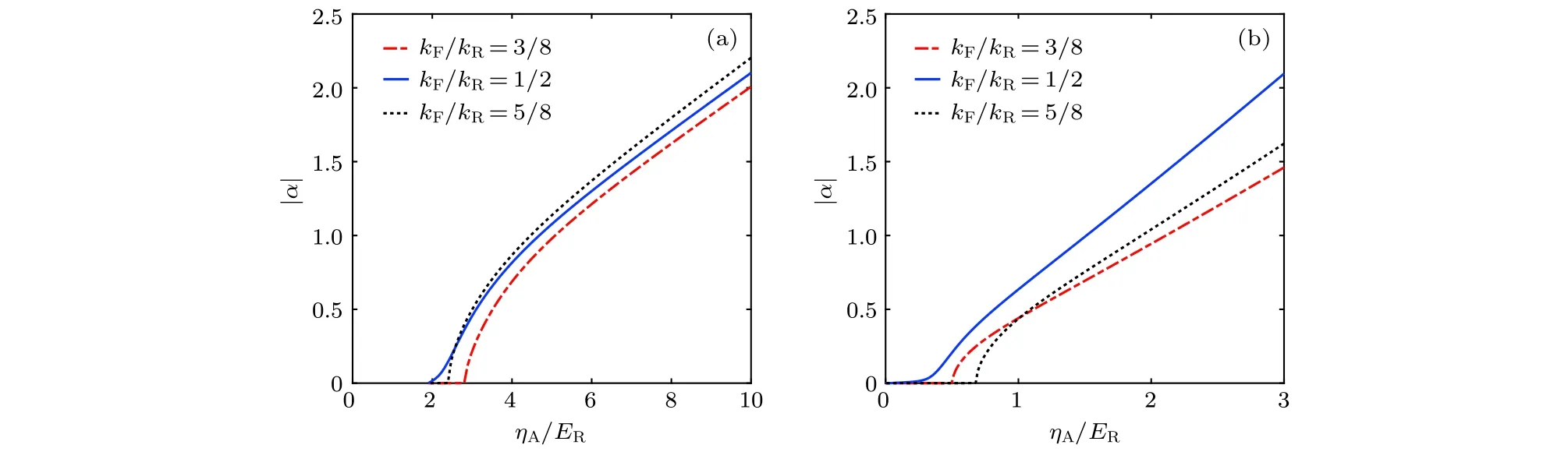
图2 a) 蓝 失 谐 的 情 况 ,光 场 在 不 同 的 晶 格 填 充 下 随 耦 合 强 度 的 变 化 .图 中 其 他 参 数 的 选 择 : , 在不同的晶格填充下随耦合强度的变化.图中其它参数的选择: , , , 和 .我们考虑的具有 80 个格点的晶格对应不同的填充,其中kF/ER不同的值对应不同的填充,kF为费米动量Fig.2.(a)The cavity field for systems in different fillings with .The plotted parameters are chosen as,The plotted parameters are chosen as , , , ,and .We consider a lattice of sites80with different fillings.

3.2 红失谐的情况

图3 静 态 自 旋 结 构 因 子 (a) ;(b) ;(c) .(图 中 对 应 的 其 它 参 数 的 选 择 与图2(a)中一致)Fig.3.The spin structure factors for systems in different fillings:(a) ;(b) ;(c)(The plotted parameters are the same as those in Fig.2(a)).

3.3 稳态相图

基于对上述磁性关联在两种不同失谐下的分析,我们现在可以得到在平面上的相图.我们可以通过在和处的峰值来判断不同的磁性,通过在处的峰值与其他处相等时给出磁性的相边界(图5）.图5(a)为蓝失谐情况下的相图,M表示金属相,AF-SR表示的是反铁磁关联的超辐射相,FM-SR表示的是铁磁关联的超辐射相,可以看出在不同填充情况下,调节系统可以实现从M相到AF-SR相和从AF-SR相到FM-SR相的越变.图5(b)为红失谐情况下的相图,可以看出在不同填充情况下,调节系统可以实现从M相到AF-SR相的越变.

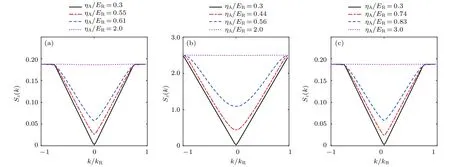
图4 静 态 自 旋 结 构 因 子 (a) ;(b) ;(c) (图 中 对 应 的 其 他 参 数 的 选 择 与图2(b)中一致)Fig.4.The spin structure factors for systems in different fillings:(a) ;(b) ;(c)(The plotted parameters are the same as those in Fig.2(b)).

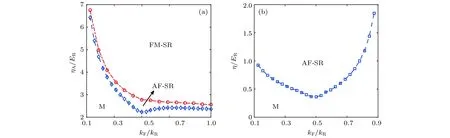
图5 (a)蓝失谐时 平面上的相图(M,AF-SR和FM-SR分别代表金属相、反铁磁关联的超辐射相和铁磁关联的超辐射相,其它参数的选择与图2(a)相同);(b)红失谐时 平面上的相图(AF-SR代表反铁磁关联的超辐射相,对应的其他参数的选择与图2(b)中一致)Fig.5.(a)The phase diagram in the plane for the system with blue-detuned atomic detuning(M,AF-SR,and FM-SR correspond to metallic phase,antiferromagnetic superradiant phase,and ferromagnetic superradiant phase,respectively.The plotted parameters are the same as those in Fig.2(a));(b)the phase diagram in the plane for the system with red-detuned atomic detuning (AF-SR corresponds to the antiferromagnetic superradiant phase.The plotted parameters are the same as those in Fig.2(b)).

4 参数估计

接下来我们简单讨论一下关于得到的不同的磁性关联相在实验上的探测.首先,超辐射反映在光子数的集体激发上.光子数实验可以使用校准的单光子计数模块对腔内光强进行实时监测[3].另外,关于磁性相变由自旋动力学结构因子体现,实验上可以通过探测透射光子来探测[33].因此,我们期望所预估的相图在实验中是可探测的.

5 总 结

在本文中,我们提出了一个实验上可行的方案并研究了由超辐射引起的准一维两组分费米气的磁性相变与原子的失谐以及费米子的填充数的关系.在不考虑原子间的相互作用时,我们利用平均场近似的方法得到了体系的超辐射相变,在此基础上,通过定性分析方向的自旋结构因子来研究系统的磁性转变.结果表明,有效的光与原子相互作用导致的自旋不守恒过程会使得系统发生磁性相变,且在蓝失谐时,通过调节腔参数,系统会实现由反铁磁关联的超辐射相到磁性关联超辐射的转变;相反地,在红失谐时,系统会得到反铁磁关联的超辐射相.在非半满填充的时候系统也具有类似的结果.