GPS桥梁监测系统的构建及其在某大桥中的应用研究

(中铁第四勘察设计院集团有限公司， 湖北 武汉 430063)

1 概述

近些年，随着我国建设技术的不断发展及交通量的急剧增加，我国建设特大桥梁数量越来越多[1]。众所周知，桥梁在各类荷载的作用下会发生变形和振动，这种现象在特大桥梁上尤为明显[2]。特大桥梁在风荷载的作用下会产生限幅、发散两种振动，其中限幅振动包括抖振和涡激振，发散振动包括驰振和颤振[3]。由于发散振动引起的桥梁事故屡见不鲜[4]，其危险性较大，需引起重视。对桥梁造型的不断个性化追求及桥梁跨度的不断增加，均会使得桥梁的振动加剧，增大桥梁的动力响应[5]。桥梁的工作状态及自身特性可通过阻尼系数、振型及自振频率等自振特征进行体现[6]。因此及时有效地对桥梁的自振特征进行监测可以评价桥梁的使用状态，及时发现桥梁结构的损伤，并根据监测结果制定相应的维修加固方案。目前，国内外对桥梁进行动态位移监测的仪器主要有加速度传感器、测量机器人及GPS等[7]。其中加速度传感器对桥梁的高频振动监测效果较为理想，但由于加速度传感器本身的技术原因，其无法对低频动力效应进行有效的监测，造成监测效果较差。此外，在进行位移计算时需要进行两次积分换算导致其位移的测量精度较低。测量机器人近几年发展较快，可以进行多点测量，在布设测点时也较为灵活。但是其与加速度传感器相似，对低频部分的测量精度较差，且受天气影响较大，无法在大雨、大雾等恶劣天气下进行测量。而GPS差分监测技术具有测量精度高、受天气影响小、监测成本低，且对高频及低频测量精度均可以满足要求，广泛应用于国内外的桥梁动态监测领域。广东虎门大桥、新加坡凌美大桥、香港明珠大桥等桥梁[8]均采用GPS差分监测技术进行长期监测。本文利用GPS差分监测技术构建了桥梁监测系统，并将其应用至江苏某大桥中。

2 GPS桥梁监测系统

GPS桥梁监测系统由控制中心、基准站、监测点及数据传输系统组成。在利用GPS进行桥梁的自振频率监测时，桥梁的自振频率与GPS仪器的采样频率需要满足Nyquist采样定理[9]。其表达式如式(1)所示。

(1)

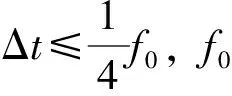
根据文献[10]，在利用GPS进行采样时，为保证采样的精准，一般选择待采样频率为实际采样频率的0.2～0.25。大型桥梁的自振频率一般低于2.7 Hz，在进行采样时，尽量使其频率高于10.5 Hz。在进行监测时，一般使用高精度的双频接收器进行频率的采集和接收[11]。

基准站的作用为接收卫星信号，将卫星信号通过数据传输系统传送给监测点。监测点的作用为接收观测卫星的信息和基准站发送的差分信息，其采集频率为10.5 Hz以上，并对采集到的信息进行相对差分处理，然后将处理后的信息传输至监控中心。监测点与基准站之间的距离会影响监测的精度，通过缩小两者之间的距离可以有效提高监测精度。监控中心的作用为接收各个监测点传输的监测数据，并通过数据整理软件进行数据处理，桥梁的振动状态以表、图等形式进行直观显示，从而得到桥梁的实时监测信息。经过系统授权的用户可以进行实时的查看。

综上可知，GPS监测系统的特点为自动化程度高，可实现实时监测；监测精度高，可同时对低频、高频的振动进行监测。

在利用GPS进行桥梁的实时动态监测时，求解双差整周模糊度[12]是整个过程的关键。目前一般采用OTF(On The Fly Ambiguity Resolution)法[13]进行求解，该方法又称整周模糊度动态解算法。其原理为通过协方差和流动站近似坐标的方式对整周模糊度的搜索空间进行确定，然后利用确定后的空间进行所有的模糊度解计算，基于得到的可能的模糊度利用比较最小方差选择次优解和最大优解，最终得到整周模糊度[14]。利用OTF法可以在5 s内确定所求的模糊度，其优点为在失锁后可以快速地再锁定卫星，避免了由于卫星发布的较大变化引起的长时间等待。OTF法的精度与PDOP值密切相关，PDOP值越大，结算精度越低，运算速度也就越慢[15]。将若干台接收机放置于基准站上，同时将若干台接收机放置于监测点上，流动站和基准站对相同的GPS装置发射的信号进行接收。

目前，载波动态相对定位基准站传送数据主要有2种方式：一种为移动站接收参照站发送的观测原始数据，然后在移动站上对数据进行双差处理并对移动站的三维坐标进行求解，此方法需要在移动站上进行计算，对数据链的要求较高。另一种方法为移动站接收参照站发送的测相伪距修正值，然后在移动站上对数据进行修正，最后得到流动站的准确位置，此方法不需要在移动站上进行计算，对数据链的要求较低。其过程相对简单，计算如下[16]：

基准站测相伪距：

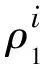
(2)

修正值：

(3)

将计算得到的修正值利用数据链传输至观测站，观测站对数据进行修正，然后利用修正后的数据通过计算得到观测点的坐标。本文建立的大桥GPS监测系统如图1所示。

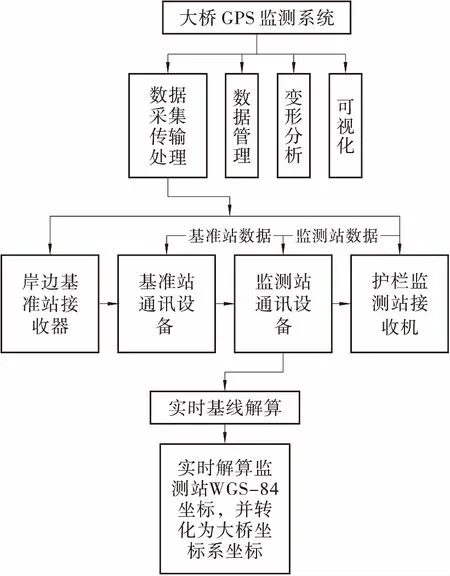
图1 GPS监控系统Figure 1 GPS monitoring system

一般情况下，对悬索桥和跨度较大的拉斜桥而言，在塔顶上布置塔柱摆动的监测点，每个塔柱布宜布设1个测点。桥面上的摆动、挠度及线形监测点一般布置在桥梁主梁的L/8、L/4和L/2处，其布设宜与锚固的受力点相互对应，并采用两侧对称布置的方案进行布置。以前数据传输一般采用光纤，其稳定性较好，但近几年随着通信技术的不断发展，4G通信技术可以有效对光纤进行替代。由于该系统应用的时间较长，需要建立数据库进行更新、备份和恢复等管理制度。

3 工程实例

某大桥是由斜拉桥和大型悬索桥组成的组合桥梁，其悬索桥的主跨为1200 m，为单跨双绞的支钢箱梁桥，该桥于2010年投入运营。图2为某大桥悬索桥部分的GPS接收机布置方案，在悬索桥主梁的L/4、L/2和3L/4的截面上布置了GPS接收机，每个截面上布置2套。采用密封盒放置GPS的天线并将其固定安装在箱梁外侧边缘处，信号接收机放置在外站的控制箱内。此外，为了对索塔进行变形监测，在2个索塔的塔顶各放置1个站点，相对应的基准站放置于大桥监控中心的楼顶处。

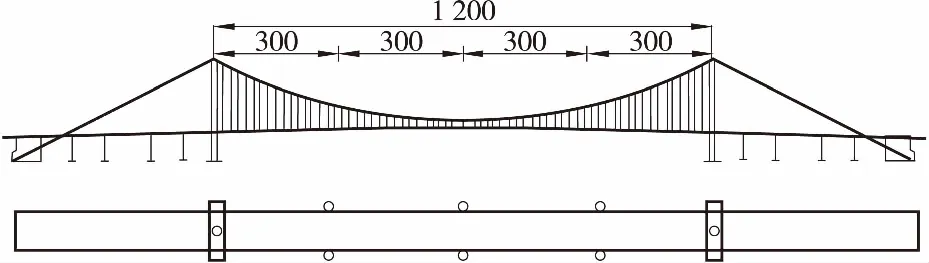
图2 某大桥测点布置图Figure 2 Location map of cangyang bridge

3.1 试验方案

本次试验共布置2台双频GPS接收机，一台作为基准点设置于北岸，编号G1；另一台布置于南岸的人行道栏杆内侧，编号G2，两台仪器之间的距离为934 m。两台GPS机器的周围环境均没有干扰源和遮挡，周围环境情况较利于观测。为了尽可能真实地反应桥梁的振动状态，利用测杆将GPS的天线与斜拉桥中部的栏杆固定在一起。

将GPS接收器的采样频率设置为12 Hz，将卫星高度角限值设置为14.5°。基于动态观测模式进行连续性观测，2测站同步观测时间为21.5 min。经调试后发现，12 Hz完全符合本次实验采样密度，观测当天天气较好，空中卫星可见8～9颗。

3.2 观测数据处理

本文在进行数据处理时，按照0.12 s的时间间隔对原始观测数据进行处理。进行数据处理时采用整周模糊度动态解算法。假设G1点为固定点，G2点为移动点，对其进行基线处理。根据计算结果可以得到G2在坐标系下东西方向、南北方向及垂直方向上的3个坐标，从而形成数据列。通过对2台GPS接收器的观测数据进行分析，0.1 s的间隔共得到14200个监测数据，图3～图5为G2监测点的时程曲线。根据图3～图5可得表1。

由表1可知，该结果未超出GPS测量的精度范围[17]，从而说明本次实验观测的质量较高，数据传输结果较为可靠，但如果需了解桥梁结构的自振特征，需对数据进行进一步的处理。

图3 数据处理结果(n方向)Figure 3 Data processing results (n direction)

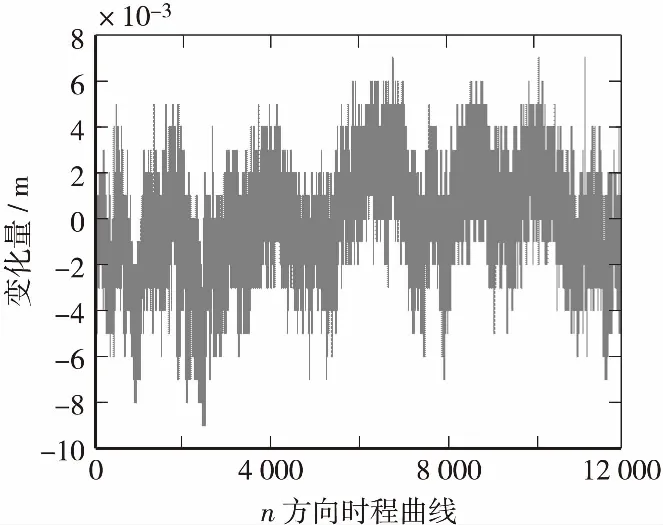
图4 数据处理结果(e方向)Figure 4 Data processing results (e direction)

图5 数据处理结果(h方向)Figure 5 Data processing results (h direction)

表1 各方向上的标准差及最大值Table 1 Standard deviation and maximum value of each partymm方向标准差最大值垂直向±11.2847.21南北向±2.6510.5东西向±2.257.05

3.3 频谱分析

频谱分析的原理[18]为按照信号源发出的信号按照频率依次展开，从而形成频率函数，分析并考察该频率函数的变化规律。本文采用傅立叶(Fourier)级数[19]转换进行分析。由于桥梁结构的质量非常大，相比对质量其结构的刚度相对较小，所以桥梁等大型结构的频率一般在0.15～12 Hz之间，频率较低。利用有限元仿真分析的方法对该大桥的主跨自振特征进行理论分析，可知其竖向的弯曲基振频率为0.248 5 Hz。根据前文可知，本文GPS观测数列的采用频率为10 Hz即0.1 s，其包括0.5～6 Hz，因此分析桥梁的固有频率是合适的。频谱分析可按公式(4)进行傅立叶变换(FFT)[20]处理，处理完后的频谱曲线如图6～图8所示。

(4)

图6 频谱图(n方向)Figure 6 Spectrum diagram (n direction)

图7 频谱图(e方向)Figure 7 Spectrum diagram (e direction)

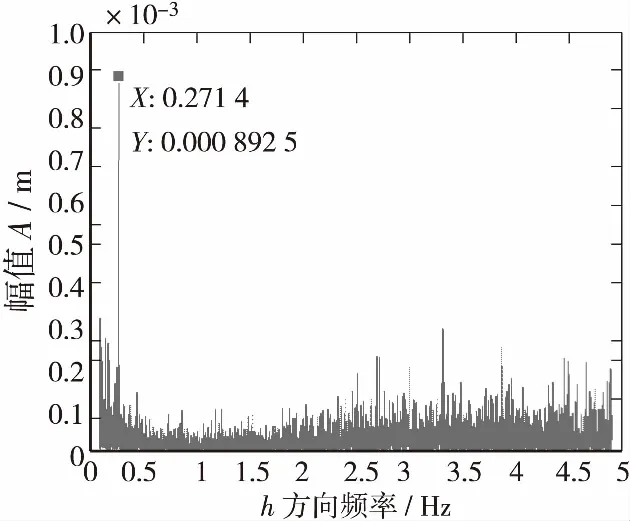
图8 频谱图(h方向)Figure 8 Spectrum diagram (h direction)

图6、图7、图8分别是G2在东西向、南北向、垂直向3个方向上的频谱图，其频率范围为0.10～0.49 Hz，去掉了0.49～5 Hz和0～0.10 Hz的数据。通过分析可知，东西向和南北向的幅值变化较小，而垂直向的幅值变化较大。这与有限元仿真分析得到的理论值结论不一致。其原因为存在一个奇点，经过数据处理后可知，其振幅为0.86 mm，频率为0.268 5 Hz。根据该桥梁的桥梁设计图纸中的计算书可知，桥梁在进行荷载试验时期弯曲基振频率值为0.269 8 Hz。与本次实验结果非常接近，误差仅为0.48%，而与有限元理论计算结果的0.248 5 Hz，误差也仅为8.04%。

4 结论

本文首先介绍了目前各种桥梁动态监测技术的优缺点，然后基于GPS测量技术构建了GPS桥梁监测系统，详细介绍了系统的组成、工作流程及数据处理方法。基于江苏某大桥，利用该系统进行了桥梁的动态监测，通过对测量数据的频谱分析及傅立叶变换(FFT)处理得到桥梁基振频率。将测量结果与有限元仿真理论计算结果及荷载试验得到的弯曲基振频率进行对比，三者结果非常接近，说明基于该系统的测量精度较高。