高速公路岩土边坡支护结构力学特征性分析

， ， ，

(1.云南国土资源职业学院，云南 昆明 652501； 2.昆明理工大学建筑工程学院，云南 昆明 650093)

21世纪以来，地球板块活动越来越活跃，地震发生的次数也越来越多，给人们的生命安全和财产带来了极大的威胁[1-2]。地震的发生会导致高速公路岩土边坡的支护结构失稳。因此，必须对地震作用下支护结构的最大震动力学参数进行深入的研究[3]。运用有限元分析软件构建高速公路岩土边坡支护结构力学有限元模型，输入地震波进行求解，并观察边坡支护结构的受力、变形情况，根据拟动力法模拟地震波的传播，充分考虑了纵波和横波从坡脚传播到坡顶的阻尼力对地震波的影响，获取地震作用下的力学响应规律[4]。

文献[5]提出一种基于圆弧滑动条分法的边坡支护结构稳定性分析方法，首先确定滑移面圆心坐标为几何控制参数, 根据各变量与滑移面圆心坐标之间的函数关系得到参数与内部稳定性安全系数之间的关系；利用网格法对框架预应力锚杆支护结构最危险滑移面的圆心坐标进行动态搜索和求解，再采用Matlab语言编制边坡支护结构的稳定性分析程序。文献[6]提出一种采用 Winkler弹性地基梁理论完成在地震作用下边坡支护结构的动力计算方法，考虑梁和挡土板的影响，推导出外框架—预应力锚杆—坡后土体三者协同工作的水平地震动力运动方程，获得解析解。

上述两种方法都没有考虑到高速公路岩土边坡支护结构稳定性各方面因素，导致计算获得的震动作用下的力学参数与实际参数不符。针对上述问题，提出一种高速公路岩土边坡支护结构力学有限元分析方法。

1 高速公路岩土边坡支护结构震动力学有限元分析

1.1 岩土边坡支护结构震动力学有限元模型

有限元分析方法是应用数学近似的方法模拟真实环境，有限元分析软件广泛的运用于工程项目中[7]。通过该软件可以模拟出边坡在外界环境作用下的最大震动的受力、稳定性等性能，通过有限元分析软件构建高速公路岩土边坡支护结构震动力学有限元模型。

首先对支护结构的坡面和结构面进行模型参数选取，如表1所示。

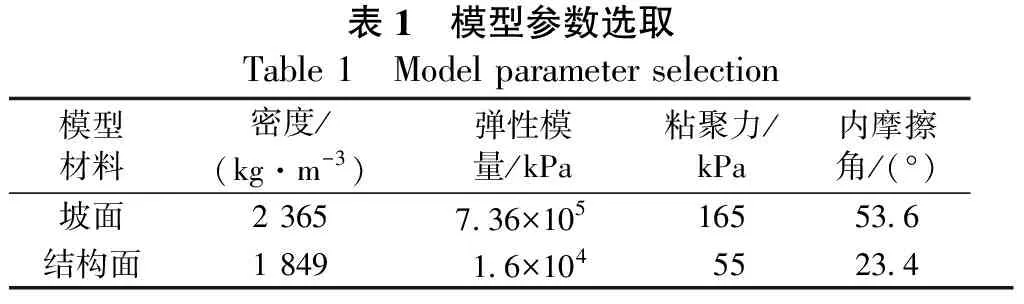
表1 模型参数选取Table 1 Model parameter selection模型材料密度/(kg·m-3)弹性模量/kPa粘聚力/kPa内摩擦角/(°)坡面2 3657.36×10516553.6结构面1 849 1.6×1045523.4

根据支护结构的坡面和结构面材料属性不同，利用有限元分析法建立模型的过程中，需要考虑到模型的切向力和压力两方面，由于各个材料之间互相不会影响，因此属于一种非线性问题[8]。

岩土边坡遭遇地震时，将地震波视为弹性波，在网格中的传播规律和在连续介质中的传播规律存在着一定的差异，利用有限元分析法建立的数学模型进行网格划分时，可能会出现一定的误差。原因在于当地震发生时，地震波作用与支护结构，支护结构上的质点根据最大的频率进行震动。则地震波震动频率大小与地震波速度和所划分的网格大小之间存在着一定的关系[9]，利用下式给出其表达式为：

ωc=2c/Δx

(1)

式中:ωc代表边坡支护结构第c震型的原始地震震动频率；c代表的是地震波速度；Δx为所划分网格的长度。

岩土边坡支护结构震动力学有限元模型划分网络的大小必须小于地震波最大震动频率所对应的地震波波长，因此选取震动最大频率为4 Hz的地震波，波长为50 m，网格划分尺寸为8 cm的要求，岩土边坡支护结构震动力学有限元模型网络划分如图1所示。

1.2 阻尼力的选取

支护结构在地震发生时会产生不规则的震动，则震动的过程中伴随着一定的阻尼影响，利用下式给出，阻尼矩阵表达式为：

[C]=α[M]+β[K]

(2)

式中:C、M、K分别代表地震发生时支护结构的阻尼矩阵、质量矩阵、刚度矩阵；α代表震动质量阻尼系数；β代表刚度阻尼系数；利用公式(3)和公式(4)分别给出α和β的求解为：

(3)

(4)

式中:ωj和ωi分别代表边坡支护结构第i震型和第j震型的原始地震震动频率；ξi和ξj分别代表边坡支护结构第i震型和第j震型的阻尼比；ξi和ξj的大小设定在1%～10%范围内。

1.3 高速公路岩土边坡支护结构震动力学参数测试

根据拟动力法模拟地震波的传播，充分考虑了纵波以及横波从坡脚传播到坡顶的相位差和阻尼力对地震波的影响，获取地震作用下的动力响应规律，计算岩土边坡在地震作用下的力学参数[10]。具体过程如下：

利用拟动力分析支护结构的稳定性，在分析过程中，采用正弦波替代地震波。水平、竖直方向的地震加速度随着高度、时间等变化的表达式为：

ah(z,t)=

(5)

ak(z,t)=

(6)

在上式中，ah(z,t)代表横向地震加速度；ak(z,t)代表纵向地震加速度；kh代表横向地震加速系数；kw代表纵向地震加速系数；w代表角速度；vs代表横向地震波的传输速度；vp代表纵向地震波的传输速度；H代表高度。

建立支护结构内的直角坐标系，设定顶点A在坐标系原点O。支护结构的坡面位于平面xOy内，其中，结构面ADB沿着y轴的方向运动，z轴的方向垂直向下，以下求解左、右线的余弦表示为：

(7)

(8)

α=θ1+θ2

(9)

l0=-cotδ2/e0

(10)

m0=-cotδ2cotθ2/e0

(11)

a.ACB面，根据三角形的性质，得到BC、A′C′的长度和ΔACB的面积表示为：

(12)

(13)

(14)

上式中，t=ze0。

b.ADB面。根据三角形的几何性质获取BD、A′D′的长度以及ΔADB的面积表示为：

(15)

(16)

(17)

c.CDB面。根据三角形的几何性质，得到CD、C′D′的长度以及ΔA′C′D′的面积表示为：

(18)

(19)

(20)

以下给出微元体A′C′D′的体积dv可以表示为：

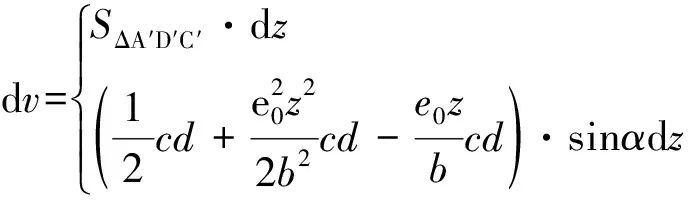
(21)

以下给出微元体A′C′D′的质量dm可以表示为：

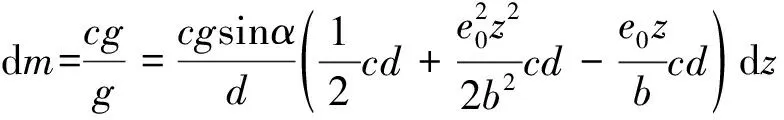
(22)

如果设定支护结构上的重力为W，利用下式给出ABCD的重力表达式为：

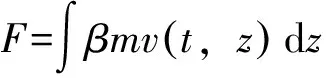
(23)

式中:β代表阻尼常数；m代表支护结构体质量；v(t,z)代表地震波的传输速度。一般可以通过地震波的加速度对时间的积分计算获取，计算式为：

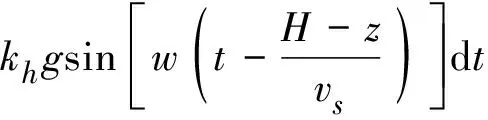
(24)

综上所述，地震波在岩土边坡支护结构中沿水平方向的传播速度可以表示为：

(25)

通过几何关系，获取棱线AB的视角表示为：

tanδ′=tanδ1sinθ1

(26)

根据几何关系计算不同垂直棱线的视倾角为：

(27)

通过上述计算，可知力学参数表达式为：

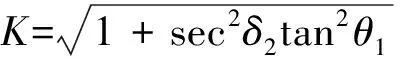
(28)

2 结果分析

为了验证所提出方法的综合有效性，需要进行测试，实验相关参数取值：高速公路岩土边坡支护结构弹性模量为E≈0.255 MPa，粘聚力为c1=c2=0.05 MPa，内摩擦角为φ1=φ2≈23.3°，高速公路岩土边坡支护结构密度为ρ=2 300～2 600 kg/m3，阻尼参数为α=0.6，地震波参数取值为：横向地震加速度参数取值为kh=0～0.5，纵向地震加速度参数取值kv为kh=0～0.5的一半，最大震动参数f=1～2，地震波周期为T=0.3 s，滑坡参数最小值为1.692。

分别研究支护结构内摩擦角、结构面粘聚力、横向地震加速度参数和最大震动系数对力学参数的影响，参数取值为：最大震动系数为f=1.4，横向地震加速度参数为kh=0.3，地震时间为t=0.2 s，测试结果如图2～图5所示。

图2为支护结构结构面内摩擦角对力学参数的影响。分析图2可知,当岩土边坡支护结构力学参数随着结构面内摩擦角的增加而随之增加。测试结果表明，当结构面内摩擦角不断的增加，岩土边坡支护结构力学参数相对稳定。

图3为支护结构结构面粘聚力对力学参数的影响。分析图3可知,当力学参数随着边坡结构面粘聚力的增加而随之增加。测试结果表明，结构面粘聚力增强了力学参数的稳定性。

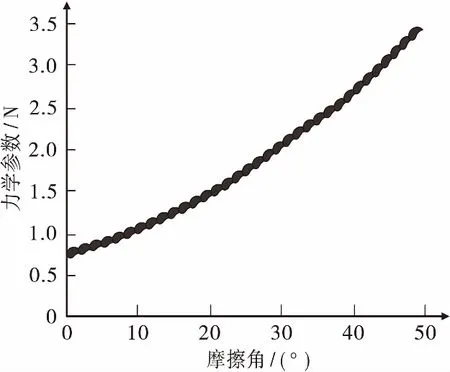
图2 支护结构结构面内摩擦角对力学参数影响Figure 2 Effect of in-plane friction angle of support structure on mechanical parameters

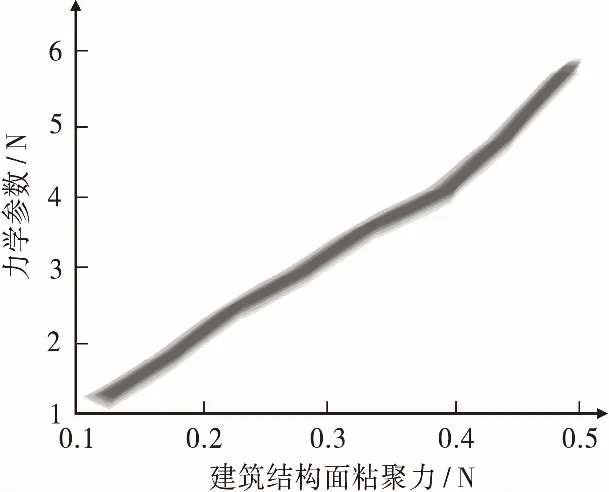
图3 支护结构结构面粘聚力对力学参数影响Figure 3 Effect of cohesion on the mechanical parameters of the supporting structure

图4 横向地震加速度系数对力学参数影响Figure 4 Effect of lateral seismic acceleration coefficient on mechanical parameters

图5 地震最大震动系数对力学参数影响Figure 5 Influence of seismic maximum vibration coefficient on mechanical parameters

图4为地震横向加速度系数对力学参数的影响。分析图4可知,岩土边坡支护结构力学参数随着加速度的不断增加而较小。测试结果表明，当地震横向加速度增大时，则会对滑坡参数造成一定的破坏。

图5为地震最大震动系数对滑坡参数的影响。分析图5可知，支护结构力学参数随着地震最大震动系数的增加而逐渐减小。测试结果表明，当最大震动增大时，则会对力学参数造成一定破坏。

3 结论

提出高速公路边坡支护结构的震动力学有限元分析方法。运用有限元分析软件构建支护结构力学有限元模型，输入地震波进行求解，并观察高速公路边坡支护结构的受力、变形情况，根据拟动力法模拟地震波的传播，充分考虑了纵波和横波从坡脚传播到坡顶的阻尼力对地震波的影响，获取地震作用下的动力响应规律，求出支护结构在地震作用下的力学参数。运用该方法得到支护结构结构面内摩擦角、粘聚力、横向地震加速度、最大震动系数等力学参数的影响分析。分析结果表明：

a.当结构面内摩擦角不断的增加，支护结构结构面的力学参数相对稳定。

b.结构面粘聚力增强了力学参数的稳定性。

c.当地震横向加速度增大时，则会对力学参数造成一定的破坏。

d.当最大震动增大时，则会对滑坡参数造成一定破坏。