新型深水绷紧式系泊系统动力特性分析

2019-03-14朱忠显神和龙

船舶力学 2019年2期

朱忠显，尹勇，神和龙

（大连海事大学航海动态仿真和控制实验室，辽宁大连116026）

0 引言

随着科学技术的发展和人类对油气资源的需求不断增加，海洋油气资源的开发逐渐向深海延伸，海洋浮式结构物的定位技术面临巨大的挑战。传统的悬链式系泊系统采用刚链或刚缆作为主体系缆，依靠系缆自重实现对其上部浮体的定位。但随着工作水深的增加，浮式结构物需要更长的锚链系泊，从而导致更大的系泊半径、较低的回复效率、更大的缆索自重和较小的平台有效承载能力等缺陷，限制了其在深水和超深水中的应用[1]。新型绷紧式系泊系统使用合成纤维缆作为主体系缆，依靠系缆张力提供高效的回复力。这种系缆因自重更轻、系泊半径更小、成本更低，且具有较高的断裂强度，在深水和超深水应用中具有明显的优势而倍受关注，现已被广泛应用于深水平台的系泊系统中。

合成纤维缆具有复杂的材料非线性特性，即粘弹性和粘塑性，使得准确把握系缆在复杂海洋环境条件下的动力响应非常困难。随着合成纤维在海洋工程系泊系统中的应用越来越广泛，对纤维缆材料的研究也越来越受到重视，人们开始尝试将系缆的材料特性应用到系泊线动力分析中去。目前，无论在理论、实验和数值分析方面，针对这种新型深水系泊系统的研究都处于起步阶段。

1 合成纤维系缆的动刚度特性及求解方法

1.1 合成纤维缆动刚度特性的研究

Del Vacchio[2]对聚酯纤维缆进行了模型实验，指出平均张力、张力幅值和载荷周期是影响弹性模量的主要因素，并给出了常温、循环载荷作用下纤维系缆的弹性模量经验公式。1999年，Bosman和Hooker[3]以Del Vacchio的经验公式为基础，通过实验研究发现平均载荷是影响动刚度的主要因素。Casey等[4-5]对聚酯纤维缆进行了大量的模型实验，给出了多组经验公式参数。2004年，Kim[6]采用迭代法对聚酯纤维缆的动刚度进行求解，并将动刚度特性引入到系缆的动力响应分析中。2008年Tahar和Kim[7]在柔性杆理论和有限元法的基础上，引入系缆的动刚度特性对聚酯纤维系缆进行了分析。2008年，Francois和Davies[8]通过模型试验指出在随机载荷作用下，平均张力是影响动刚度值的最主要因素。2006年，刘海笑和黄泽伟[9-10]在对绷紧式系泊系统的数值分析中考虑了纤维系缆的动刚度特性，并以一座工作于1 500 m水深的Spar平台为例进行了计算。2014年张火明等[11]对循环载荷下纤维系缆的动刚度特性进行了研究，改进了系缆动刚度和动张力的计算方法，编制C++程序求解系缆的动刚度，并以一座工作于1 500 m水深的Spar平台为例进行了计算，将计算结果与文献[9]进行对比与验证。

1.2 合成纤维系缆的动刚度特性

由合成纤维系缆构成的系泊系统，其响应和性能主要取决于系缆的轴向刚度（E×A）特性（其中E为系缆的弹性模量，A为横截面积），轴向刚度的准确表达是精确计算平台运动及系缆张力响应的基础。简化计算中通常引入一个经验公式来描述合成纤维缆在循环载荷作用下的动刚度特性。

其中：Lm为平均张力占最小破断强度（MBL）的百分比；La为动态张力幅值占最小破断强度的百分比；系数α、β和γ是与合成纤维缆构造相关的参数。

1.3 动刚度求解

纤维系缆动刚度的求解分两步进行：

（1）求平均张力。用静刚度模型k0=（E× A ）0/MBL（k0是由制造商提供的定值，一般在较低的单向载荷下测得，与缆绳自身特性相关）计算平均张力，得到Lm。若浮体在平衡位置左右做简谐振动，系缆的预张力即为平均张力。

（2）迭代计算动刚度。由静刚度模型可以计算出系缆平均张力，也可求得张力变化幅值La，但该La与真实动刚度情况下的La相差较大，须通过迭代的方法求解，将Lm和La代入公式（1）中，计算得到一个新的动刚度值k1。利用k1计算得到的新的系缆张力及La，再将La代入公式（1），求解动刚度值k2…如此反复迭代，直到相邻两次的动刚度计算结果ki-ki-1小于设定的容差值，认为计算收敛，ki即为所求得的动刚度值。

2 系泊线动力学模型

在深水工作环境下，系泊线的动力响应要比静力响应严重得多，结构物系泊系统动力响应计算成为海洋工程结构设计中的一个关键问题。

系泊系统动力学建模方法有集中质量法、有限元法和有限差分法等。其中，集中质量法因物理意义明确，算法简单易懂，具有广泛的适用性及扩展性而得到广泛应用。该方法由Walton和Polchaton[12]最先提出，Thomas[13]对模型进行了改进，Chai等[14]将集中质量法进行了扩展，并将弯矩、扭矩、与海底的接触问题等加入到海洋缆索的计算模型中。王飞等[15-18]基于集中质量法建立了拖缆动力学模型，同时考虑了弯矩、拖缆-海底接触等的响应，实现了拖缆的收放过程模拟。

2.1 坐标系定义

系泊系统的动力学模型应该建立在合适的坐标系下，根据需要建立如图1所示的惯性坐标系o-xyz和局部坐标系i-btn。惯性坐标系是空间固定的坐标系，所有的计算均转换到该坐标系下进行，其原点位于系泊系统末端与锚的连接处，长度记为s=0。局部坐标系附在系泊线上，t轴为微元的切线方向，指向长度s增加方向，n和b分别为法向和副法向；欧拉角（φ,θ）为微元段的姿态角。两个坐标系均为右手系，通过姿态角（φ,θ）进行关联。局部坐标系到惯性坐标系的转换矩阵为：

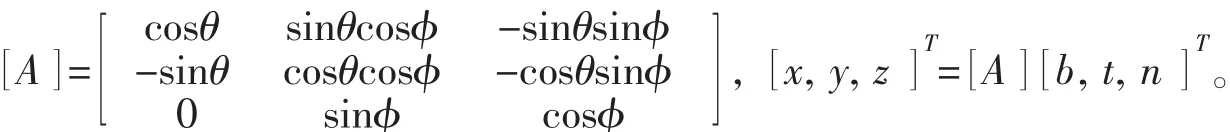
矩阵[A]为单位正交矩阵，其逆矩阵为其转置矩阵。

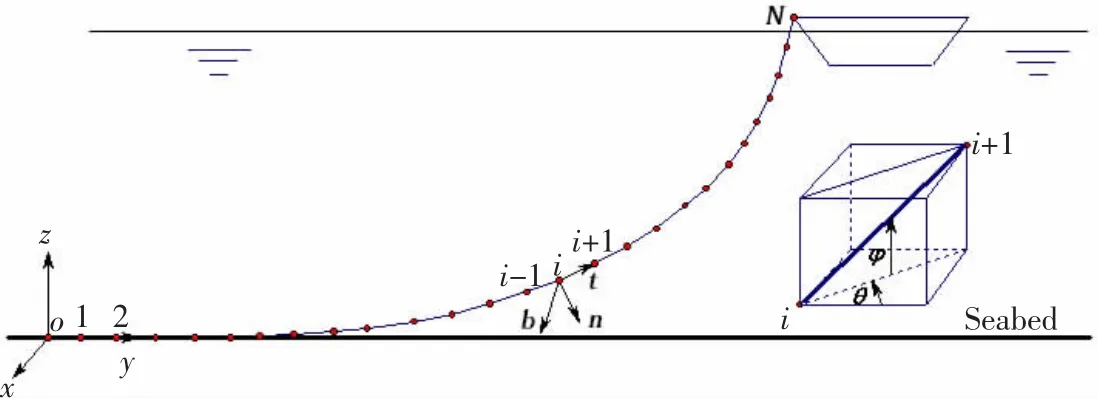
图1 系泊系统坐标系Fig.1 Coordinate system of the mooring system

2.2 系泊系统动力学模型

本文基于集中质量法建立系泊系统的动力学模型，将系泊线在空间上离散为一系列节点。系泊线总长度为S，末端s=0为第i=0个节点，上端点处s=S，为第i=N个节点。任取一微元段ds进行受力分析并应用牛顿第二定律，得到第i个节点的控制方程：

（1）质量矩阵

包括微元段惯性质量mi和其在水中的附加质量Mai，均取节点两侧微元段质量和附加质量的一半之和：

（2）浮力和重力

（3）流体阻力

按Ablow[19]和Huang[20]等人的方法：

在局部坐标系下的流体阻力为：

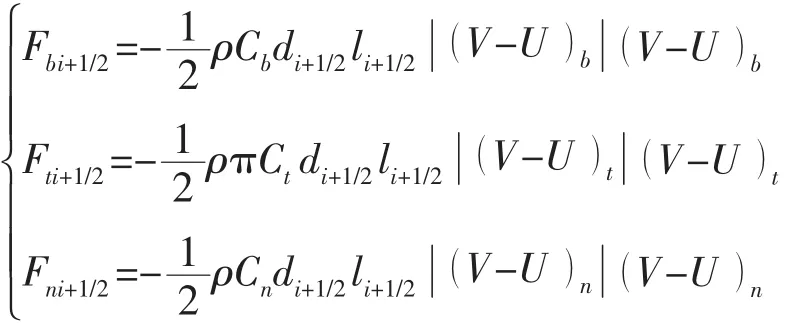
（4）张力

由系缆的材料特性和形变确定。合成纤维系缆的应力-应变关系不是简单的线性关系，它受系缆的构造形式、材料、载荷类型等影响。为将纤维缆的材料特性引入到系泊线的动力分析中，采用误差控制的迭代方法求解微元的动刚度和动张力：

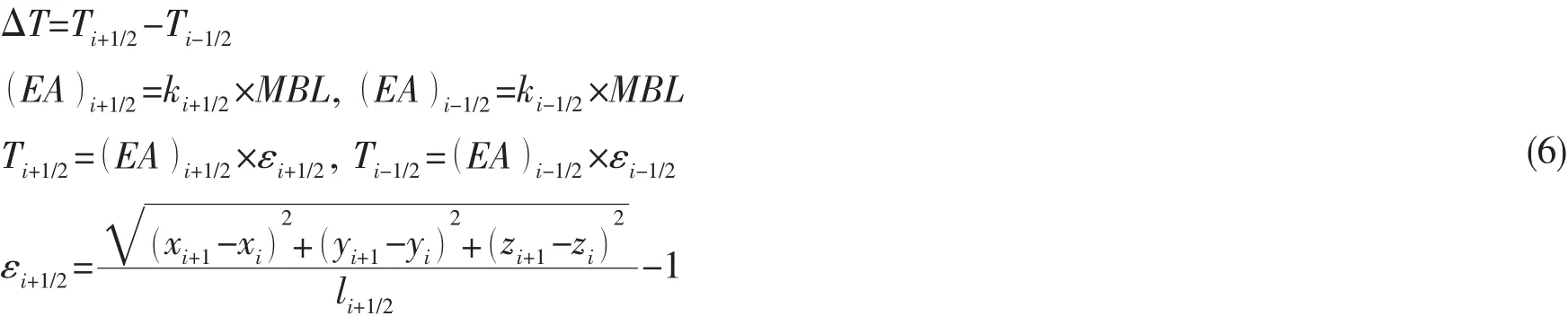
2.3 动力学模型数值求解

（1）边界条件。锚端边界条件设置为固定端；另一边界条件为系泊线顶端，其位置和速度与平台的运动保持一致：

其中：xs、ys、zs、us、vs、ws分别为系泊线顶端的位置和速度，它们是时间的函数。

（2）初始条件。用来确定初始时刻所有节点的位置和速度：

其中：等式右侧部分为给定的初始值，一般系锚泊系统两端位置固定状态为稳定状态。

（3）数值求解。联立控制方程（2），再加上给定的初始条件，并由，得到完整的偏微分方程组：

对方程组采用四阶显式龙格-库塔法进行积分求解，由各节点在tn时刻运动状态即可得到tn+1=tn+Δt时刻的运动状态。

3 传统动刚度数值求解方法

以一座工作于1 500 m水深的Spar平台为例进行计算，该平台采用绷紧式系泊系统，结构如图2所示，它由3组均匀布置的聚酯纤维缆组成，各组之间的间隔为120°。每组3根系缆之间间隔为5°。系缆参数取自文献[9，11]，如表1所示。为方便计算，选取5号系缆作为研究对象。如图3所示，假设平台沿x方向运动，系缆上端随平台主体发生位移，位移随着时间的变化历程为正弦函数：x（t）=x0sin（2πt/T ）。x0取 5.0 m，T 取 10 s。

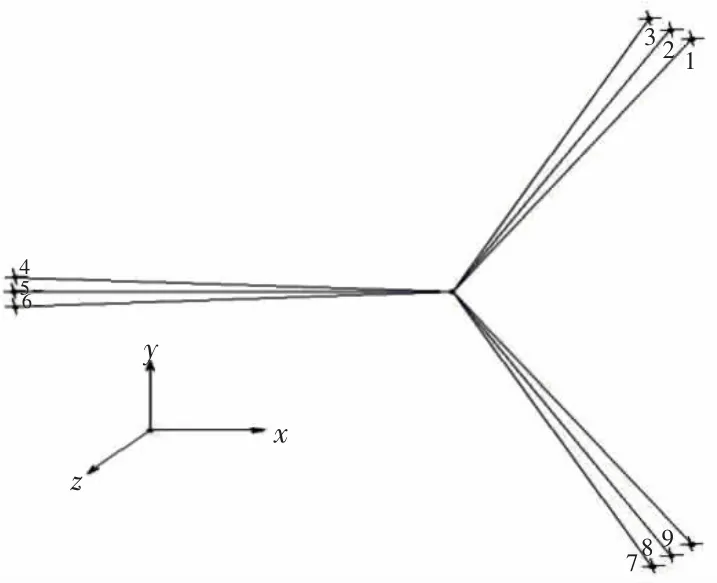
图2 系泊系统平面布置图Fig.2 General arrangement of the mooring system

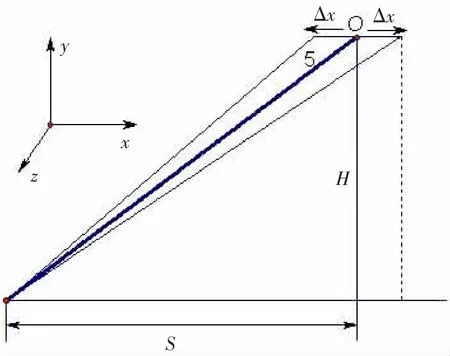
图3 系缆上端点运动示意图Fig.3 Sketch of the upper node's movement

传统动刚度计算[9-11]中将整根系缆作为一条直线考虑，假定系缆上应力和应变处处相同，认为合成纤维系缆的密度与海水密度十分接近，因而不考虑系缆的自重，且系缆所受的流体阻力相对于轴向张力较小，亦忽略不计。因假设上部浮体在平衡位置左右做简谐振动，系缆的预张力即为平均张力。

由表1提供的参数可得系缆静态轴向刚度：（EA ）0=k0×MBL=12.2×14 700×103=1.794 3×105kN，将该静刚度值用于动力学模型中张力的计算，并将计算结果与采用动刚度方法的计算结果进行比较。图4为采用静刚度和动刚度方法计算得到的系泊线张力，结果表明动刚度下系泊线最大张力比静刚度下大28.5%，最小张力比静刚度下大39.5%。图5为迭代计算得到的动刚度值，它随着上部浮体的运动而呈周期变化。显然，在合成纤维缆动张力计算中使用静刚度将无法精确得到缆索上的轴向张力，必须考虑合成纤维缆的动刚度特性。

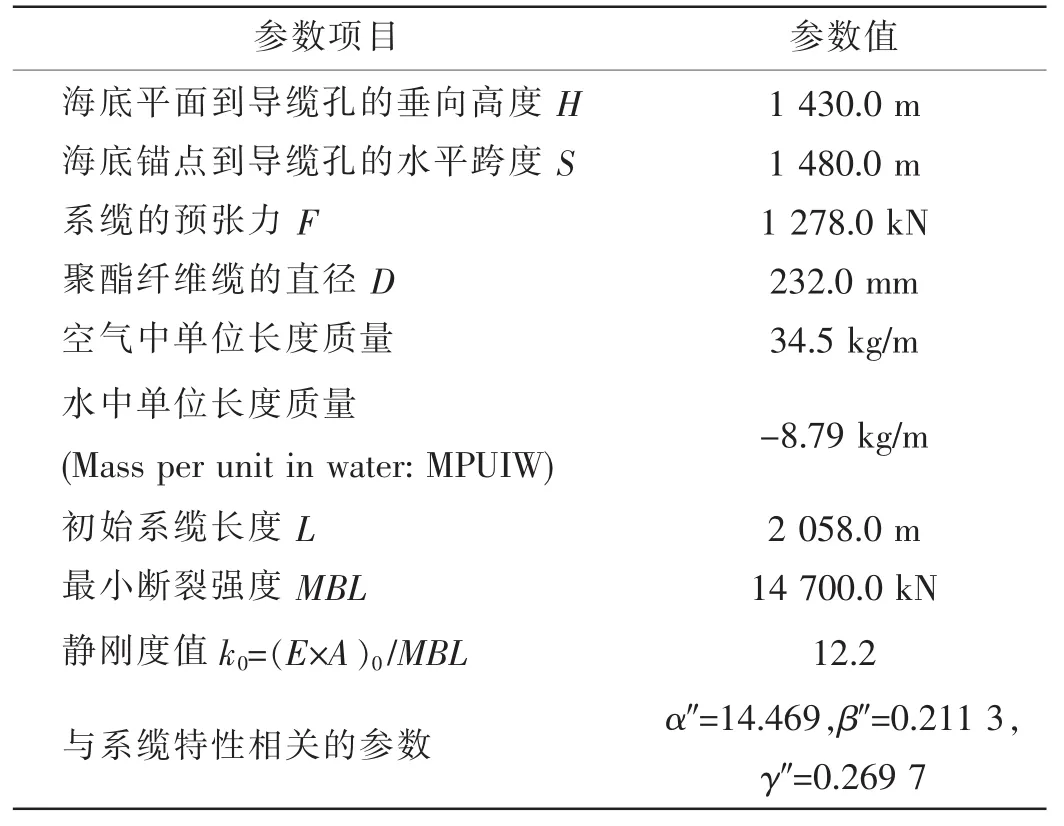
表1 系缆参数Tab.1 Properties of the mooring line

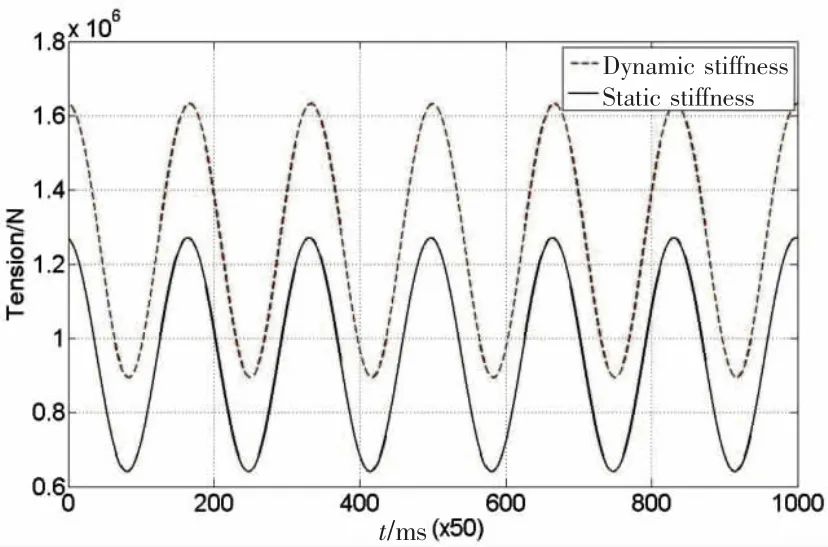
图4 张力时间历程Fig.4 Variation with time of the tensions

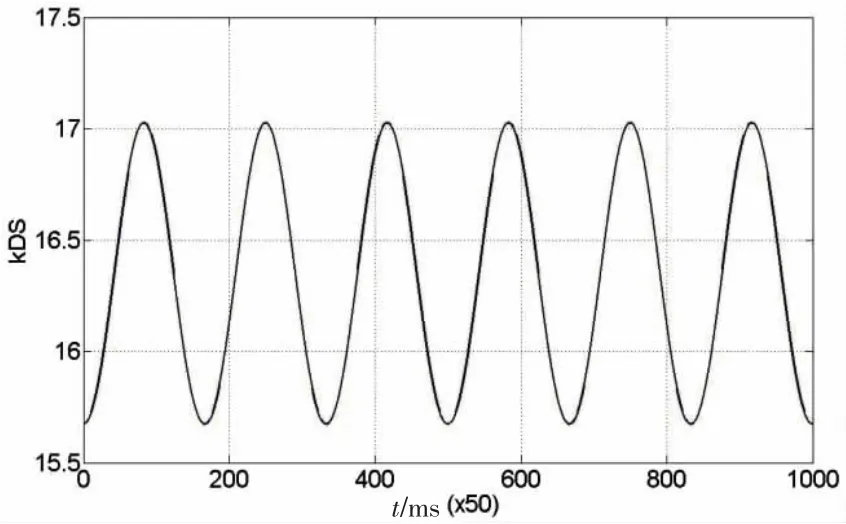
图5 动刚度值时间历程Fig.5 Variation with time of the dynamic stiffness

4 分段动刚度计算

传统动刚度求解方法虽然大大简化了计算，但也损失了计算精度。首先，系缆在水中的总浮重为8.79×2 058.0×9.81=177.46 kN，达平均张力（1 278.0 kN）的13.89%，忽略这部分的影响显然是不合适的；其次，系缆在激励下的形状并不是一条直线，如图6所示系缆上的张力同一时刻也并非处处相等，下部点的响应比其上部点要滞后；最后，传统方法无法考察流体动力对动张力的影响。为了精确计算绷紧式系泊线上的动张力，本文将合成纤维缆的动刚度特性引入到系泊线的动力学分析中，对每一缆段采用迭代的方法分别计算其动刚度和动张力。

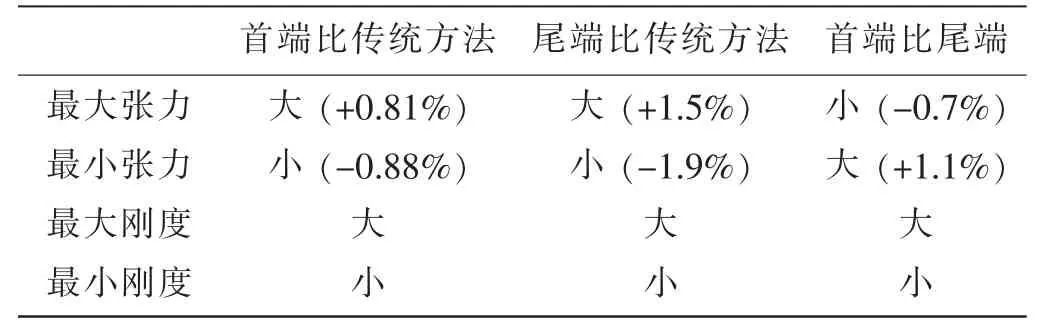
表2 分段动刚度下计算结果Tab.2 Results using sectional dynamic stiffness

图6为采用分段动刚度计算得到的首尾两端动张力的时间历程，图7为首尾两端动刚度值的时间历程，表2为计算结果与传统方法的比较，可以看出采用分段动刚度计算得到的最大张力比传统方法略大，首端比尾端稍小，最小张力则比传统方法略小，首端比尾端稍大；最大动刚度值比传统方法大，首端比尾端稍大，最小动刚度值则比传统方法略小，首端比尾端稍小。这是在动力学模型中引入了流体动力的结果。

图6 张力时间历程Fig.6 Variation with time of the tension

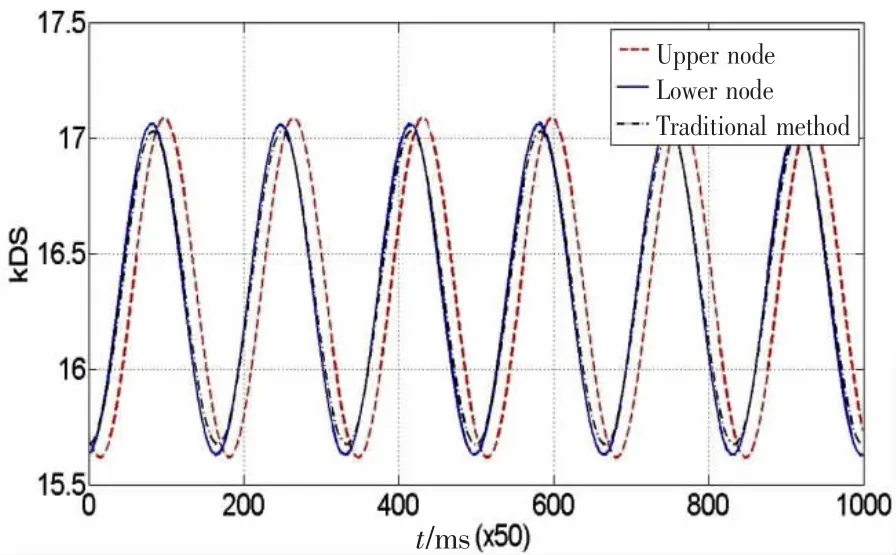
图7 动刚度值时间历程Fig.7 Variation with time of the dynamic stiffness

5 系缆自身重量的影响

传统方法计算动刚度时为计算简便忽略了系缆自身重量的影响。然而系缆长度较大，自身重量产生的总体作用不可忽略。本节在考虑系缆自身重量的情况下计算各缆段上的动刚度值和动张力。

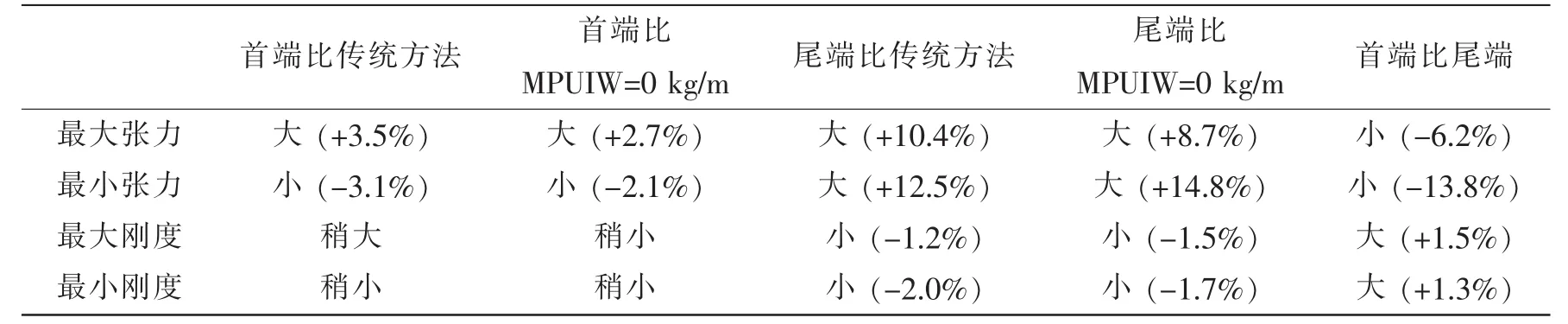
表3 系缆自重对计算结果的影响Tab.3 The cable's weight effects to the results

图8、图9和图10分别为系缆首端、尾端张力和动刚度值的计算结果。因系缆单位长度浮力大于重力，自身重量对尾端的影响较大，对上端点处影响略小，表3为计算结果的比较。系缆自身重量对动张力的总体影响较大，将其忽略会带来较大的计算误差，损失计算精度。

图8 系缆自重对首端张力的影响Fig.8 The weight's effects to the upper node's tension

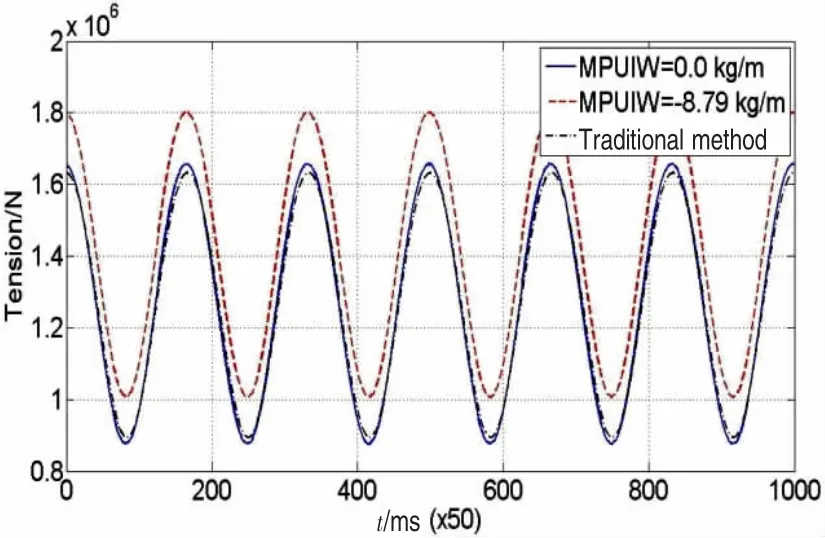
图9 系缆自重对尾端张力的影响Fig.9 The weight's effects to the lower node's tension

6 海流的影响

图10 系缆自重对动刚度值的影响Fig.10 The weight's effect to the dynamics stiffness

本文考虑非均匀海流对绷紧式系泊线动力学性能的影响，在考虑到系缆自重的情况下采用分段动刚度计算系缆动张力。节点所处位置的流函数为：J（z）=1.0× （sinθJi+cosθJj+0k ）（1. 0-z/150 ）m/s，z为节点所处的水深，θJ为流向。设流向为90°（沿x轴正方向），水面流速为2.0 m/s。

将系缆首尾两端动张力与无流时的比较，首端最大张力小0.55%，最小张力大0.70%，尾端最大张力小0.44%，最小张力大0.22%。尽管海流对系缆动张力的影响较小，但若能在计算中加入该部分的作用，计算精度将有增无减。

7 用统计方法计算缆段的平均张力

以上计算建立在系缆平均张力为定值的假设下，即假设平台在平衡位置附近做简谐运动，系缆平均张力即为预张力，其大小为1 278.0 kN。然而，在流体拖曳力、缆索自身重量和海流作用下，缆索不同分段的平均张力是不相同的，同一分段上平均张力也随着时间变化。这样平均张力将无法通过计算直接得到。于是，本文提出采用分段动刚度计算时，记录每一缆段在过去一段时间内的动张力值，并取该记录的平均值作为该缆段的平均张力，并将其用于该缆段的动刚度和动张力计算。

图11 用统计方法得到系缆平均张力Fig.11 The mean load using statistical method

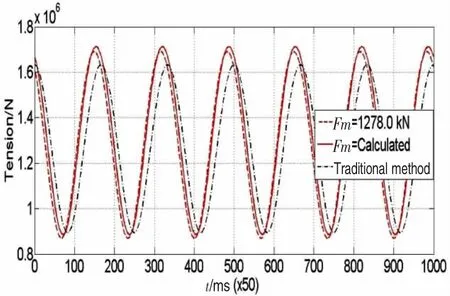
图12 首端动张力时间历程Fig.12 Variation with time of the upper node's tension

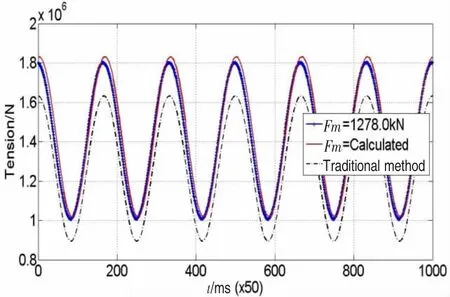
图13 尾端动张力时间历程Fig.13 Variation with time of the lower node's tension

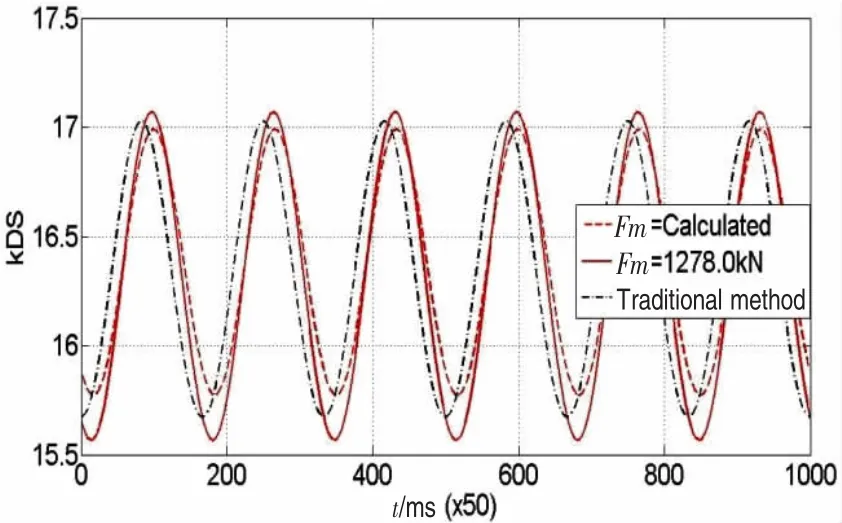
图14 首端动刚度时间历程 Fig.14 Variation with time of the upper node's dynamic stiffness

图11为统计得到的系缆首尾两端的平均张力，可以看出统计得到的缆段平均张力随时间波动，其大小要比定值1 278.0 kN大很多，这显然会对系缆动张力和动刚度的计算产生影响。图12和图13分别为采用统计方法计算缆段平均张力时，首尾两端节点动张力的计算结果，图14和图15分别为系缆首尾两端处动刚度值的计算结果，表4为计算结果与之前方法的比较，可以看出采用统计平均张力得到的计算结果相比于采用定值时，首尾两端的最大和最小张力都有所增大。最终计算结果显示，首端最大张力比传统方法大4.9%，最小张力比传统方法小1.1%，尾端最大张力比传统方法大12.2%，最小张力比传统方法大13.8%。