重载铁路牵引网雷击仿真模型比较研究

龙 林，黄 翰，何 月

0 引言

铁路运输是当代大容量重载货运较为经济实用的运输方式，保证铁路的安全稳定、可靠经济运行具有重要意义。而受雷电天气影响，雷电导致牵引变电所频繁跳闸、绝缘子大片破坏进而导致重载铁路故障，威胁货运铁路的正常安全运行。重载铁路供电系统中遭受雷击的部分主要为牵引网，牵引网对于重载铁路的可靠运行起着至关重要的作用，搭建重载铁路牵引网仿真模型对重载铁路系统雷击故障研究具有重要意义[1，2]。

围绕牵引网仿真模型搭建，目前已有相关学者做了大量的工作。文献[3]利用PSCAD/EMTDC丰富的模型库对带回流线的直接供电方式和高速铁路AT供电方式进行仿真。文献[4，5]对众多牵引网的仿真模型进行了总结与分析，提出仿真分析的主流倾向于通过数学模型编程实现。文献[6]利用Matlab/Simulink建立了高速铁路AT牵引供电系统的仿真模型，但模型不够完善，不能完整地展现AT牵引网的所有特性。文献[7]利用贝杰伦模型，通过在PSCAD软件中手动输入导线参数模块，以高速铁路AT供电方式下牵引网的几何结构作为研究对象进行建模。

上述所有建模方式均是考虑高速铁路AT供电方式下搭建牵引供电系统雷击仿真模型。而雷击对于重载铁路正常运行同样具有威胁和破坏性，上述建模未考虑搭建重载货运铁路牵引供电系统雷击仿真模型。本文利用PSCAD/EMTDC仿真软件中的互耦合线路（Mutually Coulped Wires）模型与贝杰伦（Bergeron）模型对重载铁路中运用较为广泛的带回流线的直接供电方式进行仿真，针对重载铁路牵引网搭建两种雷击仿真模型，通过比较仿真结果与理论数值，得出运用贝杰伦模型仿真重载铁路牵引网雷击故障更加准确。

1 重载铁路牵引网

重载铁路供电系统主要采用带回流线的直接供电方式，其供电系统主要由牵引变电所和牵引网组成，牵引变压器采用V-v接线方式。对于牵引网，主要由接触线、钢轨、回流线等构成牵引供电回路，将其称为悬挂系统（如图1所示），通过悬挂系统完成对电力机车的送电[8]。故在对牵引网进行仿真建模时，在不影响牵引网各导体的原始参数情况下，对悬挂系统进行合理等效和化简至关重要。

图1 牵引网悬挂系统

2 雷电流模型

由于在众多雷电流模型中，双指数函数模型和实测的雷电流波形最为接近，故本文采用双指数函数模型对雷电流波形进行仿真。双指数函数模型数学表达式为

式中：I为雷电流幅值，kA；α、β为时间常数，s。

在PSCAD/EMTDC元件库中选用对应的元件搭建雷电流模型，如图2所示。模型选用双指数函数波形模拟受控电流源波形，仿真模型中电流幅值为50 kA，波头时间为2.6 μs，波尾时间为50 μs，

图2 雷电流模型

在PSCAD/EMTDC中仿真标准雷电流波形如图3所示。

图3 标准雷电流波形

3 仿真结果比较

本文首先利用PSCAD/EMTDC对带回流线的直接供电方式的牵引供电系统正常和雷击故障两种情况进行仿真，系统仿真时间设置为2 s。牵引网长度L= 21 km，且每7 km长度的牵引网封装为一个模块，电力机车等效为交流电流源。

3.1 正常无雷击仿真结果比较

在正常无雷击情况下，分别采用互耦合模型和贝杰伦模型进行仿真，整体仿真模型如图4所示。通过仿真可得变压器出口处即接触线首端电压Ecup波形如图5所示。

图4 正常无雷击系统仿真模型

图5 接触线首端电压Ecup波形

根据上述仿真结果可知，互耦合模型接触线首端电压Ecup稳定值为39.35 kV，贝杰伦模型接触线首端电压Ecup稳定值为39.31 kV，接触线首端电压理论值为二者基本相符。

通过上述正常无雷击的两种模型仿真，可得变压器出口处即接触线首端电流Icup、回流线首端电流Ifup、钢轨首端电流Irup、承力索首端电流Imup仿真波形分别如图6～图9所示。

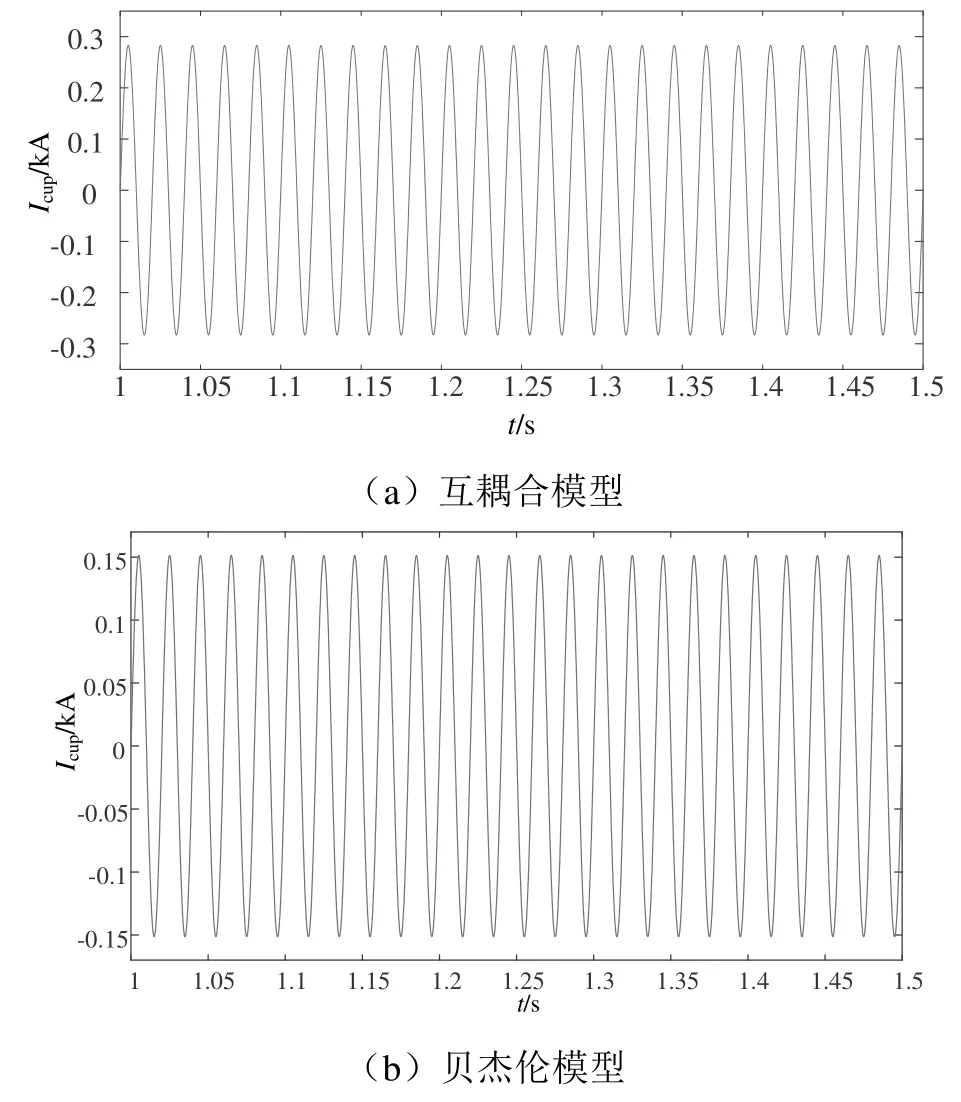
图6 接触线首端电流Icup波形

图7 回流线首端电流Ifup波形

图8 钢轨首端电流Irup波形

图9 承力索首端电流Imup波形

由上述仿真波形结果可知，受整个系统电容参数的影响，接触线首端电流Icup、回流线首端电流Ifup、钢轨首端电流Irup、承力索首端电流Imup均在仿真开始1 s后趋于稳定并不再呈现波动的趋势。互耦合模型接触线首端电流Icup、回流线首端电流Ifup、钢轨首端电流Irup稳定值分别为0.28、0.08、0.20 kA。贝杰伦模型接触线首端电流Icup、回流线首端电流Ifup、承力索首端电流Imup稳定值分别为0.151、0.301、0.2 kA。互耦合模型中钢轨首端电流Irup和回流线首端电流Ifup方向均与接触线首端电流Icup方向相反，并且Irup与Ifup之和等于Icup。贝杰伦模型中接触线与承力索共同传递电流，接触线首端电流Icup和承力索首端电流Imup方向相同，且二者电流方向均与回流线首端电流Ifup方向相反。仿真结果符合带回流线直接供电方式的重载铁路供电系统的电流分布，综合两种模型接触线首端电压和电流的仿真结果可见所建立仿真模型基本正确。

3.2 雷击故障仿真结果比较

在雷击情况下，同样采用互耦合雷击模型和贝杰伦雷击模型进行仿真，通过多次改变雷电流幅值与雷击接触线位置可得变压器出口处即接触线首端电压Ecup，接触线首端电流Icup，接触线末端电流Icend仿真波形。

t= 1.5 s时刻，在接触线14 km处加入幅值I=50 kA的标准雷电流，接触线首端电压Ecup、接触线首端电流Icup、接触线末端电流Icend、雷电流Surge仿真波形分别如图10～图13所示。

图10 接触线首端电压Ecup波形

图13 雷电流Surge仿真波形

由图10仿真结果可知，在雷击故障发生前后，两种模型下的接触线首端电压Ecup均维持在正常无雷击情况下的稳定值。对于互耦合模型，发生雷击故障时，接触线首端电压Ecup在雷击时出现高达429 kV的雷击过电压。对于贝杰伦模型，发生雷击故障时，接触线首端电压Ecup发生突变，出现高达104 kV雷击过电压。

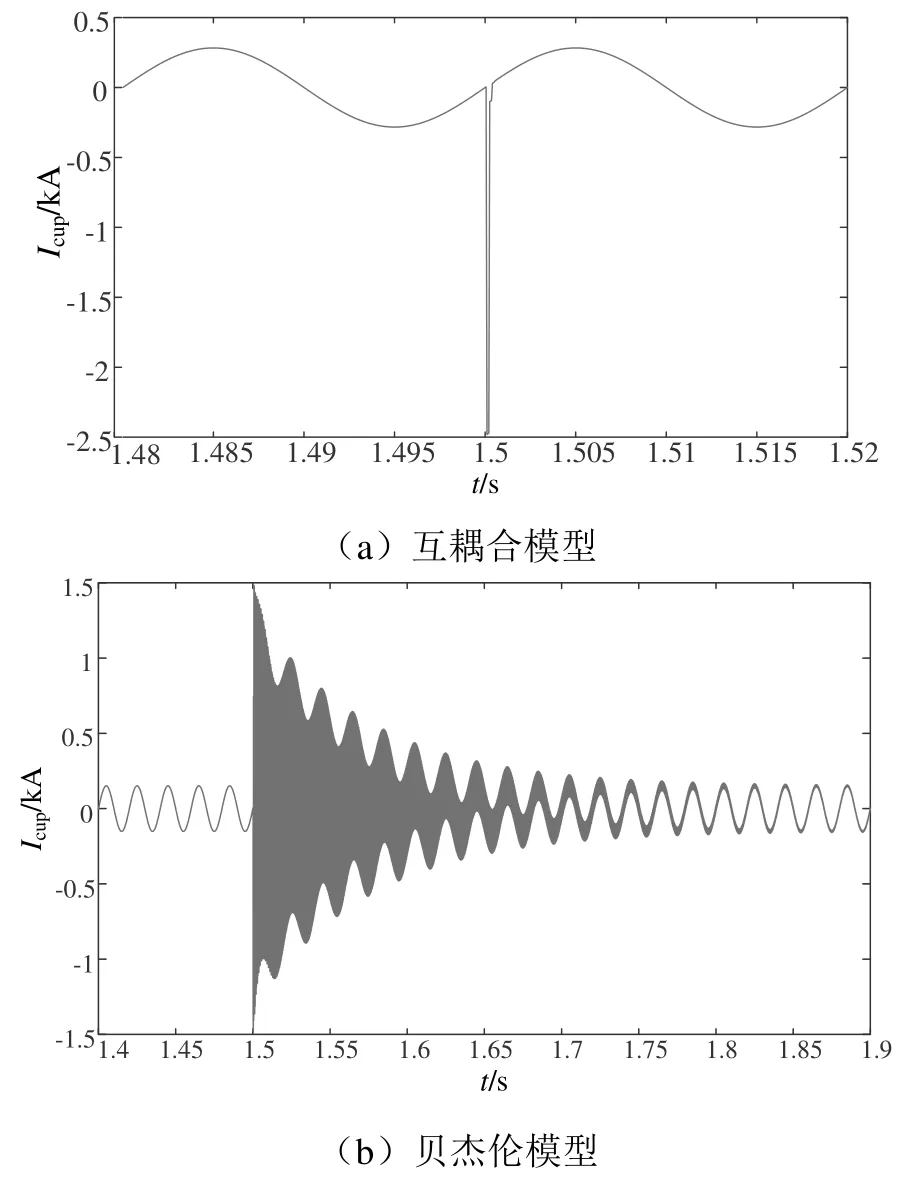
图11 接触线首端电流Icup波形

图12 接触线末端电流Icend波形

比较仿真结果可知，在雷击故障前，两种模型下的接触线首端电流Icup与接触线末端电流Icend均维持在正常稳定值，发生雷击故障时，互耦合模型中接触线首端电流Icup电流峰值突变为2.47 kA，而接触线末端电流Icend未出现突变特征。贝杰伦模型中接触线首端电流Icup电流峰值突变为1.45 kA，接触线末端电流Icend突变为1.252 kA。互耦合模型Icup突变值2.47 kA相对于雷电流仿真波形峰值2.48 kA基本保持不变，说明损耗较小，而接触线末端电流Icend并未出现突变特征。贝杰伦模型中Icup峰值1.45 kA，Icend峰值1.252 kA相对于雷电流仿真波形峰值2.48 kA具有明显的损耗和衰减。

t= 1.5 s时刻，在接触线7 km处加入幅值I= 50 kA的标准雷电流，接触线首端电压Ecup、接触线首端电流Icup、接触线末端电流Icend波形分别如图14～图16所示。

图14 接触线首端电压Ecup波形

图16 接触线末端电流Icend波形

通过改变雷击接触线位置，由上述仿真结果可知，当雷击接触线7 km处时，在雷击故障发生前后，与雷击接触线14 km处时相同，两种模型下的接触线首端电压Ecup均维持在正常无雷击情况下的稳定值。对于互耦合模型，发生雷击故障时，接触线首端电压Ecup在雷击时出现高达480.7 kV的雷击过电压。对于贝杰伦模型，发生雷击故障时，接触线首端电压Ecup发生突变，出现高达99 kV雷击过电压。

图15 接触线首端电流Icup波形

当雷击接触线7 km处，由上述仿真结果可知，两种模型下的接触线首端电流Icup与接触线末端电流Icend在雷击之前均维持在正常稳定值，发生雷击故障时，互耦合模型中接触线首端电流Icup峰值突变为2.476 kA，而接触线末端电流Icend未出现突变特征。贝杰伦模型中接触线首端电流Icup峰值突变为1.3 kA，接触线末端电流Icend突变为1.257 kA。互耦合模型Icup突变值2.476 kA相对于雷电流仿真波形峰值2.48 kA与雷击接触线14 km处类似基本保持不变，说明损耗较小，而接触线末端电流Icend同样并未出现突变特征。而贝杰伦模型中Icup峰值1.3 kA，Icend峰值1.257 kA，相对于雷电流仿真波形峰值2.48 kA具有明显的损耗和衰减。

t= 1.5 s时刻，在接触线14 km处加入幅值为30 kA的雷电流，接触线首端电压Ecup、接触线首端电流Icup波形、接触线末端电流Icend、雷电流Surge仿真波形如图17～图20所示。

图17 接触线首端电压Ecup波形

图20 雷电流Surge仿真波形

通过改变雷电流幅值，当雷电流幅值I= 30 kA时，对于互耦合模型，发生雷击故障时，接触线首端电压Ecup在雷击时出现高达356 kV的雷击过电压。对于贝杰伦模型，发生雷击故障时，接触线首端电压Ecup发生突变，出现高达78 kV雷击过电压。可见，相对于相同雷击点雷电流幅值I= 50 kA的突变值，改变雷电流幅值后两种模型下的雷击过电压均有所减小。

图18 接触线首端电流Icup波形

图19 接触线末端电流Icend波形

当雷电流幅值I= 30 kA时，由仿真波形图可知，互耦合模型中接触线首端电流Icup电流峰值突变为1.48 kA，相对于雷电流幅值I= 50 kA下的Icup突变值2.47 kA明显减小，接触线末端电流Icend同样保持稳定，未出现突变特征。贝杰伦模型中，接触线首端电流Icup电流峰值突变为0.84 kA，相对于雷电流幅值I= 50 kA情况下的Icup突变值1.45 kA同样明显衰减，接触线末端电流Icend突变为1.257 kA具有与Icup相同的衰减特征。

综合以上仿真结果，互耦合模型是模拟单位长度下3条相互耦合的导体模型，是以输入导体自电阻、自电感以及导体之间的互电感的形式表征集中参数进而仿真。通过改变雷击接触线的不同位置、不同雷电流幅值后，仿真接触线首端电压Ecup和电流Icup、接触线末端电流Icend发现，互耦合模型表征雷电流在牵引网导体内传导时的损耗特性较弱、准确性较低，且无法表征雷电流在接触线末端的故障特性，更无法充分准确表征导体之间的电磁互耦合关系。而在电磁暂态模型中主要包括贝杰伦模型、JMarti模型、Semlyen模型，由于牵引网跨距较短且本文主要考虑雷击重载铁路牵引网，故采用贝杰伦模型对其建模。贝杰伦模型采用分布式LC参数和集总电阻的行波线路模型，是以分布式方式来代表PI段的L和C元件，同样仿真接触线首端电压Ecup和电流Icup、接触线末端电流Icend发现，雷电流传导至接触线首端和末端时，Ecup、Icup和Icend突变值相对互耦合模型较小且损耗较大，说明在贝杰伦模型下，表征雷击后各电气量特性更为准确，可以更好地表征重载铁路牵引网各导体之间的电磁耦合关系及雷电流在牵引网中的衰减特性。

4 结论

本文利用PSCAD/EMTDC搭建了重载铁路系统正常和雷击故障两种状态下的仿真模型。通过比较正常情况下互耦合模型与贝杰伦模型仿真电气量与理论值发现，二者模型均是基本正确的。在比较雷击故障情况下互耦合雷击模型与贝杰伦模型发现，虽然互耦合模型能够表征牵引网各导体之间的部分电磁互耦合关系，但相对于贝杰伦雷击模型仿真而言，贝杰伦模型在仿真雷击故障时能够更好地表征重载铁路牵引网各导体之间的电磁耦合关系及雷电流在牵引网中的衰减特性。在对重载铁路进行牵引网雷击故障仿真研究时，运用贝杰伦模型作为悬挂系统导线模型，对重载铁路牵引网几何结构进行建模具有更好的仿真效果和参考价值。