超大型浮体柔性夹层连接器力学性能研究
2019-03-14祁恩荣李志伟夏劲松
张 浩,祁恩荣,宋 恒,李志伟,夏劲松
(1.中国船舶科学研究中心,江苏 无锡 214082;2.江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003)
0 引 言
在海洋工程领域超大型浮体的研发工作一直以来都是世界各国的研究重点,无论从政治、军事、社会和经济层面,超大型浮体都具有极其重要的战略意义[1-3]。而连接器作为超大型浮体最薄弱的环节,势必成为该项研究的热点问题。其中,连接器的力学性能不仅决定了连接器的安全问题,更影响着整个超大型浮体的可靠性。因此,本文提出来一种具有柔性夹层的连接器,并针对该连接器进行力学性能分析,通过对比不同参数的柔性夹层获得连接器的力学参数,为今后超大型浮体连接器的设计提供数据参考。
Riggs等人[4]给出了不同刚度的连接器对多浮体模块的运动响应的影响,并研究了在不同刚度连接器连接情况下,阻尼与波浪参数变化对多浮体模块的运动响应的影响。Riggs等人[5-6]针对多模块半潜式浮体进行研究,研究结果表明:多模块半潜式浮体的模态对连接器载荷影响较大,连接器的布置形式对于浮体的运动响应影响显著,同时连接器的阻尼要比辐射阻尼更为显著。此外,Riggs等人还给出了一种多模块浮体运动响应的近似求解方法。Derstine等人[7]为降低连接器所承受的载荷,提出了一种采用高弹性管材的顺从式连接器概念,基于该设想分别设计了4自由度和6自由度两套顺从式连接器。Ramsamooj等人[8-9]提出来一种疲劳寿命计算模型,并将其应用于移动浮式基地的连接器的疲劳寿命的计算中,同时获得了某移动浮式基地连接器的疲劳可靠性。Riyansyah等人[10]以最小化两浮体水弹性响应为目标,基于频域分析手段提出了一种连接器优化设计方法,并获得了最优的连接器布置形式和转动刚度,同时分析获得了不同连接器刚度对两浮体系统水弹性响应的影响。
祁恩荣等人[11]针对三模块超大型浮体建立了刚性模块柔性连接器模型,结合势流理论计算得到了连接器的动力响应,并给出了浅水效应可以导致连接器荷载增大的结论。丁伟等人[12]在国内首次实现了多模块超大型浮体的水池模型试验,并给出了详细的试验流程和方案,通过试验与理论计算,给出了不同刚度连接器在不同作业工况下的荷载值。李润培等人[13-16]利用刚性模块柔性连接器模型建立多模块超大型浮体水动力模型,假定连接器为线性弹簧模型,利用三维势流理论进行整体动力计算,并给出了连接器的动态载荷。谷家扬[17]给出了一种针对超大型浮体连接器荷载的时域计算方法,并对比了不同浪向角对连接器荷载的影响。
结合超大型浮体的连接需求,本文提出一种具有柔性夹层的铰接式连接器,通过建立钢与柔性夹层的层合本构模型可以有效地减少接触问题的单边约束不等式数量,提高计算收敛性。通过采用接触力学相关理论,可以获得该种具有柔性夹层的铰接式连接器的力学性能,并获得不同柔性夹层参数对这一性能的影响程度,从而为日后的连接器设计工作提供技术与数据支持。
1 计算理论
1.1 具有柔性夹层的层合本构模型
铰接式连接器由单耳、双耳、钢轴和柔性夹层四部分组成,如图1所示。该连接器通过柔性夹层与钢轴的变形实现各自由度的刚度控制,通过添加不同厚度和材料的柔性夹层可以明显改变结构的刚度和各构件的应力水平,以保证连接器刚度和应力均处于合理水平,确保整个超大型浮体的完整性。
由于铰接式连接器中接触问题较多,严重影响计算的收敛性,根据计算经验发现,如果将柔性夹层与铰接式连接器通过直接接触的办法进行计算,其计算模型难以收敛,且计算效率极低,为提高模型计算效率并简化建模过程,本文将柔性夹层与钢轴视为层合本构模型[18],通过在接触面粘结节点实现对柔性夹层与钢轴间接触问题的简化,从而减少单边约束问题数量,提高计算效率和收敛性,具体的本构模型如图2、3所示。
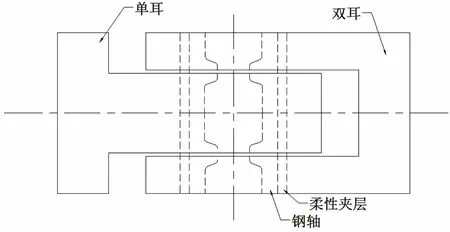
图1 具有柔性夹层的铰接式连接器Fig.1 Connector with flexible sandwich
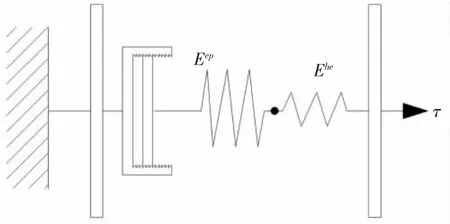
图2 具有柔性夹层的层合本构模型Fig.2 Laminating constitutive model of connector with flexible sandwich
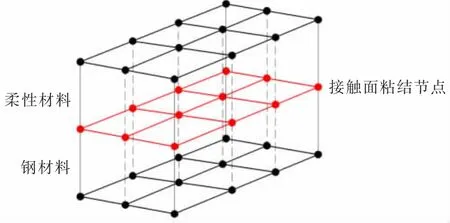
图3 接触面处的节点粘结Fig.3 Common nodes in contact surface

式中:εep为弹塑性单元的应变,τep为弹塑性单元的应力,Eep为弹塑性单元的弹性模量,εhe为超弹性弹性单元的应变,τhe为超弹性单元的应力,Ehe为超弹性单元的弹性模量,同时Ehe随着材料的变形而变化。
1.2 超弹性模型
该铰接连接器的柔性夹层为尼龙或橡胶,尼龙材料采用弹塑性本构模型,这里不再赘述,橡胶采用超弹性本构模型来描述其力学行为。根据连续介质力学理论,认为橡胶是各向同性材料,可采用应变能表征[19-21],即Polynomial Form模型,其表示形式如下:
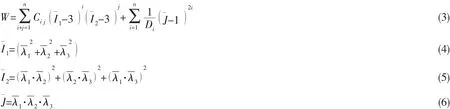
对于常用描述橡胶超弹性本构关系的模型有Mooney-Rivlin模型,Neo-Hookean模型,Ogden模型和Yeo模型等。其中Mooney-Rivlin模型即为Polynomial Form模型中n=1时的简化形式。

Neo-Hookean模型可看作是Polynomial Form模型中n=1,C01=0时的特殊形式:

式中:μ0为超弹性材料的初始剪切模量[21]。
Ogden模型采用主方向的应变率进行表征,其具体形式如下[22-23]:

式中:μi和αi为为试验待测定参数,通常设定μi·αi>0以保证模型稳定。
Yeoh模型可以看作是Polynomial Form模型中n=3,C01=0时的特殊形式[24]:

1.3 接触计算
接触问题是在外加荷载作用下,相互接触的物体产生局部变形和应力的问题。接触问题存在诸多非线性特性,即接触压力分布的非线性,接触区域变化非线性,摩擦引起的非线性以及材料塑性变形引起的非线性等[25]。接触问题为单边不等式约束的平衡问题,其求解方法为反复迭代搜索准确的接触状态,具体平衡方程见(12)式,变形协调方程见(13~14)式[26]。

式中:Q为载荷,p为接触应力,Ac为接触区域,δ为弹性趋近量,Z为初始间距,E为杨氏模量,υ为泊松比。
国内外对于接触问题的理论研究已经有诸多相关成果,如Hertz弹性接触理论等。但这些接触理论只能求解一些较为简单的接触问题,简化假设较多,局限性较大。随着计算机技术的发展,以有限元为核心的CAE仿真技术成为了解决接触问题的主流方法。目前较为常用的接触计算方法有传递矩阵法,间隙有限元法,罚函数法和拉格朗日法等,本文采用罚函数法进行计算。
根据能量最小化原理,接触问题是一个通过寻求唯一接触状态以达到系统势能最小化问题。

式中:Π为系统势能,g为接触间隙。
通过引入罚函数的附加泛函,可以将(15)式的约束极值化问题转化为下述的无约束极值化问题。通过选取适当大小的惩罚因子,可以达到较好的计算精度,同时避免病态方程的产生。

式中:Ep为惩罚因子,P为嵌入深度。
2 复合材料层合本构模型与接触计算方法的对比分析
具有柔性夹层铰接式连接器存在多个接触问题,包括单双耳之间的接触,单双耳与柔性夹层的接触,柔性夹层与钢轴的接触。由于接触问题具有强非线性,在计算过程中收敛性很差,同时计算效率较低,为解决这一问题并得到理想效果,本文将柔性夹层与钢轴作为复合材料层合本构模型,为验证这一假设的准确性,现对两接触平板进行两种方法的验证性计算。
针对上述问题,本文提出一个两接触平板模型,用以验证复合材料层合本构模型与接触计算之间的相似关系,模型具体参数见表1。

表1 两接触平板基本参数Tab.1 Parameters of two plates
通过对比计算发现,采用复合材料层合本构模型和接触计算两种方法所得的结果相差不大,具体计算结果如图4~7所示,统计结果见表2。
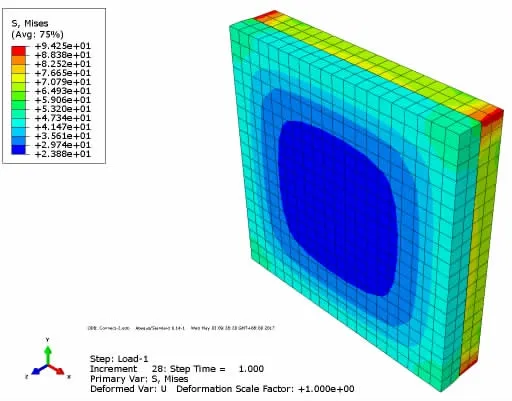
图4 50 MPa压强下接触计算结果(应力)Fig.4 Results of plates by connect method in 50 MPa pressure(stress)
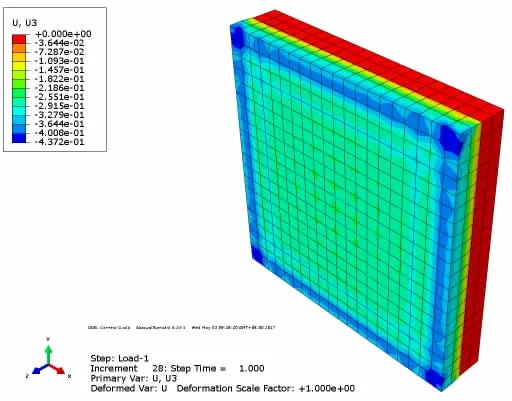
图5 50 MPa压强下接触计算结果(法向位移)Fig.5 Results of plates by connect method in 50 MPa pressure(normal displacement)
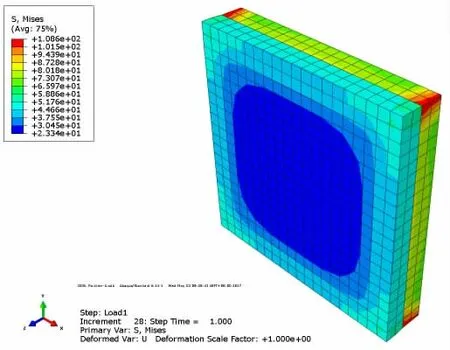
图6 50 MPa压强下复合材料层合模型计算结果(应力)Fig.6 Results of plates by laminating constitutive model in 50 MPa pressure(stress)
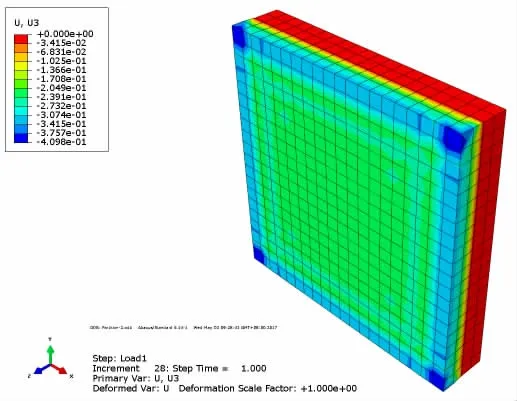
图7 50 MPa压强下复合材料层合模型计算结果(法向位移)Fig.7 Results of plates by laminating constitutive model in 50 MPa pressure(normal displacement)

表2 对比计算结果统计Tab.2 Contrast of two methods
通过对比两种计算方法所得结果,发现采用复合材料层合本构模型与接触计算所得结果相差很小,各项指标计算误差在2%~15%之间,且两接触板的应力分布关系基本一致,可以根据实际情况采用该方法代替一部分接触问题的计算。
3 模型试验对比分析
为进一步验证采用复合材料层合本构模型的方法的准确性,本文设计连接器的模型试验,并进行计算与实验结果的对比验证。试验模型为设计连接器的1:10缩比模型,如图8所示。通过进行极限强度试验,获得试验模型的荷载位移曲线以及失效形式,如图9所示。并以此为基础,进行计算理论的对比验证。

图8 连接器实验模型及加载系统Fig.8 Model of connector and loading system

图9 试验模型的失效形式Fig.9 Failure mode of experimental model
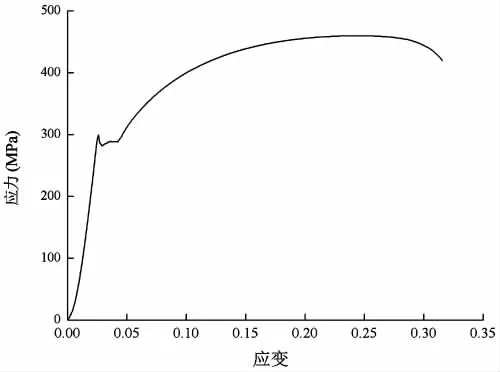
图10 钢材料参数曲线Fig.10 Material parameter of steel
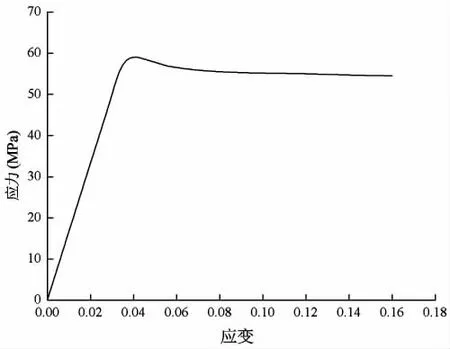
图11 尼龙材料参数曲线Fig.11 Material parameter of nylon
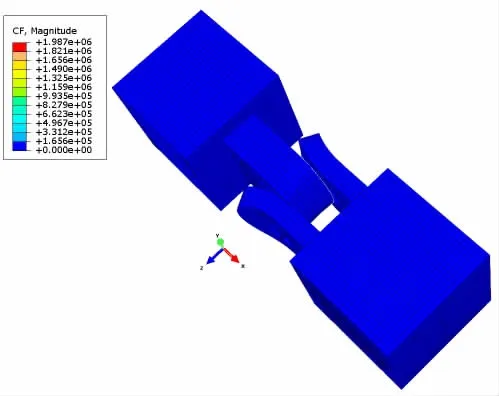
图12 计算获得的失效形式与极限强度Fig.12 Failure mode and ultimate strength of FEM
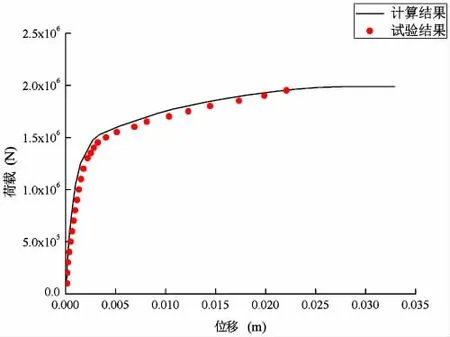
图13 荷载位移曲线对比Fig.13 Contrast of load-displacement curve
基于上述计算理论,输入材料参数,如图10~11所示,其中柔性夹层采用尼龙进行计算[27],获得连接器变形情况,如图12所示。通过对比试验模型与计算模型各部件的变形情况,发现计算结果与实验结果基本一致,同时分别获得计算模型与实验模型的荷载位移曲线,如图13所示。可知,计算得到连接器的极限强度为1 987 kN,而实验得到连接器的极限强度在1 950~2 000 kN之间,说明了计算理论的准确性。
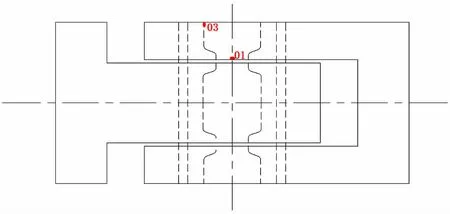
图14 连接器纵向两测点位置图Fig.14 Location of measuring point of connector in length direction
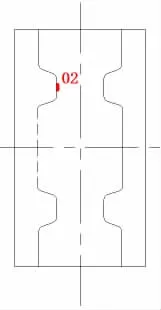
图15 钢轴横剖面测点位置图Fig.15 Location of measuring point of axis in transverse cross section
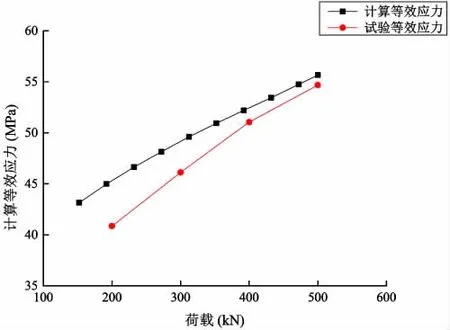
图16 第01号测点有效应力对比Fig.16 Contrast of effective stress on 01 node
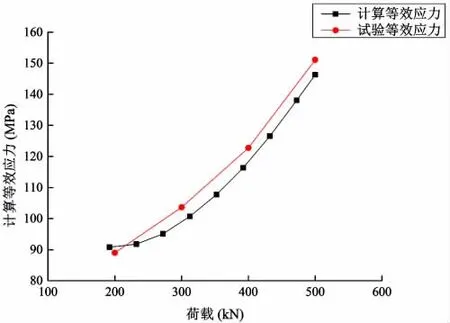
图17 第02号测点有效应力对比Fig.17 Contrast of effective stress on 02 node
为进一步说明上述计算理论及方法的准确性,现将计算结果与试验测点所得结果进行对比,提取试验过程中三个主要测点的实验数据,分别进行弹性阶段与塑性阶段的结果对比,测点位置如图14~15所示。
分别提取上述三个测点在弹性阶段的试验应变值,进行有效应力的换算,并与计算结果进行对比,如图16~18所示。对比结果显示,根据上述复合材料层合本构模型理论方法所得的主要测点在弹性阶段时有效应力与试验结果基本一致。

图18 第03号测点有效应力对比Fig.18 Contrast of effective stress on 03 node
再次提取破坏前图14~15所述主要测点的应变量,其计算应变与实测应变值统计结果见表3,发现计算结果与试验结果差别不大。综合考虑弹性阶段与塑性阶段理论计算与试验所得结果基本吻合,进一步证明了上述计算理论的准确性。

表3 计算应变与实测应变对比Tab.3 Contrast of computing and test strain
4 不同材料参数对连接器力学性能的影响
为进一步研究连接器力学性能对柔性夹层材料参数的敏感程度,本文分别考虑不同厚度的柔性夹层,以及不同弹性模量和泊松比的尼龙和橡胶材料对于连接器力学性能和轴向刚度变化的影响,材料参数分布情况见表4。
通过计算分析发现,橡胶和尼龙夹层对于连接器钢轴应力分布影响差异较大。由于尼龙较硬,可以承担更多的外载荷,使得钢轴侧面的压应力较小,进而钢轴整体应力水平较低,计算结果如图19~20所示。
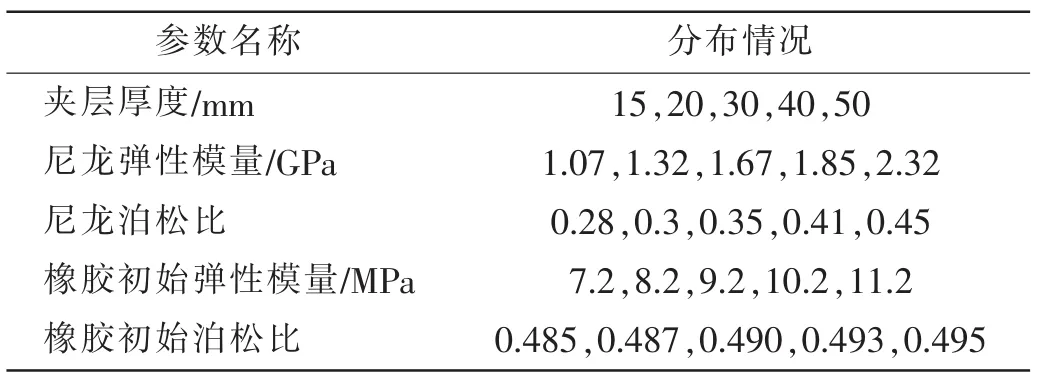
表4 柔性夹层基本参数Tab.4 Parameter of flexible sandwich

图19 带有橡胶夹层的应力分布Fig.19 Stress of connector with rubber sandwich

图20 带有尼龙夹层的应力分布Fig.20 Stress of connector with nylon sandwich
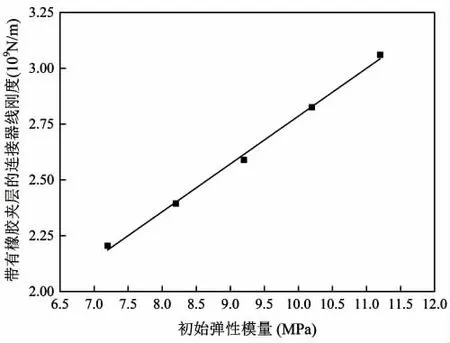
图21 不同初始弹性模量对连接器刚度的影响(橡胶)Fig.21 Effect of initial elastic modulus on stiffness of connector(Rubber)

图22 不同弹性模量对连接器应力的影响(尼龙)Fig.22 Effect of elastic modulus on stress of connector(Nylon)
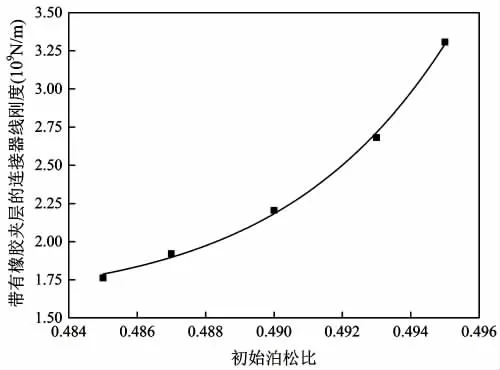
图23 不同初始泊松比对连接器刚度的影响(橡胶)Fig.23 Effect of initial Poisson's ratio on stiffness of connector(Rubber)
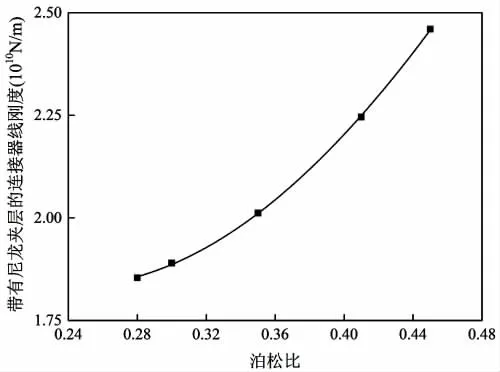
图24 不同泊松比对连接器应力的影响(尼龙)Fig.24 Effect of initial Poisson's ratio on stress of connector(Nylon)
通过控制变量,分别获得不同初始弹性模量,泊松比和夹层厚度条件下连接器轴向刚度变化情况,如图21~25所示。由图中可以看出,连接器轴向刚度对上述参数非常敏感,柔性材料的初始弹性模量和泊松比增大,会使连接器轴向刚度明显增大,柔性材料厚度增大会使连接器轴向刚度明显降低。
由图21~24可知,连接器轴向刚度与柔性材料的初始弹性模量呈线性变化关系,与泊松比呈指数变化关系。通过对比图25中两条曲线可知,采用尼龙夹层的连接器轴向刚度要强于采用橡胶夹层的连接器,且两种柔性夹层的连接器刚度随厚度的变化趋势基本一致。结合图19~20可知,橡胶和尼龙夹层对于改变连接器力学性能各有特点,采用尼龙夹层可以较好地控制连接器的应力水平,避免局部位置提前进入塑性,但由于尼龙夹层的连接器轴向刚度较强,结合多模块超大型浮体水动力相关研究成果可知[11],刚度较强时,连接器受到的外载荷同样可能增大,故夹层的材料参数的选取是控制连接器应力水平的双因素问题,工程应用过程中,应针对具体情况进行柔性夹层材料参数的优化才能较好解决这个问题。
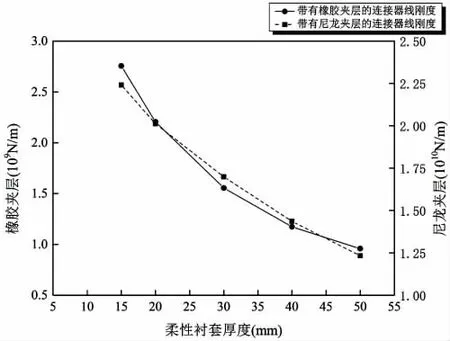
图25 不同初始厚度对连接器刚度的影响Fig.25 Effect of initial thickness on stiffness of connector
5 结 语
(1)本文将复合材料层合本构模型与接触力学相结合,较好地解决了复杂接触问题收敛性差的问题,并提高建模与修改模型的效率,与试验数据对比验证其理论的正确性,同时获得良好计算结果,可作为今后类似研究工作的方法参考。
(2)通过控制变量,发现柔性夹层的初始弹性模量、泊松比和厚度对于连接器的轴向刚度均有明显影响,并得到了连接器轴向刚度随各参数的变化趋势。
(3)通过分析发现,柔性夹层对于铰接式连接器的轴向刚度影响显著,同时柔性夹层参数不同,也会影响连接器的应力水平,选用柔性夹层时,虽然可以降低连接器的轴向刚度进而避免浮体模块对连接器产生较大外载荷,但也提高了连接器的应力水平。因此选取柔性夹层时,需要针对这一矛盾体进行优化分析。
