钛合金耐压结构蠕变数值计算方法与试验验证
2019-03-14黄进浩张爱锋万正权
王 雷 , 屈 平 , 黄进浩 , 张爱锋 , 万正权
(1.中国船舶科学研究中心,江苏 无锡 214082;2.深海载人装备国家重点实验室,江苏 无锡 214082)
0 引 言
蠕变是材料在恒定应力作用下,应变随时间的延长而增长的流变现象。与传统的塑性变形不同,蠕变在应力小于材料屈服极限时也会出现[1-2]。钛合金在深海环境下会产生不同程度的蠕变变形[3]。与航空领域钛合金在高温下的中低应力拉伸蠕变现象不同[4],深海环境的钛合金耐压结构蠕变属于常温下的高应力压缩蠕变。深海高压下耐压结构局部高应力区域的应力会接近材料屈服强度,会产生明显的蠕变响应,进而蠕变应变对钛合金耐压结构的强度和稳定性会产生影响。由深海环境压缩载荷引起的、高应力下的蠕变应变是钛合金耐压结构安全性评估与计算的重要方面。
目前国内外对工程结构蠕变计算方法的研究已经取得了一定成果。Ankem等[5]基于幂次法则的蠕变本构方程对核废料箱保护罩开展了蠕变计算,认为Ti-6Al-4V合金在接近屈服极限的应力水平、持续10 000 h蠕变时间的情况下易于产生蠕变失效。刘学等[6]应用修正的Graham蠕变模型对P91钢在625℃下的不同应力水平进行了单轴蠕变过程的数值模拟,计算结果和实验数据吻合较好。蔡志勤等[4]对镍基合金的航空发动机涡轮叶片在980℃下单轴蠕变的全过程作了计算。苗克军等[7]采用θ概念投影法根据Graham蠕变模型对拉伸蠕变试验数据进行非线性拟合,对油膜轴承衬套巴氏合金进行了蠕变计算。现已有较多文献对高温结构在拉应力状态的蠕变计算方法进行了研究,但是针对常温高应力的钛合金耐压结构压缩蠕变尚未建立成熟的计算方法,适合深海环境下钛合金蠕变计算模型系数尚不明确。
本文对比分析多种典型蠕变本构模型,考虑应力水平、本构模型、蠕变时间等三个因素的影响,确定钛合金材料常温压缩蠕变本构方程及其系数,初步建立钛合金耐压结构蠕变数值计算方法,并以耐压结构蠕变试验进行验证。开展环肋圆柱壳结构的蠕变数值计算,给出蠕变前后模型的应力、应变和位移的变化情况,为钛合金耐压结构蠕变特性研究提供参考。
1 蠕变数值计算方法
基于ANSYS有限元软件的蠕变数值计算程序:
(1)创建目标结构的几何模型;
(2)对几何模型划分网格,定义单元属性;
(3)施加载荷与边界条件;
(4)设置求解控制选项,进行静力求解;
(5)提取蠕变前的结构应力、应变特征;
(6)选择蠕变本构方程,输入材料的蠕变系数和蠕变时间,设置加载方式和步长调节,进行蠕变求解;
(7)提取蠕变应变、蠕变变形以及蠕变后的结构应力、应变特征。
在上述的蠕变数值计算步骤中,蠕变本构方程的选取和蠕变系数的确定是蠕变分析的关键要素,决定了蠕变计算的方法适用性和结果准确度。本文对蠕变计算的本构模型进行梳理,给出每个模型特征和适用阶段。结合深海钛合金耐压结构的蠕变特点,初步选取几种典型的本构模型进行比较分析,对钛合金材料压缩蠕变试验数据进行非线性回归分析,将基于不同本构模型的蠕变数值计算结果与试验值进行对比,最终确定适用于深海钛合金耐压结构的蠕变本构模型及其系数。
2 耐压结构蠕变本构方程
应用有限元数值方法计算结构的蠕变特性具有求解速度快、计算成本低的特点,在工程领域有广泛的应用。ANSYS、ABAQUS、ADINA、MARC等大型商用有限元软件均有成熟的蠕变计算模块。
商用软件ANSYS的蠕变分析包括隐式蠕变模型和显式蠕变模型。显示蠕变分析的求解采用欧拉朝前法,每个子步内蠕变应变率为常数,不执行平衡迭代,计算精度较低。隐式蠕变分析计算时间较长,数据存储量大,收敛要求较高,计算结果误差小。对于需要很少时间步的情况适用于显示蠕变分析,隐式蠕变分析更精确,ANSYS提供的隐式蠕变本构模型有13个,如表1所示。

表1 ANSYS隐式蠕变本构方程Tab.1 Implicit creep constitutive equations of ANSYS
与ANSYS类似,有限元软件ABAQUS的蠕变计算主要包括两个部分:获得该结构材料的蠕变模型参数和建立蠕变分析步。ABAQUS提供的蠕变模型有三种,分别为时间强化模型、应变强化模型以及双曲正弦模型,其蠕变本构方程及特点如表2所示。

表2 ABAQUS蠕变本构方程Tab.2 Creep constitutive equations of ABAQUS
综合ANSYS和ABAQUS两种有限元软件的蠕变方程,基于表1和表2可以发现,双曲正弦模型(广义Garofalo模型)、指数模型和Norton模型认为蠕变应变率与时间无关,仅适用于蠕变应变呈线性变化的稳态蠕变阶段,不能完全描述深海钛合金耐压结构两个阶段的蠕变特点[8-9]。除此之外,其它形式的蠕变本构模型根据强化准则可分为两类:时间强化和应变强化,这两种本构方程均能描述初始蠕变阶段的蠕变特征。相比于以应变为主要特征变量的应变强化准则本构模型,时间强化准则更能凸显材料的蠕变应变随时间变化的特点,直观性更好。
时间强化和修正的时间强化本构方程均以时间和应力为表征蠕变的主要变量,时间强化模型可以看作修正的时间强化模型与Norton模型的叠加,不仅可以表征蠕变应变率不断减小的初始蠕变阶段,而且能够描述应变呈线性增加的稳态蠕变阶段。
广义Graham蠕变本构方程基于Graham&Walles数学模型,以指数多项式的形式对时间强化本构方程的时间项进行细化[10]。通过增加与时间相关的幂指数多项式系数,可以提升模型对蠕变应变率变化的适应性,同时考虑有限元法对变量的迭代要求。
由此可见,修正的时间强化模型、时间强化模型和广义Graham模型可以很好地描述初始蠕变阶段和稳态蠕变阶段的蠕变特征,本文初步选择这三种模型作为典型的钛合金压缩蠕变本构方程。
3 蠕变本构模型系数与试验验证
为了验证经过非线性回归分析的蠕变本构方程系数的正确性,开展环肋圆柱壳模型的蠕变试验,检测典型位置的蠕变应变,揭示钛合金耐压结构蠕变应变的分布特征和变化规律。蠕变试验系统由压力筒、加卸载系统、应变测量系统、数据采集系统和试验模型等组成。
蠕变试验模型采用TC4钛合金材料,在环材基础上精车加工而成。其结构形式为两端带有封板的环肋圆柱壳结构,由圆柱壳、肋骨、封板、加强筋等结构组成,其中环肋圆柱壳包括试验段和过渡段,结构如图1所示。模型试验段圆柱壳的长径比L/R=3.1,径厚比R/t=58.3。
将试验模型吊入压力筒内,向压力筒内注水至目标压力,保持压力不变,进行蠕变试验。在稳定的压力环境下,应用应变仪以间隔测量的方式记录测点应变随时间变化。模型在蠕变试验时间为1 960 h时,压力卸载至0,应变仪记录了该次模型测点的纵向和周向蠕变应变。
选择文献[8]中TC4ELI材料的压缩蠕变试验数据进行回归分析。蠕变本构模型系数的影响因素主要包括应力水平、本构模型、蠕变时间等三个方面,下面针对这三个主要影响因素分别进行比较分析。
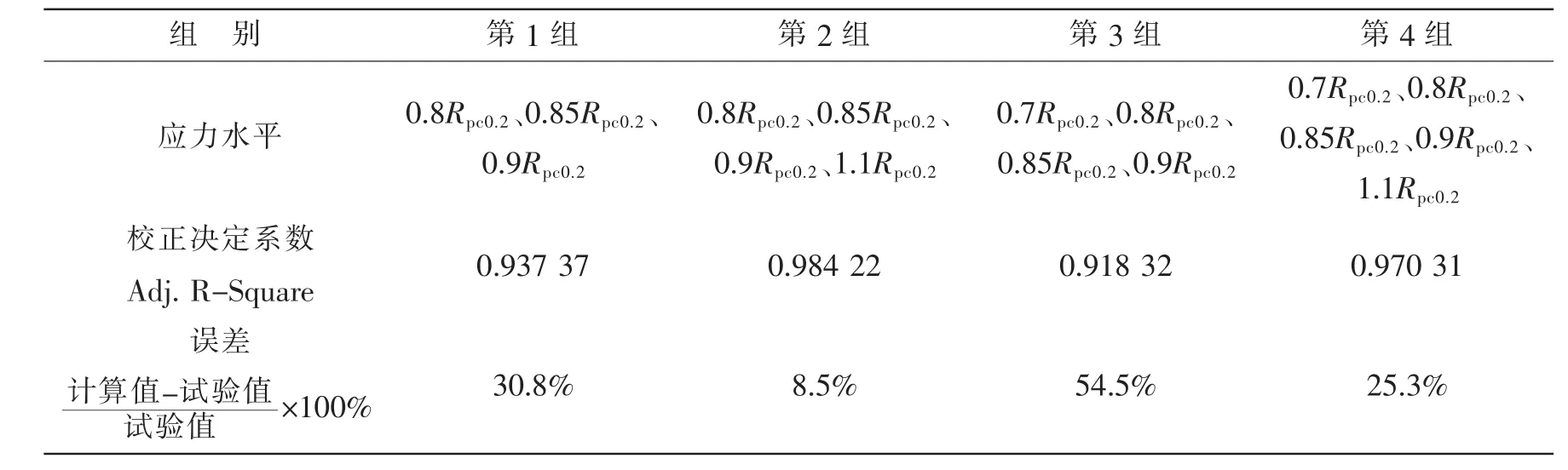
表3 不同应力水平的蠕变系数和蠕变应变Tab.3 Coefficients and strain of creep for various stress levels
(1)蠕变应力水平的影响
选取4组不同应力水平的蠕变数据进行拟合:第1组,0.8Rpc0.2、0.85Rpc0.2和0.9Rpc0.2三个应力水平;第 2 组,0.8Rpc0.2、0.85Rpc0.2、0.9Rpc0.2和 1.1Rpc0.2四个应力水平;第 3 组,0.7Rpc0.2、0.8Rpc0.2、0.85Rpc0.2和 0.9Rpc0.2四个应力水平;第 4 组,0.7Rpc0.2、0.8Rpc0.2、0.85Rpc0.2、0.9Rpc0.2和 1.1Rpc0.2五个应力水平。应用Origin数据分析软件将上述4组数据均以修正的时间强化模型为蠕变本构方程进行蠕变系数的非线性回归分析。以拟合得到的蠕变系数作为输入,对环肋圆柱壳模型进行蠕变数值计算,并与跨中位置纵向蠕变应变的试验值进行对比,误差如表3所示。
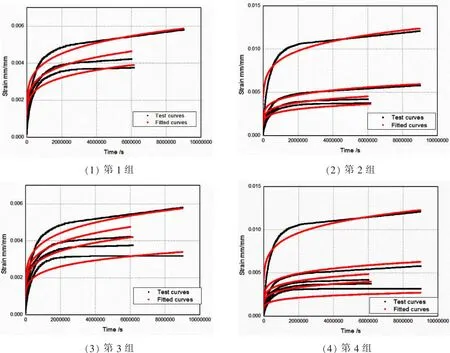
图2 不同应力水平的蠕变曲线拟合Fig.2 Fitting of creep curves for various stresses
将由0.8Rpc0.2、0.85Rpc0.2和0.9Rpc0.2三个应力水平组成的第1组作为参照组。第2组加入了1.1Rpc0.2这一应力水平的蠕变数据,使系数C1减小了一个数量级,该组的校正决定系数最大,拟合结果最好,同时蠕变应变的计算值也最接近试验值。第3组加入了未进入稳态阶段的0.7Rpc0.2应力水平蠕变数据,相比于第1组使系数C1增加了3个数量级,系数C2减小至2,得到了较大的蠕变应变计算值。第4组综合了5个应力水平的蠕变数据进行回归分析,系数C1、C2与第1组相似,计算值与试验值的误差较大。由此可见,从校正决定系数与试验值误差两个方面考虑,第2组的蠕变数据拟合结果最优。
(2)蠕变本构模型的影响
基于0.8Rpc0.2、0.85Rpc0.2、0.9Rpc0.2和1.1Rpc0.2四个应力水平的蠕变应变数据,应用Origin数据分析软件以修正的时间强化模型、时间强化模型和广义Graham模型为蠕变本构方程进行蠕变系数的非线性回归分析。
时间强化模型采用两种方法开展回归分析:第一、基于模型直接拟合;第二、分段拟合。直接拟合方法即根据本构方程对试验数据直接拟合,与上一节应力水平影响分析中修正的时间强化模型拟合方法相同。分段拟合方法是将初始蠕变阶段和稳态蠕变阶段的试验数据分开,分别以时间强化模型的第一部分和第二部分进行回归分析,最后将拟合的系数组合。
广义Graham模型具有7个蠕变系数,应用Origin数据分析软件对蠕变应变数据进行回归分析时,初始值对拟合结果影响较大,当初始值设定距离理论值偏差较大时将无法得到参数结果,校正决定系数呈现负值,拟合失败。本文以多组不同的初始值进行回归分析后,得到两组拟合结果;将两组结果应用ANSYS软件分别进行数值计算后,蠕变积分不收敛,未得到蠕变计算结果。三个模型的回归分析结果如表4所示。
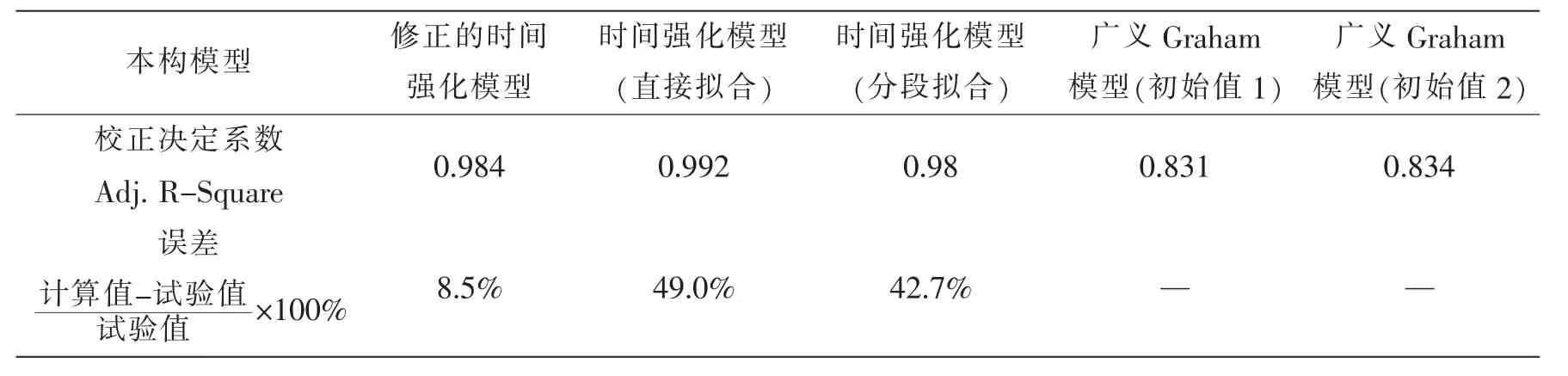
表4 不同本构模型的蠕变系数和蠕变应变Tab.4 Coefficients and strain of creep for various constitutive models
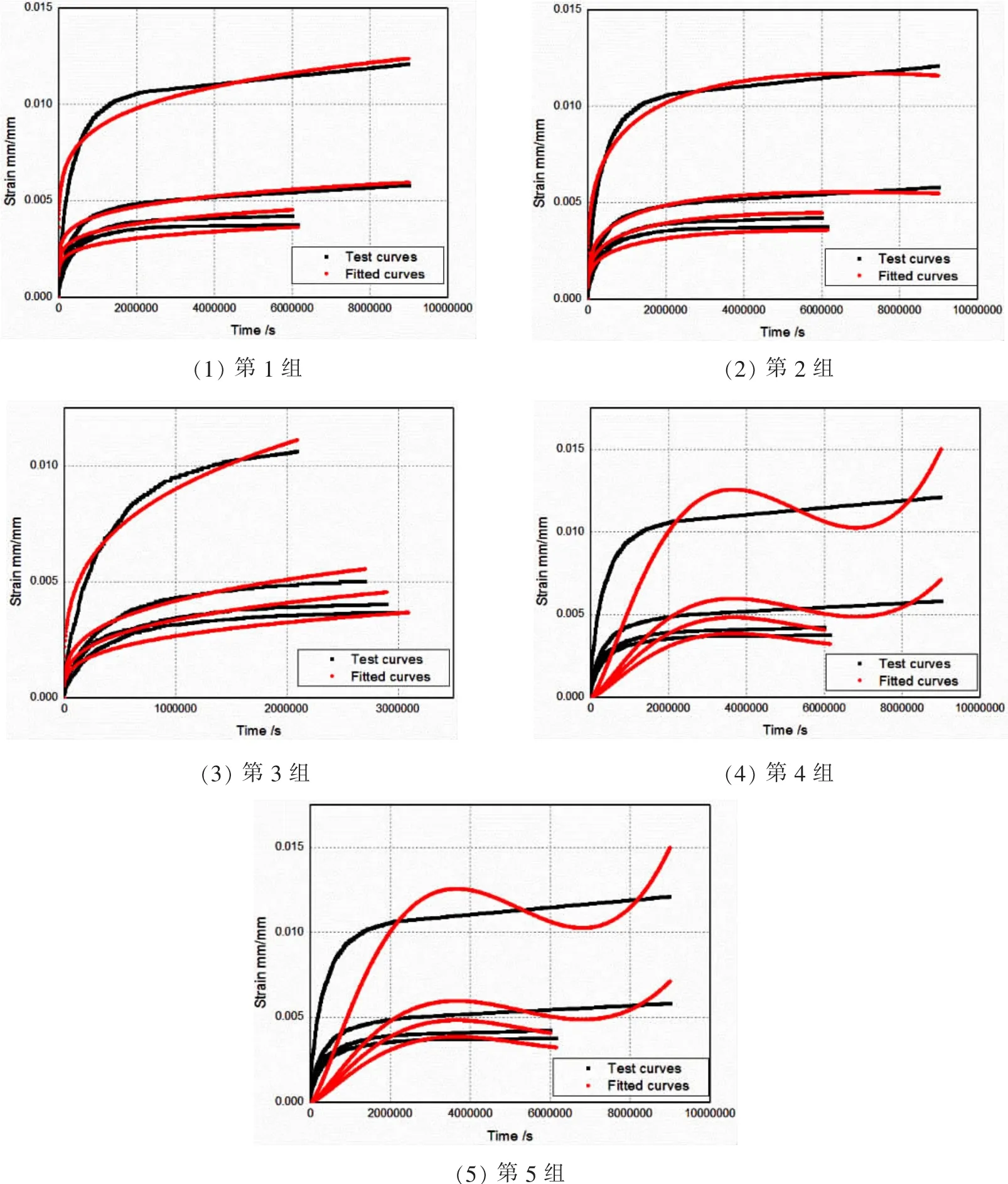
图3 不同本构模型的蠕变曲线拟合Fig.3 Fitting of creep curves for various constitutive models
由表4可知,基于修正的时间强化模型回归分析的蠕变应变计算值更接近试验值,基于时间强化模型直接拟合与分段拟合的计算结果均偏大。7个参数的Graham模型给蠕变参数回归带来了复杂的分析过程,时间项的幂指数多项式细分与系数增加虽然提升了Graham模型对蠕变应变率变化的适应性,却给蠕变积分的收敛性增加了阻碍。修正的时间强化模型蠕变系数少,收敛计算快,与试验值吻合度更好,可以较准确地表征钛合金材料的压缩蠕变特性规律。
(3)蠕变时间的影响
选取4组不同蠕变时间的蠕变数据进行拟合:第1组,全部试验数据;第2组,1 600 h的试验数据;第3组,1 300 h的试验数据;第4组,1 000 h的试验数据。应用Origin数据分析软件将上述4组数据均以修正的时间强化模型为蠕变本构方程进行蠕变系数的非线性回归分析。以拟合得到的蠕变系数作为输入,对环肋圆柱壳模型进行蠕变数值计算,并与跨中位置纵向蠕变应变的试验值进行对比,误差如表5所示。

表5 不同蠕变时间的蠕变系数和蠕变应变Tab.5 Coefficients and strain of creep for various creep time
由表5可知,选取全部试验数据进行回归分析的拟合度最高,蠕变应变计算值与试验值的误差最小,拟合结果最优。随着蠕变时间的减少,试验曲线与拟合曲线的拟合度逐渐降低;同时,计算值与试验值的误差逐渐增大。
应用1stOpt软件对0.8Rpc0.2、0.85Rpc0.2、0.9Rpc0.2和1.1Rpc0.2四个应力水平的蠕变应变数据,基于修正的时间强化模型、时间强化模型、广义Graham模型进行蠕变系数的非线性回归分析。将三种模型回归得到的蠕变系数作为材料特征输入,应用ANSYS软件分别进行数值计算,并与试验值进行对比。回归分析后计算结果如表6所示,应用1stOpt软件的蠕变参数回归分析结果与Origin数据分析软件基本相同,修正的时间强化模型计算值最优,时间强化模型的结果偏差较大,广义Graham模型的蠕变计算仍未收敛。基于钛合金压缩蠕变试验数据,1stOpt软件的非线性回归分析进一步验证了修正的时间强化模型的适用性。

表6 基于1stOpt回归的蠕变系数和蠕变应变Tab.6 Coefficients and strain of creep for different constitutive models
4 钛合金环肋圆柱壳模型的蠕变计算
建立钛合金环肋圆柱壳结构的几何模型。在此基础上,采用20节点的SOLID186单元建立有限元模型。选择映射网格依次对环肋圆柱壳、封板、加筋板等三部分结构进行网格划分,共划分为87 248个单元、487 842个节点,结构有限元模型如图5所示。

图5 环肋圆柱壳结构的有限元模型Fig.5 FEM model of ring-stiffened cylindrical shell
应用Origin数据分析软件将0.8Rpc0.2、0.85Rpc0.2、0.9Rpc0.2和1.1Rpc0.2四个应力水平的蠕变数据以修正的时间强化模型为蠕变本构方程进行蠕变系数的非线性回归分析。以拟合得到的蠕变系数作为输入,按照第1节所示的计算步骤对环肋圆柱壳模型进行蠕变数值计算。
提取蠕变模型跨中位置的等效蠕变应变,将其随时间变化情况以最大值为1的无量纲化表示,如图6所示。蠕变模型跨中位置的等效弹性应变随时间变化情况以最大值为1的无量纲化如图7所示。

图6 蠕变模型测点蠕变应变曲线Fig.6 Creep curve of creep model

图7 蠕变模型测点弹性应变变化曲线Fig.7 Elastic strain curve of creep model
提取蠕变模型跨中位置的等效应力,将其随时间变化情况以最大值为1的无量纲化表示,如图8所示。环肋圆柱壳模型蠕变前后应力和应变的极值变化情况汇总于表7。对比蠕变前后应力变化可知,模型的等效应力极值下降了14.2%,蠕变后耐压结构应力重新分配,高应力区范围有所扩大。同时,蠕变后模型的弹性应变和总应变均减小,总应变减小7.6%。
产生蠕变后环肋圆柱壳模型的最大位移变化情况如表7所示。模型总位移与纵向位移增加7.1%,位于跨中壳板处的最大径向位移增加24.4%。由此可见,相比于纵向,蠕变对环肋圆柱壳结构的径向变形影响更大。
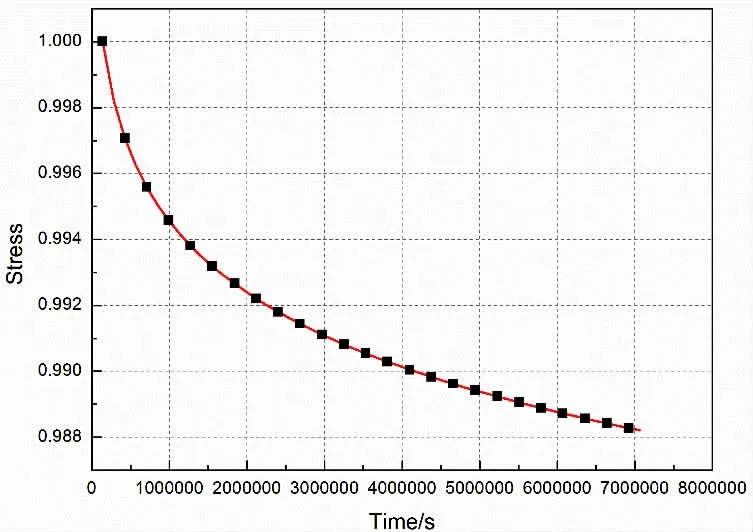
图8 蠕变模型测点等效应力变化曲线Fig.8 Equivalent stress curve of creep model

表7 模型蠕变前后的应力和应变变化Tab.7 Variations of stress and strain of creep model

表8 模型蠕变前后的最大位移变化Tab.8 Variations of the maximum displacement of creep model
5 结 论
本文对比分析多种典型蠕变本构模型,确定钛合金材料常温压缩蠕变本构方程和系数,初步建立钛合金耐压结构蠕变数值计算方法。对钛合金环肋圆柱壳模型开展蠕变计算,给出蠕变前后模型的应力、应变和位移的变化情况。本文得到以下结论:
(1)通过比较分析应力水平、本构模型、蠕变时间等三个主要影响因素,修正的时间强化模型可以表征钛合金耐压结构初始蠕变阶段和稳态阶段的蠕变特性,能够适用于深海钛合金耐压结构的蠕变计算;
(2)针对应力变化范围较大的蠕变数据非线性回归分析,基于时间强化模型的蠕变计算值与蠕变模型的试验值相比结果偏大;广义Graham模型细分的7个参数给蠕变积分计算的收敛性增加了阻碍,未形成蠕变计算结果;
(3)产生蠕变变形后钛合金耐压结构应力重新分配,高应力区范围有所扩大,蠕变后弹性应变和总应变均减小;相比于纵向,蠕变对环肋圆柱壳结构的径向变形影响更大。
