基于Hertz弹性接触的船舶推进轴系非线性校中计算
2019-03-14杨红军刘镇剑
杨红军,李 俊,刘镇剑
(上海船舶研究设计院,上海 201203)
0 引 言
大型或超大型远洋船舶多采用低速两冲程柴油机作为推进主机直接驱动螺旋桨,推进轴系承担了从主机到螺旋桨传递功率和转动的功能。螺旋桨采用类似悬臂梁的安装方式,导致尾管后轴承后端有很大的边缘载荷,不利于尾管后轴承工作。近年来,由于船舶大型化以及对航行经济性的追求,一方面,主推进功率越来越大;另一方面,推进系统采用了更低转速、更大直径的螺旋桨,螺旋桨的重量也更大。螺旋桨重量的增加使得尾管后轴承的工作条件更加恶劣,轴系对温度变化越来越敏感或船体变形导致轴承高度变化。在这种新的形势下,由于轴系设计、安装、使用不良等原因导致的尾管后轴承工作温度升高、高温报警,甚至烧损的事故案例,时有发生。
推进轴系的校中是在静止态下进行计算、安装、验证的,一个良好的静态校中可以保证轴系在运转状态下,轴承支承高度、轴承支反力、倾斜角度等指标满足相关要求,轴系可以可靠地工作。而良好的轴系安装首先建立在良好的轴系校中计算的基础上。
船舶推进轴系校中计算本质上是求解超静定连续梁,求解方法通常有三弯矩法、传递矩阵法以及有限元法。在计算过程中,一般选取轴承的中点位置作为支承点,但考虑螺旋桨的悬臂梁安装方式,我国的船标[1]推荐尾管后轴承支点距离轴承后端面1/7~1/3的轴承有效长度。
由于螺旋桨重量的增加,导致尾管后轴承的负荷增加。为了降低尾管后轴承的名义压力,需要适当增加轴承的长度。但是,在螺旋桨重量的作用下,尾轴存在一定的挠度和转角,过大的挠度和转角值使得轴系在工作过程中,轴表面和轴承表面不能很好地贴合,产生较大的局部面压,不利于尾管后轴承的润滑。因此,在通常情况下,为保证尾管后轴承和尾轴之间的贴合,尾管后轴承的中心线须倾斜安装,中国船级社规定在尾管后轴承的支点处,尾管后轴承和尾轴的相对倾角,在静态下不超过3.5×10-4rad。通常,名义许用比压被用于衡准轴承工作,但它不能很好地反映轴表面和轴承表面的贴合情况,需要引入更多的指标来指导船舶轴系校中计算,如日本船级社提出了尾管后轴承局部最大面压的要求[2]。为改善尾管后轴承的润滑,业内提出了双倾斜尾管后轴承的设计,但是传统的单支点的计算处理方法已经不能很好地给出设计方案。
国内的主机厂、船舶设计所、船厂大都引进了挪威船级社(DNV)NAUTICUS MACHINERY软件的校中模块,该模块可根据DNV规范中尾管后轴承润滑标准[3],将尾管轴承简化为两个或三个支点,根据各支点的载荷大小来设置尾管后轴承的倾斜。法国船级社提出了“ESA”弹性校中的船级符号[4],并配以其开发的Lilas弹性校中软件。该软件考虑了尾轴与尾管后轴承的弹性接触,多次应用到我国建造的高附加值船上。国内,张敏等人[5]研究了水润滑尾管后轴承多点非线性弹性支承计算模型的建立方法,将尾轴承沿长度方向分成N个分轴承,并假设每个分轴承刚度相等,为原轴承的1/N。然而,每个分轴承的支承刚度却和载荷以及实际接触情况有关,并不相等,但是,这种假设简化了计算。
船舶推进轴系中,尾管后轴承和尾轴的接触计算具有边界非线性特点,主要是由于尾管后轴承是长轴承,接触范围取决于螺旋桨重量、桨轴直径、轴承和螺旋桨的相对位置以及轴承的倾斜情况,事先是未知的,因此需要在计算过程中进行判断、搜寻。使用平面梁单元对第二代四十万吨矿砂船推进轴系进行建模,建立轴系校中有限元模型;同时将尾管后轴承等分成多个轴承段,使用Hertz接触理论对各个轴承段进行受力分析,计算接触位移、接触力和接触刚度等参数;对有限元模型和轴承段的接触模型进行迭代求解,得到尾管后轴承和尾轴的接触情况。
1 船舶推进轴系的有限元模型
1.1 梁单元的刚度矩阵
在结构力学中,通常将承受横向力和弯矩的杆件称为梁。假设不考虑梁的剪切应变,可以用欧拉—伯努利梁假设,即忽略剪切应变,假设变形前垂直梁中心线的截面,变形后仍然为平面,且仍然垂直中心线。如图1所示的平面欧拉—伯努利梁单元,其结点为i和j上所受横向力和弯矩,分别是Fi、Mi和 Fj、Mj,对应结点位移为 νi、θi和 νj、θj。
根据有限元方法的基本原理,单元的位移模式具备完整性和协调性,因此单元的横向位移和转角是连续的。可将单元的结点位移表示成一定的多项式形式,就可以进行单元的力学特性分析,得到作用在单元上结点力和结点位移之间的关系,并根据最小势能原理,求得单元的刚度矩阵,如下式所示:
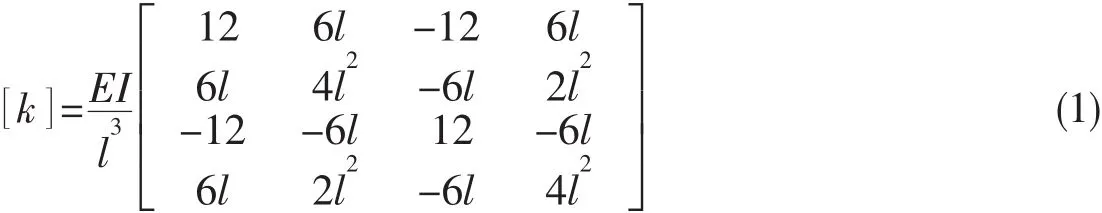
式中:E是材料的弹性模量,I是截面惯性矩,l为单元长度。
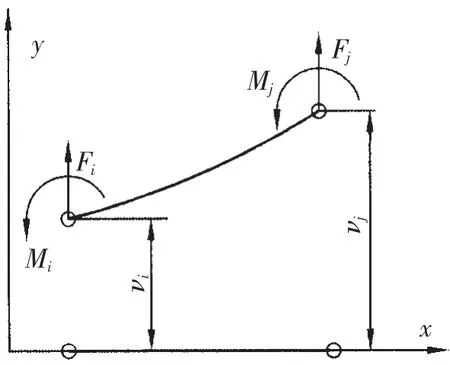
图1 平面梁单元Fig.1 Model for plane beam element
在推导梁单元刚度矩阵和计算等效结点载荷时,采用的是局部坐标系,将单元的刚度矩阵和等效结点力转移到实际结构坐标系的对应值后,就可以进行总刚度矩阵和节点力向量的组装。最后得到了整个结构的平衡方程

式中:K为总刚度矩阵,δ为节点位移向量,f为节点力向量。
1.2 边界条件的处理
由于整体刚度矩阵在组装时,没有考虑整体结构的平衡条件,所以得到的整体刚度矩阵是一个奇异矩阵,只有在引入边界约束条件后,对所建立的平衡方程(2)做适当修改,才能根据方程组的具体特点,选择适当的计算方法求得节点位移。继而求出单元的应变和应力。值得注意的是,引入边界条件,修改平衡方程,实质上就是消除结构的刚体位移。
对于位移约束条件可以使用划行列的方法。但对于如图2所示的弹性支承,假设沿着梁第i自由度有位移约束ai,且弹性支承的刚度为Ci,根据最小势能原理,只需对总刚度矩阵中对应自由度的对角元素和节点力载荷向量中对应自由度的元素进行修改[6],如下式所示:

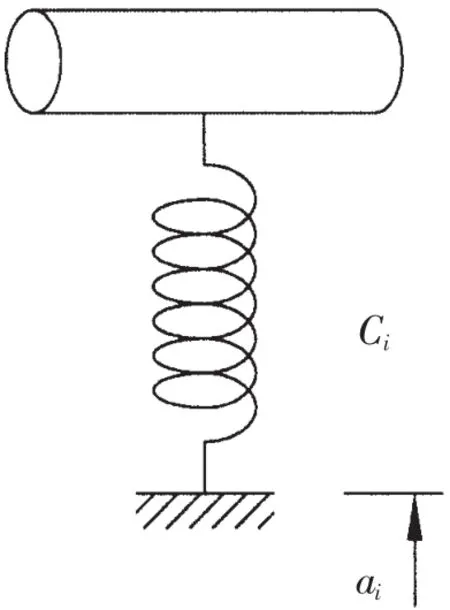
图2 弹性支承示意Fig.2 Sketch for elastic support
2 轴和轴承的接触模型
Hertz接触理论是根据完全弹性体的静态接触条件提出的,可用来计算曲面接触副的弹性变形和应力场。Hertz接触模型基于如下的假定:①接触区域为均匀材料,发生接触时未超过屈服应力;②接触应力沿着接触切平面的法线,即接触体之间不存在切向力;③接触面积要小于接触体的尺寸;④接触体处于自由平衡状态;⑤不考虑接触面的粗糙度。如图3所示的两圆柱的圆心在接触点同一侧,RA和RB分别为两圆柱的半径,且RA<RB,2×len为圆柱长。两相同长度的弹性圆柱在载荷W作用下,发生挤压,接触线扩展成一个狭长的面,其半宽为b。则接触半宽,最大面压和接触变形可由以下公式进行计算[7]。

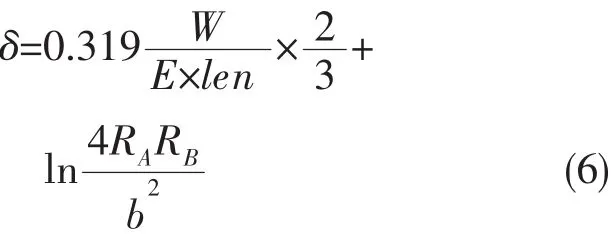
在传统的船舶推进轴系校中计算中,通常将尾管后轴承,简化为一个支点,用轴承的名义比压以及支点处尾管后轴承与螺旋桨轴的相对倾角来衡准计算结果。由于尾轴自身存在挠度变形,轴的中心和轴承中心并不平行,轴和轴承之间存在很大的边缘载荷,部分区域的轴承压力较大。为了对尾管后轴承的实际工作进行更好的模拟,我们把尾管后轴承分成多段,如图4所示。这样可以很好地模拟轴表面和轴承表面之间的帖合情况。
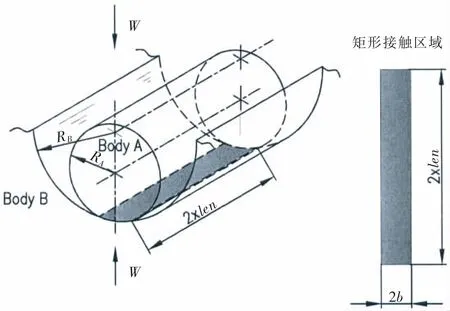
图3 两平行弹性圆柱的接触模型Fig.3 Contact model between two parallel elastic cylinders
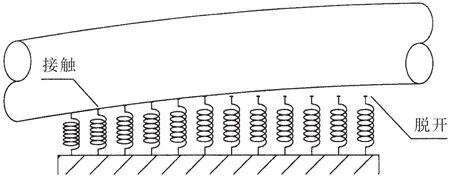
图4 尾管后轴承多段支承示意Fig.4 Multi-support for after stern tube bearing
在计算过程中,首先根据尾管后轴承分支点初始位移判断轴承段和相应轴段是否存在接触,使用Hertz接触模型求解接触力和接触刚度,然后求解有限元模型,判断结果是否收敛,如果不收敛就调整支点高度,进行下一步计算,具体流程如图5所示。
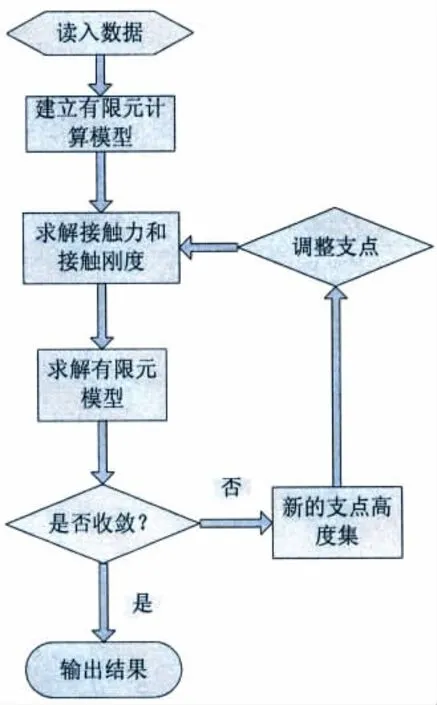
图5 计算流程图Fig.5 Flow chart for calculation
3 算 例
3.1 计算模型
第二代四十万吨矿砂船,使用7S80MEC9主机,直接驱动螺旋桨,其推进轴系校中计算模型如图6所示。尾管后轴承后端面定位于2 927 mm,前端面定位于4 737 mm,尾管前轴承使用单支点弹性支承模型,具体定位是9 057 mm处。
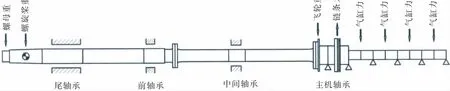
图6 轴系校中计算模型Fig.6 Model for shaft alignment calculation
3.2 计算结果与分析
首先对尾管后轴承单支点模型进行了计算,并假定尾管后轴承支点距尾管后轴承的后端面的距离为四分之一的轴承有效长度,各轴承负荷如表1的第1行所示,尾管后轴承支点处的转角为0.53 mrad,根据该转角值,我们采用尾管后轴承中心0.4 mrad和0.53 mrad的单倾斜方案,以及0.55/0.4 mrad和0.7/0.5 mrad的双倾斜方案进行计算。双倾斜的斜率转折点在尾管后轴承的中点处。图7为0.55/0.4 mrad双倾斜轴承示意,L为总长,轴瓦后半段与水平线的夹角是0.55 mrad,轴瓦前半段与水平线的夹角是0.4 mrad。轴承负荷如表1所示。在轴系支点高度相同的情况下,不同的尾管后轴承的倾斜设定只影响尾管前后轴承的负荷,中间轴承和主机轴承影响较小。将尾管后轴承分成20等份,使用Hertz接触理论计算每一段轴承和轴的接触力学特性。尾管后轴承与轴的接触范围如图8~11所示。
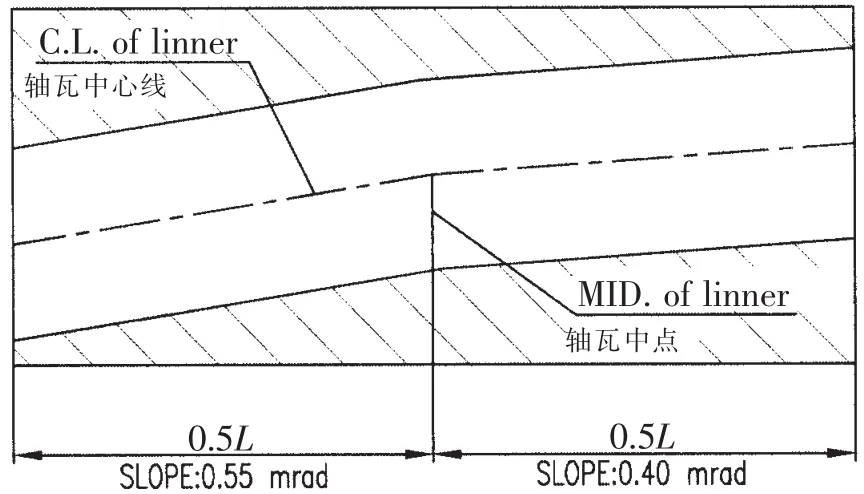
图7 0.55/0.4 mrad双倾斜示意Fig.7 Sketch for SLOPE 0.55/0.4 mrad
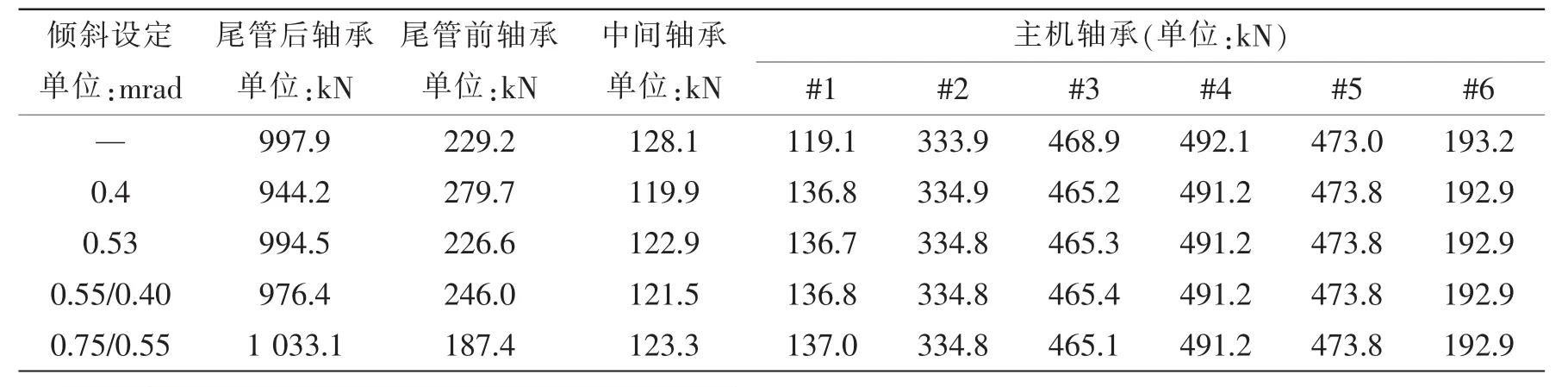
表1 各计算工况下轴承负荷Tab.1 Bearing loads for each calculation condition
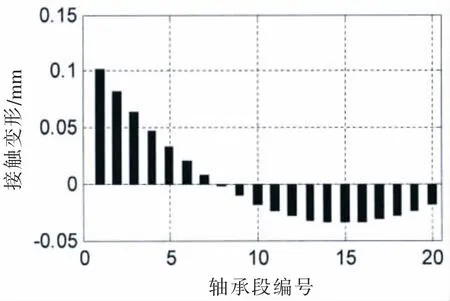
图8 (a) 接触变形@SLOPE 0.4 mradFig.8(a)Contact deformation@SLOPE 0.4 mrad
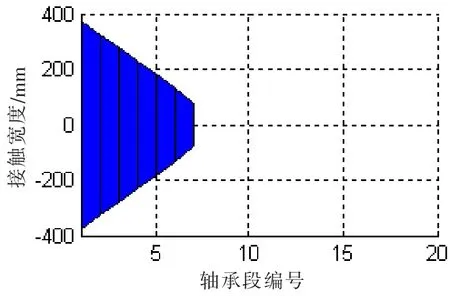
图8 (b)接触宽度@SLOPE 0.4 mradFig.8(b)Contact width@SLOPE 0.4 mard
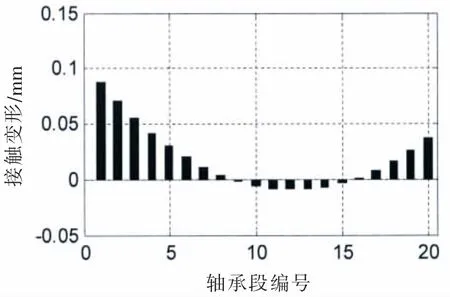
图9 (a) 接触变形@SLOPE 0.53mrad Fig.9(a)Contact deformation@SLOPE 0.53mrad
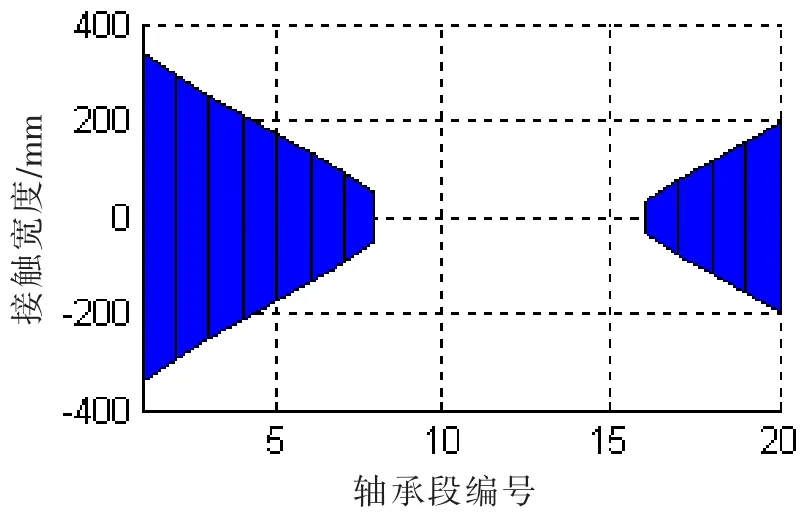
图9 (b)接触宽度@SLOPE 0.53mradFig.9(b)Contact width@SLOPE 0.53mard
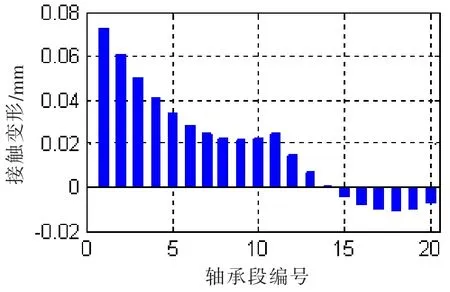
图10 (a) 接触变形@SLOPE 0.55/0.4 mradFig.10(a)Contact deformation@SLOPE 0.55/0.4mrad
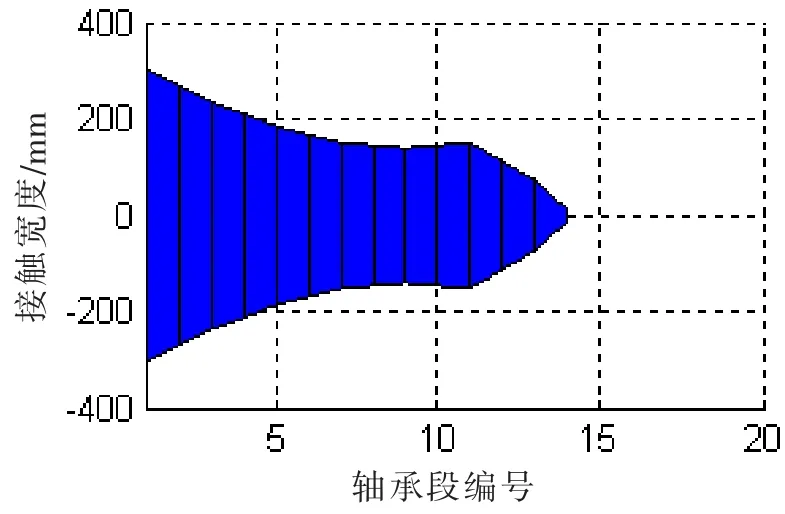
图10 (b)接触宽度@SLOPE0.55/0.4 mradFig.10(b)Contact width@SLOPE 0.55/0.4mard
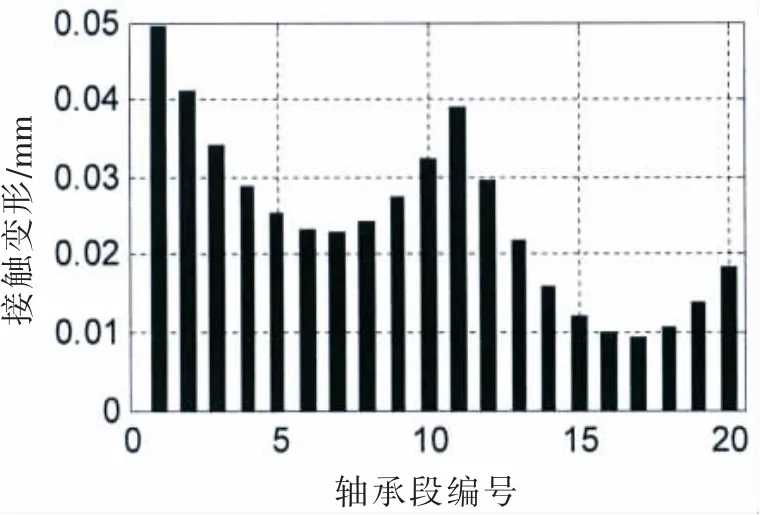
图11 (a) 接触变形@SLOPE 0.7/0.5 mradFig.11(a)Contact deformation@SLOPE 0.7/0.5 mrad
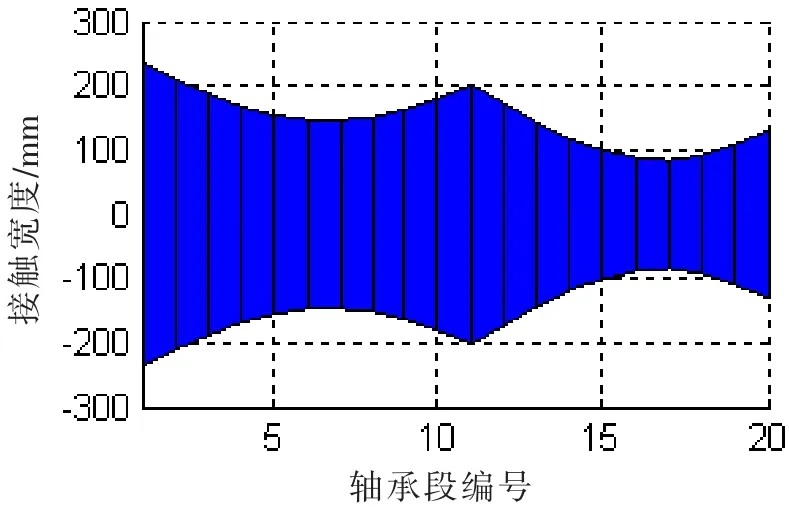
图11 (b)接触宽度@SLOPE0.7/0.5 mradFig.11(b)Contact width@SLOPE 0.7/0.5 mard
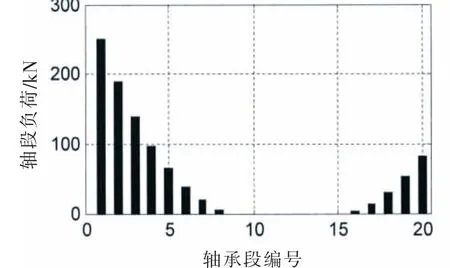
图12 (a)轴承段负荷@SLOPE 0.53 mradFig.12(a)Bearing load@SLOPE 0.53 mrad
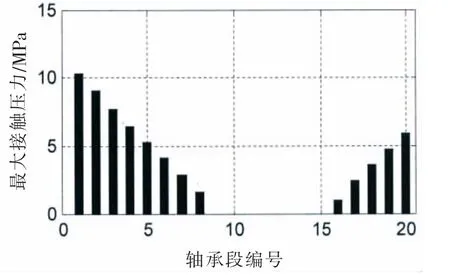
图12 (b)接触刚度@SLOPE 0.53 mradFig.12(b)Contact stiffness@SLOPE 0.53 mard
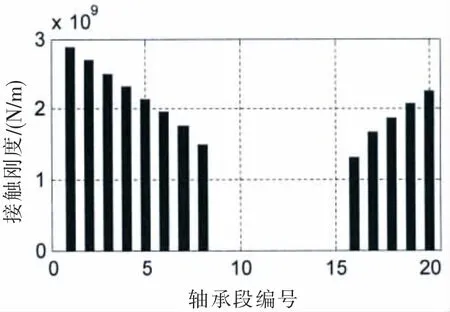
图12 (c)最大接触压力@SLOPE 0.53 mradFig.12(c)Max contact pressure@SLOPE 0.53 mard
在接触变形图中,X轴以上柱状图高度为正,表征接触变形量δ,X轴以下的柱状图高度为负,表征轴和轴承之间的间隙。在不同的尾管后轴承中心倾斜条件下,接触变形和接触区域是不同的。各个轴承段的最大接触变形小于0.1 mm,而尾管轴承的白合金厚度为3 mm;只有在0.7/0.5 mrad的双倾斜状态下,轴和轴承在长度方向是完全接触的。更大的接触范围,可以获得较小的接触压力,在轴系运转时,更容易形成油膜,延长尾管后轴承的工作寿命。在计算得到接触变形和接触范围后,可以方便地得到Hertz接触力,即轴承段的负荷,以及最大接触压力和接触刚度。以0.53 mard的单倾斜和0.55/0.4 mrad双倾斜为例,其计算结果如图12和13所示。
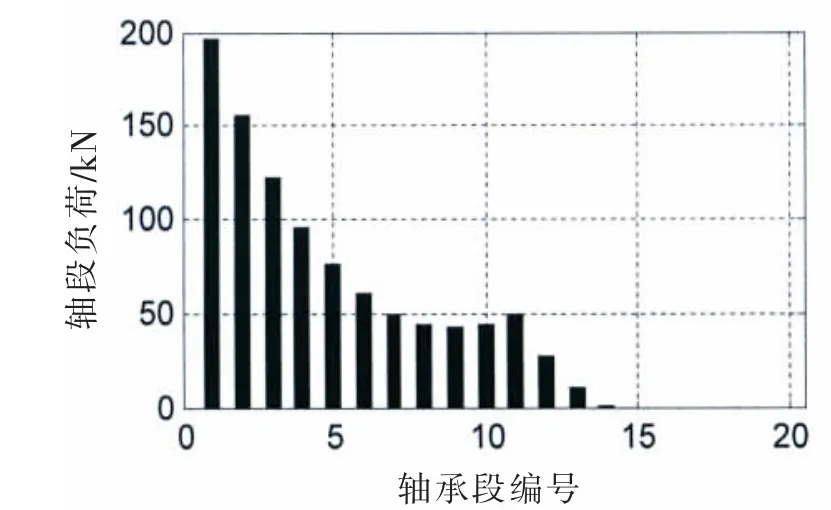
图13 (a)轴承段负荷@SLOPE 0.55/0.4 mradFig.13(a)Bearing load@SLOPE 0.55/0.4 mrad
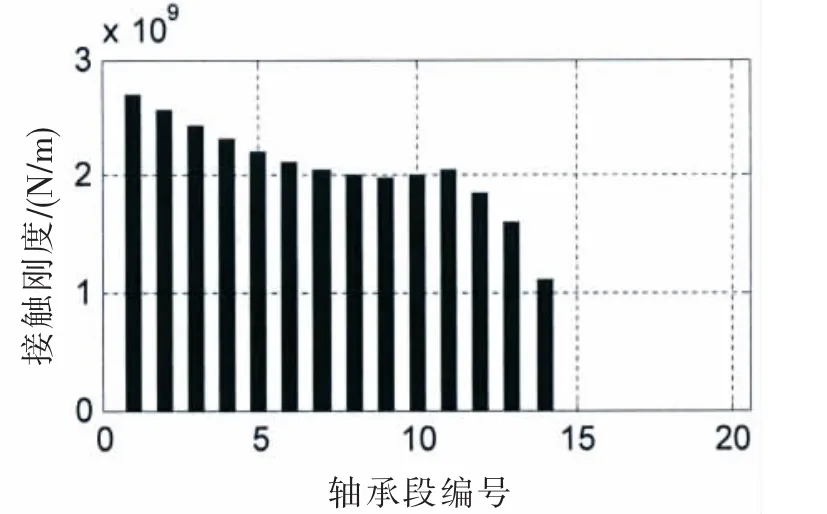
图13 (b)接触刚度@SLOPE 0.55/0.4 mradFig.13(b)Contact stiffness@SLOPE 0.55/0.4 mard
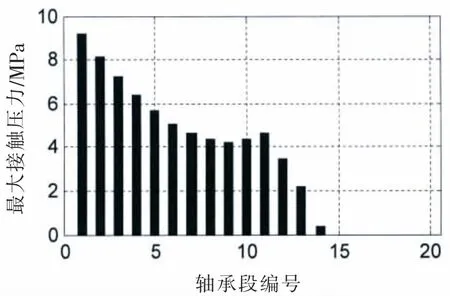
图13 (c)最大接触压力@SLOPE 0.55/0.4 mradFig.13(c)Max contact pressure@SLOPE 0.55/0.4 mard
对比图12和图9,图13和图10,轴承段负荷的柱状图和接触变量的柱状图的形状是比较一致的,轴承段负荷和接触变形量基本呈正相关。接触刚度的柱状图高度相对较均匀,接触刚度在109N/m量级,和文献[8]内容基本一致。由计算结果可知,四种计算工况,结合表一中的尾管后轴承负荷,在较小的尾管后轴承倾斜设定下,轴承和轴的接触区域主要在轴承的后边缘或者后半部分;在较大的单倾斜设定下,在轴承的前后端轴承和轴都有接触,因此大倾斜设定的尾管后轴承的等效支点相对靠前一些,导致尾管后轴承负荷增加。
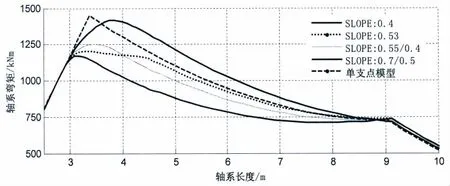
图14 尾管前后轴承之间的轴系弯矩图Fig.14 Moment curve between after and forward s/tube bearing
图14为尾管前后轴承之间的弯矩图,由于螺旋桨最末端、中间轴以及曲轴上的弯矩计算结果基本相同,图中仅仅显示了尾管前后轴承之间轴系上的弯矩。对于尾管后轴承的单支点模型计算结果,由于尾管后轴承支反力很大,使得在支点处剪力改变了符号,因此,支点处的弯矩存在转折点。但对于尾管后轴承多点支承的非线性模型,支点是通过实际的轴承中心倾斜情况计算搜索得到的,且是多个分支点共同起作用,分支点的支反力逐渐使剪力改变符号,弯矩曲线开始下降,因此尾管后轴承处弯矩曲线是近似圆弧过度;对于较小的尾管后轴承倾斜,轴承和轴的接触位于后端,弯矩的峰值较低,而较大的尾管后轴承倾斜,使得弯矩峰值较高,较前者升高将近20%,也使得螺旋桨轴上的弯曲应力也升高将近20%,影响很大。如中国船级社规定螺旋桨轴上的最大弯曲应力不得超过20 MPa。由于轴承倾斜设置不同,轴系挠度曲线也有差别,图15为轴系末端到尾管后轴承的挠度曲线,0.4 mrad的SLOPE挠度最小,0.7/0.5 mrad挠度最大。
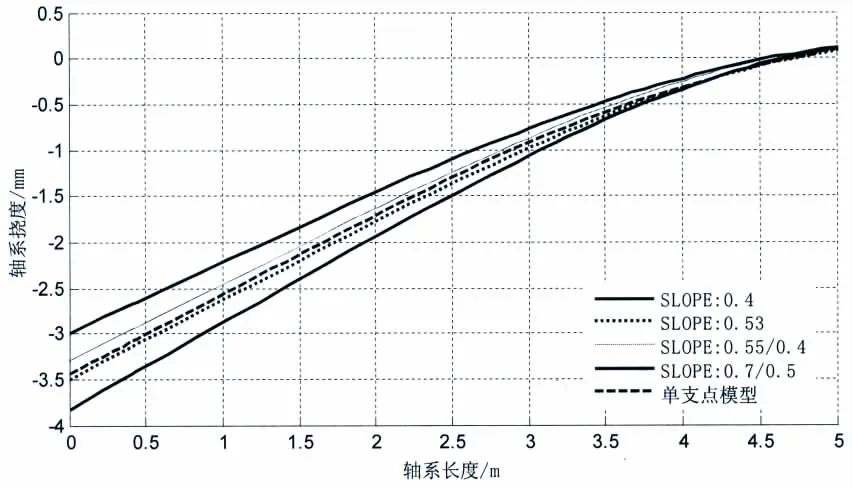
图15 轴系末端到尾管后轴承的挠度曲线Fig.15 Deflection curve from end of shaft to after s/tube bearing
4 结 论
(1)将尾管后轴承等分成多个轴承段,用Hertz弹性接触模型描述轴承和轴的接触力学特性,结合平面梁单元的轴系校中计算有限元模型,可以获得尾管后轴承和轴的接触范围、接触变形、接触最大面压、接触刚度等计算结果。这些是尾管后轴承单支点计算模型无法达到的。
(2)根据轴承段的最大接触压力以及轴承段负荷等结果,可以更好地设置尾管后轴承的倾斜。保证轴系运转时尾管后轴承和轴有较好的贴合,同时可以防止轴和轴承之间过大的接触压力,以及在轴系启动运转时可能会导致白合金的擦伤或者剥落。
(3)尾管后轴承的支点位置不用在计算前假定,而是由多个分支点承担。根据实际的轴承中心倾斜情况,由计算结果轴段负荷的分布情况来确定。且轴承的支承刚度也可以根据计算结果确定,不需事先假定。
