控制杆对柔性圆柱涡激振动的抑制效果研究

徐万海 ， 杨 猛 ，， 芦 燕

（1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2.天津大学 建筑工程学院，天津300072）

0 引 言

涡激振动（Vortex-induced vibration，VIV）是引起海洋立管、海上浮式风机系泊缆等大长径比柔性圆柱结构疲劳损伤的重要因素。如何抑制VIV是工程界与学术界长期关注的焦点问题。涡激振动的抑制方式主要有两种，即主动控制和被动抑制。主动控制通过监测流场和结构受力，运用计算机自动控制技术，引入适当的扰动改变流场。但其操作复杂，成本较高，技术难度大，工程实际中的应用受到较大限制。被动抑制直接改变结构表面形状或安装附加装置，改变结构周围的流场，这种方式在实际工程中的应用十分广泛[1-6]。

根据机理的不同，被动抑制装置可分为3类：（1）表面突出结构，如螺旋列板（helical strakes）、突起（bumps）等；（2）尾流控制装置，如整流罩（fairings）、分隔板（splitter plate）等；（3）覆盖结构，如轴向板条（axial rod shroud）、控制杆（control rod）等[7]。 上述VIV抑制装置各有优劣。 Vandiver等[8]开展了现场实验，观测了螺旋列板的VIV抑制效果，发现螺旋列板在减小高阶模态振动幅值的同时还能降低三次谐波成分，但同时也增大了结构顺流向受到的拖曳力。Allen[9]通过模型实验观测发现：整流罩对于涡激振动和拖曳力的抑制效果明显，但流速过大时，立管将发生很大的横向振动，存在动态不稳定性。Akilli等[10]实验发现分隔板对VIV具有较好的抑制效果，但只对单个来流方向起作用。Tsutsui和Igarashi[11]在实验中发现单根控制杆能够降低主管的脉动升力和拖曳力，并优化了控制杆的直径d=0.25D（D为主管直径），但单根控制杆仅对某些来流方向效果明显。宋吉宁等[12]的实验研究表明：三根控制杆抑制装置对来流方向适应性很强。Wu等[13]开展附有四根控制杆的海洋立管涡激振动实验，研究了覆盖率和间距（控制杆外表面到立管模型外表面的距离）对抑制效果的影响，表明覆盖率越高，间距越小，抑制效果越好。

1 实验方案

实验观测在天津大学水利工程仿真与安全国家重点实验室的拖曳水池中完成，水池长137.0 m，宽7.0 m，深3.3 m。开展了三组实验：（1）柔性圆柱模型涡激振动实验；（2）附有三根控制杆抑制装置的柔性圆柱模型涡激振动实验；（3）附有四根控制杆抑制装置的柔性圆柱模型涡激振动实验。三组实验中的柔性圆柱模型两端通过万向节固定在拖车底部的刚架上，两端施加的预张力均为450 N。三组实验分别进行，使用相同的柔性圆柱模型。拖曳水池上方的拖车拖动模型匀速前进，可模拟均匀来流条件，待圆柱振动达到稳定状态时，开始数据采集，采样频率100 Hz，采集时间50 s。实验中拖车的速度范围为0.05～1.00 m/s，间隔为 0.05 m/s，共计测量 60个实验工况，实验中雷诺数最大可达到16 000。

图1 实验模型Fig.1 Experimental models

柔性圆柱模型的内芯为铜管，沿轴向均匀设置七个测点，每个测点的横流向和顺流向布置应变片，用于采集振动信息。模型外层为硅胶管，以保证外表面光滑，并防水绝缘。控制杆模型采用外径为0.25D的圆形截面塑胶条，间距为0.5D，固定在塑料材质的支撑装置上。支撑装置有两种，分别可以等间距地固定三根控制杆和四根控制杆。图1为上述三组实验中的模型。控制杆与柔性圆柱模型的排布方式如图2所示。制作控制杆和支撑装置的材料在水中的比重近似等于1，对柔性圆柱模型整体质量比的影响很小。详细的圆柱模型结构参数如表1所示。

表1 光滑圆柱模型参数Tab.1 Physical property for the cylinder model

图2 控制杆与圆柱模型的布置图Fig.2 Sketch of cylinder model with control rods

采用模态法处理采集得到的应变信息。模态法可以通过柔性圆柱上若干个离散点的应变信息获得整个结构上任一点的位移信息[14-15]，以横流向为例介绍模态法。

建立如下坐标系：x轴对应顺流向，y轴对应横流向，z轴对应柔性圆柱模型轴向。对于长度为L的柔性圆柱振动问题，其横流向振动位移用模态叠加的方法可以表示为：

其中：y（ z,t）为柔性圆柱横流向振动位移，Wn（t）为权重函数，φn（z）为模态函数，n为柔性圆柱振动模态阶次。本实验中柔性圆柱模型两端均为简支边界条件，因此模态函数φn（z）可表示为：

若在柔性圆柱模型上布置M个应变片，其振动位移可以采用N阶模态的线性叠加来表示，则横流向的曲率矩阵Py可以用下式表达：

其中：

其中：ε（ z,t）为测量的应变信号，R为内芯铜管半径。实验中，柔性圆柱模型横方向激发的最高阶模态为4，即N=4，应变片的布置数M=7，所以N＜M，权重函数可以采用最小二乘法来求得：

图4(a)、(b)分别为改进型ADRC和双闭环PID对小车位置的控制曲线，图4(c)、(d)分别是改进型ADRC和双闭环PID对小车位置的控制曲线。通过对比可以看出改进型ADRC在2s以后就可以稳定控制摆杆角度和小车位置，而双闭环PID在3s以后失去对摆杆和小车位置的控制；通过仿真可以看出基于改进型的ADRC的一级直线倒立摆系统具有较好的鲁棒性。

将（7）式代入（1）式即可求出柔性圆柱模型的横流向振动位移。顺流向的振动位移确定方式与横流向类似，在此不再赘述。

2 抑制效果分析

控制频率是反映柔性圆柱涡激振动特性的重要信息。图3和图4给出了三组实验中圆柱模型涡激振动横流向（CF）和顺流向（IL）的控制频率随流速变化情况。可以看出，三种模型的控制频率均随流速线性增加。附有控制杆的圆柱模型控制频率显著低于不带控制杆的光滑圆柱，四根控制杆的控制频率比三根控制杆低，顺流向尤为显著。对比图3和图4可发现，光滑圆柱和附有三根控制杆的抑制圆柱顺流向控制频率大约为横流向的2倍，而附有四根控制杆的抑制圆柱顺流向和横流向的控制频率几乎一致。当流速为0.95 m/s和1.0 m/s时，三根控制杆圆柱模型的横流向涡激振动控制频率出现了突然下降，产生该现象的原因为控制模态由高阶转化为低阶，导致了主控频率的降低。总而言之，多根控制杆能降低圆柱模型的控制频率，四根控制杆的效果优于三根控制杆，前者能极大地降低结构顺流向的控制频率。

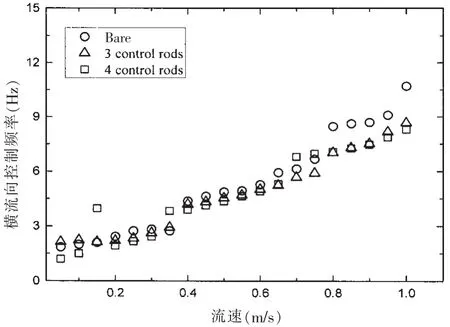
图3 横流向控制频率随来流速度变化Fig.3 CF dominate frequency versus flow velocity

图4 顺流向控制频率随来流速度变化Fig.4 IL dominate frequency versus flow velocity

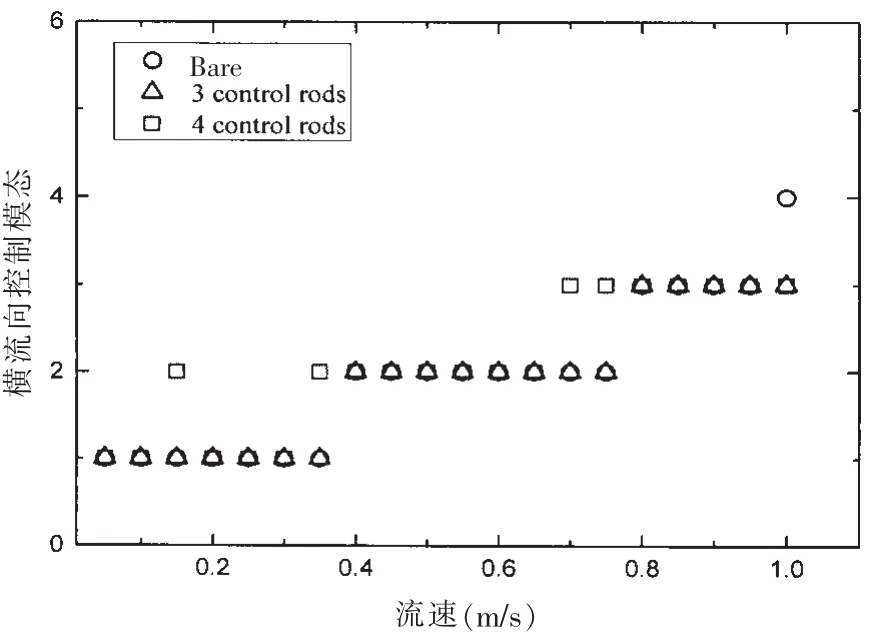
图5 横流向控制模态随来流速度变化Fig.5 CF dominate mode versus flow velocity

图6 顺流向控制模态随来流速度变化Fig.6 IL dominate mode versus flow velocity

柔性圆柱模型涡激振动特性的另一重要参数是控制模态。图5和图6反映了三种实验模型涡激振动的控制模态。从图中可以看出，所有模型横流向和顺流向最低控制模态均为1阶。光滑圆柱横流向和顺流向的最高控制模态分别为4阶和6阶，附有三根控制杆的模型为3阶和4阶，而附有四根控制杆模型横流向与顺流向均为3阶。可见控制杆能降低圆柱模型涡激振动激发的最高模数，对顺流向的抑制效果更加显著，四根控制杆对控制模态的抑制效果略优于三根控制杆。

应变是实验中直接测量得到的信号，与结构受到的应力直接相关，是反映结构涡激振动疲劳破坏的重要指标。图7和图8为三组实验中圆柱模型的最大应变均方根值。图9和图10给出了来流速度为0.5 m/s时，圆柱模型测点处的应变时间历程曲线和对应的频谱分析图。可以看出，控制杆显著减小了圆柱模型涡激振动的应变，对顺流向的抑制效果更为明显，四根控制杆的作用效果比三根控制杆略好。从频谱图中可以看出，光滑圆柱的应变响应频率最高，三根控制杆和四根控制杆响应频率差异不明显，三根控制杆略高。光滑圆柱的应变响应频率出现了幅值较高的高频成分，控制杆能降低圆柱模型的应变响应频率，并抑制高频成分的幅值。

图7 横流向最大应变均方根随来流速度变化Fig.7 Max RMS CF strain versus flow velocity

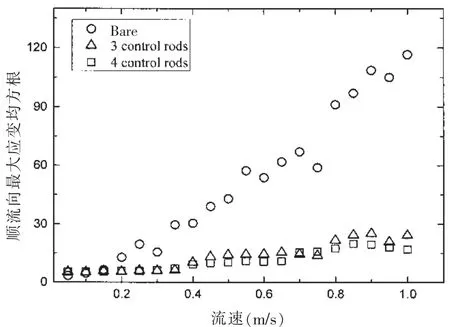
图8 顺流向最大应变均方根随来流速度变化Fig.8 Max RMS IL strain versus flow velocity

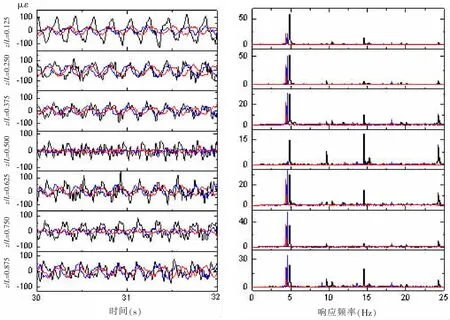
图9 测点处横流向应变时间历程曲线和频谱分析结果（黑色为光滑圆柱，蓝色为三根控制杆，红色为四根控制杆，V=0.5 m/s）Fig.9 CF strain history and its spectra at measured positions(Black for bare,blue for 3 control rods,red for 4 control rods,V=0.5 m/s)

图10 测点处顺流向应变时间历程曲线和频谱分析结果（黑色为光滑圆柱，蓝色为三根控制杆，红色为四根控制杆，V=0.5 m/s）Fig.10 IL strain history and its spectra at measured positions(Black for bare,blue for three control rods,red for four control rods,V=0.5 m/s)

图11和图12为三组实验中模型的最大位移均方根。图13和图14为来流速度为0.5m/s时，圆柱模型测点处的位移时间历程曲线和对应的频谱分析图。在流速低于0.35 m/s时，附有控制杆的圆柱模型顺流向响应位移比高流速范围时显著增大，这是不合理的，其原因在于模型的响应位移是通过模态法求得的，低阶模态振动对应的应变信号非常小，对测量噪声比较敏感，模态法很难辨别低阶模态响应的真实信号和噪声误差，来流速度较低时测量噪声会将较大的误差引入位移计算中，圆柱模型安装控制杆后，低流速下的噪声干扰比光滑圆柱时更加明显[16]。基于上述分析，可以认为来流速度低于0.35 m/s时，附有多根控制杆圆柱模型的计算位移主要是由噪声误差造成的，在分析其位移时仅考虑流速大于0.35 m/s的结果。

可以看出，控制杆能显著减小柔性圆柱模型的响应幅值，四根控制杆的响应幅值比三根控制杆小。从频率分析图中可以看出，光滑圆柱的位移响应频率最高，四根控制杆最低，三根控制杆位于两者之间。光滑圆柱的位移响应频率出现了高频成分，而控制杆对高频成分有抑制效果。

图14 测点处顺流向位移时间历程曲线和频谱分析结果（黑色为光滑圆柱，蓝色为三根控制杆，红色为四根控制杆，V=0.5 m/s）Fig.14 IL displacement history and its spectra at measured positions(Black for bare,blue for three control rods,red for four control rods,V=0.5 m/s)

3 结 论

本文开展了三组高雷诺数条件下柔性圆柱模型涡激振动实验，对柔性圆柱模型、附有三根控制杆和四根控制杆的圆柱模型的涡激振动特性进行了观测，通过对控制频率、控制模态、结构应变、响应位移等方面对比分析，分析了控制杆对柔性圆柱涡激振动的抑制效果，得到了如下结论：

（1）控制杆对柔性圆柱涡激振动抑制效果明显，对顺流向的抑制作用更加突出；

（2）总体而言，四根控制杆的抑制效果优于三根控制杆；

（3）控制杆能抑制柔性圆柱涡激振动响应频率的高频成分。

实际工程中，海洋立管的周围会部署若干管径和刚度相对于立管均很小的附属管，如在设计时合理确定附属管与立管的空间位置就相当于安装控制杆并优化其排布。排布合理的多根控制杆对流向适应性强，对抑制大长径比柔性圆柱涡激振动具有很广阔的前景。因此，有待进一步深入研究控制杆的空间排布对柔性圆柱VIV抑制的影响规律。