船舶横摇混沌阈值的数值方法研究

刘亚冲

（中国船舶及海洋工程设计研究院 基础研究部，上海200011）

0 引 言

迄今，梅尔尼科夫方法是研究确定性动力系统全局稳定性的唯一解析方法。它通过构造系统的梅尔尼科夫函数，求解该函数的一阶简单零点得到系统Poincare映射具有Smale马蹄变换意义下混沌阈值，作为检测混沌阈值的解析方法已被成功应用于许多系统中[1-3]。一般情况下，解析求解梅尔尼科夫函数时，需要先求出系统的同宿或异宿轨道的参数表达式，然后将其代入到梅尔尼科夫函数中，再利用积分表或留数定理计算。但直接对轨道方程进行解析求解较为困难。针对这一问题，本文选取两种数值方法对达芬振子系统求解梅尔尼科夫函数，并对两种数值方法进行对比分析。一种是用函数逼近的方法得到轨道方程的近似表达式，而该近似表达式易于进行积分计算；另一种是通过对相函数分析，将梅尔尼科夫函数的积分转化到易于进行的积分域上进行。

梅尔尼科夫函数有简单零点只是系统出现混沌运动的必要条件，因此在计算出混沌阈值后还应该进行数值验证。庞加莱映射、安全池和李雅普诺夫指数是三种常用的混沌识别方法，本文选取李雅普诺夫指数谱对谐和激励作用下的达芬系统进行数值验证。

运动的有界性问题通常采用“安全盆”的概念来描述，它被定义为所有有界解吸引域的集合，其中安全盆侵蚀现象通常用来解释动力系统的全局失稳行为。这一概念最早由Thompson[4]等在研究船舶的倾覆问题时提出，并被应用到不同的工程领域中。对于船舶运动系统而言，安全池是满足船舶横摇角和横摇角速度的稳态解落在一有界域的所有初值的集合，稳态解一旦超出这个有界域，船舶就无法提供足够大的复原力矩来抵抗倾覆力矩，从而发生倾覆。在本文最后，采用梅尔尼科夫方法对某型船的横摇混沌阈值进行了计算，并观察了安全盆从完整到侵蚀的过程。

1 非线性动力系统的梅尔尼科夫函数

杜芬振子作为一类非线性动力系统，具有广泛的应用背景。典型的杜芬振子的表达式为：

其中：α为阻尼系数，β和γ为恢复力系数，ζ为激振力幅值。

令 β=-1，γ=1，α=εα1，ζ=εζ1；α,ζ=o（ε）。 将上式写成状态向量正则方程的形式为：

当 α1=ζ1=0 时，（2）式退化到无扰系统（3），其 Hamilton 量和势函数分别为（4）式和（5）式。

无扰系统（3）的平衡点为 s（0,0）、cl（-1,0）和cr（1,0），其中s为鞍点，cl和cr为左右中心。当H（0,0）时，存在两条连接鞍点的同宿轨道。过鞍点的同宿轨道满足方程

同宿轨道有左右对称的两支，t∈（-∞,+∞）时，轨线从鞍点出发绕中心点顺时针旋转一周，最终再回到鞍点，同宿轨道和势函数见图1。由图不难看出，x（t）为偶函数，y（t）为奇函数。

图1 无扰系统的同宿轨道和势函数图Fig.1 Homoclinic orbit and potential function of undisturbed system

当 α≠0，ζ≠0，且足够小时，（2）式仍为可积系统。按照Smale-Birkhoff同宿理论[5]，同宿轨道的稳定流形与不稳定流形横截相交可能使非线性动力系统出现混沌。

设无扰系统同宿轨道的参数方程为xi（t）和 yi（t），受扰系统（2）同宿轨道的梅尔尼科夫函数可写为：

其中：

根据梅尔尼科夫理论，若M（ t0）具有不依赖ε的简单零点，即存在M（ t0）=0且，则对于充分小的ε，Poincare映射具有Smale马蹄变换意义下的混沌。因此，出现同宿轨线横截相交的必要条件是

2 梅尔尼科夫函数零点的数值算法

2.1 类帕德逼近方法

对于较复杂动力系统，理论计算同宿(或异宿)轨道的参数方程较为困难，可以采用函数逼近的思想去近似模拟。帕德逼近方法[6]是一种基于高阶泰勒展开构造设解函数的特殊方法，它以有理函数作为逼近工具，可以很好地克服泰勒展开在实际应用中的不足之处。

由图1可知，x（t）为偶函数且有以下初值条件：

设 x （t）在不同时间t处的级数展开式为

将（11）式代入（3）式可得

将（11）式和（12）式写为类帕德逼近多项式（QPA）的形式为

图2 同宿轨道的类帕德逼近解（右支）Fig.2 The Quasi-Pade approximation of homoclinic(right branch)

将上式与（11）式和（12）式的泰勒级数展开进行对应比较后可得 α0=0，α1=21.5，β1=1，因此同宿轨道参数方程的类帕德逼近函数为：

图2是类帕德逼近解（QPA）与Runge-Kutta数值解（R-K）的对比，可以看出类帕德逼近得到的参数方程与精确解基本一致。

将（15）式代入（7）式即可求出梅尔尼科夫函数的简单零点。

2.2 高斯—勒让德方法

如果只需计算梅尔尼科夫函数的简单零点，不关注轨道参数方程解的具体形式，可以绕过参数方程的求解，通过对Hamilton量做一些变换，将积分转化到易于计算的积分域上[7]。由（4）式可得

在同宿轨道上，对上式分离变量得

其中：x0是同宿轨道与x轴的交点。

将（17）式代入A和B的表达式可得

其中：xi为鞍点。为了计算积分A和B，将积分域 [x0,xi]均匀划分N个子区间。设其中某个子区间为[a,b]，则在[a,b]中选取三个高斯点可按下式进行：

三个高斯点对应的权重系数分别为 w1=0.555 6，w2=0.888 9，w3=0.555 6。取 α=0.5，β=-1，γ=1，外激励频率变换区间为0～1.5 rad/s。在计算B时，内外积分域应分别划分子区间，本文中内部积分域划分50个子区间，外部积分域划分100个子区间。最终得到的计算值见图3。采用Gauss-Legendre积分的优点在于，无需重新构造差值函数再进行数值积分，直接利用Gauss-Legendre公式的离散形式即可。此外，高斯积分点本身就是不等分积分点，因此具有较高的计算效率和精度。

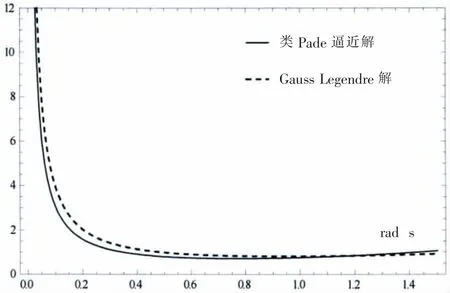
图3 混沌阈值曲线（类Pade逼近解与Gauss-Legendre解）Fig.3 Chaos threshold curve(QPA versus Gauss-Legendre)

由于类Pade逼近得到的轨道参数方程与精确解几乎无差异，图3中类Pade逼近解可作为精确解。Gauss-Legendre解比类Pade逼近解稍大。由于Gauss-Legendre方法在计算梅尔尼科夫函数零点时易于实施，在不需要轨道方程的参数解时可以采用Gauss-Legendre方法。

2.3 数值验证

由梅尔尼科夫函数计算出一阶零点只能说明系统存在不变集Λ，这只是系统出现混沌的必要条件[8]。下面将通过数值计算方法即Lyapunov指数谱对结果进行进一步分析。

Lyapunov指数表示系统在经过充分长时间的演变后，单位时间内所引起的指数分离[5]。对于本文中连续的微分动力系统，选取RHR算法[9]，并对ω=1 rad/s这一激励频率进行验证。由上文计算可得，ζ＞0.811 1α即ζ＞0.406时系统可能出现混沌。分别计算ζ1=0.35和ζ2=0.45时系统的Lyapunov指数，数值计算结果见图4。

图4 不同激励幅值下Lyapunov指数谱Fig.4 Lyapunov exponents of different excitation range

从图4中可以看出，当激励幅值小于混沌阈值时，系统的最大Lyapunov指数小于零，轨道会收缩并最终趋于稳定值。当激励幅值大于混沌阈值时，系统的最大Lyapunov指数大于零，表示轨道分离，运动已不再稳定。

3 船舶非线性横摇动力系统

作为一单自由度的动力系统，船舶横摇的非线性体现在阻尼力矩的非线性和恢复力矩的非线性。该横摇方程的表达式见下式：

其中：Jφφ和ΔJφφ为转动惯量和附加转动惯量，为阻尼项，

因船舶横摇运动的左右对称性，非线性恢复力矩中只有奇次方项。可通过对消灭曲线拟合得到。（21）式两边同除以 （Jφφ+ΔJφφ）可得

在（21）式引入小参数 0＜ε＜＜1，则有

表1 某型船主要参数列表Tab.1 List of parameters of ship

选取某型船[10]，船型参数见表1。

该横摇系统的正则方程形式为：

系统的相图和势函数见图5。图中sl是左鞍点，sr是右鞍点，c是中心点。sl和sr即对应横摇的稳性消失角，其中sl=-sr=-1.543 rad。

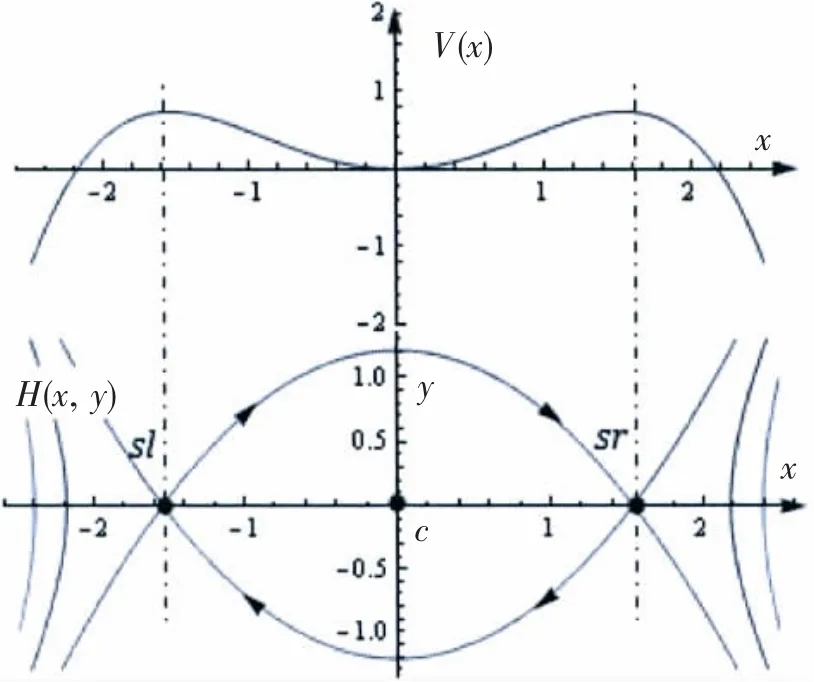
图5 船舶横摇系统的相图和势函数Fig.5 Phase plan and potential function of ship-roll system

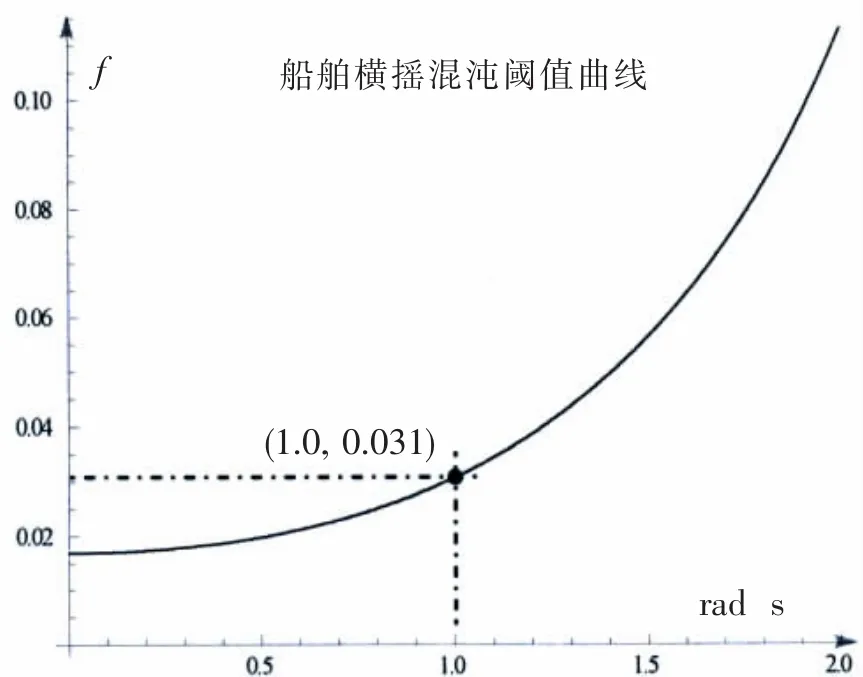
图6 船舶横摇系统的混沌阈值曲线Fig.6 Chaos threshold curve of ship roll system

该横摇系统的梅尔尼科夫函数为：

将表1中参数代入上式，波浪频率范围取Ω∈ [0～2.0 rad/s]，将积分域从时间域转到空间域并设置适当的子区间和高斯积分点可得到该系统的混沌阈值曲线，见图6。

选取波浪激励频率Ω=1.0 rad/s下的混沌阈值进行数值验证，此时激励幅值的阈值为0.031。选取不同的激励幅值计算得到船舶横摇的安全池见图7-9。

从图中可以看到，当激励幅值小于阈值时，横摇系统的安全池完整，随着激励幅值的增大，安全池逐步发生破损。在破损域中选取a、b两点作为初值计算得到的相轨迹见图10。从a、b两点出发的相轨迹绕中心点逐渐振荡发散，当横摇角达到左鞍点即稳性消失角时，横摇角和横摇角速度将持续增大，此时倾覆发生。

图7 横摇安全池（f=0.025）Fig.7 Safe basin(f=0.025)

图8 横摇安全池（f=0.04）Fig.8 Safe basin(f=0.04)

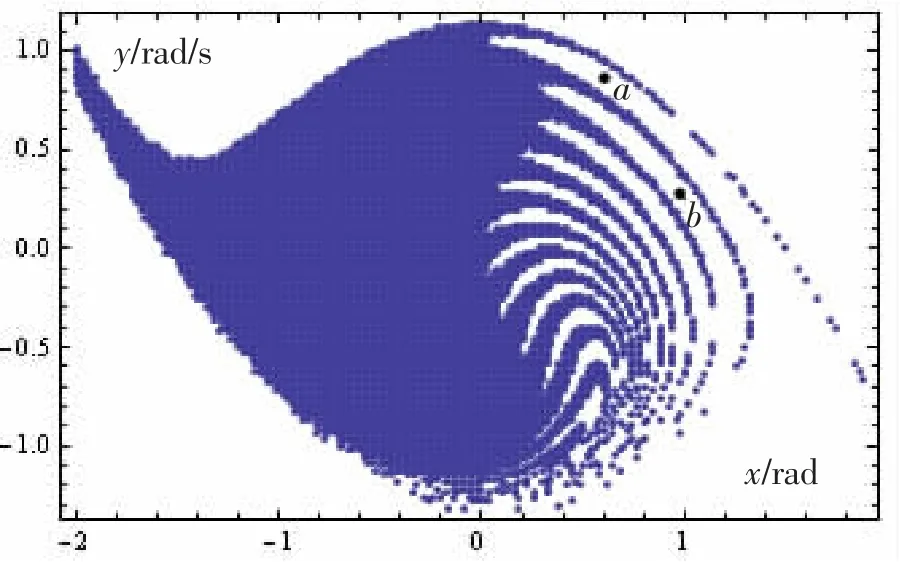
图9 横摇安全池（f=0.08）Fig.9 Safe basin(f=0.08)

图10 破损点的相轨迹Fig.10 The phase trajectory of breakage points

4 结 语

梅尔尼科夫方法是预测非线性动力系统出现混沌阈值强有力的解析方法。针对在求解梅尔尼科夫函数积分时遇到的困难，本文采用了类Pade逼近和Gauss-Legendre积分两种处理方法，并对比分析了两种方法的计算结果及各自的优缺点。在不需要轨道参数方程的具体形式时，可以采用易于工程计算的Gauss-Legendre积分。作为验证，采用时域仿真计算了系统的Lyapunov指数谱。最后采用梅尔尼科夫方法对某船舶的横摇动力系统进行分析，得到了横摇混沌阈值曲线，观察了安全池随激励幅值增大而逐渐破损的过程，并选取破损域中的点计算了相轨迹。本文工作对于研究船舶倾覆机理，进行稳性评估有一定意义。