上凸型内孤立波场中顶张力立管极值响应分析

张 莉 ， 郭海燕 ， 李 朋 ， 王增波

（1.山东科技大学 土木工程与建筑学院，山东 青岛266590；2.山东省土木工程防灾减灾重点实验室，山东 青岛266590；3.中国海洋大学 工程学院，山东 青岛 266100；4.海洋石油工程（青岛）有限公司，山东 青岛 266520）

0 引 言

内孤立波是存在于海洋密度跃层中的非线性大振幅重力波，在其传播过程中能引起具有较大剪切作用的水平流，从而对柔性海工结构物构成严重威胁。海洋立管是海上油气开发中不可或缺的关键构件[1-2]，通常承担钻井、完井、修井、输送油气等重要作业任务，常见的一种结构形式是顶张力立管（Top Tensioned Riser，简称TTR）。顶张力立管的顶部一般会被施加预张力，其上部连接海面平台，下部连接海底井口的锥形节点或应力节点。贯通海底和海面的顶张力立管，极易受到内孤立波所引起的强烈剪切作用的影响。

目前，已有许多学者就下凹型内孤立波对海工结构作用问题进行了研究，但对上凸型内孤立波的影响研究很少。蔡树群等[3-4]首次采用Morison公式，计算了内孤立波对小直径圆柱形桩柱的作用力和力矩，并指出其作用力和力矩远大于表面波的。谢皆烁等[5]基于二维欧拉方程建立流体非线性连续分层模型，计算了内孤立波作用下小直径桩柱上的力和力矩，认为不论内孤立波与海流的方向是否一致，前者作用力都大于后者作用力。黄文昊等[6]针对内孤立波与圆柱型结构的相互作用特性开展了系列实验并建立了内孤立波荷载模型，为常用海洋平台在内孤立波荷载作用下计算提供了一定依据。蒋武杰等[7]用振型叠加法研究了顶张力立管在下凹型内孤立波与非均匀海流共同作用下的多模态振动，认为下凹型内孤立波与海流耦合效应不可忽视。郭海燕等[8]分析了顶张力立管在下凹型内孤立波、表面波和顶部浮式装置运动联合作用下的动力响应情况，指出内孤立波的影响远比表面波和浮体运动的影响大。樊洪海等[9]基于Euler-Bernoulli理论，计算了内孤立波作用和顶部浮体运动导致自由悬挂立管的动力响应，同样只考虑了下凹型内孤立波。

然而，实际层化海水中存在上凸型和下凹型两种内孤立波。在深水区，由于存在浅跃层，内孤立波大多是下凹型；当传播到浅水区时，在非线性作用下，下凹型的内孤立波会转化为上凸型[10]。早前在各海域观测到的下凹型内孤立波较多，近期部分文献报道我国南海北部发现了大量上凸型内孤立波[11-13]。观测资料表明，强非线性上凸型内孤立波最大振幅可达40 m[14]，对海工结构物有显著影响，所以只考虑下凹型内孤立波的影响并不全面。

因此，本文拟建立上凸型内孤立波作用下顶张力立管运动方程，运用有限元方法求解方程，并编制程序对立管运动过程进行模拟。采用我国南海西北部海域的观测数据，研究上凸型内孤立波引起立管的位移、弯矩、应力和顶底端转角等动力响应规律，并讨论不同因素对立管响应的影响，为海洋立管的工程设计提供参考。

1 数值模型

1.1 顶张力立管在内孤立波作用下控制方程

建立如图1所示坐标系。以立管未变形的位形为z轴，向上为正，取立管底部为坐标原点，x轴水平向右为正，内孤立波沿ox轴传播。仅考虑立管受内孤立波来流向的流体力，因而立管的变形和内孤立波引起的流速均在oxz平面发生。顶张力立管装有张紧设备的上端与上部浮体铰接，下端与井口的万向节铰接，可以将其视为受张力的简支梁。由于立管顶部张力作用，建模时可以假定立管线弹性、小变形。根据达朗贝尔原理可以得到顶张力立管顺流向控制方程[15-16]

其中：mr为单位长度立管质量；mi为单位长度管内流体质量，ma为外部流体附加质量，为附加质量系数，ρe为外部海水的密度，D 为立管外径；C 为结构阻尼；C′为水动力阻尼，C′=ρeCdDu，Cd为曳力系数，u为内孤立波引起的水平流速；为立管的加速度，为立管的运动速度；E为立管的弹性模量，I为截面惯性矩；Te为有效张力；f′为流体作用力为内孤立波引起的海水加速度，为海水相对于立管结构的速度。

1.2 内孤立波数值模型

假定海水密度的垂向分布是两层结构，这种近似虽然简单，但却是一般中、低纬度浅海区域春夏秋三季层化状况的粗略近似[10]，具有实际意义。设上层海水的密度和深度分别为ρ1和h1，下层海水的密度和深度分别为ρ2和h2，水深h=h1+h2，内孤立波振幅为η0。坐标如图1所示，根据两层密度分布假设，有KdV理论解内孤立波界面位移表达式[11]（不计浅水项和耗散项）：

其中：η0为内孤立波振幅；φ是内孤立波相位角，φ=为内孤立波相速度，，Δρ、ρ是上下两层流体的密度差与平均密度，分别为：；l为特征长度，l≈

由水动力学、流体连续方程结合波面方程可以得到内孤立波引起的水平方向速度和加速度。

图1 顶张力立管分析模型及受力情况Fig.1 Sketch of a TTR under loads

内孤立波引起的水平速度：

内孤立波引起的水平加速度：

1.3 运动方程的边界条件

立管模型顶底端均为铰接，因而边界条件分别为：

1.4 有限元离散及方程求解

采用Galerkin方法对立管控制方程进行离散，最终得到单元刚度方程：

将各单元刚度矩阵组合至整体刚度矩阵，即得到顶张力立管在内波场中的有限元方程组：

其中：[M]、[C]、[K]分别为立管系统的整体质量矩阵、整体阻尼矩阵和整体刚度矩阵；为立管每一个节点上的顺流向加速度、速度、位移列阵；｛F｝为整体荷载列阵。

在时域内求解方程，采用Newmark-β法进行逐步积分求解，即只要给出ti时刻的位移xi、速度和加速度，可计算出经过Δt时间后 ti+1时刻的解 xi+1、和，进而可推算出内孤立波作用下顶张力立管所有时刻的位移、弯矩、应力、转角等动力响应。

2 计算过程与程序验证

基于上述计算方法，用MATLAB编制相应计算程序，输入上凸型内孤立波要素和立管的相关参数，即可得到立管的响应。计算流程如图2所示。

图2 上凸型内孤立波作用下顶张力立管分析计算流程图Fig.2 Flow chart of the riser dynamic analysis under elevation ISW

因上凸型内孤立波发生时间不可预见并且观测难度较大，目前尚无上凸型内孤立波经过时立管响应的实测数据，所以用文献结果与本文进行对比验证。

（1）采用文献[14]中的内孤立波参数，将本文程序计算得到的水平流速与文献进行对比，如图3所示。其中（a）为文献结果，（b）为本文计算结果，由图可得，上下两层流体中水平流速随时间变化的情况同步，程序计算所得最大流速（上层0.57 m/s、下层0.71 m/s）与文献结果基本相等，流速方向也完全一致。

（2）为验证流体力作用下顶张力立管动力响应计算的正确性，采用文献[17]中的数据对线性波浪作用下顶张力立管位移进行分析，并将计算结果与文献进行对比，如图4所示。其中，（a）图中带“×”标记的线条为文献中的时域分析结果，本文时域计算结果（b）图与其振动形态近似，无量纲最大位移包络图也能较好地吻合，从而说明本文方法及计算程序可靠。

图3 内孤立波引起的水平流速与文献的对比Fig.3 Comparison of the simulated horizontal flow velocity induced by ISW with the result of other paper

图4 波浪作用下立管响应与文献的对比Fig.4 Comparison of the riser response under wave with the result of other paper

3 算例分析

3.1 算例数据

假设立管均质且壁厚沿管长不变，沿用上文中各变量的定义，立管参数见表1（表中CM和Cd的选取依据规范API-RP-16Q）。流场参数采用文献[14]中实际观测到的上凸型内孤立波数据，见表2。

表1 立管参数Tab.1 Dimensions and coefficients of the TTR

表2 上凸型内孤立波参数Tab.2 Properties of elevation ISW

3.2 上凸型内孤立波引起的立管响应

图5为计算得到的上凸型内孤立波经过时立管无量纲位移包络图和弯矩包络图。由图5可知，立管在上下层流体中段附近各有一个极值，下层流体中的响应大于上层流体中的响应，两层流体分界面附近位移响应最小。全长最大位移在距海底32.17 m处，其绝对值为1.77D；全长最大弯矩处于距海底27.79 m 处，为 33.45 kN·m。

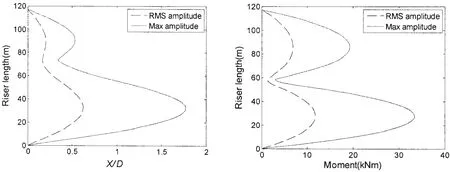
图5 顶张力立管无量纲位移包络图及弯矩包络图Fig.5 Envelopes of dimensionless displacement and moment for the TTR

立管设计时要求最大等效应力不大于屈服应力的2/3[18]，因而本文对上凸型内孤立波作用下顶张力立管的应力进行了计算，得到应力包络如图6所示。由图6分析可知，立管应力分别在上下层有一个极值，最大应力发生在距海底27.79 m处，为36.56 MPa。立管张力从顶端向下逐渐减小，因而位移、弯矩和应力极值均出现在立管偏下部分。

为防止节点破坏，立管设计规范API中规定钻井模式下的立管顶底部柔性接头平均转角不大于2°，最大转角不大于4°[18]。当上凸型内孤立波经过时立管顶底端转角随时间变化的情况如图7所示。由图7可知，顶端转角先增大后减小为0°，方向有一次反转，这与上层流体中的立管位移方向有一次变化相对应；底端转角经历由0°逐渐增大到极值再缓慢减小至0°的过程，顶端极值为0.56°，底端极值为1.54°。如果考虑内孤立波经过时上部浮体运动所引起的立管运动，立管转角可能会超过设计允许值，应当引起注意。

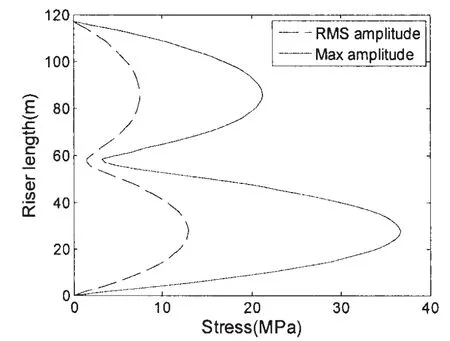
图6 顶张力立管应力包络图Fig.6 Envelopes of stress for the TTR

图7 立管顶底端转角时程曲线Fig.7 Time history of the angles at top and bottom ends

图8为距海底分别为16 m、32 m、48 m、65 m及91 m处立管位移的时程曲线。其中16 m、32 m和48 m均处于下层流体，其位移随时间的变化基本同步，均在波峰经过时达到极值，并且都沿-x方向发生位移；65 m处为上下两层流体的分界线，此处位移较小，在波峰经过前其位移方向基本同下层流体中的立管（-x方向），但在波峰将要离开时发生反方向位移；91 m处为上层流体的中间，其位移（-x方向）首先增大后减小，在波峰到达之前位移减为0，接着发生反方向位移；很明显，位于两层流体分界面及其以上部位的立管位移方向发生了一次逆转。

从图8可看出，立管的位移主要发生在400-800 s之间，为更全面地研究立管位形变化情况，图9呈现了这段时间内的立管全长位移。由图9分析可知，在上凸型内孤立波逐渐靠近立管直至离开的过程中，位于下层流体中的立管位移逐渐增加到最大，再逐渐减小至0，位移方向始终与下层流速方向相同（-x方向）；由于下层流速略大于上层流速，位于上层流体中的立管首先发生与下层流速同向的位移，随着上层流速的逐渐增大，流体作用力导致立管上半部分-x方向位移逐渐减小并发生反向位移（x方向），整个立管呈现“S”型；随着内孤立波逐渐远离，最终全长位移归为0。

图8 不同深度处立管位移时程图Fig.8 Time history of displacement in different depth

图9 400 s、500 s、600 s、700 s和 800 s时立管全长位移图Fig.9 Displacements in 400 s,500 s,600 s,700 s and 800 s

3.3 不同因素对顶张力立管极值响应的影响

不同振幅内孤立波引起的流场不同，进而导致立管响应有差异。分别选取内孤立波振幅等于15 m、25 m、35 m、45 m和55 m，得到立管全长的位移状态，如图10所示（Amplitude表示内孤立波的振幅）。当振幅等于15 m、25 m、35 m、45 m和55 m时，对应的立管全长最大位移分别为0.30D、0.90D、1.77D、2.93D和4.37D。可见位移响应随着内孤立波振幅的增大而增大，位于下层流体中的立管位移增幅大于上层流体中的。

通常海水密度并不恒定，上下层流体之间的密度差也会影响立管极值响应。图11讨论了密度差的影响，上层密度1 022 kg/m3保持不变，令下层密度分别为1 024 kg/m3、1 025 kg/m3、1 026 kg/m3、1 027 kg/m3和 1 028 kg/m3（即上下层密度差为 2 kg/m3、3 kg/m3、4 kg/m3、5 kg/m3和 6 kg/m3），得到立管的最大位移分别为0.88D、1.33D、1.77D、2.20D和2.66D。很明显，随着上下层流体密度差的增大，立管全长位移也跟着增大，上下层流体中的位移方向依然相反。从公式（3）中也可看出，密度差增大会导致上下层流速同时增大，从而流体对立管作用力也增大。

作为顶张力立管设计过程中的重要参数之一，顶部张力的大小直接影响立管的响应大小。图12表示顶部施加张力不同时立管全长位移，当顶部张力分别为1.1Te、1.3Te、1.5Te、1.7Te和1.9Te时，立管最大位移分别为1.77D、1.57D、1.41D、1.29D和1.19D，立管下半段对顶张力的变化更敏感。随着顶部张力的增大，相当于增加了立管的刚度，位移相应减少。因而在内波频发海域，可通过增加张紧器中的张力来改善立管的性能，但张力的增加会引起顶部应力集中。

图10 不同内孤立波振幅引起的全长位移Fig.10 Displacements under different amplitudes of ISW

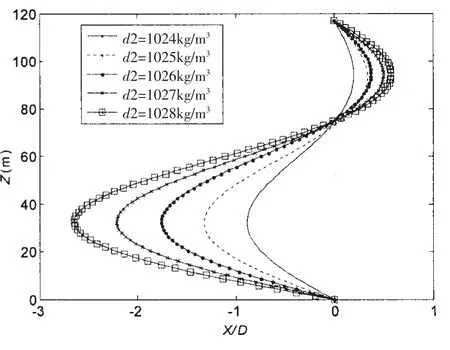
图11 不同海水密度比下立管的全长位移Fig.11 Displacements under different density ratio

图12 不同顶部张力下立管的全长位移Fig.12 Displacements with different top tension

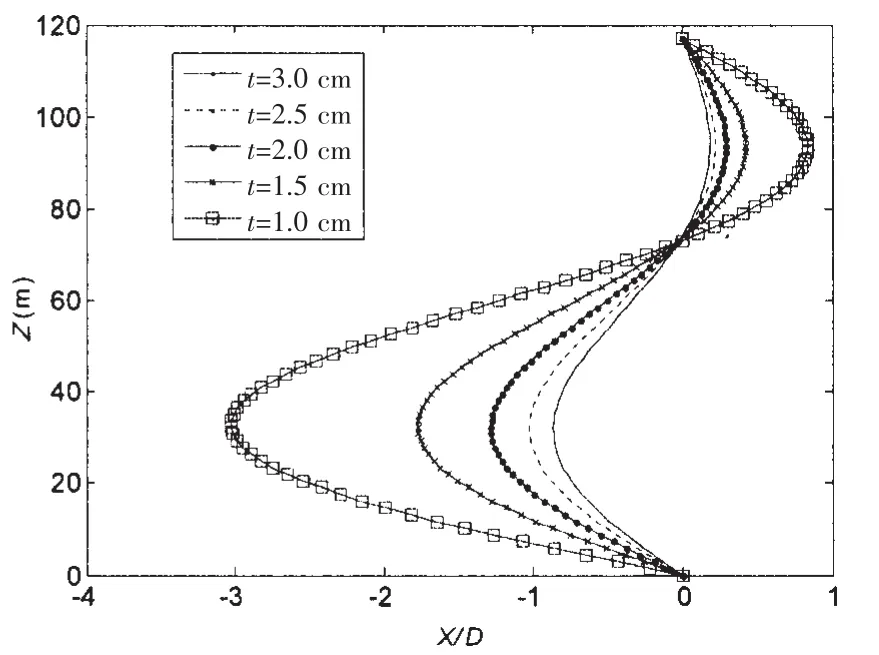
图13 不同壁厚下立管的全长位移Fig.13 Displacements with different wall thickness

图13为考虑立管壁厚对立管位移响应的影响。壁厚分别选取3.0 cm、2.5 cm、2.0 cm、1.5 cm和1.0 cm，立管最大位移分别为0.86D、1.00D、1.28D、1.77D和3.00D。立管的壁厚是一个重要设计参数，设计可能有内孤立波经过海域的立管时，在允许范围内，立管壁厚应尽可能厚一些，以增加其刚度，减小位移。

4 结 论

本文基于KdV方程，参照南海实测数据，对上凸型内孤立波作用下顶张力立管的动力响应做了数值模拟，采用Newmark-β法实现有限元模拟的时域分析，得到了上凸型内孤立波作用下顶张力立管的无量纲位移、弯矩、应力包络及顶底端转角；并对上凸型内孤立波振幅、上下层流体密度之差、顶张力和壁厚对立管响应的影响进行了分析。

研究结果表明：上凸型内孤立波使位于上下两层流体中的顶张力立管位移、弯矩、应力及顶底端转角增大，但在两层海水分密度界面附近影响相对较小，另外，内孤立波对立管中下部的受力及响应有显著影响。位于下层流体中的立管仅发生-x方向位移，位于上层流体中的立管先发生短时小幅度-x方向位移再反方向运动。由于这一密度分层海域上下层水深相当，上凸型内孤立波引起的剪切作用剧烈，导致立管位形呈现"S"型，而增大立管顶部的张力或者增大立管壁厚能减轻上凸型内孤立波的作用。