二维多翼翼型中拱线设计方法理论研究
2019-03-14陈玮琪王宝寿
蒋 旭 , 陈玮琪 , 王宝寿
(1.上海交通大学 海洋工程重点实验室,上海 200240;2.中国船舶科学研究中心,江苏 无锡 214082)
0 引 言
在工程应用中,经常会遇到多翼结构或多翼问题,比较重要的有栅格翼、地效翼。栅格翼是由许多薄翼镶嵌在边框内形成的多翼结构[1]。如图1所示,其主要结构形式包括两种,即框架式和蜂窝式。栅格翼广泛地应用在航空航天与水下兵器领域,如R-77空空导弹、美国MOAB炸弹、猎鹰9号火箭、“联盟号”宇宙飞船救生逃逸系统、中国CZ-2F飞船逃逸救生系统、俄罗斯Club潜射巡航导弹、印度SLCM潜射巡航导弹等;地效翼也被归结于多翼领域则是因为在其理论研究中,地效翼和其关于地面或水面镜像对称的假想翼共同组成双翼问题,如图2所示,也可视为一种多翼结构。
本文将类似栅格翼或地效翼的绕流问题统称为多翼绕流问题。然而针对多翼问题的研究多是在给定翼型条件下对其流体动力性能的建模和计算,可视为一种正问题;如多翼的气动特性研究中,陆中荣等[2]将涡格法推广应用于计算外形复杂的蜂窝式栅格翼的气动特性;陆中荣等[3]采用氢气泡法和丝线法在风洞和水洞中开展栅格翼相关实验,研究其扰流特性;邓帆等[4]采用风洞实验和数值计算的方法,分别对不同翼弦格宽比的栅格翼及不同后掠方式的栅格翼进行了研究;沈瑕龄等[5]给出了计算栅格翼和机身组合体亚超音速气动力干扰理论方法;多翼的水动特性研究中,黄涛[6]采用商用软件FLUENT计算了栅格翼在雷体上应用时的水动特性;姚琰等[7]在空泡水洞中对6种栅格翼进行了实验,得到了栅格翼流体动力系数随空泡数的变化规律;夏艳艳等[8]开展了栅格翼外框剖面形状和格片数量对其流体动力特性影响的实验研究;陈玮琪等[1]对超空泡栅格翼进行理论建模,并揭示了叶片间隙的空泡对水动力的干扰机理。而关于给定流体动力性能后设计多翼翼型的研究则较为少见,在实际工程应用中,多翼翼型多是直接选用已有的单翼翼型,还没有多翼翼型设计理论可以参考。而与之相对应的单翼翼型设计问题早已形成了一套系统的设计理论,其中美国的国家航空咨询委员会早在上世纪30年代后期就对翼型的性能做了系统的研究[9],提出了NACA四位数翼族和五位数翼族。其主体设计思路是:如果翼型不太厚,可以将翼的弯度作用和厚度作用分开来考虑,分别设计翼型的弯度和厚度,大大降低了翼型设计的难度。厚度设计上,各国从经验上获得的良好翼型,如果将弯度改直,即改成对称翼型,且折算成同一厚度的话,其厚度分布几乎是一致的,于是就采用了这个当时认为最好的厚度分布作为NACA翼型族的厚度分布;弯度设计上,即翼型的中拱线设计。在薄翼理论中,中拱线的作用通过连续分布的涡来代替,给定边界条件即可求得相应的涡强分布。反之,则可以指定涡强分布来反推中拱线,这也是NACA系列翼型中拱线的设计思路。
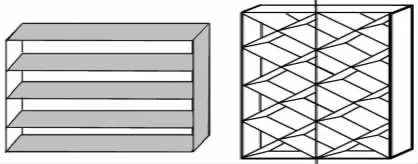
图1 栅格翼结构形式Fig.1 Structure of grid fin
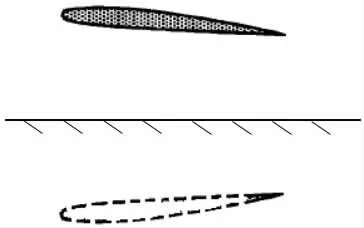
图2 地效翼模型示意图Fig.2 Schematic of model about WIG
以上NACA系列翼型的设计仅是针对单翼翼型的设计,而在多翼问题中,翼之间还会存在绕流的干扰效应[10],直接应用NACA单翼翼型到多翼结构中,可能会导致流体性能达不到相关要求。针对这一问题,本文希望建立一种多翼翼型的设计方法。因为翼的几乎所有重要的力学参数(升力、力矩和压力中心等)都与中拱线的形状密切相关,翼型厚度仅影响翼的阻力,且厚度设计影响因素较为复杂,因此在这里仅对多翼翼型中拱线进行设计。具体地,针对二维多翼绕流问题进行建模,并参考NACA翼型中拱线的设计思路,从均化翼型载荷(压力差分布)的角度出发,考虑多翼之间的干扰效应,形成了一种关于多翼翼型中拱线的设计方法,并将其应用于地效翼和栅格翼的中拱线设计当中。
1 准备知识
1.1 NACA单翼翼型中拱线设计思路
不失一般性,将来流速度V∞和弦长c均设定为无量纲的单位1,则基于无限流场线性薄翼理论,在翼的弦线上布涡并结合中拱线上的边界条件,可以确定涡强分布γ(ξ)的积分方程[11]

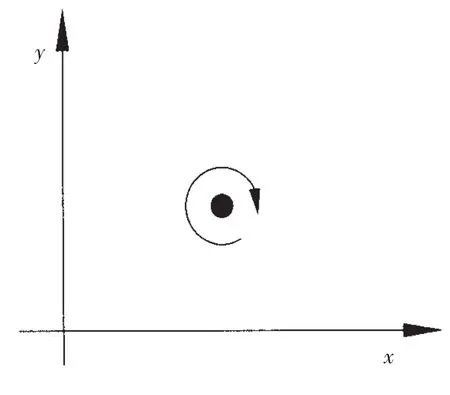
图3 坐标系选取Fig.3 Choice of coordinate

图4 平板涡强分布Fig.4 Vortex distribution on the plate
翼型设计中的一个关键目标就是使翼型载荷均匀分布,以平板翼型为例,其绕流的涡强分布结果如图4所示,根据线性薄翼理论,翼型载荷Δp(上下表面压力差)和涡强成正比,

可以看出平板绕流中其载荷分布Δp主要集中在导边附近,而且在导边处出现奇点,载荷趋于无穷大。这样会对翼型的结构和流动产生诸多不利的影响。
因此在保证升力大小和方向不变的情况下,希望能通过改变中拱线形状的方法使载荷分布更均匀些。在理想情况下,当然希望载荷在中拱线上均匀分布,但是这样会在随边不能满足库塔条件,因此通过放宽随边附近载荷的要求,以及假定在该点涡强为零,可以求得更为实际的翼型[12]。属于这类最简单翼型的是NACAa系列,它由导边开始至下游的一段距离a内的载荷为常数,随后就线性衰减,如图5所示,其中a=0.2-0.8和cli=0.2。
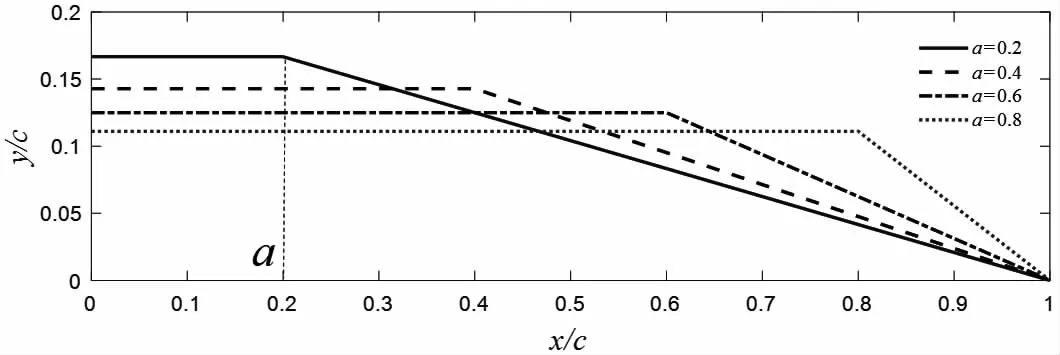
图5 线性化涡强分布Fig.5 The linear vortex distribution
针对图5所示的线性化涡强分布,可根据积分方程(1)求出翼型中拱线外形表达式,即[13]
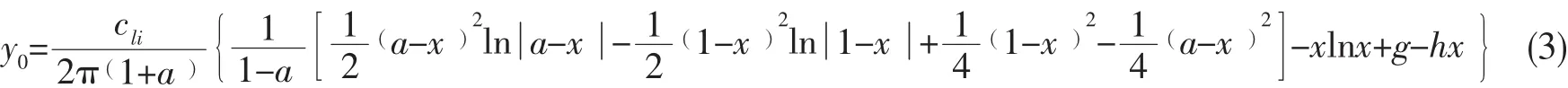
对应于图5的涡强分布,根据(3)式计算出的NACAa系列翼型中拱线见图6所示。
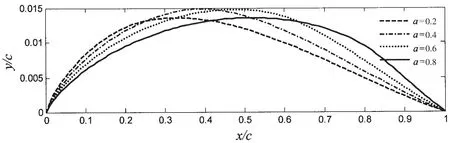
图6 NACAa系列翼型中拱线Fig.6 The meanline of the NACAa series wing
1.2 多翼中拱线设计思路
今将单翼中拱线设计思路推广到多翼设计中去。众所周知,单翼的线性薄翼理论中,载荷仅与当地涡强成正比。下面将证明,在多翼问题中,每片翼的载荷也仅与当地涡强成正比。这个结论是后续多翼中拱线设计方法的一个关键。
设仅当每个翼的涡分布为γi(x)时,才能保证达到给定值Δpi(x)。观察n个多翼中第j个翼的翼上下表面水平扰动速度

其中:(4)式两式的第二项为除j翼外,其余多翼涡系于j翼的(x,0)处引起的诱导速度水平分量,且Δui+≡Δui-。根据线性理论和伯努利方程,上下压差可表示为

由此可以看出多翼问题中,每片翼的载荷仅与当地涡强成正比。因此,在多翼中拱线设计中,如果指定翼的载荷分布,相当于给定了翼上的涡强分布。
2 镜像对称双翼中拱线设计(地效翼)
基于上节介绍的单翼绕流中拱线设计方法,结合多翼绕流的特点[10],可以较为方便地将相应中拱线设计方法推广到多翼当中去。首先考虑以地效翼为代表的镜像双翼的中拱线设计方法。
2.1 地效翼中拱线设计方法
二维地效翼理论研究中,如图2所示,往往是将真实的效翼及其关于地面或水面镜像对称产生的虚拟翼共同组成一个特殊双翼系统。此双翼系统的翼型设计可以仿照单翼翼型的设计,同样在双翼弦线上分布点涡,结合相应中拱线上的边界条件可以得到积分方程

其中:h12是两翼之间的垂向距离,地效翼理论研究中h12则是翼距地面或水面距离h的两倍,上式本应该是两个方程组成积分方程组,因为两条中拱线满足的方程相同,这里只列出一个。可以看出双翼和单翼的区别仅是右端多出了一个积分项,这样如果参考单翼的设计思路,从均化载荷的角度出发,并回避均布载荷方案产生的随边奇点的缺点,直接采用线性化载荷方案,结合单翼计算出的中拱线(3),这里只需对右端多出的积分项再次积分即可求出中拱线坐标的附加项,即

地效翼直接采用线性化载荷方案,即线性化涡强分布如图5所示,上式可以表示成:
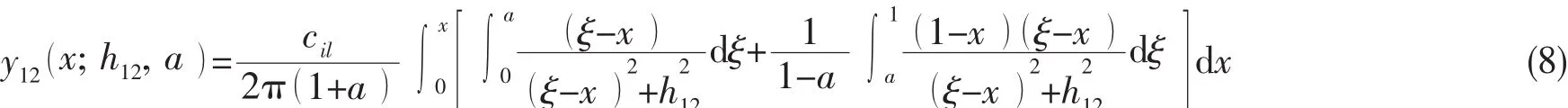
上式结果为
根据(6)式,结合单翼坐标 y0((3)式)以及双翼坐标附加项 y12((9)式),可以很容易地得到设计地效翼的坐标,即

上式即为设计的地效翼翼型,可以明显看出翼型主要由两部分组成,单翼翼型与双翼翼型附加项,且前者是是弦向坐标x与线性载荷参数a的函数,附加项y12在此基础上还是双翼垂向间距h12的函数。为了与物理实际联系起来,将附加项y12定义为干扰项坐标。而且从(10)式中可明显看出,设计的地效翼翼型是这两者的差值,而且可以从图7中看出设计翼型的拱度相对单翼翼型要小。从物理上解释,双翼绕流不同于单翼绕流,双翼之间还会存在相互干扰,针对地效翼的镜像双翼系统而言,上下镜像对称的两个翼相互增大了来流攻角,使得环量增强,地效翼升力也会相应地增加;另外根据薄翼理论的相关结论,即在零攻角下,翼型拱度越大,翼型升力越大。因此在设计升力系数相同的情况下,地效翼拱度必然小于单翼拱度。

图7 h=0.5,a=0.8时单翼和地效翼翼型中拱线对比Fig.7 Comparison of the mean lines of single wing and WIG at h=0.5,a=0.8
在地效翼翼型设计中,两个参数,即线性载荷参数a和垂向间距h12,这两者的选择很关键,图8和图9分别是在这两参数下设计的中拱线。线性载荷参数a直接决定了双翼中拱线上的载荷分布,a表示均布载荷分布的范围及随边线性卸载的开始;而垂向间距h12则是决定双翼干扰程度的关键参数。值得注意的是设计中拱线在随边的坐标并不为零,有个小的偏移,根据镜像双翼翼型中拱线表达式(10),偏移则是与翼之间的干扰有关。
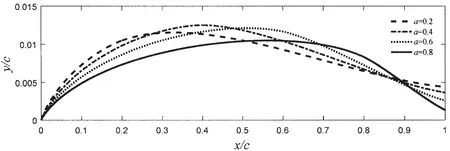
图8 h=0.5时地效翼中拱线随a的变化Fig.8 The mean lines of WIG vs a at h=0.5

图9 a=0.8时地效翼中拱线随间距的变化Fig.9 The mean lines of WIG vs h at a=0.8
以上地效翼中拱线都是在零攻角条件下设计的,其在不同工况(攻角、飞高等)下的流体动力性能还需经检测和验证。对于地效翼而言,其压力中心是影响地效翼动力性能的重要参数。在实际工程应用中,其压力中心对地效应飞机的纵向操纵性和纵向稳定性有着重要的意义[14]。事实上,纵向操纵的目的,即是调节压力中心的位置,保证纵向力的平衡。因此能否保证翼压力中心在不同工况下的稳定,则是考量地效翼翼型好坏的有效指标之一。
针对图8所设计的翼型在不同工况(攻角、飞高等)下的压力中心,本文采用离散涡方法[15]对此进行了计算,取线性载荷参数a=0.8、设计高度h=0.25,计算结果见图 10和图11。
从图10可以明显看出设计翼型的压力中心随高度的变化很小,攻角对压力中心的影响稍大;从图11则可以看出设计翼型可以在均化载荷的同时,保持压力中心变化范围和普通单翼相当,说明本文的设计翼型具有一定的实用价值。

图10 设计中拱线的压力中心在不同攻角下随高度的变化Fig.10 Dynamic centers of the designed mean lines changes with height under various attack angles

图11 设计中拱线与单翼在不同高度下的压力中心对比Fig.11 Comparison of the dynamic centers of the designed mean lines and normal mean lines under various heights
3 平行多翼中拱线设计(栅格翼)
以栅格翼为代表的平行多翼如图12所示,由图中可以看出和地效翼的镜像布置(图2)不同的是,栅格翼各个翼平行布置,且翼的个数不做限制。

图12 平行多翼绕流示意图Fig.12 Schematic of the flow of multi-wing
3.1 平行双翼
相对上节地效翼中拱线的设计,平行双翼的设计有很多相似之处,即同样是上下布置的双翼绕流系统,不同之处则主要体现在上下双翼的布置位置,上节地效翼上下两翼关于地面或水面镜像是对称布置的,而本节所针对的主要是平行布置的双翼系统,同样采用点涡分布法,则上节的积分方程(6)将变为

可以明显看出方程仅仅是在最后的符号上发生了改变,即由地效翼的减号变成了加号,这直接体现了双翼布置位置的差别,因为平行双翼的平行关系,各个翼的绕流状况相同,因此上下两翼布置涡的方向是相同的。由(11)式然后结合上节的结论,同样采用线性载荷方案,可以得到设计的平行双翼的翼型坐标


图13 h12=0.5,a=0.8时单翼和平行双翼翼型中拱线对比Fig.13 Comparison of the mean lines of single wing and double-wing at h12=0.5,a=0.8

图14 h12=0.5时平行双翼中拱线随a的变化Fig.14 The mean lines of double-wing vs a at h12=0.5

图15 a=0.8时平行双翼中拱线随间距的变化Fig.15 The mean lines of double wing vs h12at a=0.8
同样地,双翼的坐标也是由两部分组成,即单翼翼型y0与双翼翼型干扰项y12,只不过右端的符号也变为加号。图13表示单双翼翼型坐标的对比,可以看出平行双翼的拱度相较单翼变大,与地效翼相反,即平行双翼翼型坐标较单翼坐标的增量为双翼干扰项坐标,从物理上解释,双翼平行布置的布局导致双翼绕流相互干扰,升力相互削减[10],在单双翼翼型设计时为保证设计升力系数相同,由于双翼相互干扰导致的升力损失,双翼为弥补这方面的升力损失,只有增加一部分拱度,这个拱度增量则和线性载荷参数a和垂向间距h12相关。线性载荷参数a对双翼翼型坐标的影响体现在图14,可以看出其趋势和地效翼的趋势大致相同;图15则表示的是双翼间距对翼型的影响,其趋势正好和地效翼相关趋势相反。
3.2 平行三翼
以上是关于双翼的设计,包括平行双翼和镜像双翼,本节将上述设计方法推广到栅格翼相关的平行三翼系统,同样在三平行翼的中拱线对应的弦线上布涡,结合相关的边界条件,可得到由三个积分方程组成的积分方程组,即

每个翼的中拱线上给定相同的线性载荷分布,可以求得

图16和图17分别表示按上述设计思路得到的三翼系统在三翼等间距和非等间距时的翼型,可以看到等间距时,外侧两个翼翼型重合,且拱度要小于中间翼型;不等间距时则三个翼型均不相同,且中间翼型拱度最大,与中间相近的翼型次之,外侧偏离中间翼的翼型拱度最小。这里同样要结合多翼系统动力性能计算的结论,翼之间的干扰和翼间距hij有着直接的关系,翼间距越小翼之间的干扰越强,平行翼系统里干扰越强则意味着升力损失越大。

图16 等间距下三翼中拱线Fig.16 The mean lines of three-wing under equal distance
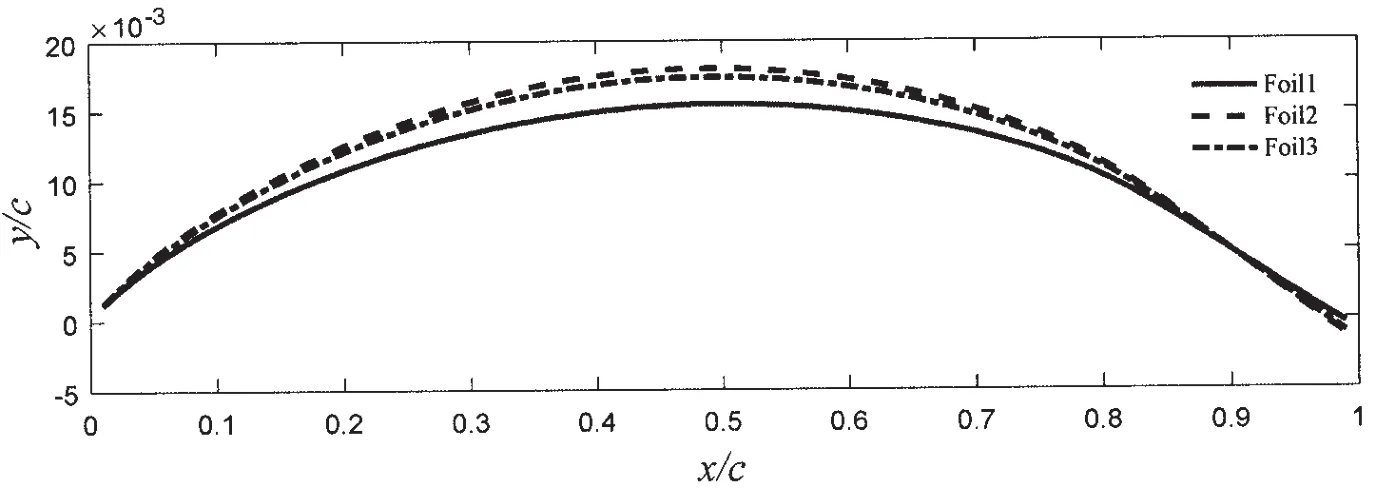
图17 不等间距下三翼中拱线Fig.17 The mean lines of three-wing under unequal distance
3.3 任意多个平行翼
以上对于双翼系统和三翼系统的翼型设计,可以将此多翼中拱线的设计方法推广到任意多个翼组成的多翼系统,假如n个翼组成的多翼,那么相应的积分方程组同样是由n个积分方程组成(这里省略),则最终的各个翼的翼型坐标可以表示为:

这是一个通用公式,只要知道相应的线性载荷参数a和垂向间距hij,就可以设计出任意多个翼组成的多翼中拱线。
4 结 论
本文基于二维线性薄翼理论,从均化载荷的角度出发,考虑多翼绕流干扰效应,对任意多翼且任意给定了每个翼载荷条件下,建立了每个翼的中拱线设计方法,并给出了解析表达式,用于栅格翼和地效翼的中拱线数学求解,并从中得出以下结论:
(1)多翼中拱线主要由两部分组成,一是单翼中拱线,二是多翼之间的干扰项,两者以不同的方式组合即可得到不同多翼布局的翼型中拱线;
(2)二维地效翼作为一种特殊的镜像对称的双翼系统,地效应存在导致升力增加,若保持单翼的载荷,则拱度需减少;
(3)栅格翼是平行多翼,多翼存在导致了升力降低,若保持单翼载荷,则每一片翼需有不同程度的拱度增加。
该多翼翼型设计方法具有解析形式,物理意义明确,影响因素清晰,数学求解方便,对工程估算有重要参考价值。
