国内购买力平价构建及物价水平研究
2019-03-13张迎春周子堰张亚平
张迎春,周子堰,陈 枫,张亚平
(青岛大学 经济学院, 山东 青岛 266071)
一、引言
购买力平价(Purchase Power Parity,简称PPP)理论应用于考察不同国家的货币购买力水平,根据各国不同价格水平计算货币间等值系数,将之作为调整因子(也可理解为虚拟公共货币),用来调整以不同货币表示的各国国内生产总值(简称GDP),使之同度量化,从而实现各国经济实力的比较。近年,该理论由对各国货币购买力平价测度,转化为对同一货币在不同区域购买力水平的测度。其实践意义也由原有的各国经济实力排名,转化为一国内部各区域货币购买能力比较、用名义货币价值表示的收入水平和贫困及脱贫标准等,对货币真实购买能力进行考量。这对于客观评价居民生活水平、制定相关标准,比如差异化的地方个税标准、差异化的地区贫困和脱贫标准等具有重大意义。
国内购买力平价测度源于国际间购买力平价测度,后者是世界银行一项全球性统计活动——国际比较项目(International Comparison Program,简称ICP)的重要产品。该项目是世界上最大的经济统计活动。然而,2015年公布的国际比较结果受到多方质疑,其中关于中国的数据结果不被中国官方所认可。经专家研究认为是大国内部差异导致结果偏颇。因此,世界银行于2015年开始敦促大国进行国内购买力平价测算工作,学界对该问题的研究热情复燃,中国统计部门于2017年开始进行该测度尝试。
国外学者对国内购买力平价测算的关注始于2003年。Dikhanov Yuri测算了菲律宾的国内购买力平价[1],Bettina Aten在计算美国国内购买力平价因子后,重点评价美国个人收入水平变动[2]。Biggeri计算意大利国内购买力平价,重点讨论意大利的贫困程度[3]。国内多数学者将国际比较项目中的购买力平价思想应用于地区差异测度的研究中,其中有地区经济水平差异测度[4-5]、地区贫困程度差异研究[[6-7]和地区消费差异研究[8-9]。官方统计机构的研究成果主要来自“我国地区价差指数方法和应用研究”课题组[10]。
显然,现有的国内外文献皆是侧重将国内购买力平价测度结果应用于不同领域,并未探究方法差异对购买力平价因子数值的影响。所以,购买力平价方法不同,必然对同一实际现象有不同的结论,即方法选择制约并左右了评价结果。本文侧重一种方法的讨论,即利用最短距离法(The Minimum Distance Method,简称MD法)测度中国地区间购买力平价。这是国际间购买力平价测度中的冷门方法,分析发现:其在国内使用时,原有桎梏几近消失,所构建的购买力平价因子更客观。本文首先探讨最短距离法及其在国内使用的新环境和新问题,之后结合实际数据进行实证分析,并评价结果与中国现实的符合程度。
中国地区经济发展极不平衡,等额货币在各地区所具有的购买力也存在显著差异。由于物价水平的不同,对于同一件商品或服务,各地居民利用等额货币所能购买的数量并非相同,生活质量也会因此存在较大差距。鉴于此,在衡量地区间经济差距时,应将价格因素剔除,从而得到反映实际的真实物量指标。因此,本文最终利用购买力平价因子对各省物价水平进行分析,采用省域和八大经济综合区的研究视角,以期为宏观调控提供参考。
二、最短距离法及其应用
最短距离法是图论的经典算法,常应用于计算机、通信等领域,旨在一个连通加权的复杂网络中寻求最优路径。追求全局或者整体路径最优的是最小间隔树法(The Minimum Spanning Tree Method,简称MST),它由澳大利亚学者罗伯特·希尔(RobertJ Hill)博士于1993年引入,初衷是希望能将消费结构、经济发展模式更为相近的国家进行双边比较,再进一步链接形成多边比较,由此得到更为可靠的结果[11][12]109-120。MST致力于构造全局或整体最优路径,使对比国的组合在整体上最佳,却不能使任意两两地区的比较距离最短。为弥补此缺陷,Rao将最短距离法引入到国际比较领域中[13]。
(一)最短距离法的计算过程分析
国内购买平价测度的基础数据是各地区规格品价格及消费支出比重。根据ICP测度框架,GDP被逐级分解为主要总量、大类、中类、小类和基本类,其中基本类是可以获得支出权重的最低层级,其下为具体规格品。计算购买力平价需要规格品价格和基本类以上各项支出比重数据,前者用于计算基本类购买力平价,后者用于将基本类购买力平价汇总至GDP层面,得到最终购买力平价因子,并将其进一步用于不同领域分析。
1.基于Jevons指数的基本类购买力平价计算。基本类购买力平价主要依据各商品或服务项目的价格数据来测算,即对基本类下所有商品的价格比值进行简单几何平均。
2.基于费暄指数的基本类以上层面购买力平价的计算。基本类以上层面购买力平价测度需以各基本类的消费支出为基础,将其作为权重,利用拉式指数(Laspeyres Index)、帕式指数(Paasche Index)、费暄指数(Fisher Index)对各基本类购买力平价进行加权汇总,具体可分为五个步骤。
步骤一:计算拉式指数(以基准地区支出为权重)和帕式指数(以对比地区为权重),对于n个地区来说,可得到n阶拉式指数和帕式指数矩阵。分别表示为:
(1)
(2)
拉式指数以基准地区支出结构为基础,计算各基本类购买力平价的调和平均值,权重为基准地区各基本类消费比重。帕式指数以对比地区支出结构为出发点,权重为对比地区各基本类消费比重。由于两指数均不满足国家反转检验,故拉式和帕式指数矩阵均为对角线为1的非对称矩阵。另外,根据价格指数的偏误理论可知,拉式指数和帕式指数通常为“实际指数值”的上限和下限[14]30-32,只有对比两国间的消费支出规模相近时,拉式和帕式指数才近似相等,否则二者将会相差过大。
步骤二:计算费暄指数,即拉氏、帕式指数乘积的平方根,可得到n阶费暄指数矩阵为:
(3)
由于拉式和帕式指数分别存在“上偏”和“下偏”的问题,为了对其进行调和,则选择用费暄指数进行平均。作为超越指数的代表,费暄指数是拉式和帕式指数的简单几何平均。目的是尽量平等地对待对比两国,即认为两国的消费支出比重同等重要,消除拉式指数和帕式指数的误偏问题。另外,费暄指数满足国家反转检验,可以使得连接两两地区的边为无向边。
步骤三:对n个地区进行两两距离比较,计算由地区距离长短决定的相异度矩阵,以此筛选对比地区的最佳组合。现较为主流的衡量两地区距离,即消费支出结构相似程度的指标为拉式、帕式指数之差PLS(Paasche-Laspeyres Spread)、加权对数二次方指标WLQ(the weighted log quadratic)和加权渐进二次方指标WAQ(the weighted asymptotically quadratic)[15]183-216,通过这些指标衡量地区间相似程度,计算公式如下:
ΔPLSjk(p1,p2,q1,q2)
(4)
ΔWLQ(p1,p2,q1,q2)
(5)
ΔWAQ(p1,p2,q1,q2)
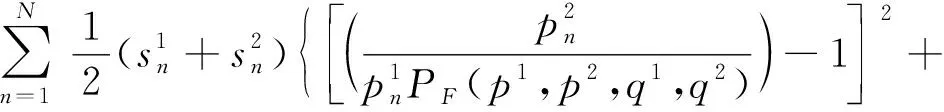
(6)
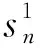
步骤四:最优路径求解,即根据上一步骤求得的地区间相异度矩阵,应用Dijkstra算法对任意两两地区间的最优路径问题进行求解,并借助MATLAB软件予以辅助计算,此时所求得的每一条路径中的直接邻国均倾向于具有相似的消费模式,这可以大幅提高比较的特征性,得到较可靠的双边比较结果。
步骤五:应用GEKS法对费暄指数进行修正,将其转化为满足传递性要求的购买力平价,GEKS调整公式表示为:
(7)
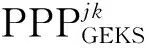
当直接运用GEKS法对地区或国家进行多边比较时,往往要求对比地区间的消费支出结构相差不大,否则结果将会造成较大偏差。故GEKS法更适用于对经济发展水平、消费规模、支出结构相近的国家进行比较。鉴于此,本文将最短距离法和GEKS法结合使用,即首先通过该方法来筛选得到对比国家或地区的最优组合,旨在将消费结构相似的地区进行直接比较,再通过GEKS法将双边比较结果链接成为多边比较,求解满足传递性的购买力平价结果。
(二)迪杰斯特拉(Dijkstra)算法
最短距离法的实现算法较多,目前较为经典的主要有4种,即:佛洛依德算法(Floyd)、贝尔曼-福特算法(Bellman-Ford)、队列优化算法(Shortest Path Faster Algorithm,简称SPFA)、迪杰斯特拉算法(Dijkstra),表1将对上述算法的适用范围等情况进行归纳和对比。

表1 最短距离算法适用情况对比
迪杰斯特拉算法(Dijkstra)是基于“贪心算法”原理且较为经典的单源最短距离算法,用于解决源点到所有结点最短距离计算的问题,且有着较高的运行效率,但该算法不能解决图中含有负权值的问题。在计算过程中,需要将每个参与比较地区作为基准地区来求解任意两两地区最优路径,而各地区购买力平价值均是相对基准地区而言,因此求解最短距离为单源问题,可通过Dijkstra算法实现。
Dijkstra算法以广度优先思想为核心,即定义某点为源点,将其作为中心向各目标结点层层扩展,直至扩展到终点为止。该算法将结点分成两部分,即未标记结点集和已标记结点集。对于某个赋权连通图G=(V,E),其中网络拓补图的顶点集合记为V,所有带权边的集合记为E。在该图中首先将源点归入已标记结点集S中,其他点则被归为未标记结点集U(S,U∈V)中,每次循环都是在未标记结点集中寻找距离源点路径长度最短的结点,并将其归入已标记节点集的过程,直至所有结点都成为集合S中的元素。在此过程中,总要保证从源点到集合S中各顶点的距离始终不大于到集合U中各顶点的距离。根据该过程可将算法描述为以下几个步骤[16]:
(1)将赋权连通图中的所有点间的距离存储于w邻接矩阵中,若两点不直接相连,即(vi,vj)不存在,则将w[i,j]记为。在初始状态下已标记点集合S仅有一个源点v0,未标记点集合U包括除源点外的其他顶点。设Dist[vo,j]为源点至其各点的最短距离,在初始状态下,Dist[v0,j]=w[v0,j]。
(2)在上一步求得的Dist[vo,j]中选择最小距离的顶点vj,即满足m_dist=min{Dist[v0,j]|j∈U},并将点vj加入集合S中,此时集合S=S∪{vj}。
(2015-北京-20) 已知数列{an} 满足:ai∈N*,a1≤36,且记集合M={an|n∈N*}.
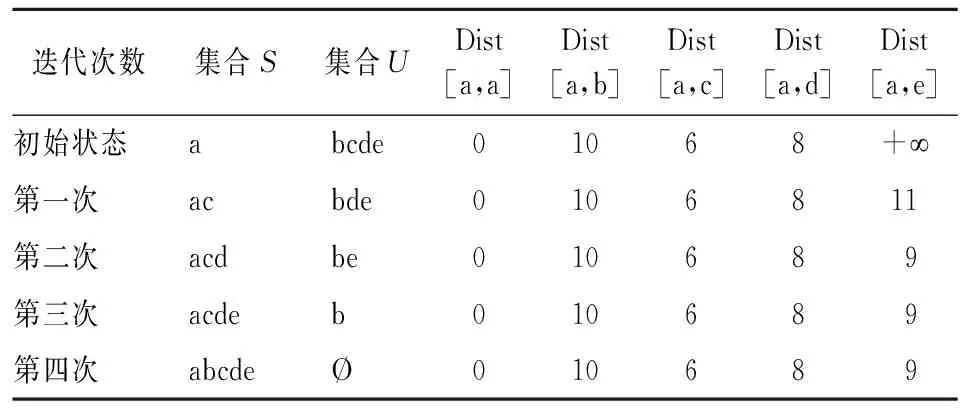
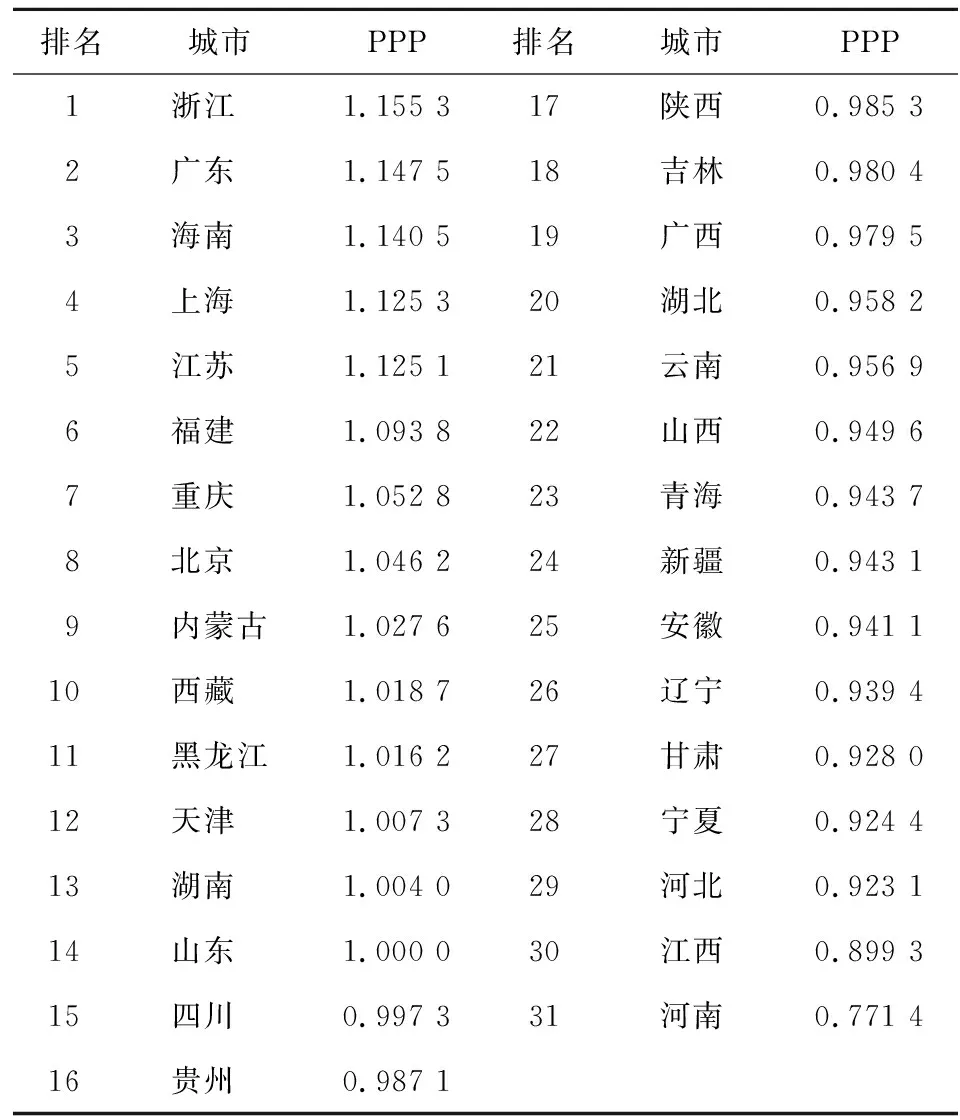
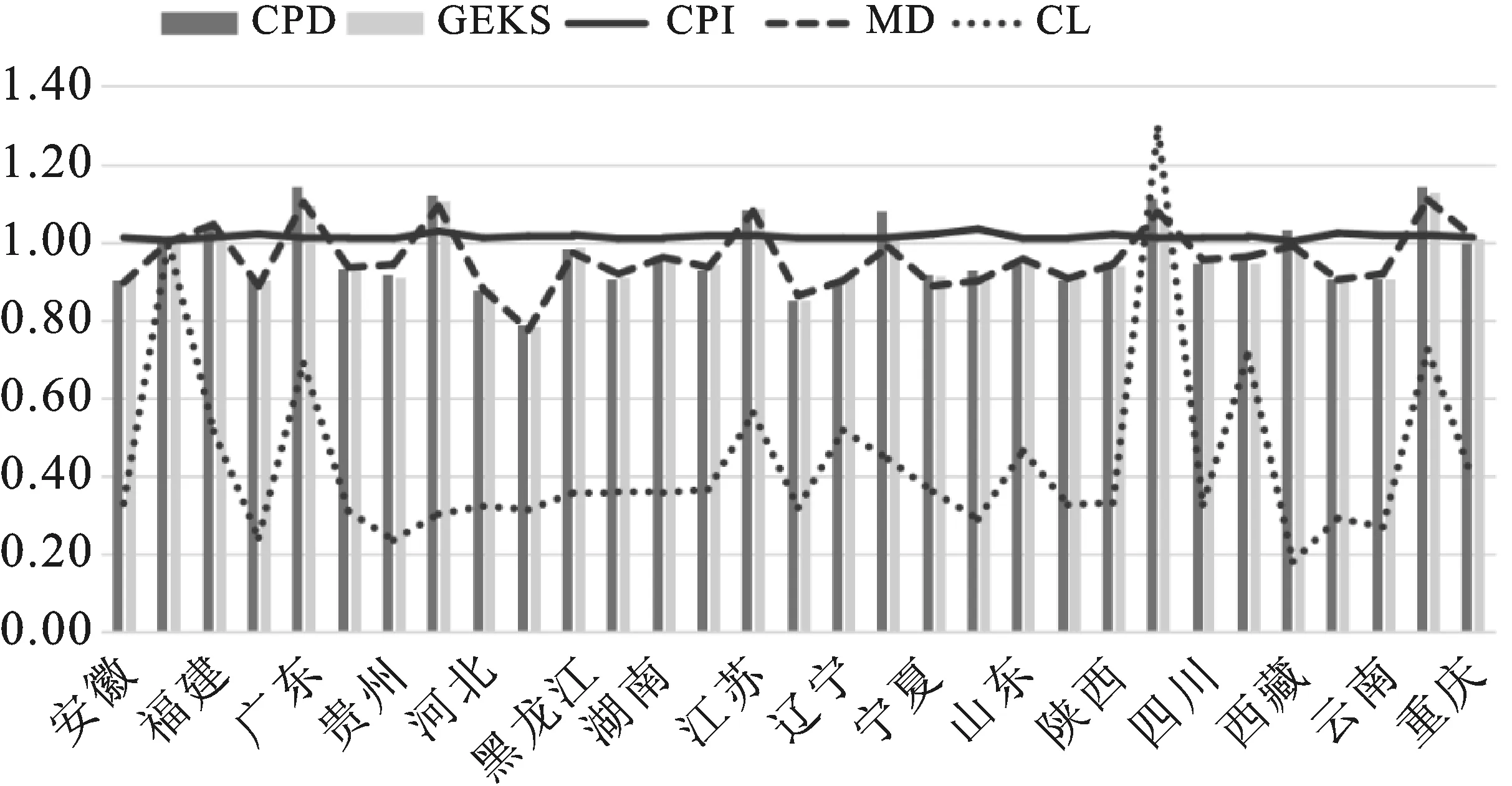
(3)对源点v0至各顶点的最短距离进行修改。若Dist[v0,j]+w[j,k] (4)重复步骤(2)和(3),直至集合S中包含图中全部顶点时,则算法终止,此时Dist[i,j]记录了从源点到其他各顶点的最短距离。 下面将通过一个例子来具体说明Dijkstra算法的基本步骤。对于图1,应用Dijkstra算法求得源点a至其他结点的最短路径,求解过程见表2。 图1 赋权无向图 在初始状态下,集合S中仅存在源点a,集合U中则包括其他未计算出最短距离的顶点集合,即b、c、d、e。另外,根据图中仅有e未与a点直接相连,故将源点a到e点的距离Dist[a,e]初始化为无穷大,而到其他源点的距离为其权重。在第一次迭代中,源点到各顶点的初始值中Dist[a,c]最小,因此将c点加入至集合S中,并寻找c点的邻居点a、d、e,观察其邻边权重。对于d点,由于Dist[c,d]为5,而Dist[a,c]+Dist[c,d]=11>Dist[a,d]=8,故Dist[a,d]仍保持原值。对于e点,由于Dist[c,e]为5,故可计算Dist[a,e]=Dist[a,c]+Dist[c,e]=11。在第二次迭代中,对比上一步所计算的源点至各顶点的距离,发现Dist[a,d]最小,故将d点加入至集合S中,对于e点,发现Dist[a,d]+Dist[d,e] 表2 Dijkstra算法求解步骤 1.最短距离法用于国家间比较的优点分析。(1)将特征最接近的地区进行直接比较。最短距离法致力于求解任意两两地区的最短路径,则每一条链接中的地区在经济特征、消费结构等方面均较为接近,这对于经济实力比较而言,是非常好的特征,可以最大限度地保证了对比地区间的同质可比性,由此所形成边的双边指数的可靠性达到最大,并可以得到较为准确的结果。(2)可预先对特定国家或地区可能存在的关联设定限制条件。基于最短距离法原理,通过对地区相异度指标值的改进,预先对特定地区间可能存在的关联设定限制条件,最大可能地得到与现实情况相符的比较路径。(3)受第三地区的影响较小。相比其他的多边比较方法,例如GEKS法和GK法,在对各国或地区进行多边比较时,需要所有参与地区的规格品价格和支出数据,其中一个地区的信息变动则会影响整体的比较结果。最短距离法的优点是,由于国家两两比较相对独立,比较结果受第三方的影响较小。(4)计算量显著降低。一旦依据相异度指标确定地区间的链接路径,即可将双边比较链接成为多边比较。相比其他的多边比较,该方法只需要让每个地区与邻近地区(消费结构、经济水平最相近的地区)进行比较,这大大减少了必须直接进行比较的地区数量,显著减少了计算量。 2.最短距离法用于国家间比较的缺点分析。(1)两两国情差异巨大使得链接路径基础较弱。最短距离法的核心是寻找结构相似(更具可比性)的经济体,需要对经济体进行两两比较,这需要两国的规格品价格数据和GDP多个层面的支出权重数据。由于国家之间的经济发展水平差距悬殊,在规格品选择上往往出现商品的可比性与代表性相互矛盾、选取的商品质量差距相差过大、各国消费结构相差较大使得权重难以设定等情况。而这些直接导致利用相关算法取得的最优路径的链式结构基础较弱,不利于得到客观合理的国际比较结果。这是最短距离法未在国际比较中得到推广的最大“桎梏”。(2)链接路径有可能不唯一。地区间的相似度权重互不相同时,通过最短距离法得到的链接路径是唯一的。但有两个甚至更多边的权重存在相同数值时,求得的最优化路径将不唯一。虽然在现实中,这类现象发生的频率并不大,但对结果有一定影响。 最短距离法用于国家间比较的优缺点,在国内购买力平价测度中有所变化。最显著的是有的缺点弱化,比如曾经的“桎梏”几近消失,同时,有的优点得到强化。 1.两两国情差异巨大使得链接路径基础较弱的缺点几近消失。相比国际购买力平价,国内购买力平价在测算难度上有所降低。虽然商品可比性与代表性存在矛盾、商品质量存在差距、消费支出权重难以设定,但由于一国内部统计制度一致、统计工作一致,使得上述问题不再是难题。甚至在采取相应的处理措施后,可以忽略不计。作为阻碍推广最短距离法在国家间比较使用的最大困难,几近消失,意味着该方法在国内购买力平价使用中的生命力有可能是较为顽强的。本文后续研究与现实的符合程度也说明了这一点。 2.可预先对特定国家或地区可能存在的关联设定限制条件得到强化。可预先对特定国家或地区可能存在的关联设定限制条件是最短距离法的一个优点。源于Hill的总结[11],即各国或各地区统计的数据质量参差不齐,最短距离法的控制措施是,使资源条件不足的国家尽量仅与一个国家具有双边关联的关系。这种“预先设定”的思想,在大国国内购买力平价测度中可以更好地使用。针对中国来说,存在经济发展程度、统计能力、经济结构、消费结构等差异很大的地区,比如北京和西藏,显然不应该出现二者链接在一起的结果,这时,可以用一个较大的虚拟值来代替K阶的PLS、WLQ、或WAQ矩阵中北京与西藏的相异度指标值,作为限定条件,使得结果更客观、科学。 测算国内购买力平价所需数据的收集主要涉及两方面:(1)各地区商品及服务价格的采集;(2)各地区基本类所占消费权重的确定。因此如何确定具有代表性和可比性的“商品篮子”,使其能够真实地反映居民的实际生活消费情况,是测算购买力平价的关键环节。 鉴于数据的保密性原则,单个规格品价格数据及部分支出权重数据,不可能获得较近年份的数据。目前从官方机构获得的最新数据为2010年商品或服务的价格数据及其权重信息(含31个省份)。为了保证数据的权威性,使得最终所测结果具有实际意义,本文选取的数据均来自官方的统计资料,包括部分公开出版的数据资料,主要来自《中国统计年鉴》《中国物价年鉴》《中国价格及城镇居民收支调查》、中国价格信息网、各地统计年鉴等。另外,由于中国尚未对国内购买力平价指数的编制有统一的官方说明,因此本文将重点着眼于测度方法优缺点的研究,旨在为相关机构提供方法方面的建议,而非规格品指标的选择。 由于中国目前尚未形成统一的国内购买力平价的编制方法,因此对于该问题的研究,笔者借鉴居民消费价格指数(Consumer Price Index,简称CPI)的分类方式。居民消费价格指数是根据居民日常所消费的篮子商品和服务项目的价格所计算的,衡量不同时期平均价格水平变动的相对数,是真实生活成本指数的一个近似指标。本文借鉴居民消费价格指数对商品及服务的分类方式,获得68种居民消费型商品和服务。覆盖8个基本类:食品、烟酒、衣着、家庭设备用品及维修服务、医疗保健、交通通信、教育文化娱乐服务、居住。 国内购买力平价的权重数据,理论上为GDP不同类别层面的支出权重,一般从GDP层面逐层向下细分,直至基本类。限于数据保密性,无法取得官方数据。限于人力,尚无可能收集数据。考虑到本文重点是考察测度方法,文章以居民消费价格指数的权重体系为基础进行调整。实际操作中发现,官方数据公布的各省份2010年家庭人均消费现金支出结构分为城镇和农村两个类别,部分文献处理方式为:仅将研究对象局限于城镇家庭。对于城镇人口小于50%的省份而言,这种做法有失偏颇。故本文综合考虑各省份城镇和农村的消费结构对总指数的影响,利用城镇人口占比对二者各类别商品的消费比重进行加权,得到最终权重结果。 本文使用最短距离法,测度了中国31个省份的货币购买力平价。本文主观地将山东省作为基准地区(PPP=1),分别以PLS、WLQ和WAQ作为衡量地区间相异度(相似度)的指标,求出的数值作为各地区“链式路径边”的权重,再利用Dijkstra算法得到任意两地区间的最优路径,由此求得最终结果。由于篇幅限制,本文仅列出以山东省为基准的最优路径,如表3所示,通过最短距离法测得的各省份购买力平价结果如表4所示。 表3 最短距离法最优路径 表4 国内购买力平价指数 如前所述,最短距离法最大的优点是通过将最为相似的地区链接求解PPP。为验证其效果,将主流的GEKS、CPD的结果与MD法进行比较,如图2所示。图中各省份按照拼音进行排序,GEKS、CPD、MD分别为基于各自方法得到的PPP值,CPI为各地区消费者价格指数,CL为各地区消费水平。 1.从PPP值来看,差异明显。从三种方法得到的PPP值来看,结果值无差异的有5个省份:河北、广西、北京、新疆、湖南。其余省份差异各有不同,差异最大的为内蒙古。另有5个省份因方法产生反向差异:上海、广东、西藏、吉林、四川。显然,这些差异主要由方法因素导致。 2.与CPI、消费水平相比较,MD法PPP值更接近现实。鉴于PPP选择山东为基准省份,值为1,CPI和消费水平也皆通过线性变换将山东处理为1,以使三者具有可比性。由图2可以看到,CPI值由于其计算方法和线性变换的影响,已游离于PPP值和消费水平曲线之外。与GEKS、CPD法相比,MD法PPP值走势与消费水平走势更为契合,由此认为其更接近现实。 图2 基于主流方法的PPP对比图 根据表4结果,整体来看各省份的购买力平价存在显著差异,说明等额货币所能购买到的商品或服务项目迥然不同。 1.省域视角的物价水平分析。具体来看,各省份的购买力平价值介于[0.771 4,1.155 3]之间,且最高值是最低值的1.498倍,其中价格水平最高的为浙江省,最低的是河南省。购买力平价最高的5名分别为浙江、广东、海南、上海、江苏,最低的5名分别为甘肃、宁夏、河北、江西、河南。通过计算31个省份的购买力平价指数的简单几何平均,来求得中国平均的价格水平,计算结果为0.996,基本和山东的价格水平持平,由此可证明选择山东省作为基准地区的正确性。另外,根据表中的数据结果,发现购买力平价大于1的省份共有13个,说明这些省份的物价水平均高于山东,且高于全国平均水平,但等金额的货币购买力却小于山东。通过观察,发现购买力平价指数高于山东的大多为经济发展水平较为发达的省份,且以沿海区域为主,具有代表性的为浙江、广东、上海、江苏、北京等,但不乏有经济水平欠发达的省份,比如西藏和内蒙古,这些省份由于自然条件的限制或较高的运输成本,使其物价水平挤入较高行列。另外,小于1的省份共有17个,这些省份的物价水平均低于山东省,且均低于全国平均水平,而等金额的货币购买力高于山东省和全国平均水平。这些地区多为经济欠发达省份,较具代表性的包括新疆、甘肃、宁夏、青海、河南。该现象说明某个省份的经济发展情况的确影响着该地的物价水平,但并非决定性因素,资源禀赋、地理位置等均成为影响因素。 2.八大综合经济区视角的物价水平分析。从区域角度来看,各区域价格水平差距较为显著。国务院发展研究中心也曾发表报告指出,中国所沿袭的“东-中-西”划分方法已不合时宜。故本文按照国家统计局经济区域划分方法,将中国划分为四大板块,并进一步将其划分为八大综合经济区[注]本文按照国家统计局经济区域划分方法,将中国划分为八大区域。其中,东北经济区包括辽宁、吉林、黑龙江;北部沿海经济区包括北京、天津、河北、山东;东部沿海综合经济区包括上海、江苏、浙江;南部沿海经济区包括福建、广东、海南;黄河中游经济区包括陕西、山西、河南、内蒙古;长江中游经济区包括湖北、湖南、江西、安徽;大西南经济区包括云南、贵州、四川、重庆、广西;大西北经济区包括甘肃、青海、宁夏、西藏、新疆。。 由箱线图(如图3所示)可知,各区域的购买力平价结果呈现“东部沿海经济区>南部沿海经济区>北部沿海经济区>大西南经济区>东北经济区>黄河中游经济区>长江中游经济区>大西北经济区”分布格局,即价格水平在空间上具有东高西低,依次递减的态势,其中价格水平排于前10名的省份中,有70%是东部地区,价格水平排于后10名的地区中,有80%是中西部地区。其中,沿海区域的平均购买力平价普遍高于其他区域,这3个经济区共同构成了传统划分方式的“东部区域”,是中国三大经济圈“长江三角洲”“珠江三角洲”以及“环渤海经济圈”的所在区域,是中国经济最为发达的地区,故价格水平相对较高,较符合预期。另外,在这3个经济区中,东部沿海、南部沿海经济区的平均物价水平最高,且远高于中国的其他经济区,离散程度相对较低,说明这两个区域中各省份的价格水平普遍较高。除了沿海区域外,其他经济区的购买力平价较为相近,大约为0.95。具体来看,其他区域各省份的国内购买力平价普遍较低,且除了内蒙古、湖南、重庆、西藏、黑龙江,其他省份的平均价格水平均低于山东。从离散角度来看,北部沿海经济区、黄河中游、长江中游区域内部省市的价格水平差距较大,其中黄河中游区域最为明显,其变异系数为0.121,是导致中国各省份间差距如此之大的主要原因。在该区域中,内蒙古的购买力平价最高,值为1.027 6,位于第9名,而等额货币所具有的购买力最高的省份为河南,购买力平价仅为0.771 4,是中国价格水平最低的省份。鉴于此,政府相关部门应给予重点关注,对各地区的物价水平予以宏观调控,从而降低中国区域间整体差距。 图3 各区域购买力平价箱线图 第一,在国际间购买力平价测度中使用受限的最短距离法,在国内购买力平价测度中,曾经的束缚几近消失,可以发挥极大优势。从本文的理论分析、数据结果与国家统计局课题组基于其他方法得到的结果较为接近则证实了这一点。 第二, 以往研究往往使用GDP支出权重,未对权重进行调整。本文认为城镇人口占比一定程度上反映了消费结构,用其对权重进行调整,使得结果更靠近客观现实。说明对权重进行调整,或许是构建国内购买力平价的有效途径。 第三,作为衡量地区相似度指标,WLQ和WAQ更优越,生成的链接路径更短,说明其中的双边比较地区的消费支出模式更为相似,特征性较强,且得到的链接路径更符合预期。PLS指标因只关注了比值,忽略了分子分母绝对值大小的影响,因此结果数据不总是正确。 第四,由最短距离法测算得到的购买力平价结果来看,各省份的价格水平存在显著差异,购买力平价值介于[0.771 4,1.155 3]之间,最高省份价格水平约为最低省份价格水平的1.5倍。排在前5名的地区为浙江、广东、海南、上海、江苏,最后5名分别为甘肃、宁夏、河北、江西、河南。从八大综合经济区角度看,价格水平整体呈现“东高西低”依次递减的态势,且沿海区域的价格水平显著高于内陆区域。北部沿海经济区、黄河中游、长江中游区域的差异较大,而黄河中游区域是造成中国价格水平差异较大的主要区域,政府等相关部门应给予一定的重视。 国际间购买力平价测度方法在国内应用时,存在诸多新情况,需要有针对性的研究。本文对最短距离法的研究侧重方法适用性分析、权重调整等。待改进的研究空间主要包括:1.基准地区选择对测度结果的本质影响;2.基本类层面国内购买力平价结果与客观事实的符合程度研究。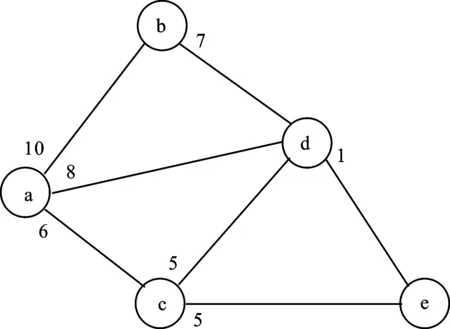
(三)最短距离法用于国家间比较的优缺点分析
(四)最短距离法用于国内地区间比较的新变化
三、数据说明及规格品选择
(一)数据说明
(二)规格品选取
(三)权重确定
四、实证结果及各省份物价水平分析
(一)国内购买力平价测度结果

(二)各主流方法PPP比较分析
(三)省域和八大经济综合区物价水平分析

五、主要结论与研究展望
(一)主要结论
(二)研究展望
