笼型无刷双馈电机稳态下转矩角的物理含义
2019-03-13白崟儒王淑红张爱玲刘昊青
白崟儒,王淑红,张爱玲,刘昊青
(太原理工大学 电气与动力工程学院,太原 030006)
相比于有刷双馈电机,无刷双馈电机省去了电刷和滑环,故其可靠性高、维护成本低,在风力发电等领域具有光明的应用前景[1-4]。无刷双馈电机的转子可采用笼型结构、磁阻式结构及混合式结构[5-9]。文献[10]指出笼型无刷双馈电机在稳态运行时的电磁转矩与功率绕组电流、控制绕组电流及转矩角(或称功角)正弦值三者的乘积成正比,在文献[11]中,具有相同的结论,但现有文献均未能清楚地说明转矩角的物理含义,也未能给出转矩角的简洁计算公式。无刷双馈电机内部含有两个极数不同的磁场,其内部磁场异常复杂,如果能清晰地阐明转矩角的物理含义,则有助于更深入地理解无刷双馈电机稳态工作时的内部能量转换机理,进而为无刷双馈电机的研究、技术改进提供一定程度的理论依据。同时,获得转矩角的计算公式也有助于简化无刷双馈电机稳态仿真过程。
本文从笼型无刷双馈电机的内部磁场角度入手,推导无刷双馈电机在稳态电磁转矩的解析表达式,进而获得转矩角的表达式,在此基础上分析转矩角的物理含义,最后分析结果被有限元仿真所验证。
1 推导
为了简化推导过程,假设:
1) 不考虑各部件的剩磁、饱和、磁滞和涡流效应;
2) 定子绕组电流产生的气隙磁场在空间中按正弦分布;
3) 不计定、转子表面齿、槽的影响;
4) 忽略转子电阻;
5) 转子同心多环单元被简化为单环单元,如图1所示。
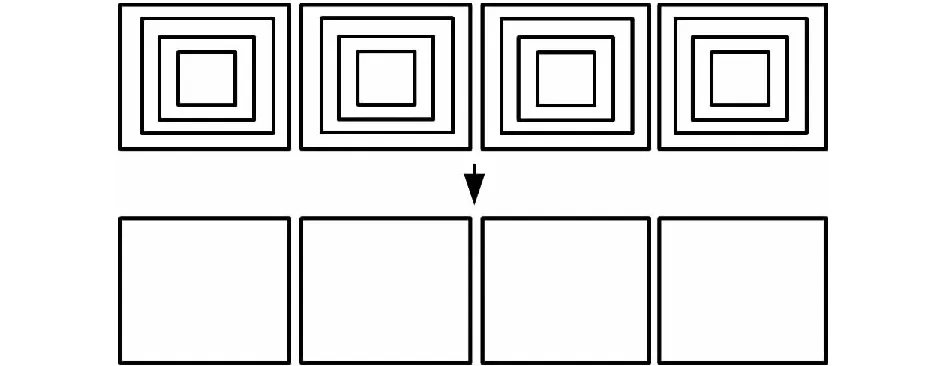
图1 转子导条的简化Fig.1 Simplification of rotor winding
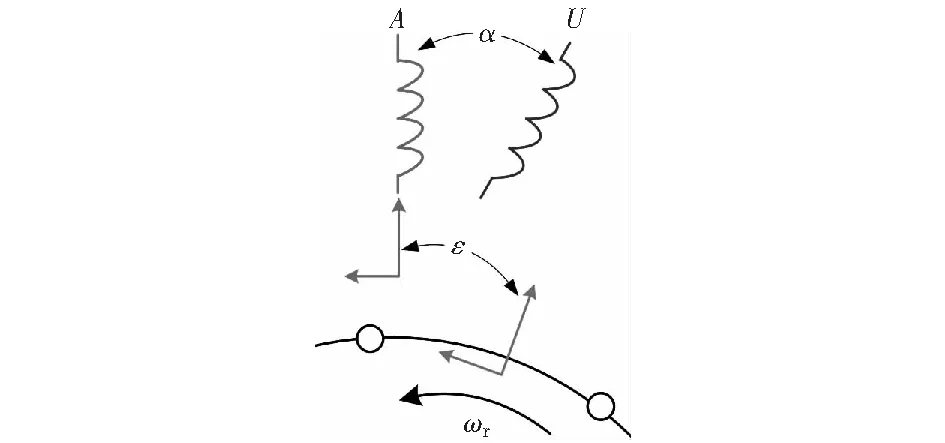
图2 t=0时定、转子参考系的位置关系Fig.2 Position relation between the stator and rotor reference frame when t=0
所研究的无刷双馈电机的定子含有A,B,C三相功率绕组和U,V,W三相控制绕组。设定子参考系的坐标原点位于功率绕组A相轴线上,功率绕组与控制绕组轴线之间的角度差为(机械角度)α;转子参考系的坐标原点位于第一个线圈组的中心线上(轴线),由于在稳态状态下,转子以角速度ωr转动,因此定子坐标轴与转子坐标轴之间的相对位置在不断变化,设0时刻的时候,定子参考系的坐标原点超前转子参考系的角度为ε.图2显示了该假设条件下定、转子参考系的位置关系。设笼型无刷双馈电机在稳态状态下功率绕组电流为
(1)
设笼型无刷双馈电机在稳态状态下亚同步状态时控制绕组电流为
(2)
设笼型无刷双馈电机在稳态状态下超同步状态时控制绕组电流为
(3)
式中:γ与β是各自电流在0时刻下的初始相位角;IspM和IscM是各自电流的幅值;ωp和ωc是各自电流的角频率。在定子坐标系下,功率绕组电流产生的磁密为
(4)
在亚同步状态下,定子坐标系下的控制绕组电流产生的磁密为
(5)
在超同步状态下,定子坐标系下的控制绕组电流产生的磁密为
(6)
式中:pp是功率绕组极对数;pc是控制绕组极对数;BspM是功率绕组电流所产生的磁密的幅值;BscM是控制绕组电流所产生的磁密的幅值;θ0是在定子坐标系下的位置坐标。转化为转子坐标系时,定子绕组不再静止,而是以-ωr的速度旋转,则容易得知
θ0=θ+ωrt-ε.
(7)
式中,θ是在转子坐标系下的位置坐标。将式(7)代入式(4)可以得到转子坐标系下功率绕组电流产生的磁密为
bsp=BspMcos[ωt+γ-pp(θ-ε)] .
(8)
将式(7)代入式(5)和式(6),并将亚同步和超同步的公式形式统一化,则在转子坐标系下控制绕组电流所产生的磁密为
bsc=BscMcos[ωt+(-1)j·β+pcα+pc(θ-ε)] .
(9)
式中:当电机处于亚同步状态时,有ω=ωp-ppωr=ωc+pcωr且j=2;当电机处于超同步状态时有ω=ωp-ppωr=pcωr-ωc且j=1.对于第k个转子回路,其所铰链的定子磁通为
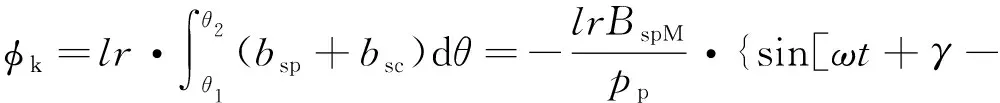
sin[ωt+(-1)j·β+pcα+pc(θ1-ε)]} .
(10)
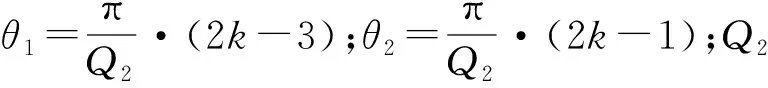
(11)
在忽略了转子电阻的假设条件下,每个转子短路环中所铰链的转子电流磁通与定子电流磁通必然大小相等,方向相反。同时考虑到转子短路环电流产生的都是矩形磁场,故在转子坐标系下第k个转子短路环所在位置处的转子电流所生成的磁密为
(12)
将式(12)傅里叶分解,其中pp对极磁场分量为
(13)
由式(13)可见,转子电流所生成的pp对极磁场分量包含两部分,前一部分由功率绕组电流激励产生,且与定子电流所生成的pp对极磁场完全反向,因此这一部分不产生电磁转矩;后一部分由控制绕组电流激励产生,且与定子电流所生成的pp对极磁场的空间夹角(以电角度计)为
γ-(-1)j·β-pcα+(pc+pp)ε+π .
因此这一部分将与定子电流所产生的pp对极磁场互相耦合产生电磁转矩。
将式(12)傅里叶分解,其中pc对极磁场分量为
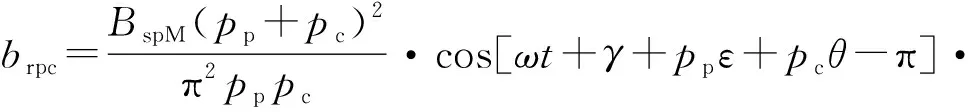
(14)
由式(14)可见,转子电流所生成的pc对极磁场分量同样也包含两部分,后一部分由控制绕组电流激励产生,且与定子电流所产生的pc对极磁场完全反向,因此这一部分不产生转矩;前一部分由功率绕组电流激励产生,且与定子电流所产生的pc对极磁场的空间夹角(以电角度计)为
γ-(-1)j·β-pcα+(pc+pp)ε+π .
因此这一部分将与定子电流所产生的pc对极磁场互相耦合产生电磁转矩。由电机理论,可以进一步推导得到无刷双馈电机的电磁功率(限于篇幅,此处省略推导过程)
(15)
式中:Lpm是定子功率绕组的激磁电感,φ=γ-(-1)j·β-pcα+(pc+pp)ε+π.由上述推导可知,转矩角φ的计算表达式为
φ=γ-(-1)j·β-pcα+(pc+pp)ε+π .
(16)
式(16)有助于在无刷双馈电机稳态有限元仿真中快速、方便地确定的转矩角数值、及调整转矩角,解决了无刷双馈电机稳态有限元仿真中转矩角计算繁杂的问题。
2 转矩角的物理意义
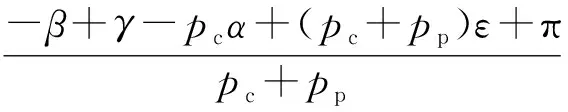
(17)
(18)
为方便,称该位置为定子磁场反相点,由此可知转矩角的物理意义:转子坐标系中定子磁场反相点与转子导体回路中心线之间的机械夹角与pc+pp的乘积。如果BspM=BscM,则定子磁场反相点的振幅总是零,这类似于驻波的波节;但如果BspM≠BscM,则定子磁场反相点的振幅不为零。设θ'是定子磁场反相点的坐标,即
cos[ωt+γ-pp(θ'-ε)]=-cos[ωt+(-1)j·β+pcα+pc(θ'-ε)] .
(19)
易知
ωt+γ-pp(θ'-ε)-(2m-1)π=ωt+(-1)j·β+pcα+pc(θ'-ε) .
(20)
可以得到
(21)
式中,m=1,2,3…。由式(21)可见,当1≤m≤pc+pp时θ'<2π;当m>pc+pp时,θ'>2π。因此,在气隙一个完整圆周内,共有pc+pp个定子磁场反相点,这与转子导体回路中心线的数量相等。由于上述式子都是在转子坐标系中得到的,因此当无刷双馈电机运行在稳态时,定子磁场反相点与转子保持同速旋转,转矩角保持不变。当无刷双馈电机处于电动稳态运行状态时,如负载转矩突然增加,则会拉动转子使得转子导体回路中心线与定子磁场反相点之间的夹角增大,即转矩角增大,因而电磁转矩相应增大,从而重新与负载转矩相平衡,电机继续保持原转速运行。由此可见,定子磁场反相点可以看作是同步电机定子磁场的轴线,转子导体回路中心线可以看作是同步电机转子磁场的轴线,则无刷双馈电机的运行特性与一台pc+pp对极同步电机相同。
3 有限元仿真验证
使用有限元仿真软件验证上述分析的正确性。图3显示了有限元模型。该模型定子功率绕组为2对极,控制绕组为4对极;当无刷双馈电机稳态运行时,气隙磁场由定子磁场与转子磁场合成,故难以通过气隙磁密值确定定子磁场反相点。因此,本文采用如下仿真方案来验证理论分析的正确性:

图3 笼型无刷双馈电机的有限元模型Fig.3 Finite element model of a cage brushless double-fed machine
1) 在有限元仿真软件中,分别建立笼型无刷双馈电机模型a与模型b。模型a与模型b的各项参数都相同,区别仅在于模型b的转子导条开路,而模型a的转子导条正常闭合;
2) 给模型a的定子功率绕组和控制绕组施加电流源,转子固定转速旋转,转子转速与定子功率电流、控制电流频率满足双馈运行的约束条件,进行有限元仿真;给模型b施加完全相同的仿真设置进行仿真;
3) 由模型b的仿真结果可以确定气隙中定子磁场反相点的位置,以及定子磁场反相点到与之相邻的转子回路中心线之间的机械角度,从而确定转矩角;由模型a的仿真结果确定与该转矩角所对应的电磁功率;
4) 改变转矩角,得到电磁功率随转矩角变化的曲线。
表1分别显示了不同时刻定子磁场反相点在定子坐标下、转子坐标系下的坐标,以及磁密值的有限元仿真结果。为了突出定子磁场反相点,特设置BspM≈BscM.由表1可见,定子磁场反相点始终与转子保持同速旋转,则易知其与转子导体回路中心线之间保持相对静止。图4显示了转子坐标系下不同时刻定子磁场在气隙中的分布,图中红色、蓝色和黑色线条分别标记了0.005 s时刻、0.01 s时刻和0.013 5 s时刻定子磁场在气隙不同位置处的分布,该图的横坐标为转子坐标系下的位置坐标。在图中黑点标记位置,三条曲线的数值几乎都为零,易知图中黑点就是定子磁场反相点位置,由图可见共有6个磁场反相点,这与理论分析结果一致。图5 显示了定子磁场反相点和转子导体回路中心线之间的电角度夹角取不同值时无刷双馈电机的电磁转矩数值,可见电磁转矩与该角成正弦变化,这表明定子磁场反相点和转子导体回路中心线之间的电夹角就是无刷双馈电机的转矩角。

表1 不同时刻定子磁场反相点的坐标及磁密值Table 1 Coordinates and magnetic density values of the inverse phase of stator magnetic field at different time
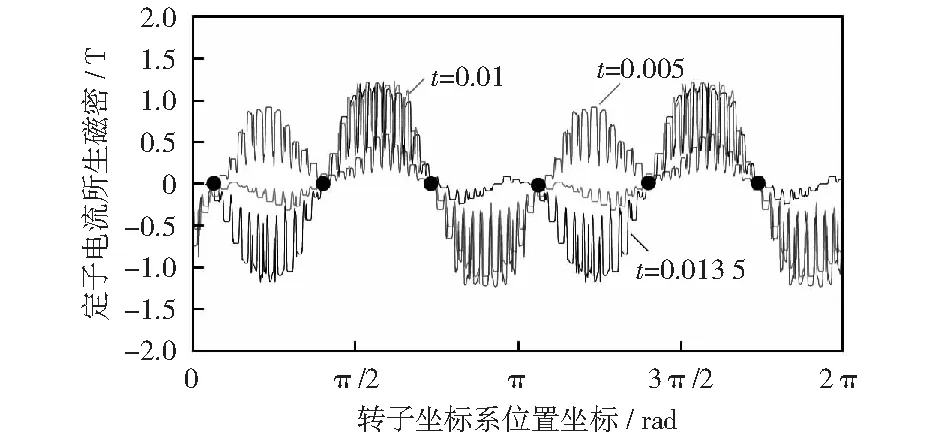
图4 转子坐标系下不同时刻定子磁场在气隙中的分布Fig.4 Distribution of stator magnetic field in air gap at different time in rotor coordinate system

图5 定子磁场反相点和转子导体回路中心线之间的电角度 夹角取不同值时无刷双馈电机的电磁转矩数值Fig.5 Electromagnetic torque value of brushless doubly-fed motor when the Angle of electric Angle between stator magnetic field reverse-phase point and rotor conductor circuit center line is different
4 结束语
本文从笼型无刷双馈电机的内部磁场角度入手,推导了无刷双馈电机在稳态运行时电磁转矩的解析表达式,获得了转矩角的计算公式,并揭示了转矩角的物理含义。理论分析及有限元仿真结果表明:笼型无刷双馈电机的转矩角是转子磁场与定子磁场的空间夹角,同时也是定子磁场反相点与转子导体回路中心线之间的机械角度与pc+pp的乘积;在机械角度一个完整圆周内,共有pc+pp个定子磁场反相点,当无刷双馈电机运行在稳态时,定子磁场反相点与转子保持同速旋转、相对静止;稳态运行时,定子磁场反相点可以看作是同步电机定子磁场的轴线,转子导体回路中心线可以看作是同步电机转子磁场的轴线。本文的研究结果为更深入地理解无刷双馈电机稳态工作时的内部能量转换机理提供了一定的帮助,也有助于简化笼型无刷双馈电机稳态仿真过程。
