小型运动体高速倾斜入水空泡流动数值研究
2019-03-13陈晨魏英杰王聪
陈晨, 魏英杰, 王聪
(哈尔滨工业大学 航天学院, 黑龙江 哈尔滨 150001)
0 引言
入水过程是指运动体以一定的初始速度从空气中穿越自由液面进入水中的过程。尤其对于高速运动的运动体,这一过程中伴随着湍动、相变、介质突变等非常复杂的流动过程,具有强烈的非定常性和瞬时性,对于运动体的运动特性、流体动力特性及流场结构等影响非常大。
对于入水问题的研究自19世纪末[1]以来取得了大量研究成果,早期研究多为球体低速垂直入水各阶段的入水现象研究。之后的研究开始转向如空气压强、空气密度等环境因素[2],以及球体密度、表面粗糙度和尺度等结构因素[3-5],对入水空泡的发展演化以及动力特性等影响分析。Shi等[6-7]应用光学观察技术及步枪进行了一系列子弹垂直入水实验,得到了入水喷溅、回射流及空泡流等非定常流动特性,同时发现子弹入水后的弹道偏移与入水深度有关。为研究入水弹道偏转问题,Truscott[8]开展了不同形状子弹的小角度倾斜入水实验,结果表明大长细比、钝头的模型能较为稳定地在水中运动。王云等[9]采用入水实验方法对不同头型的弹体进行了弹道研究,结果表明入水角对入水弹道的偏移影响较大。实验方法在对入水问题的研究中起到了重要作用,它可以直观地反映出运动体在入水过程中的空泡演化及弹道等,然而更深入的空泡流场动力特性以及流场结构则需要通过数值方法来实现。Erfanian等[10]采用耦合的欧拉- 拉格朗日(CEL)方法分别对球体和半球头射弹模型进行了数值模拟,得到的空泡轮廓及弹道与实验结果[10]和文献[11]吻合较好。为研究锥头圆柱体高速入水所产生的空泡深闭合现象以及周围流场结构,马庆鹏等[12]通过求解雷诺时均(RANS)方程对深闭合过程进行了数值模拟,发现高压区均在分离点附近。李永利等[13]应用CFX软件对航行器入水跳弹过程进行了数值计算,总结了易发生跳弹现象的航行器结构特征。孙钊等[14-15]基于流体体积(VOF)法多相流模型对具有不同表面润湿性的球体入水空泡开展了数值模拟研究,当球体表面为半疏水- 半亲水时将产生“心”型喷溅,且入水轨迹向亲水一侧偏斜,同时给出了形成不同入水空泡形态的临界速度与表面接触角的预测公式。胡明勇等[16]应用LS-DYNA软件对射弹垂直入水过程进行了流体与固体耦合数值计算,结果表明射弹头部受到的应力最大,且当头部圆台完全入水后阻力系数趋于定值。Valdi等[17]对立方体、圆柱体、球体、角锥体及圆椎体入水过程分别开展了数值模拟,研究表明立方体受到的阻力最大,而圆锥体所受阻力最小。
近年来一些学者将关注点转移到运动模型、进入液体及入水方向等。Jiang等[18-19]使用射钉枪将射弹打入不同浓度十六烷基三甲基氯化铵(CTAC)溶液中以及水中进行实验,同时开展数值模拟,研究发现相对于进入水中,射弹在减阻溶液中的空泡较大且阻力系数较小。王瑞琦等[20]对细长体水下运动的弹道及压力波进行了水平入水实验与数值模拟研究,研究发现细长体可以在空泡中平稳运动,压力波在射弹进入水中即开始形成,同时压力达到最大值。Hurd等[21]对弹性球体入水问题进行了研究,结果表明在球体后方存在嵌套空泡,且弹性球体的变形和振动与球体材质及撞击条件有关。
目前研究较多的是运动体低速垂直入水问题,而对于高速倾斜入水问题因其自身的复杂性以及对实验和数值计算的要求较高等原因,现有的研究成果较少。而垂直入水作为对研究入水问题的简化已无法满足实际应用的需求,现实中的射弹和空投鱼雷入水时均与自由液面呈一定的角度,即使是垂直发射,在实际海况的影响下也会倾斜入水。因此开展运动体高速倾斜入水问题的研究是非常必要的。
本文采用三维面对称模型并基于RANS方程建立小型运动体高速倾斜入水数值计算方法,并应用实验结果对数值方法进行验证,在此基础上对入水过程多相流场特性进行进一步分析,并研究入水角度对入水流场的影响。
1 数值方法
1.1 控制方程
Lee[22-23]指出:当入水速度小于700 m/s时可以忽略水的可压缩性;另外为简化计算,假设空气为不可压缩流体,同时忽略热效应。
小型运动体高速倾斜入水问题涉及气相、汽相、液相三相流动问题,本文将选取VOF多相流模型进行描述。
混合介质的连续性方程为
(1)
动量守恒方程为
(2)
式中:ρm为混合密度,ρmρvαvρgαgρlαvαg,ρv、ρg、ρl分别表示水蒸气密度、空气密度、水密度,αv、αg、αl分别表示水蒸汽体积分数、空气体积分数、水体积分数;ui、uj为平面笛卡尔坐标系下的速度分量,μv、μg、μl分别为水蒸汽动力黏度、空气动力黏度、水动力黏度;p为压力;μmμvαvμgαgμlαvαg为混合介质的动力黏度;μt为湍动黏度;xi、xj为平面笛卡尔坐标系下的位移分量;t为运动时间。
本文选取SSTk-ω湍流模型用于计算,其表达式为
(3)
(4)
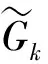
当运动体在高速运动时会引起空化现象,因此本文选取Zwart-Gerber-Belamri模型来描述水相与水蒸汽相之间的质量传输,其表达式为

(5)
式中:RB为气核半径;αnuc为汽化核心体积分数;Fvap为汽化系数;Fcond为凝结系数;pv为饱和蒸汽压力。
1.2 计算模型与边界条件
计算模型选用与实验一致的刚制实心回转体结构,如图1所示。模型头部为平头空化器,空化器直径d=2.2 mm,锥台半锥角θ=8°,柱段直径D=6 mm,模型总长L=48 mm,质量为8.5 g.
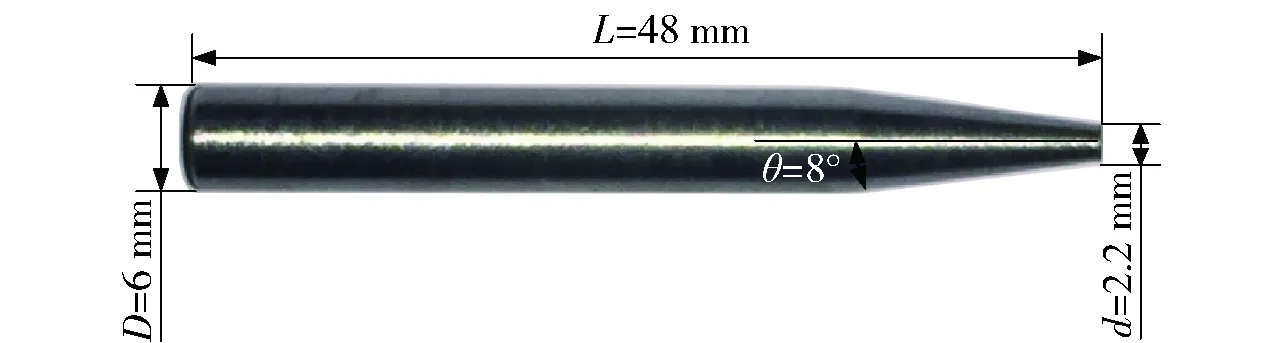
图1 计算模型Fig.1 Computational model
图2为计算域示意图,其中计算域为半圆柱体,入水角β为运动体轴线与自由液面的夹角,弹体头部中点距离自由液面高度为4D,流场空气域高度为95D,水域深度为65D,流场直径230D. 本文采用动计算域网格方式[24]实现运动体的3自由度运动,采用该方式在提高计算效率的同时也减小了网格更新过程中引起的计算误差。
为便于后续的结果分析,现对时间坐标系与空间坐标系进行定义,如图3所示。时间零点选在模型头部中点与自由液面接触时刻,因此入水前时间表示为负值,入水后时间为正值。空间坐标系中的模型局部坐标系O′sR的原点O′选在头部中点,s轴沿模型轴线,R轴垂直于s轴。空间全局坐标系Oxy的坐标原点O取为模型头部中点与自由液面交点,即入水撞击点。x轴正方向为重力方向,y轴为水平方向。
1.3 网格与计算模型的选取
当运动体高速入水时,运动体附近存在气相、汽相、液相3种流体,因此运动体附近的网格划分十分重要。首先建立3种不同网格密度的网格,网格数量分别为:250.83万(网格密度-1)、186.36万(网格密度-2)及93.23万(网格密度-3)。经计算得到如图4所示的运动速度v随时间t变化曲线。由图4可知,随着网格密度的增加,不同密度的网格计算所得速度之间差异逐渐减小。已知相同时刻实验得到的运动速度略大于数值计算结果,且综合考虑计算的准确性以及所需计算时间等问题后,最终选取网格密度-1的网格用于本文计算。
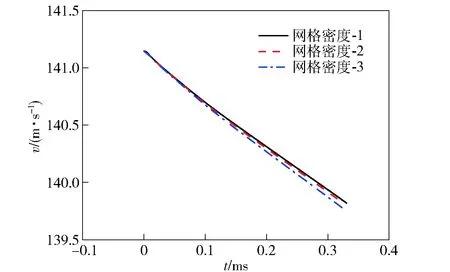
图4 不同网格密度的计算结果Fig.4 Calculated results of different mesh densities
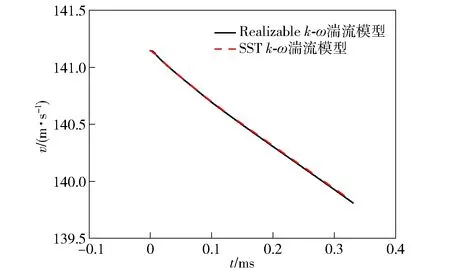
图5 不同湍流模型的计算结果Fig.5 Calculated results of different turbulence models
马庆鹏[25]在对运动体高速垂直入水多相流场特性进行研究时发现,应用Realizablek-ε模型和SSTk-ω模型能较好地模拟高速入水过程。因此,本文分别选择Realizablek-ε和SSTk-ω两个湍流模型用于计算,对比结果如图5所示。由图5可知,两种湍流模型所得计算结果差别很小,相比之下SSTk-ω模型能更为准确地预测壁面流动分离问题,因此本文选取SSTk-ω模型对RANS方程提供湍流封闭。
在确定了网格密度及湍流模型之后,分别针对Schnerr-Sauer空化模型和Zward-Gerber-Belamri空化模型进行计算,对比结果如图6所示。从图6中可以看出,应用不同空化模型计算所得结果基本一致,同时参考文献[25],最终选择Zward-Gerber-Belamri空化模型用于计算。
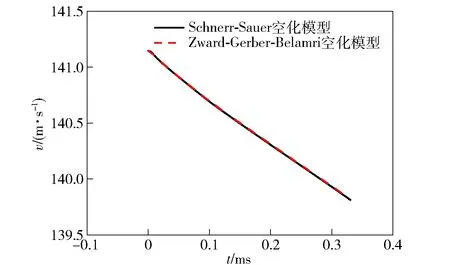
图6 不同空化模型的计算结果Fig.6 Calculated results of different cavitation model
1.4 数值方法验证
为验证本文数值方法的正确性和适用性,用小型运动体高速倾斜入水实验结果与本文数值计算结果进行对比验证。
图7为实验装置示意图,主要由轻气炮、水箱、照明灯组、高速摄像机以及电脑组成。实验模型如图1所示。运动体初始入水角度为43.6°,初始入水速度为141.15 m/s.
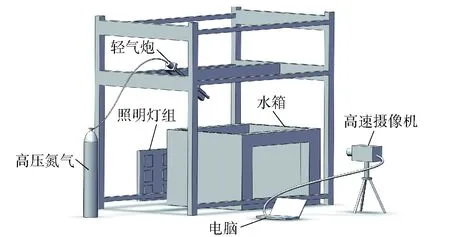
图7 实验装置示意图Fig.7 Schematic diagram of experimental setups
图8为运动体运动速度随时间变化的对比图,其中v0为初始入水速度。由于运动体在空气中运动时受到的阻力较水中的阻力小得多,在运动体接触水面后速度迅速衰减。从图8中可以看出,数值模拟得到的结果与实验结果变化趋势一致,数值模拟的运动速度衰减稍快于实验结果,速度误差为0.9%.

图8 运动速度对比Fig.8 Comparison of velocities
图9为模型入水后的姿态角随时间变化对比图。从图9中可以看出:二者结果趋势一致,在入水初期运动体在流体动力及重力作用下发生了偏转;随着入水深度的增加,模型继续偏转,姿态角逐渐变小直至模型触碰到空泡壁,后又反弹回空泡内。对于姿态角,数值模拟结果与实验结果的误差仅为0.2%.
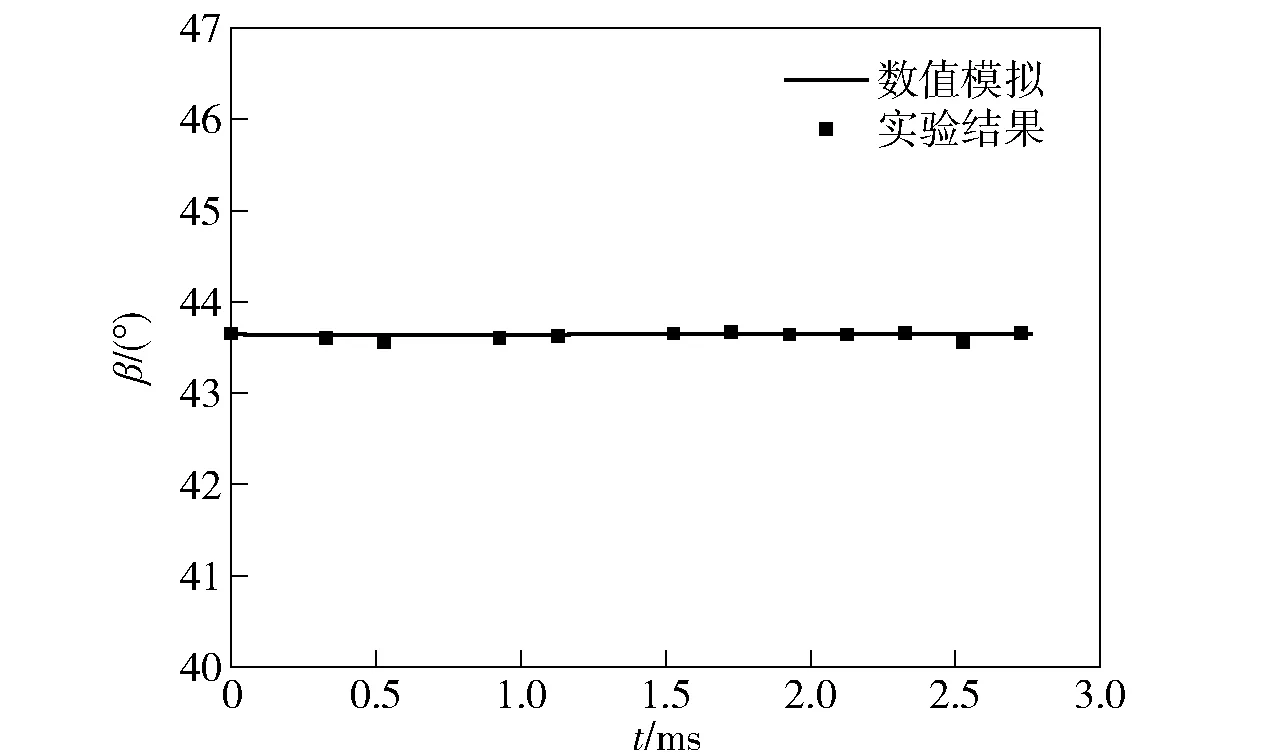
图9 入水姿态角对比Fig.9 Comparison of attitude angles
图10为空泡尺寸对比图,其中Lc为空泡长度,
Dc为空泡直径。数据测量方法如图11所示,其中Dc测量位置为Lc中点处。由图10可以看出,数值方法对于空泡轮廓的模拟较好,包括空泡长度与直径,与实验得到的空泡尺寸吻合度较好。分别选取实验和数值模拟在入水后0.33~2.73 ms的入水空泡形态进行对比,结果如图12所示。从图12中可以看出,数值模拟的水面喷溅现象不够明显,但就入水各阶段而言,数值模拟得到了从入水初期的空泡敞开阶段到空泡发生闭合的各种现象,与实验结果吻合较好。
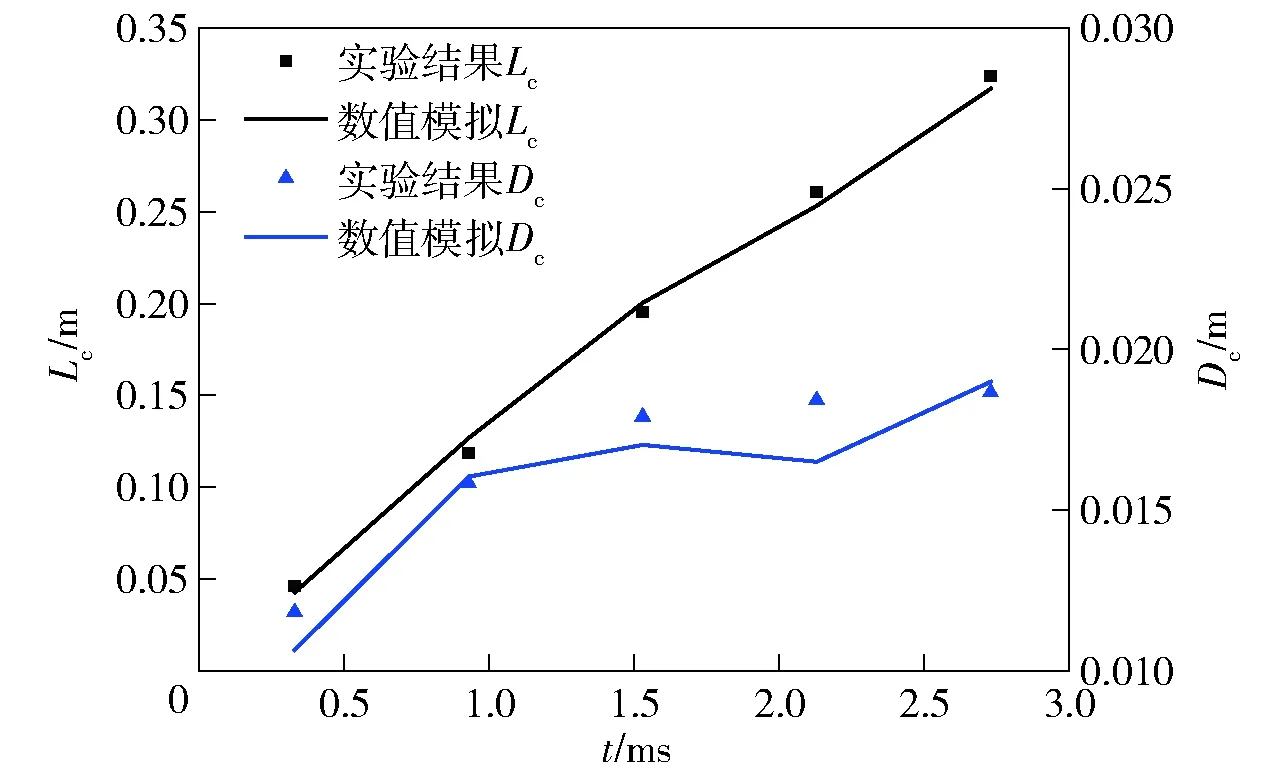
图10 空泡尺寸对比Fig.10 Comparison of cavity sizes
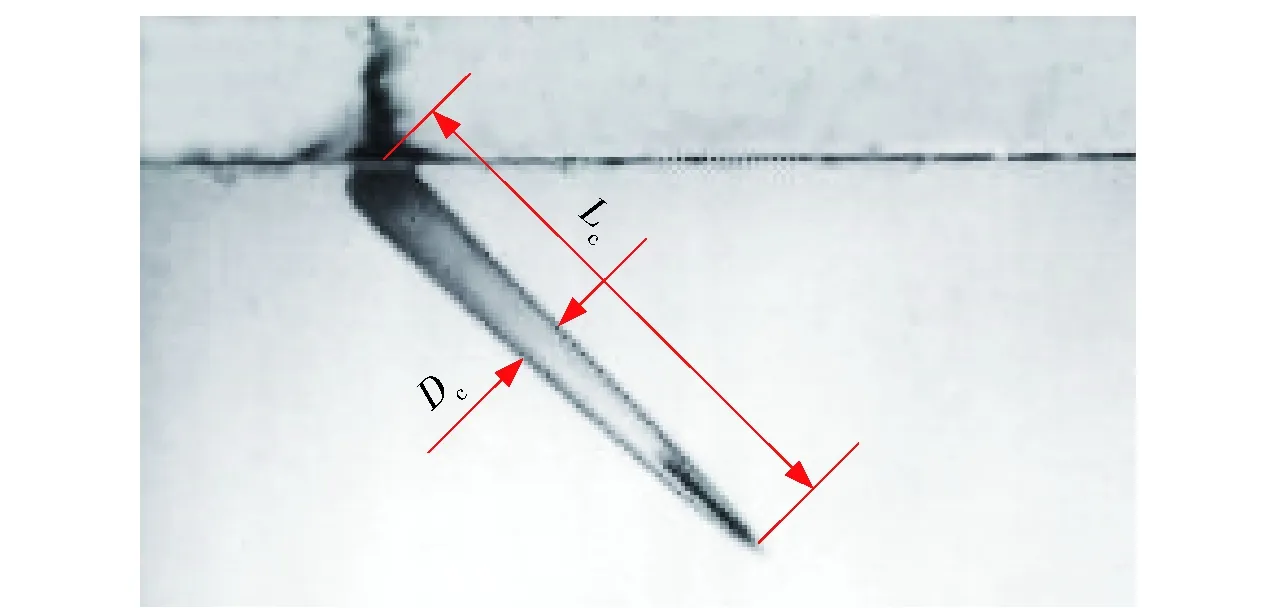
图11 测量方法示意图Fig.11 Parameters measured from photographic data
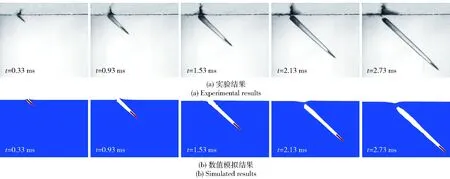
图12 空泡形态对比Fig.12 Comparison of cavity shapes
通过上述对比可知,数值模拟结果与实验结果吻合较好,因此可以认为本文数值方法适用于对高速运动体倾斜入水多相流场特性的研究。
2 结果与分析
2.1 入水过程流体动力特性分析
分析流体动力特性一般常用的参数有阻力系数Cd、升力系数Cl以及俯仰力矩系数Cm,它们的表达式分别为
(6)
(7)
(8)
式中:Fd为阻力;Fl为升力;M为俯仰力矩;A0为特征面积。
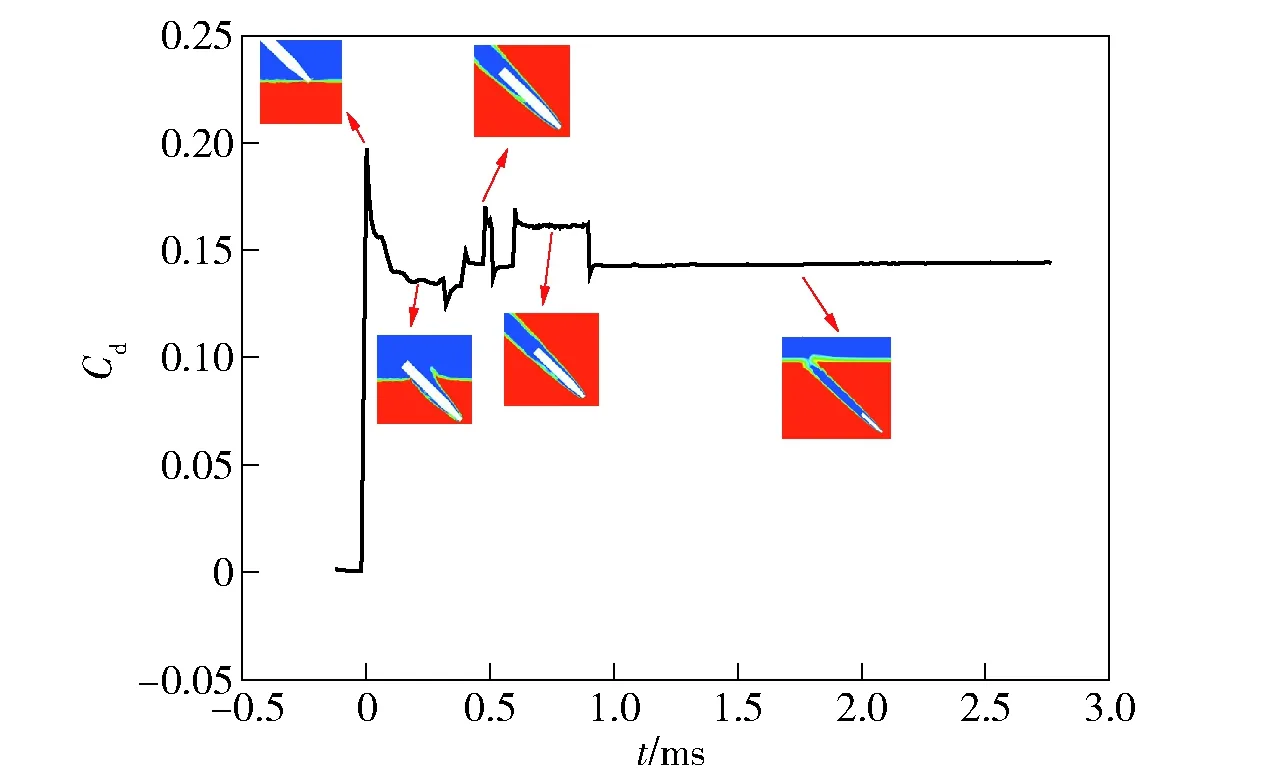
图13 阻力系数随时间变化Fig.13 Drag coefficient versus time
图13为阻力系数随时间变化曲线。由图13可知,在运动体入水之前阻力系数很小,在触水瞬间迅速达到一个峰值,这是因为空气密度比水的密度小得多,运动体在空气中受到的阻力也相对较小,但当运动体头部接触水面后其所受阻力在极短时间内急速增大,之后空泡逐渐形成,运动体由于空泡的包裹而使阻力减小。在0.25~1.0 ms范围内,阻力系数发生了波动,这是因为运动体的姿态角发生了变化,使运动体接触到空泡壁,运动体的沾湿面积不断变化,导致阻力系数不断波动。运动体与空泡相互作用示意图如图14所示。由图14可见,当运动体姿态发生变化而碰触空泡壁时,空泡会给运动体一个向上的反作用力F,而F可分解为垂直于运动体纵轴的升力Fl和与纵轴平行的阻力Fd,同时当溅起的液滴使运动表面沾湿时也会增加运动体的摩擦阻力,因此运动体姿态变化影响了阻力系数的波动。但随着尾拍现象的发生,运动体最终返回至空泡内,达到一个稳定的带空泡运动状态,此时阻力系数也趋于平稳。

图14 运动体与空泡相互作用示意图Fig.14 Schematic diagram of interaction between model and cavity
运动体入水过程中的升力系数变化如图15所示。由图15可见,运动体在入水撞击阶段头部与水接触,此时流体给了头部一个较大的反作用力,因此升力系数在入水初期有一个峰值。随着入水的深入,运动体沾湿区减少,升力系数迅速减小,最后达到一个稳定状态。在空泡形成后,由于运动体的攻角几乎为0°,升力系数相比阻力系数要小得多。尽管升力在运动体入水撞击阶段的数值较大,但升力对运动体的作用时间十分短暂,之后由于运动体运动时的攻角几乎为0°,也几乎不存在升力,且入水撞击阶段升力的作用可以在力矩系数中体现。因此,本文后续研究不再单独对升力系数进行分析。
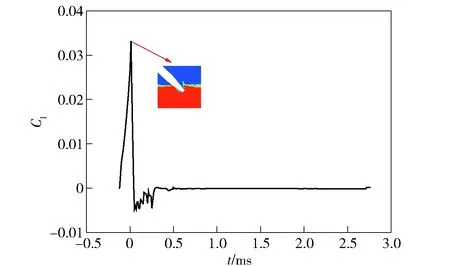
图15 升力系数随时间变化Fig.15 Lift coefficient versus time
图16给出了力矩系数随时间变化曲线。由图16可知:力矩系数在重力和流体动力的共同作用下,在入水初期有两个峰值;入水初期运动体发生俯仰运动的趋势较大,之后随着空泡将运动体包裹完全,力矩系数也趋于平稳。
通过对运动体头部上、中、下3点的压力进行监测发现,头部压力最大值pmax出现在头部中点位置,图17所示为头部中点压力随时间的变化曲线。从图17中可以看到,类似于阻力系数曲线随时间的变化趋势,运动体在空气中运动时头部压力较小,在入水撞击阶段受到巨大的入水砰击压力,流动形成后头部压力随着运动体入水的深入逐渐减小。运动体头部在撞击阶段受到约16 MPa的极强压力载荷,即使在流动形成之后压力载荷也在10 MPa左右,因此高速入水运动对运动体头部的强度要求较高。
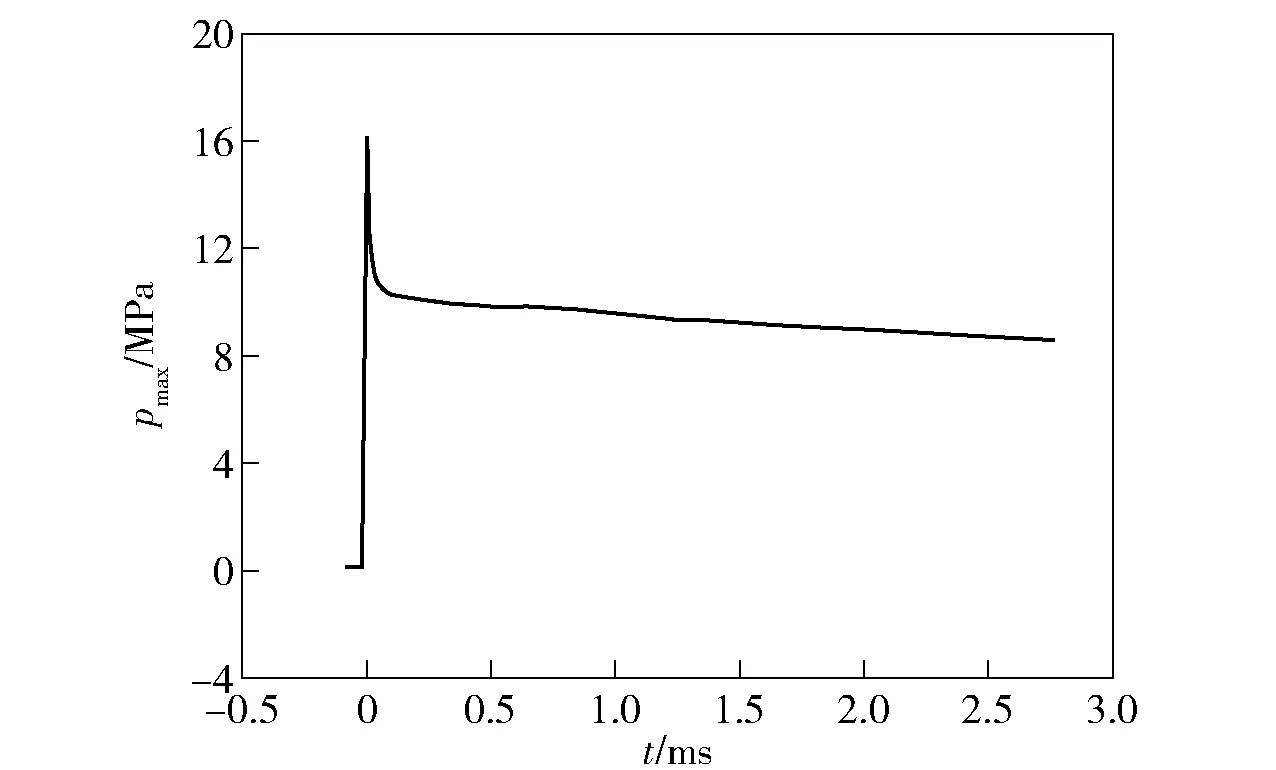
图17 头部中点压力随时间变化Fig.17 Pressure on nose versus time
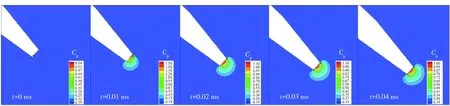
图18 头部压力系数云图随时间变化Fig.18 Pressure cofficient of nose versus time
2.2 入水过程流场结构特性与空泡发展分析
图18为运动体头部压力系数分布云图,其中压力系数Cp=2(p-p∞)/(ρv2),p∞为远场压力。由图18可知,当头部下端与水面接触时边缘压力尚未达到最大值,随着运动体继续进入水中,头部所受压力迅速增至最大值。高压区域的云图为半球形,且逐渐由运动体头部下侧向头部中点移动,最终呈对称分布,此时头部所受最大压力也趋于一个相对稳定的值。当运动体头部完全沾湿后,不同时刻的压力峰值均出现在头部中点位置。
图19为水下1.5L位置处空泡剖面的速度矢量图,图中箭头的长度越长,表示该位置的速度越大,具体数值参考图中左侧的图例。从图19中可以看出,1.5L位置处的空泡直径有一个由小变大再变小的过程。这是因为当运动体头部运动至1.5L附近时(t=1.6 ms),运动体传递给附近流体的动能较大,此时空泡壁面上的速度值较大,且速度方向指向水中,表明该位置的空泡具有较大的扩张速度,同时还具有随弹体运动的向前速度。随着运动体运动的深入,该位置处空泡附近的流体获得的动能减少,空泡壁面上的速度值逐渐减小,且沿运动体运动方向的速度分量逐渐减少,空泡壁上的速度方向与空泡剖面趋于平行。随着空泡壁面速度值的减小,空泡剖面平面内的速度方向从最初的指向水中逐渐指向空泡内(t为2.7~2.9 ms),表明空泡由扩张状态向紧缩状态过渡。这主要是由空泡附近的流体动能减少以及空泡内外压力差的共同作用下导致的。
自由液面位置空泡口形态的变化如图20所示。不同于小型回转体垂直入水产生的圆形空泡口,倾斜入水产生的空泡口为近似椭圆形;而且随着运动体入水的深入,空泡口形态的发展过程与图19中显示的水下1.5L处空泡发展过程类似,空泡口不断扩张至最大尺寸,之后在表面张力及流体动力的共同作用下逐渐收缩,直至水下空泡从自由液面拉脱。
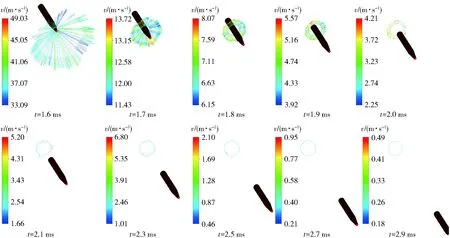
图19 水下1.5L处空泡剖面速度矢量图Fig.19 Contour of velocity vector on cavity wall for x=1.5L
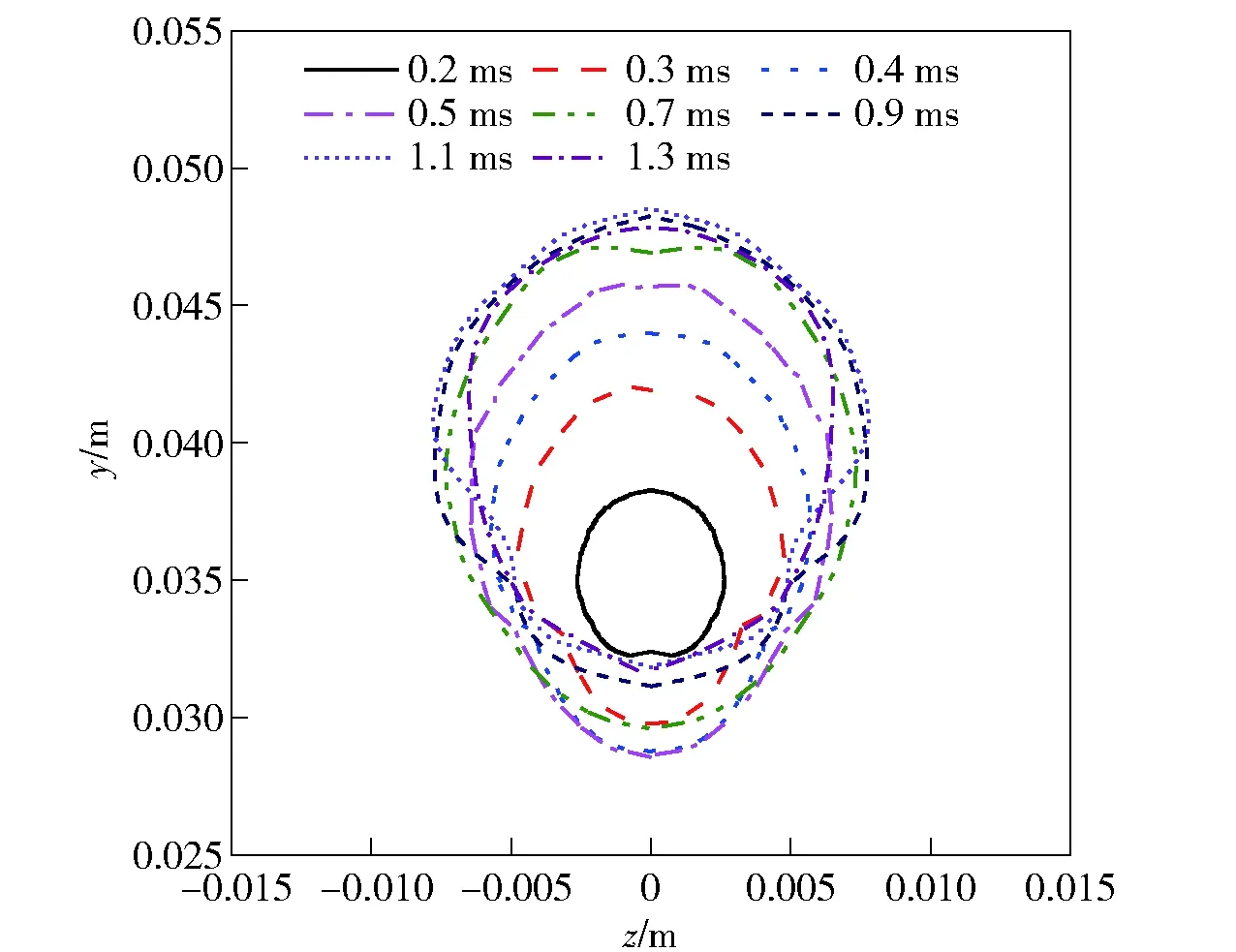
图20 空泡口形态随时间变化Fig.20 Cavity mouth shape versus time
2.3 入水角度对入水流场的影响分析
本节采用图1中的模型分别开展入水角度为15.0°、30.0°、43.6°以及60.0°的倾斜入水数值模拟,初始入水速度均为141.15 m/s.
2.3.1 入水角度对流体动力特性的影响
根据现有文献[25-26]可知,运动体阻力系数主要是受运动体结构外形的影响,而与运动体速度无关,但入水角度对阻力系数的影响尚未可知,因此本文针对该问题进行了数值计算与结果分析。
由图13已知,运动体入水过程中阻力系数会在运动体触水瞬间达到一个最大值,而当运动体被空泡完全包裹后阻力系数会维持一个稳定值。图21为入水撞击阶段阻力系数最大值以及运动体带空泡运动稳定阶段阻力系数与入水角度变化曲线。从图21中可以看出,阻力系数最大值随入水角度的增加而增加,这是因为入水角度越大时运动体头部截面与自由液面接触的面积越大,受到沿速度方向反向的入水冲击力越大,从而导致运动体触水时阻力系数的最大值越大。不同于阻力系数最大值的变化趋势,由于空泡已经形成且完全包裹运动体,此时阻力系数小于触水时的阻力系数峰值,且阻力系数趋于一个定值,基本不随入水角度的改变而变化。
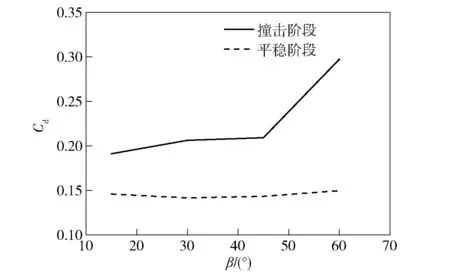
图21 阻力系数随入水角度变化Fig.21 Drag coefficient versus entry angle
图22为运动体入水撞击阶段力矩系数最大值以及平稳阶段力矩系数随入水角度变化曲线。由图22可知,不论是力矩系数峰值还是运动平稳阶段的力矩系数,均随着入水角度的增大而减小,表明入水角度越小,运动体越容易发生俯仰运动,越容易发生弹道偏移。由于力矩系数为正值,带空泡运动阶段的运动体有抬头运动的趋势,姿态角随着运动的继续而减小。
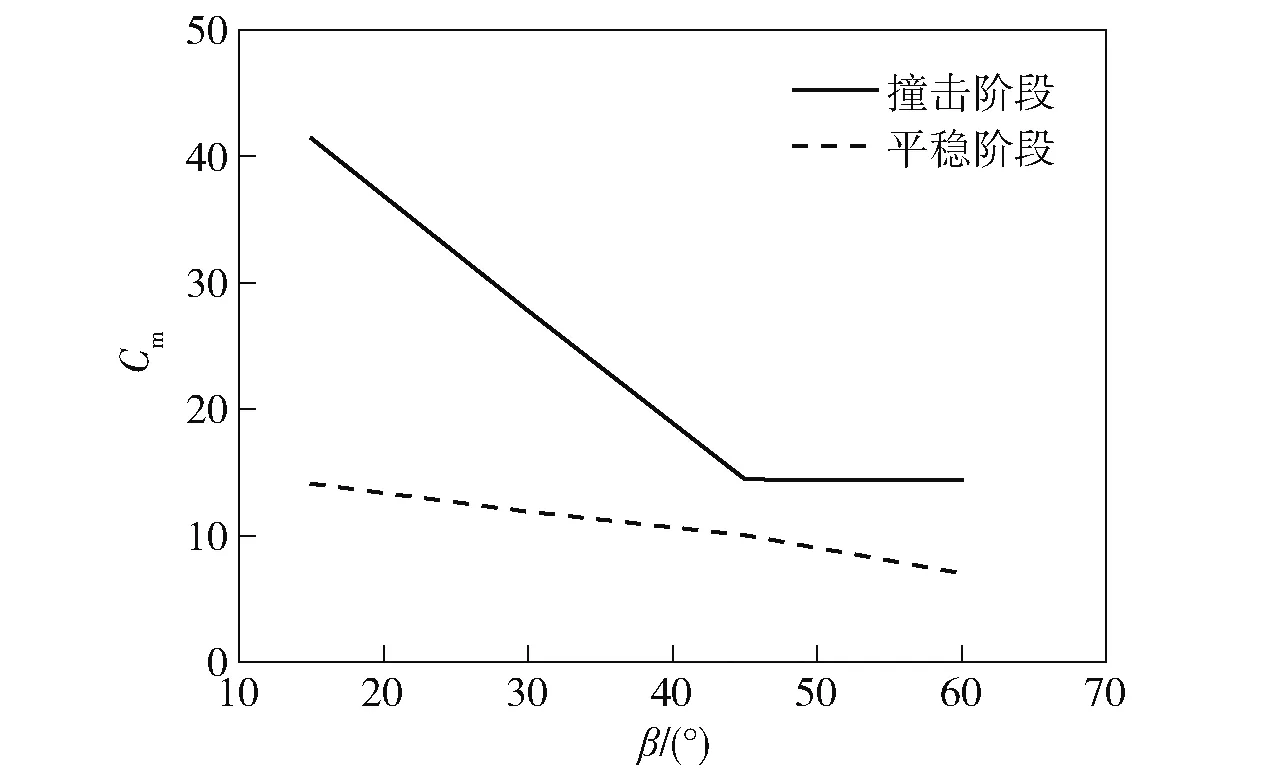
图22 力矩系数随入水角度变化Fig.22 Moment coefficient versus entry angle
图23给出了入水撞击阶段运动体头部中点压力最大值随入水角度变化曲线。由图23可知,压力峰值随着入水角度的增大而增大。这是因为入水角越大,头部受到由于运动体撞击自由液面产生的射流冲击越大,头部沾湿区域也随着增加,从而使头部压力峰值较大。因此,越是较大入水角度的倾斜入水运动,越要加强运动体头部的结构强度。
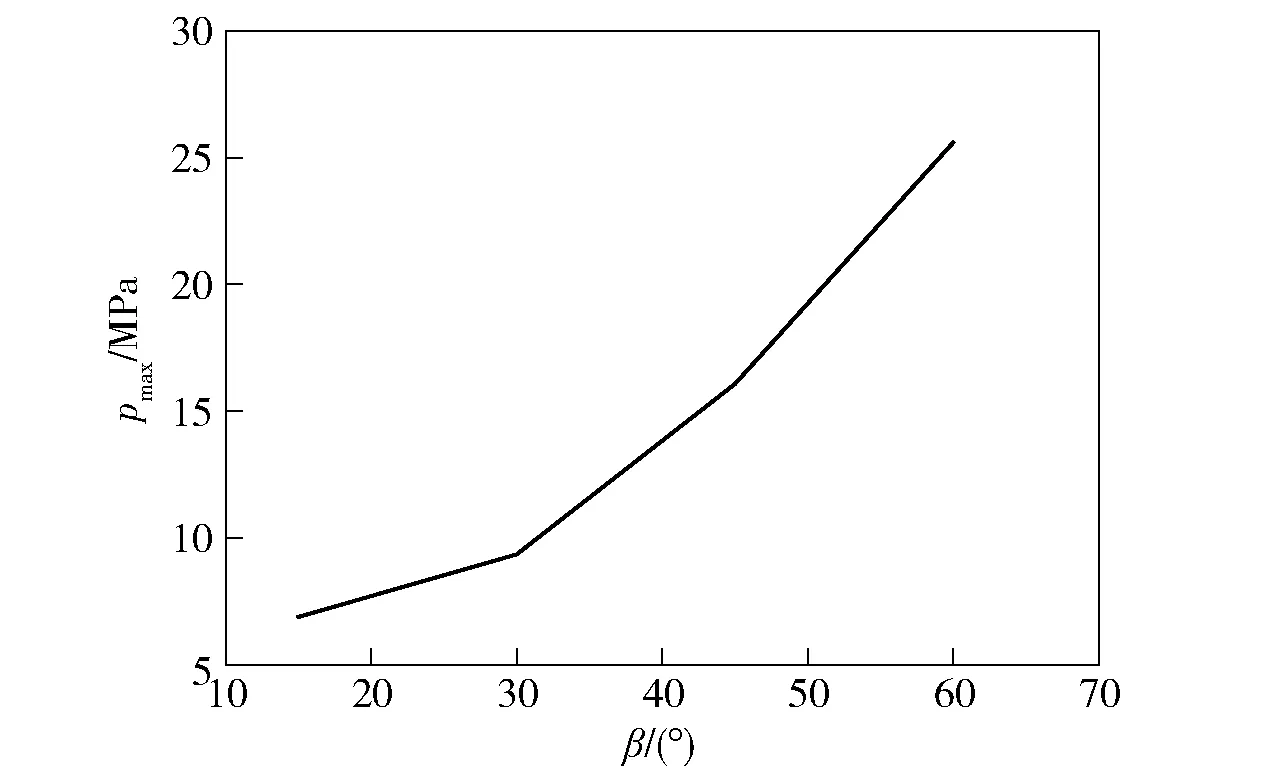
图23 头部压力随入水角度变化Fig.23 Maximum pressure versus entry angle
2.3.2 入水角度对空泡发展的影响
空泡形态对跨介质运动体的外形设计有着至关重要的影响,运动稳定性取决于空泡长度能否包裹住整个运动体,而空泡直径则对运动体能否沿直线运动有着巨大影响[27]。
图24为运动体运动速度随时间变化曲线。由图24可知,运动体以不同入水角度入水的速度变化趋势一致,在入水前由于空气中阻力比水中的阻力小得多,因此速度衰减不明显,而入水后速度迅速衰减。图24中的局部放大图为运动体撞击阶段的速度变化曲线,由局部放大图可知,入水角越大,速度衰减越快。这一规律与图21中所示撞击阶段阻力系数随入水角度变化的规律一致。
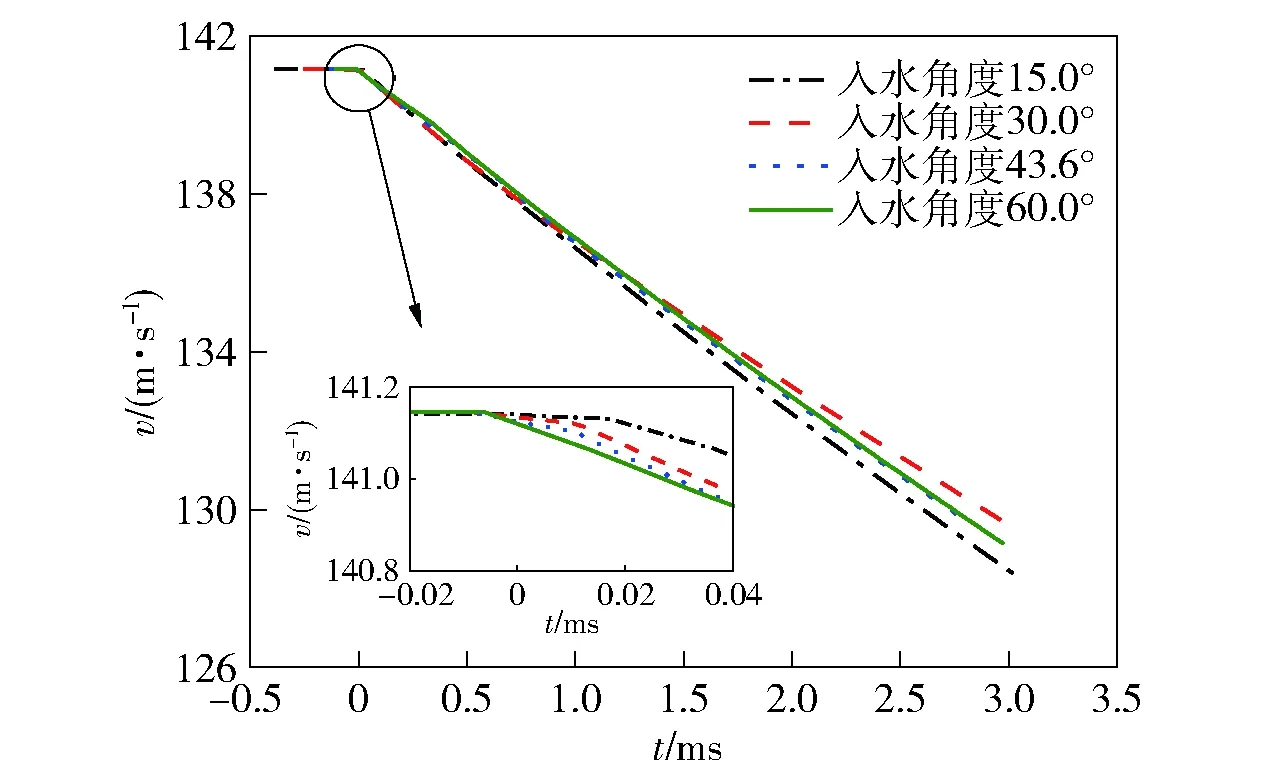
图24 运动速度随时间变化Fig.24 Velocity versus time
图25为运动体入水位移分别为1L、2L及3L时的空泡形态对比图。由图25可见,原本静止的流体在运动体挤压下获得动能并开始向四周运动,从而在水中形成与大气相连的入水空泡,此时高速运动的运动体夹带大量的空气进入空泡内,同时由于空化效应产生的水蒸汽也不断填充至空泡内,使空泡逐渐扩张。从图25中可以看出,当空泡长度相同时,空泡下方(即远离自由液面的一端)的直径基本相同。然而,空泡口的长度(即椭圆形空泡口的长轴长度,见图26)则随着入水角度的减小而增大。这是因为运动体运动至相同位移时的速度基本一致,从能量守恒角度考虑头部附近空泡的扩张速度[25]几乎相同。但当运动体以不同角度入水时,较小的入水角度导致运动体在自由液面平面内的投影面积较大,从而造成较大的空泡口长度。另外,较大的空泡口需要较长时间来覆盖,因此入水角度越小,空泡口进入收缩阶段越慢,空泡拉脱现象发生得越晚。
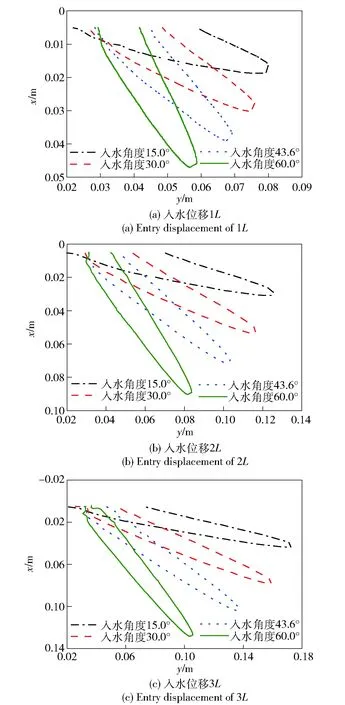
图25 空泡形态对比Fig.25 Comparison of cavity shapes
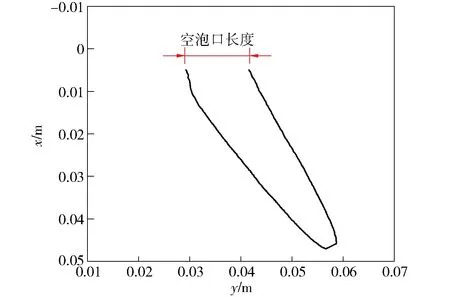
图26 空泡口长度示意图Fig.26 Schematic diagram of cavity mouth
图27为入水过程中空泡的最大直径与最大长度随入水角度变化曲线,其中Lc,max为最大空泡长度,Dc,max为最大空泡直径。由图27可知,空泡的最大直径与最大长度均随着入水角度的增加而减小。当空泡发生拉脱现象后,进入空泡内的空气就被完全阻断。由图25可知,入水角度越小,空泡发生拉脱现象越晚,因此在入水速度相同条件下,入水角度越大,夹带进入空泡内的空气量越小,空泡膨胀的程度越小,入水形成的最大空泡尺寸越小。
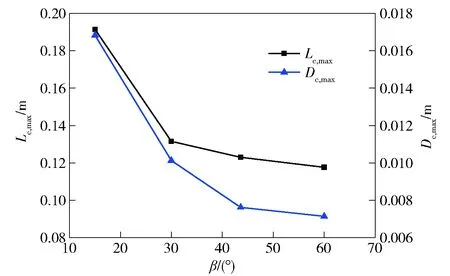
图27 最大空泡尺寸随入水角度变化Fig.27 Maximum cavity size versus entry angle
3 结论
本文针对小型运动体高速倾斜入水问题开展了数值模拟,并将计算结果与实验结果进行了对比,验证了本文数值方法的正确性。在此基础上对入水过程中的流体动力特性、流场结构特性以及空泡发展进行了分析;同时开展了入水角度对入水多相流场特性的影响分析。所得主要结论如下:
1)运动体在入水初期受到的阻力、升力及力矩较大且存在波动,但之后随着空泡的形成各系数逐渐趋于定值;运动体头部在入水撞击阶段受到约16 MPa的极强载荷,因此要求高速入水的运动体具有足够的强度。
2)运动体头部的高压区呈半球形,且由头部下端向中点移动,入水过程中的压力峰值位于头部中点;空泡壁面的速度方向随着运动体运动的深入,先指向水中随后指向空泡内。
3)入水角度越小,撞击阶段的阻力系数越小,入水砰击压力越小,运动体入水后越容易发生弹道偏移;但在空泡形成且完全包裹运动体后,入水角度对阻力系数的影响很小。
4)当入水空泡长度相同时,入水角度越小,空泡口长度越大,拉脱现象发生得越晚;入水空泡的最大长度及最大直径随入水角度的增加而减小。
