固定翼垂直起降无人机过渡机动优化控制分配研究

2019-03-13刘真畅唐胜景李梦婷王肖郭杰

兵工学报 2019年2期

刘真畅，唐胜景，李梦婷，王肖，郭杰

(北京理工大学宇航学院，北京 100081)

0 引言

随着社会的发展，无人机在军事和民用领域得到广泛应用。在无人机众多的应用场景中，低空复杂环境将成为无人机的一个应用热点。本文所研究的固定翼垂直起降无人机[1]可以凭借垂直起降功能摆脱起降场地约束，可以通过固定翼飞行功能进行高效巡航，也可以利用过渡机动功能在城市低空等复杂飞行环境中进行低速规避飞行[2]。在过渡飞行过程中，无人机气动舵面操纵效率较低、升力较小，需要通过发动机矢量喷管与气动舵面对飞机姿态进行组合控制，并利用发动机推力补足升力。因此推力矢量和直接力控制技术在过渡飞行过程中起到重要作用。由于无人机采用了气动力、推力矢量复合控制方法，控制系统中的控制通道映射关系在不同飞行状态下会发生明显变化，控制量相互耦合且存在冗余，使无人机动力学特性具有明显的非线性特征。

目前无人机过渡过程控制技术已经在采用升力风扇+推力矢量发动机的固定翼无人机[2-5]、倾转旋翼无人机[6-7]、尾座式无人机[8]、涵道飞行器[9]、旋翼复合翼垂直起降飞行器[10]等不同平台上开展了研究。文献[2]运用非线性动态逆(NDI)方法对无人机进行过渡机动控制，采用序列二次规划(SQP)非线性优化求解方法对耦合且冗余的控制量进行分配。但是非线性优化分配需要迭代求解，对控制器在线计算能力有较高的要求。文献[3]运用增量动态逆(INDI)方法研究过渡飞行时人在回路的控制方法，将过渡过程操控进行分段化处理，在控制器中针对不同飞行阶段提前设计好各通道控制映射，并通过飞行速度间接求出发动机推力分量。该方法具有控制器设计简单、计算量小的特点，但是没有考虑过渡机动过程中直接力和气动力的优化分配问题。文献[4]基于NDI方法研究了过渡过程的纵向平面3自由度航迹控制问题，通过纵向和横向解耦将控制问题简化，不适用于无人机在过渡机动状态进行6自由度高机动飞行。文献[7]研究倾转4旋翼过渡飞行状态的航迹、姿态控制问题，采用线性化方法将控制问题解耦，并利用伪逆法求解控制分配问题。目前大部分文献通过控制模型分段化、纵向和横向解耦、将部分冗余控制量当作已知量的方法将控制模型简化，期望过渡飞行过程尽可能短暂平稳，没有充分发挥无人机引入直接力控制后具有的非常规机动潜力。

INDI控制技术是一种基于NDI思想对控制方程中的增量进行求解的方法。该方法可以将控制模型在增量形式下线性化，并保持模型原有的非线性特性。同时INDI方法可以降低控制系统对气动模型精确度的依赖，减少控制系统设计中的不确定性。目前INDI方法已经应用于多旋翼无人机[11-12]、无人直升机[13]、固定翼无人机[14]、导弹[15]等平台上。

本文利用INDI方法构建无人机6自由度控制模型，根据推力矢量无人机特点引入直接力控制技术，重点研究航迹跟踪过程中的非线性控制和控制分配问题，实现无人机不同飞行阶段的全局控制。相比于文献[14]中将侧滑角近似为0°的航迹INDI控制方法，本文考虑了引入3轴向直接力控制后侧滑角较大的过渡机动控制问题。针对无人机控制冗余问题，本文提出2级递进式优化控制分配策略，以非线性优化分配和改进链式递增相结合的控制分配方法，在航迹层针对气动力和推力矢量进行第1次控制分配，在姿态层面对气动力矩和推力矢量力矩进行第2次分配，从而综合求解出各执行机构输出。在优化控制分配求解中采用松弛约束策略，在减少计算量的同时确保了控制分配结果的合理性。本文针对优化分配中的权值选取问题提出自修正层次分析法，使控制器能够根据任务需求和飞行状态自动调整权值选取策略，使优化分配结果更具有目的性。最后进行过渡机动航迹跟踪仿真，评估控制系统及控制分配算法的有效性，并验证了无人机在低空复杂飞行环境下的低速高机动能力。

1 固定翼垂直起降无人机

固定翼垂直起降无人机采用串置翼升力体气动布局。该布局可以在有限翼展下为无人机提供更大的升力，使其适用于低空复杂飞行环境。无人机动力系统由1台升力风扇和2台推力矢量发动机组成，如图1所示。升力风扇下方有通过转动轴连接的控制舵面，控制舵面可以左右偏转45°，为无人机提供侧向控制力和偏航力矩。发动机矢量喷口可以向上偏转15°、向下偏转90°，为无人机提供x轴方向和y轴方向推力以及3轴向控制力矩。升力风扇+推力矢量发动机的动力系统设计可以使无人机具有垂直起降、过渡飞行、巡航功能。

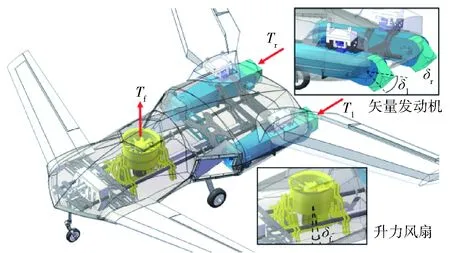
图1 无人机总体布局示意图Fig.1 UAV configuration

图1中：Tl、Tr和Tf分别为左发动机推力、右发动机推力和升力风扇推力；δl、δr和δf分别为左矢量喷口偏角、右矢量喷口偏角和升力风扇矢量舵偏角。垂直起降无人机在过渡飞行过程中受到的气动干扰及不确定性包含垂直起降过程中地面喷流效应、大攻角飞行时的湍流效应、发动机吸气效应、矢量喷口偏转推力折损效应等。在未进行风洞实验的情况下，通过气动估算、计算流体力学(CFD)计算、飞行参数辨识的综合方法获取无人机气动数据[1-2]。实际气动力与估算气动力间的不确定性误差将在INDI控制器中进行分析。采用气动参数最小二乘多项式拟合方法，获得无人机气动力、气动力矩与控制量间的多项式描述形式，以满足控制分配算法的计算。无人机基本参数如表1所示。

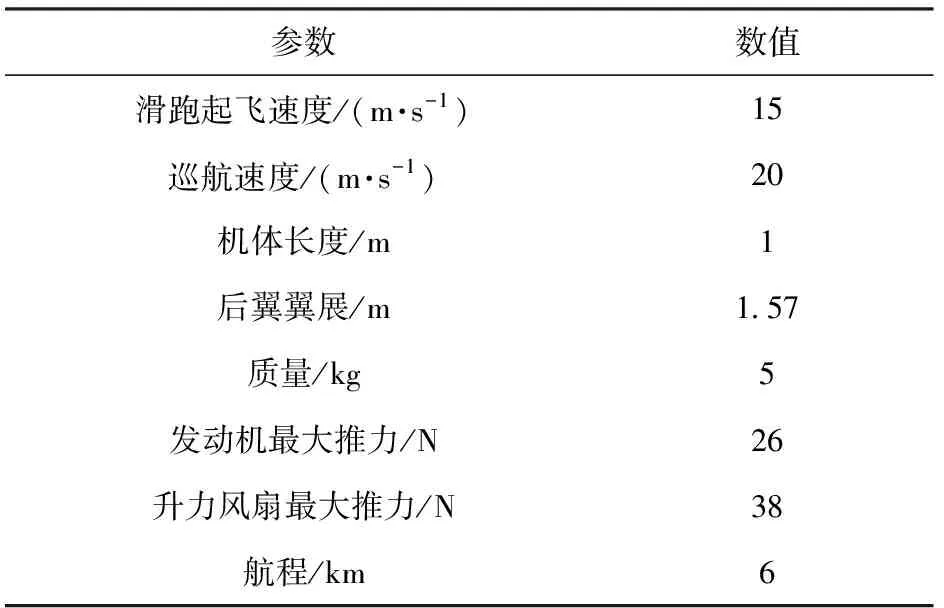
表1 无人机基本参数

2 INDI控制

本文根据时标分离法将无人机航迹控制回路分为4个子回路，由慢到快依次为飞行器质心移动运动学(航迹运动学)回路、飞行器质心移动动力学(航迹动力学)回路、飞行器绕质心转动运动学(姿态运动学)回路、飞行器绕质心转动动力学(姿态动力学)回路。控制器以上一回路的输出作为下一回路的输入，进行递进式求解。INDI控制方法能够消减系统的不确定性，使控制量解耦。考虑到控制系统中由气动力、气动力矩估算误差造成的不确定性只存在于航迹动力学回路和姿态动力学回路中，因此只针对这两个回路采用INDI控制，其余回路采用NDI控制。控制结构图如图2所示。

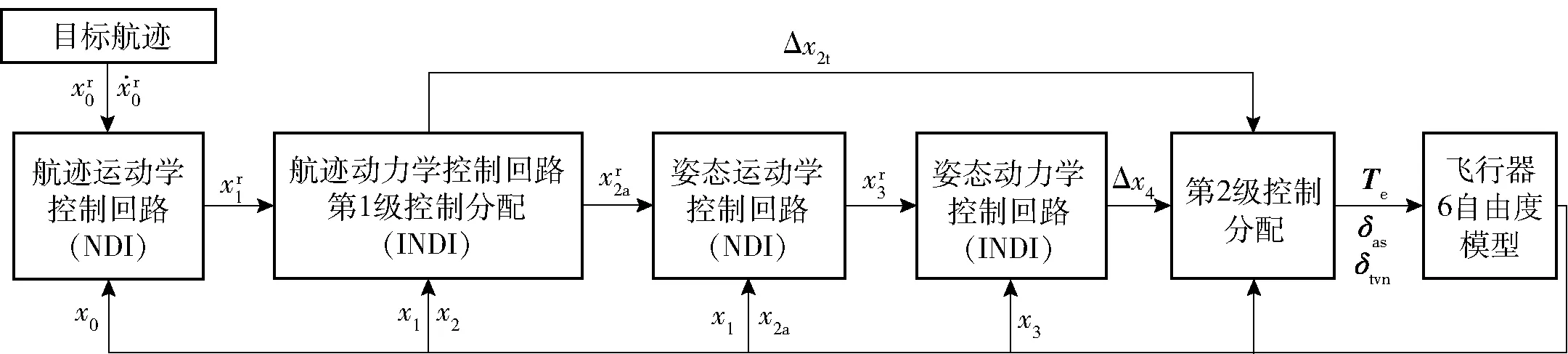
图2 控制结构图Fig.2 Block diagram of control system

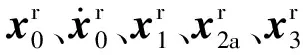
(1)

式中：x0为位置矢量；x、y和z为无人机在地面坐标系中北、东、地方向的坐标。

(2)

式中：x1为速度矢量；v为无人机速度标量；χ为航迹偏角；γ为航迹倾角。

(3)

式中：x2为航迹动力学回路控制量；x2a为姿态矢量；x2t为推力矢量；α为攻角；β为侧滑角；μ为航迹滚转角；Tx、Ty和Tz分别为发动机推力在机体坐标系轴向投影。

(4)

式中：x3为角速度矢量；p、q和r分别为角速度在机体坐标系轴向投影。

(5)

式中：x4为控制力矩矢量，由气动控制力矩x4s和推力矢量控制力矩x4t组成；lc、mc和nc分别为控制力矩沿机体坐标系轴向的投影。

(6)

式中：Te为动力系统推力控制量；δtvn为动力系统矢量喷口控制量；δas为气动舵控制量；δa、δe和δr分别为滚转角、俯仰角、偏航气动舵偏角。

2.1 基本原理

(7)

(8)

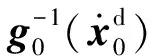
在航迹动力学回路中x1为被控量、x2为控制量。控制方程如(9)式～(11)式所示：

(9)

f1(x1)=PLkgG，

(10)

g1(x1,x2)=P(Lkbx2t+LkaFa)，

(11)

(12)

对x1n在点(x1,x2)处进行泰勒展开，并忽略高阶小量，可表示为

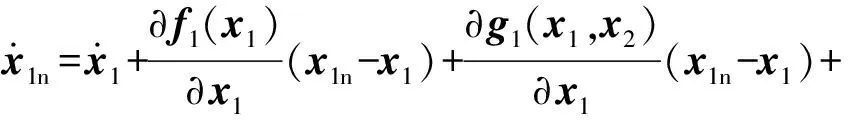
(13)

(13)式中第2项和第3项是关于x1的偏导数，第4项是关于x2的偏导数。根据时标分离法原则，在质心移动动力学回路中x1的偏导数相比于x2的偏导数是小量，可忽略不计。将第4项展开后可得

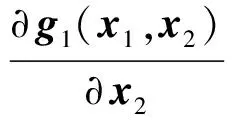
(14)

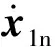
(15)

式中：K1为控制增益矩阵。

将(14)式、(15)式代入(13)式中并进行简化，可得

(16)

将(16)式进一步展开，并认为x2中元素的增量相乘为高阶小量，如(17)式所示：

Δx2iΔx2j=0，

(17)

式中：i、j取值为1到6的自然数，代表向量x2中的元素序号。

整理后控制方程可写为增量标准形式，如(18)式所示:

(18)

式中:g1a和g1t为3×3阶矩阵，分别为气动力和发动机推力矢量的控制矩阵。求加权伪逆后计算出控制量的增量如(19)式所示：

(19)

(20)

在姿态运动学回路中，控制方程可写为

(21)

通过NDI方法可求得参考角速度矢量为

(22)

在姿态动力学回路中控制方程可写为

(23)

f3(x3)=J-1(Ma-x3×Jx3)，

(24)

式中：J为转动惯量矩阵；Ma为除舵面偏转产生的控制力矩外的所有气动力矩总和。由于f3(x3)中Ma的计算误差会给控制回路引入不确定性，对该控制回路采用INDI方法求得

(25)

在控制系统中，航迹动力学回路的输出Δx2t和姿态动力学回路的输出Δx4均为虚拟控制量，它们在第2级优化控制分配中将被用于联立求解Te、δtvn、δas.

2.2 不确定性分析

在航迹动力学回路中控制系统的不确定性主要是由对气动力Fa的计算误差引起的。Fa精度取决于气动参数获取的准确度。在本文研究中对气动参数进行如下处理：

(26)

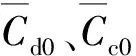
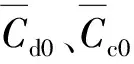
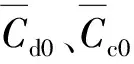
在具有控制冗余的航迹动力学回路中使用INDI方法相比NDI方法具有如下两大优势：1)INDI方法将气动力造成的不确定性仅局限在气动力控制矩阵g1a中，隔绝其对直接力增量控制影响；2)INDI控制方法可以将g1(x1,x2)中的控制量解耦，便于之后关于x2中直接力控制量Tx、Ty、Tz和气动力控制量α、β、μ进行控制分配求解，避免了非线性耦合控制分配问题的复杂数值求解，降低了控制系统的计算负担。

同理，在姿态动力学回路中，气动力矩系数处理方法与气动力系数类似，如(27)式所示：

(27)

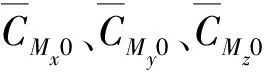
(28)

(29)

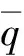
(25)式中通过INDI方法成功消除了含有Ma的f3(x3)项，大大简化了姿态动力学回路的不确定性。

2.3 状态导数延时性分析

(30)

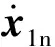
(31)

(32)

航迹动力学回路控制流程如图3所示，其中x2af为x2a滤波后的结果。

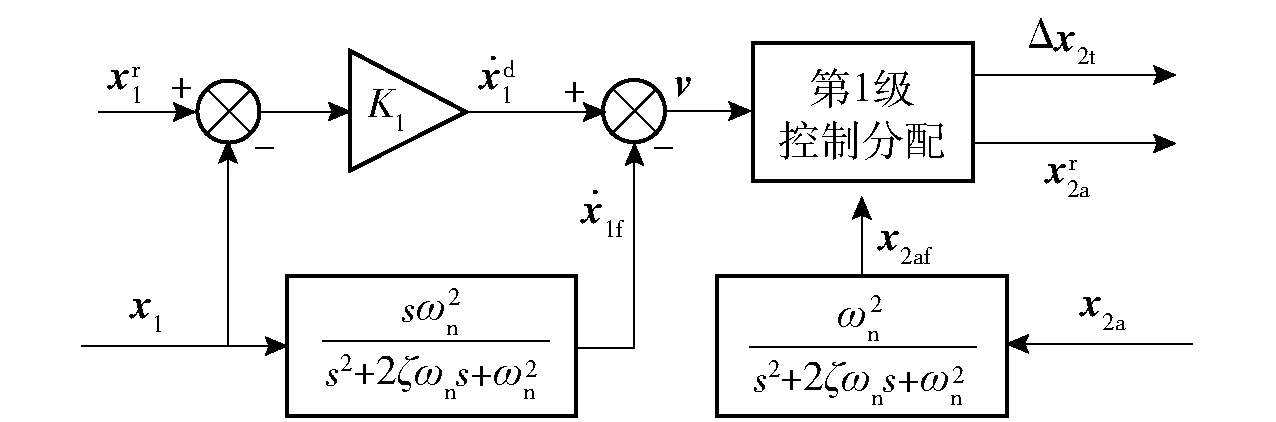
图3 航迹动力学回路控制流程图Fig.3 Flow chart of flight path dynamic control loop

(33)

姿态动力学控制流程图如图4所示。

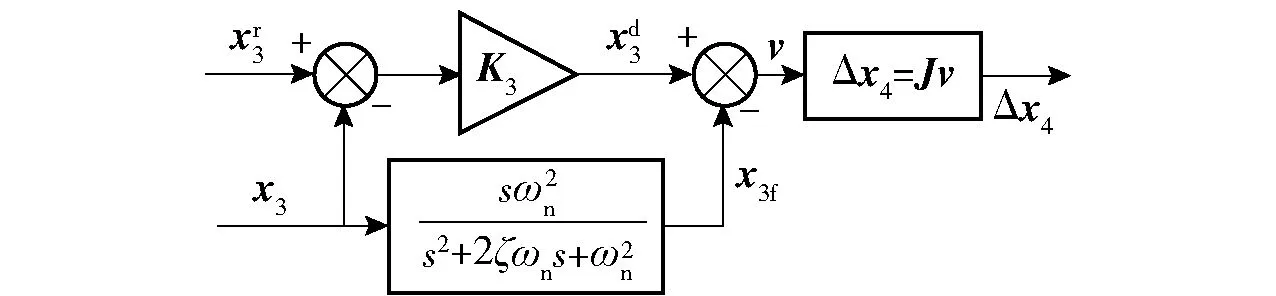
图4 姿态动力学回路控制流程图Fig.4 Flow chart of attitude dynamic control loop

3 2级递进式优化控制分配方法

在控制系统设计中需要对航迹动力学回路和姿态动力学回路中的冗余控制量x2和x4进行分配。由于x2的分配结果会对Δx4产生影响，并且需要根据Δx2t和Δx4t综合求出动力系统Tl、Tr、Tf、δr、δl、δf的分配情况，因此本文基于INDI控制方法，提出2级递进式优化控制分配方法，以解决无人机航迹、姿态复合控制分配问题。

3.1 第1级优化控制分配

3.1.1 增量加权伪逆法

基于航迹动力学回路中采用的INDI控制方法，本文提出增量动态加权伪逆方法对Δx2进行控制分配。设：

(34)

结合(34)式和(18)式，在不考虑执行机构饱和情况下，优化问题可以写为

(35)

式中：Δx2为优化变量；x2f和ν为已知量；W1和W2为权值的对角矩阵，它们在每次优化分配时动态生成。目标函数的第1项用于限制实际控制量x2的大小，第2项用于限制控制量的变化速率。将(35)式展开推导后，得出优化问题等价于：

(36)

式中：

(37)

(38)

通过优化问题的最小范数解可求得

Δx2=Gν+(GB-I)x20，

(39)

G=W-1(BW-1)†，

(40)

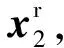
(41)

在第1级控制分配中不对Δx2t进行限幅，将其作为虚拟控制量传递到第2级控制分配中，与Δx4t联合求解出动力系统Tl、Tr、Tf、δr、δl和δf的期望值后，再结合实际情况进行限幅。

3.1.2 自修正权值选取策略

在控制分配过程中通过权值描述控制变量重要度的差异性，但控制变量的重要度也随着飞行状态和任务需求的变化而变化，因此本文设计了一种动态权值选取策略，使控制器能够针对不同飞行状态和任务需求合理地优化控制分配结果。

设计控制变量的权值需要基于现实需求衡量目标控制变量相对于其他控制变量的重要性。权值的选取没有绝对的衡量准则，只能根据不同的应用需求通过人为经验进行模糊判断。一般难以从全局衡量每个控制变量的重要度，但是容易判断出每两个控制变量间的重要关系。通过层次分析法(AHP)可以通过比较每两个控制变量间的重要度综合求出控制变量的权值。

针对本文研究问题，(35)式中的权值选取矩阵可表示为

W1=diag(Wα,Wβ,Wμ,WTx,WTy,WTz) ，

(42)

W2=diag(WΔα,WΔβ,WΔμ,WΔTx,WΔTy,WΔTz)，

(43)

式中：Wi代表其下标所对应变量的权值。根据控制变量的特点将它们分类到不同集合S中，根据集合从属关系将它们划分3个层次，称为权值结构，如图5所示。图5中wi代表1层集合权值，wij代表第2层集合权值，wijk代表第3层元素权值。

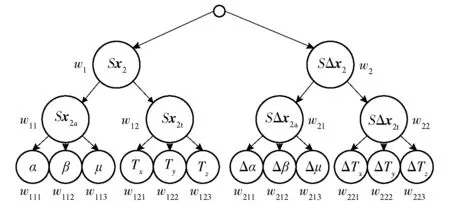
图5 权值结构示意图Fig.5 Illustration of weight structure

本文将权值的求解问题分为3个层次进行分别评估，每一层中集合和元素的权值满足以下要求：

1)处于同一集合内的权值要进行归一化处理：

(44)

式中：i为图5中第1层集合序号；j为第2层子集序号；k为第3层元素序号。

2)第1层、第2层的权值wi和wij满足

w1,w2,w11,w12,w21,w22∈{0∶0.01∶1}.

(45)

3)第3层权值wijk通过判断矩阵求出。关于AHP判断矩阵的计算方法在文献[16-17]中有详细介绍。最终根据各层权值，目标函数的权值计算可表示为

(46)

式中：Wi(k,k)为权值矩阵Wi中的第k行第k列元素，k=1，2，3. (42)式～(46)式描述了权值结构及其计算方法，在实际控制分配过程中需要控制器根据当前飞行状态和任务需求对权值结构生成初值，并根据控制饱和情况对权值进行动态调整。本文在权值结构基础上分别设计权值生成器和权值调整器，以实现权值自修正功能。

权值生成器的功能是在每次优化计算开始前，根据当前飞行状态和任务需求生成权值。在飞行状态方面考虑速度对权值的影响，选取速度分别为5 m/s、10 m/s、15 m/s、20 m/s和25 m/s作为算例。任务需求方面考虑直接力控制程度对权值选取的影响，直接力控制程度h∈[0,1]，取0、0.5、1共3个状态作为算例。针对以上算例的15种组合方法，根据人为经验和仿真测试分别离线生成对应的权值数据结构，并将它们存入知识库中。在实际控制分配中根据速度信息和直接力控制程度，在知识库中通过插值法在线生成当前状态权值。

权值调整器的功能是当优化变量的求解结果超出实际约束范围时对权值进行在线调整。权值变动会对优化控制分配结果产生明显影响，权值突变会引起飞行状态震荡或发散。因此权值调整器的另一个功能是确保权值变化的连续性。通过权值调整器对每个控制变量的连续饱和次数进行计数，定义每个控制变量的连续饱和次数为nijk(i,j=1,2，k=1,2,3)∈N，N为自然数，如果控制变量上一时刻达到饱和而当前时刻未饱和，则计数器清零。当控制变量出现连续饱和时，权值调整器会根据饱和次数对相关权值在每个控制周期内进行微小等幅调整。第1级优化控制分配和动态权值调整策略的工作原理如图6所示。

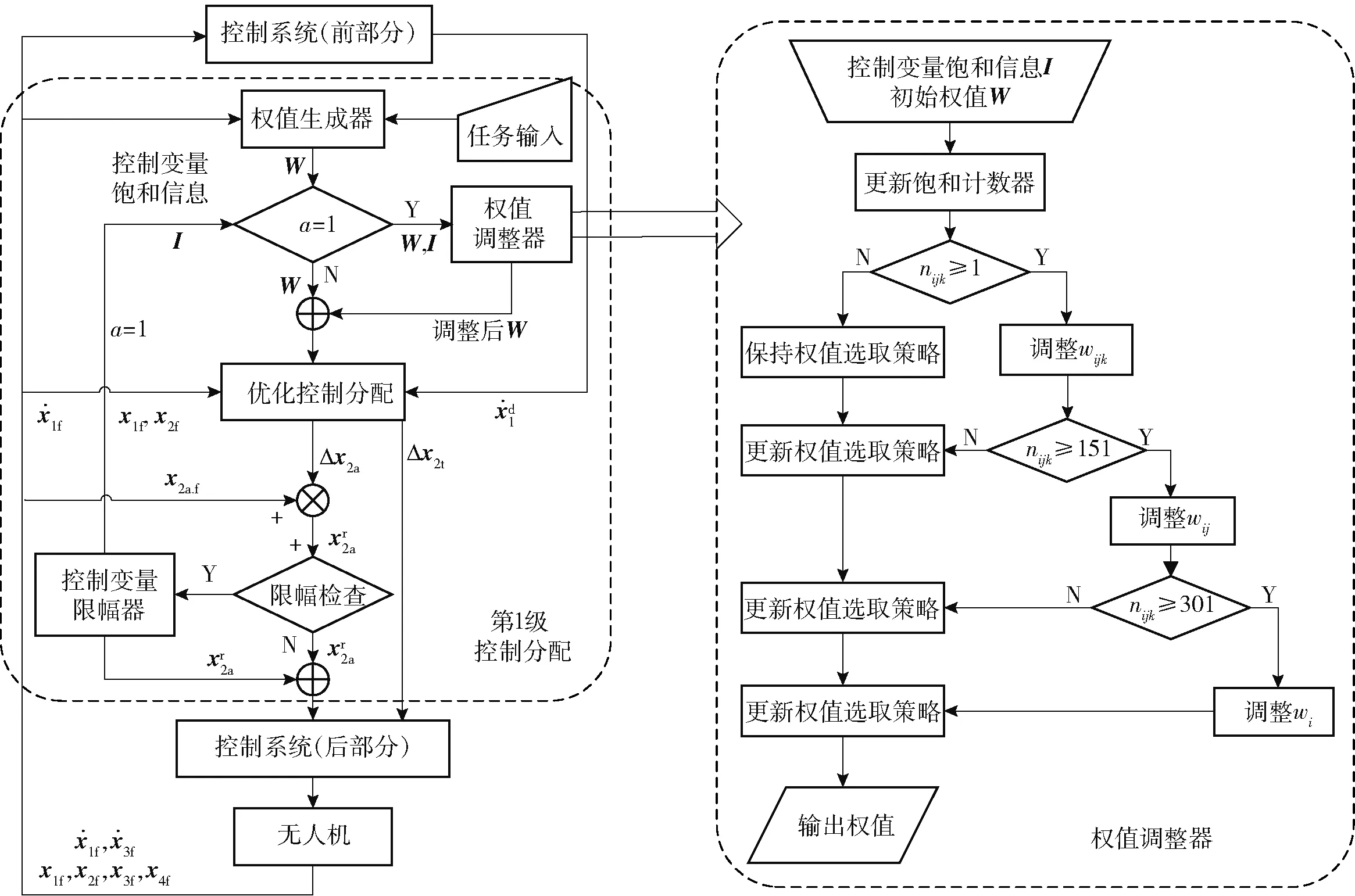
图6 第1级优化控制分配及动态权值调整策略流程图Fig.6 Flow chart of first stage optimal control allocation and dynamic weight adjusting strategy

图6中nijk的选取范围一般根据飞控系统的控制频率选取。如果飞控系统的控制频率为100 Hz，则控制分配每0.01 s执行一次，某控制变量持续饱和超过3 s(nijk>300)时控制系统即对权值进行全局动态调整，使控制分配适应当前飞行状态的需求。nijk设置范围如果过大会造成权值调整缓慢，控制机构持续饱和可能会造成飞行器严重偏离目标航迹。nijk设置范围如果过小则会造成权值调整速度过快，目标函数的快速变化会造成飞行器抖振及控制发散等恶劣情况。

3.2 第2级增量控制分配

第2级增量控制分配是根据航迹动力学回路中第1级控制分配求出的Δx2t和姿态动力学回路求出的Δx4，对气动舵控制量δas、矢量喷口偏角δtvn、发动机推力Te进行控制分配。

无人机动力系统模型可以表示为

(47)

(48)

式中：dxt、dxf分别为沿机体x轴方向矢量喷口与升力风扇到质心距离；dyt为沿机体y轴方向矢量喷口到质心距离。为了保持INDI控制的时间一致性，执行机构模型的输出需要经过一个2阶滤波获得Te，f、δtvn，f和δas，f. 根据(49)式用链式递增法对Δx4进行控制分配，设定气动力矩控制优先级高于推力矢量控制力矩，当气动舵达到控制饱和后再引入发动机力矩控制，分别求出Δx4s和Δx4t.

Δx4=Δx4s+Δx4t，

(49)

通过(50)式求得气动舵控制量增量Δδas：

(50)

气动舵的参考输出可表示为

(51)

将(47)式和(48)式联立写成增量形式，将2个及2个以上的增量相乘视为高阶小量并进行忽略，整理后如(52)式所示：

(52)

式中：Ge为6×6阶矩阵，矩阵中的元素由Te，f、δtvn，f中的元素计算获得。

通过矩阵求逆可直接求出ΔTe和Δδtvn，如(53)式所示：

(53)

矢量发动机系统参考输出可以根据(54)式和(55)式求出：

(54)

(55)

求解出期望控制输出后，需要根据无人机动力系统设计参数，对发动机推力和矢量喷口偏角进行限幅，再将控制信号输出给执行机构。第2级增量分配法的控制流程图如图7所示。基于增量的2级递进式优化控制分配方法避免了求解非线性方程组的迭代过程，并对优化变量采用合理的约束策略，可以大大加快求解速率。在无人机进行大机动飞行时，发动机控制量增量较大，此时(52)式中忽略的高阶小量会造成较大误差，因此这种增量分配法适用于机动幅度适中的航迹跟踪控制。在无人机6自由度过渡机动过程中，该控制分配方法的可行性及对大机动飞行的适用性，将在仿真分析中进行验证。

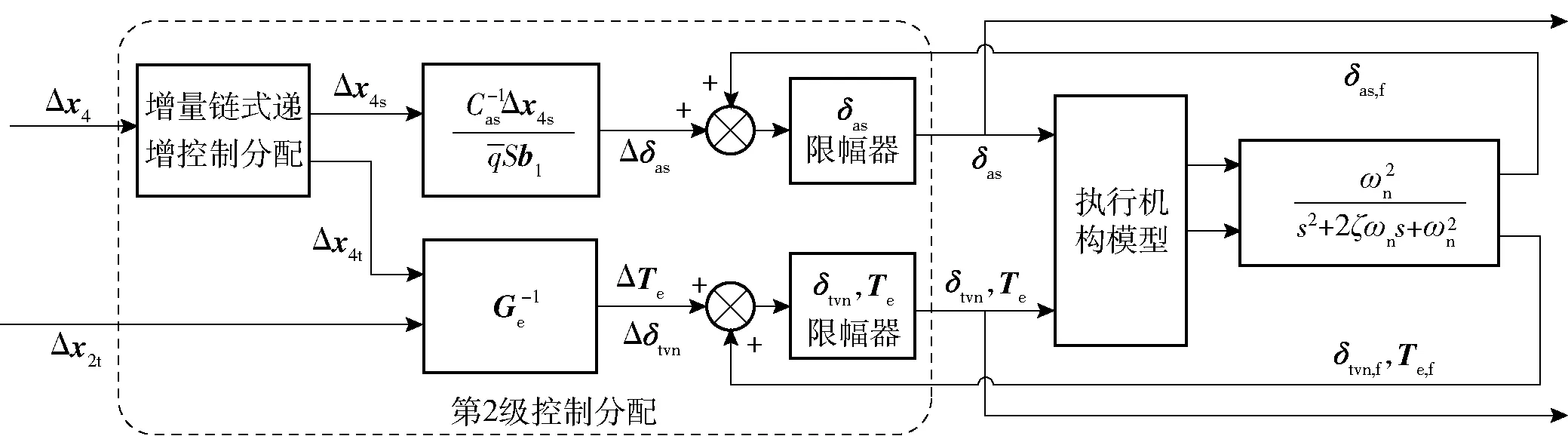
图7 第2级增量分配法的控制流程图Fig.7 Flow chart of second stage incremental control allocation

4 仿真分析

下面通过设计无人机6自由度过渡机动飞行算例验证本文所提出的控制方法。无人机目标航迹设计如(56)式所示：

(56)

无人机从悬停状态开始，在地面坐标系x轴方向做匀加速运动，在y轴方向做周期性侧向运动，在z轴方向先爬升高度后进行俯冲，参考航迹跟踪图和地面系速度对比图如图8和图9所示。本算例充分展现了无人机过渡飞行状态的6自由度机动特性。为了体现2级递进式控制分配能够适应不同的任务需求和飞行状态，共设计两种权值选取方案。方案1希望无人机在航迹跟踪过程中姿态变化幅度尽量小，多采用直接力控制进行航迹跟踪。这种机动方法适用于载人垂直起降飞行器过渡飞行。方案2希望无人机在航迹跟踪过程中较少地使用直接力，多采用姿态控制进行航迹跟踪。这种机动方法适用于小型无人飞行器过渡飞行。

图8～图15中的仿真结果显示，两个方案在0～10 s初始爬升阶段攻角α一直为负值(见图11)，且矢量喷口δl、δr下摆约90°(见图15)，升力风扇和推力矢量发动机共同工作(见图14)，无人机用推力补足升力进行爬升(见图13)。图13中由于机体坐标系z轴向下，Tz值取负。随着x轴方向速度以及俯仰角的增大(见图12)，两个方案的攻角逐渐增大。此时由不同权值选取方案造成的机动策略差异也逐渐体现。方案1在整个过渡机动过程中，攻角增速缓慢且姿态变化平稳，最大攻角α为22.3°，最大俯仰角θ为13.36°，升力风扇和推力矢量发动机一直在工作，为无人机提供直接力控制。方案2则相反，在过渡机动过程中攻角和姿态角变化明显，攻角α达到66.21°，俯仰角θ达到58.68°. 无人机采用大攻角飞行维持升力，升力风扇推力下降明显且在42～51 s时关闭。观察图8～图10可以发现，方案1的航迹跟踪性能比方案2好，这是因为方案2进行大攻角机动时气动非线性特性增强，给航迹跟踪控制加大了难度。

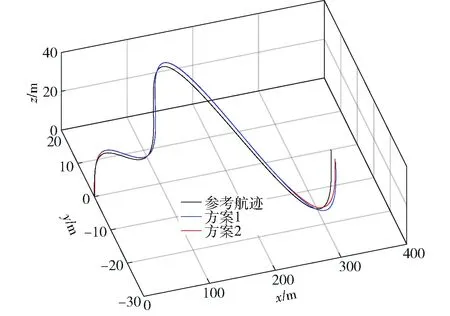
图8 航迹跟踪图Fig.8 Trajectory tracking

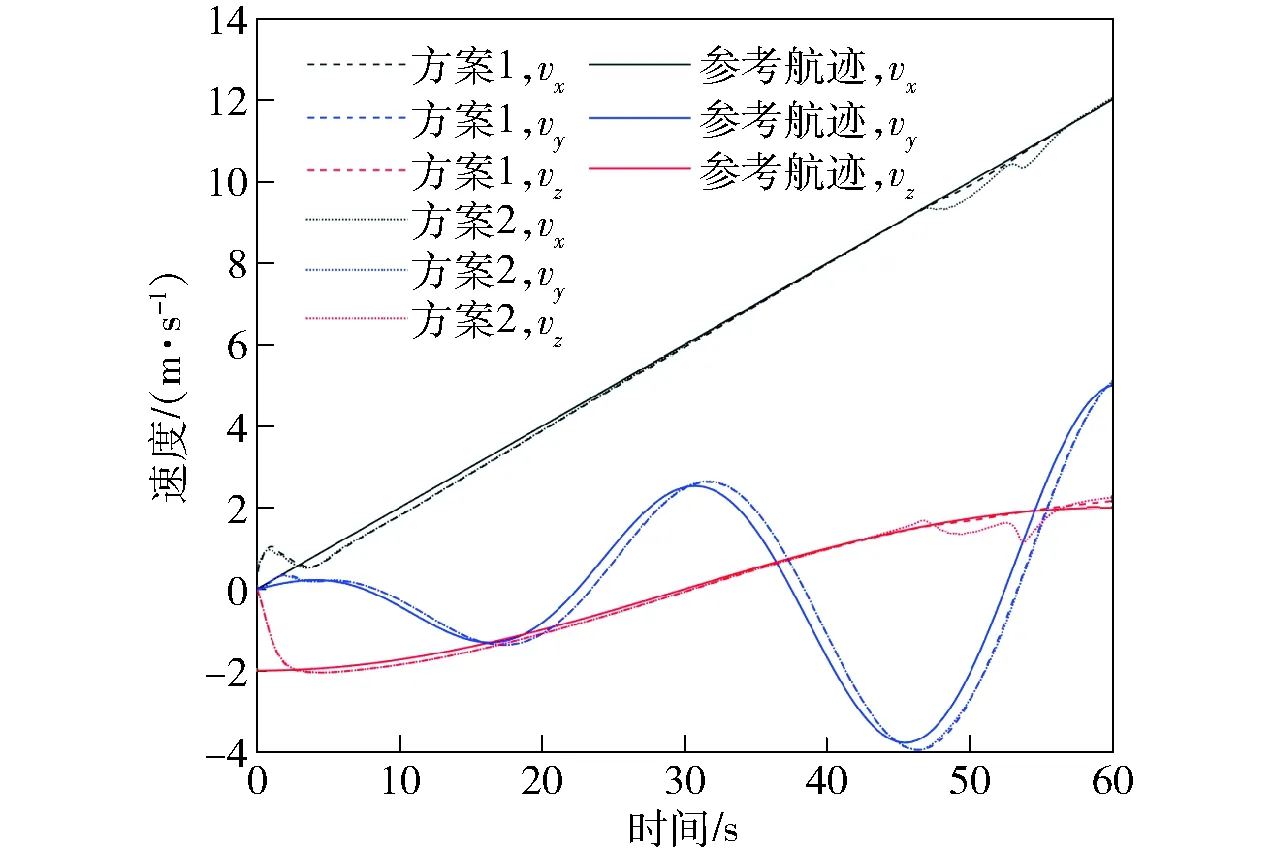
图9 地面系速度对比图Fig.9 Comparison of flight velocities in earth coordinate system

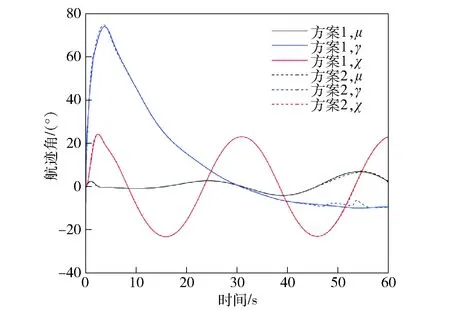
图10 航迹角对比图Fig.10 Comparison of flight-path angles

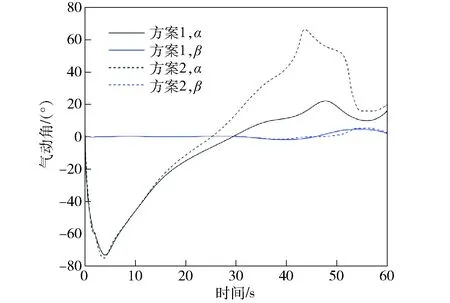
图11 气动角对比图Fig.11 Comparison of wind angles

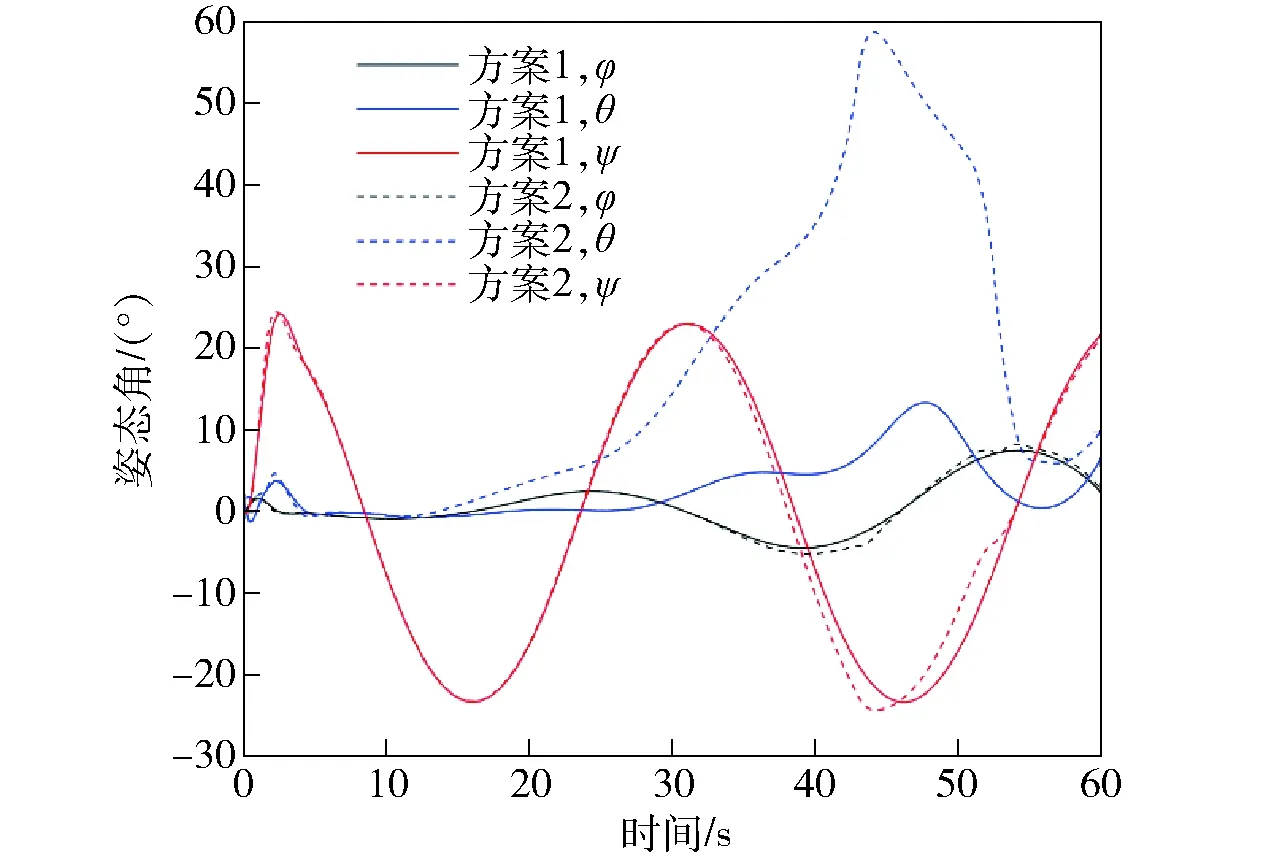
图12 姿态角对比图Fig.12 Comparison of attitude angles

图13 机体轴向推力矢量对比图Fig.13 Comparison of vectored thrusts in axial direction of airframe

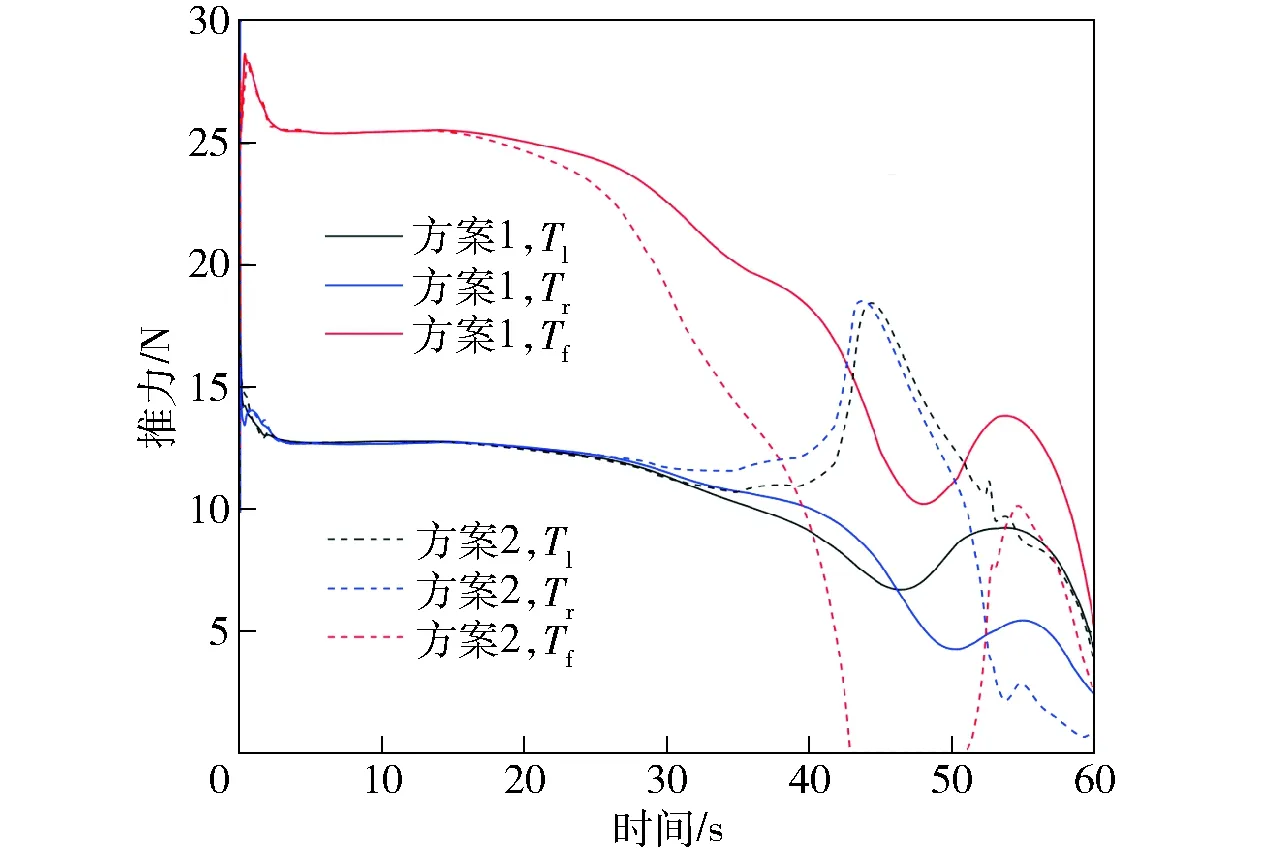
图14 发动机推力对比图Fig.14 Comparison of engine thrusts

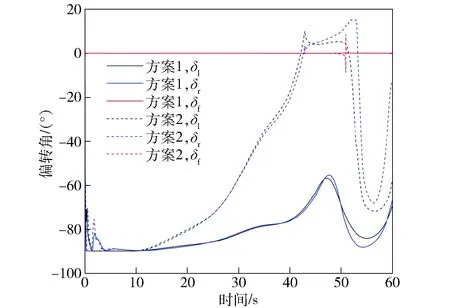
图15 矢量喷口及矢量舵偏转角对比图Fig.15 Comparison of vector nozzle and vector surface deflection angles

在40～60 s时无人机侧向机动幅度增大。图14中两种方案的左右矢量发动机推力Tl、Tr均出现明显的差动现象，图15中矢量喷口偏角也出现偏差，并且图11和图12中侧滑角β和滚转角φ的变化趋势一致。这些现象均表明在侧向机动过程中无人机采用侧滑转弯(STT)、倾斜转弯(BTT)复合控制，证明2级递进式优化控制分配方法能够根据飞行状态调整控制策略，而不是仅仅在侧向机动中使用单一的控制方式。

观察图11可以发现，随着速度增加，方案1和方案2的攻角先增大、后减小。这是因为在过渡机动前期通过增大攻角而提高了升力，从而可以明显地减小发动机推力，使(36)式中的目标函数取得更小的结果。当攻角超过一定范围时，增大攻角不会增加升力，升力风扇的推力降低，但是矢量发动机推力明显提升。此时增大攻角反而会使目标函数的结果增大，因此优化控制分配会在后期选择降低攻角。图中两个方案攻角开始下降时间的不同是由权值选取的差异造成的。

从图14可见，方案2的机动策略中无人机在42 s时关闭升力风扇，在51 s时又重新开启。产生这种机动决策的原因是在50 s后无人机跟踪目标航迹需要进行快速侧向机动，但是在大攻角状态下无人机动力系统无法提供足够的侧向机动力，因此控制系统通过降低攻角并重启升力风扇，利用滚转和偏航机动产生侧向力并改变机头指向，实现对侧向高机动航迹的跟踪。

以上机动策略都是2级递进式优化控制分配方法根据权值选取方案自动解算出的。仿真结果验证了本文提出的基于INDI优化控制分配方法的可行性，并展示了无人机具有的良好过渡机动控制性能。

为了分析控制器的抗扰动性能，在方案1基础上加入外界强扰动，同时选取NDI控制器作为对比算例，验证INDI方法应对气动不确定性的优势。由于NDI无法像INDI一样将控制方程写成增量形式进行解耦并线性化，针对采用直接力控制且具有控制冗余的飞行器，在第1级控制分配中采用SQP非线性优化方法求解[2]，在第2级优化控制分配中采用与本文类似的链式递增法求解，进而设置INDI和NDI控制器在每个回路的控制增益相等。在机体x轴、y轴、z轴向加入气动力扰动如(57)式所示：

Fd=6Rsin (0.05πt)，

(57)

式中：R为取值范围在0～3且采样周期为3 s的随机数，用于体现复杂环境下风场突变性扰动；sin(0.05πt)为周期为40 s的正弦函数，用于体现风场宏观周期性扰动。仿真结果如图16和图17所示。

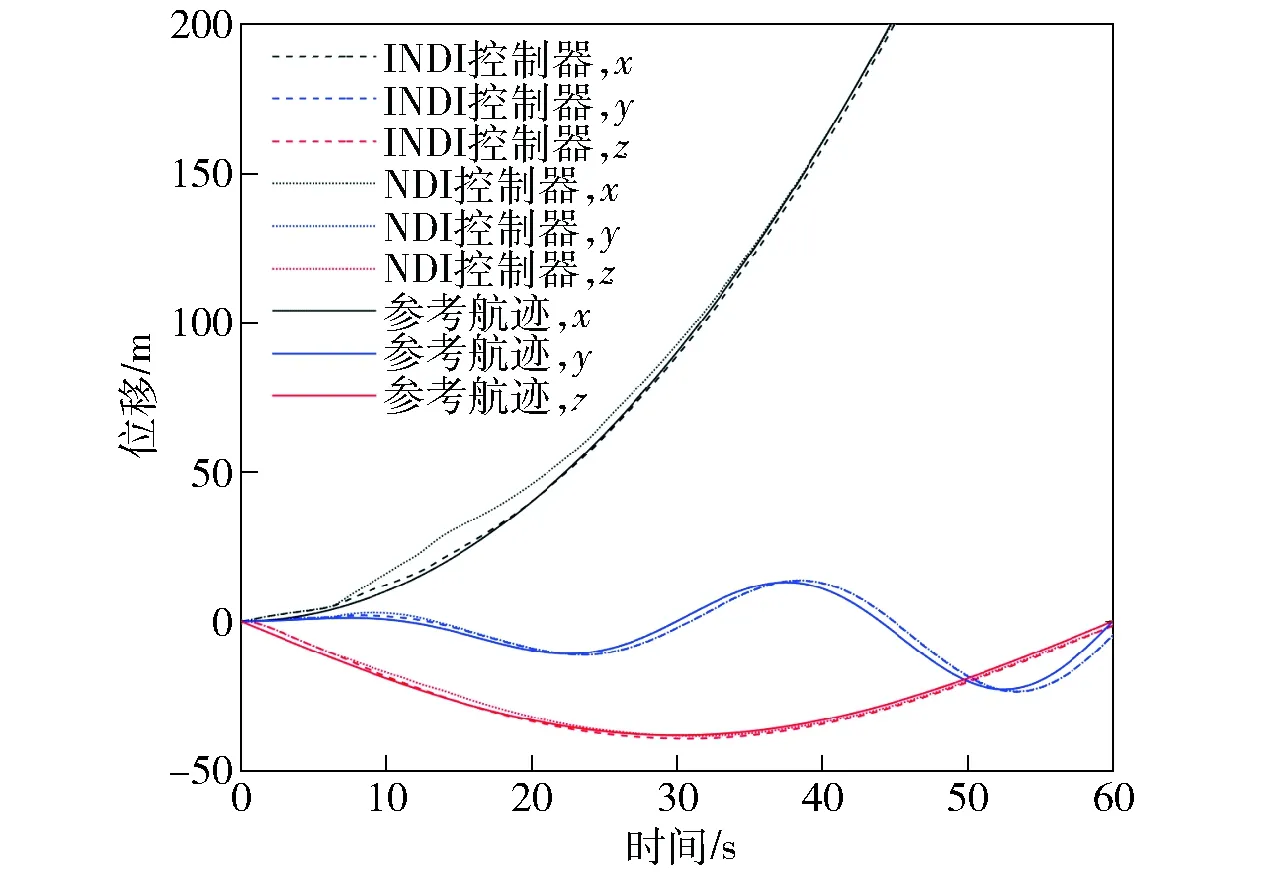
图16 加扰动时地面系下位移对比图Fig.16 Comparison of displacements in earth axis with disturbance

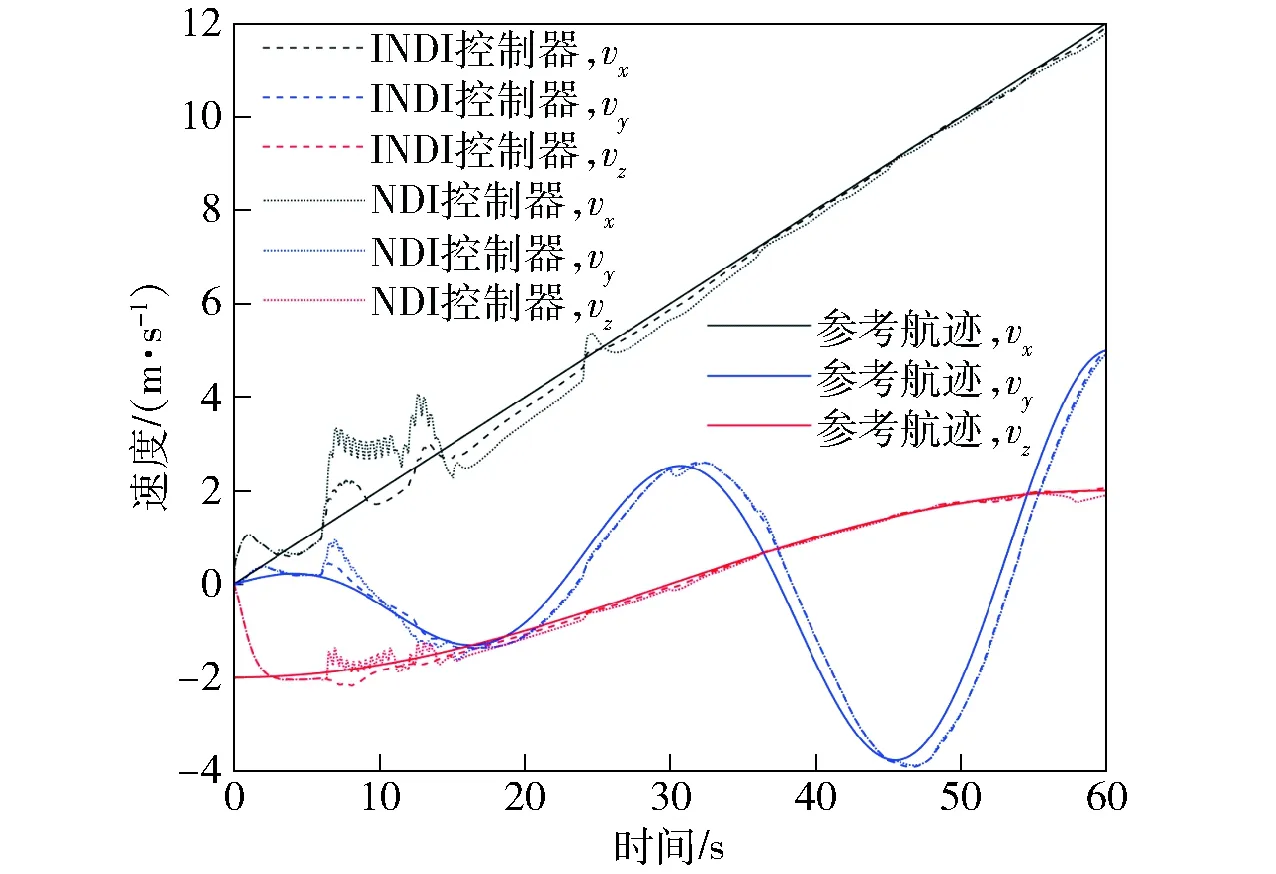
图17 加扰动时地面系下速度对比图Fig.17 Comparison of flight velocities in earth coordinate system with disturbance

观察图16和图17可以发现，在外加扰动情况下，INDI控制器和NDI控制器都能对目标航迹进行跟踪，但是INDI控制器与标准航迹位置和速度的偏差明显比NDI控制器小。在10 s左右Fd中正弦函数达到峰值，此时无人机处于过渡机动初始阶段，速度较低，主要靠直接控制力抵消外界扰动，因此速度波动明显。随着速度提升，无人机自身气动力作用增大，受扰动后可通过姿态微调和直接力共同抵御外界扰动，因此飞行速度增大后无人机航迹位置和速度受扰动影响较小。综上所述，INDI控制器抗外界扰动性能良好，在应对气动不确定性方面比NDI具有一定优势。