月球探测器着陆动响应区间不确定性分析

陈昭岳， 刘莉， 陈树霖， 崔颖

(北京理工大学 宇航学院 飞行器动力学与控制教育部重点实验室， 北京 100081)

0 引言

月球探测器成功软着陆是完成月球探测任务的重要条件。当探测器降落在月球表面时，对月球表面的撞击会形成较大的冲击，探测器携带的电子仪器设备能否经受得住这一冲击是软着陆能否成功的关键。探测器软着陆动力学分析对探测器结构和缓冲系统的设计具有重要指导意义。

只考虑确定参数的着陆过程动力学分析，国内外学者已进行了大量的工作[1-6]。探测器在实际着陆过程中的着陆速度、着陆姿态等都会存在不确定性，相对确定值存在区间波动，现有的文献对含不确定性因素探测器着陆过程的动力学响应分析较少，并且主要使用蒙特卡洛分析方法。Merchant等[7]将蒙特卡洛方法引入着陆动力学分析中，对“阿波罗”飞船登月舱的冲击载荷进行了不确定性分析。陈金宝等[8]以4腿“悬臂梁式”月球探测器为研究对象，对132种着陆工况进行仿真分析，研究了着陆姿态和着陆速度对探测器着陆性能的影响。

实际分析中，探测器着陆状态参数只能获得其不确定性区间边界信息，而区间方法适用于这类只含有边界信息的动力学问题。探测器模型庞大，结构复杂，具有强非线性特点，而目前常用的动力学区间分析方法如Taylor级数法[9-11]、Taylor模型法[12-15]计算过程复杂，且对于强非线性问题无法满足精度要求。基于Chebyshev多项式的区间分析方法可以有效地处理这类非线性问题，相对于传统Taylor方法，Chebyshev多项式方法在处理非线性问题时，能更有效地压缩区间算法的包裹效应，具有更高的求解精度和计算效率。Wu等[16-19]提出了利用Chebyshev多项式展开构造替代模型求解区间动力学问题，并将区间Chebyshev多项式分析方法应用于不确定条件下汽车悬架动态响应分析。Xia等[20]将Chebyshev多项式方法应用于不确定时域系统动态响应分析中。Li等[21]利用稀疏回归和Chebyshev多项式，提出了高效的非线性动力学系统区间响应分析方法。刘坚等[22]针对多层穿孔板超材料声学透射率分析，提出了一种区间Chebyshev展开——蒙特卡洛模拟分析方法，该方法在区间变量条件下，高效地分析多层穿孔板超材料声学透射率的传输不确定特性。陈剑等[23]应用Chebyshev区间方法求解汽车动力总成悬置系统的固有频率和解耦率随元件刚度值波动的范围。

本文在Abaqus计算机辅助工程(CAE)软件平台上建立了一个全柔性探测器软着陆非线性有限元模型，并计算探测器倾斜着陆工况下关键点的动力学响应。之后基于Chebyshev多项式方法，提出了不确定条件下探测器着陆动响应区间分析流程，对比分析了Chebyshev多项式方法与蒙特卡洛仿真分析方法分析结果。

1 基于Chebyshev多项式展开的探测器着陆动响应区间分析方法

1.1 Chebyshev多项式方法

根据Weierstrass逼近理论，任何在闭区间内连续的函数都可均匀地近似为多项式，并且达到所期望精度要求。

对于变量x的函数f(x)，其输入参数含有n个不确定性区间变量，且不确定区间范围分别为xi∈[ai,bi]，i=1，2，…，n，利用k阶Chebyshev多项式用于近似原始函数f(x)，以提高其近似精度。

原函数f(x)用n维k阶截断Chebyshev多项式近似表示为

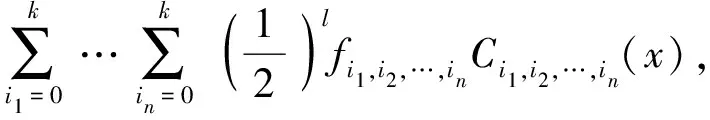
(1)

式中：l为n维Chebyshev级数Ci1,i2,…,in(x)的下标i1,i2,…,in中包含0的个数；Ci1,i2,…,in(x1,x2,…,xn)表示k阶Chebyshev级数，

Ci1,i2,…,in(x1,x2,…,xn)=cosi1θ1cosi2θ2…cosinθn，

(2)

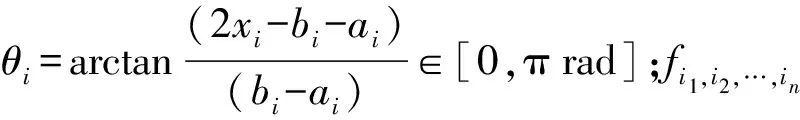
(3)

对(3)式采用Gauss-Chebyshev积分，可得

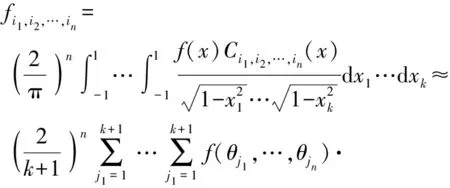
(4)

式中：θjk表示插值点，

(5)

m由多项式截断阶数k确定，一般取m=k+1.

如果函数f(x)具有k+1阶连续导数，则Chebyshev多项式与原始函数之间的近似误差为

(6)

将(1)式中的变量x替换为区间变量[x]，就得到了f(x)的Chebyshev多项式区间表示：

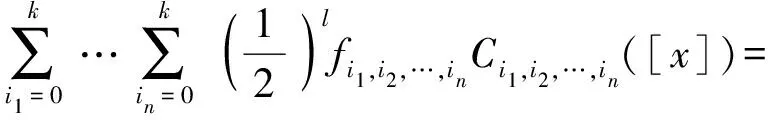
(7)

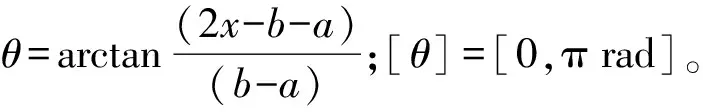
Ci1,i2,…,in([x])=
cosi1[θ]cosi2[θ]…cosin[θ]=[-1,1].

(8)

(7)式可进一步变换为

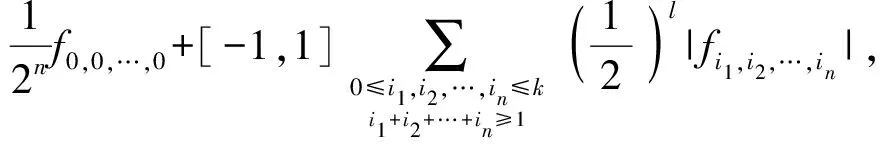
(9)

(9)式即为最终得到的区间上下界。

1.2 月球探测器仿真分析模型

本文在Abaqus/CAE平台上建立用于分析计算的全柔性探测器非线性分析模型。探测器模型主要由着陆器中心体、月球车、缓冲系统组成[24]。

中心体的主承力全部为复合材料夹层制成的板壳结构和起支撑作用的梁结构，所以建模为一个纯弹性的壳体和梁结构[25]；缓冲系统包括主着陆腿、辅着陆腿和足垫[26-27]，着陆腿外筒与中心体之间、辅着陆腿内筒与足垫之间的连接均设置为球铰。有效载荷(雷达、相机、桅杆和惯性组件等)的质量较小，将有效载荷的质量均匀分布到邻近的板壳结构上。

着陆腿由主缓冲腿和辅助缓冲腿组成，并采用筒式结构，其中铝蜂窝缓冲器嵌入缓冲腿中。根据参考文献[24]，结合实际情况，分别使用梁单元与壳单元对缓冲腿内外筒进行建模；着陆腿缓冲过程包含较强非线性，计算较为复杂，本文未考虑着陆腿缓冲载荷行程的参数不确定性，其缓冲载荷行程采用Abaqus连接器模型进行简化模拟，即主辅缓冲腿的载荷行程曲线简化成由弹性段和塑性段构成的理想化台阶模式。

月壤[28]建模为立方体实体模型，材料本构模型选择Cap Drucker-Prager模型用于分析。着陆冲击仿真有限元模型和响应点如图1所示。

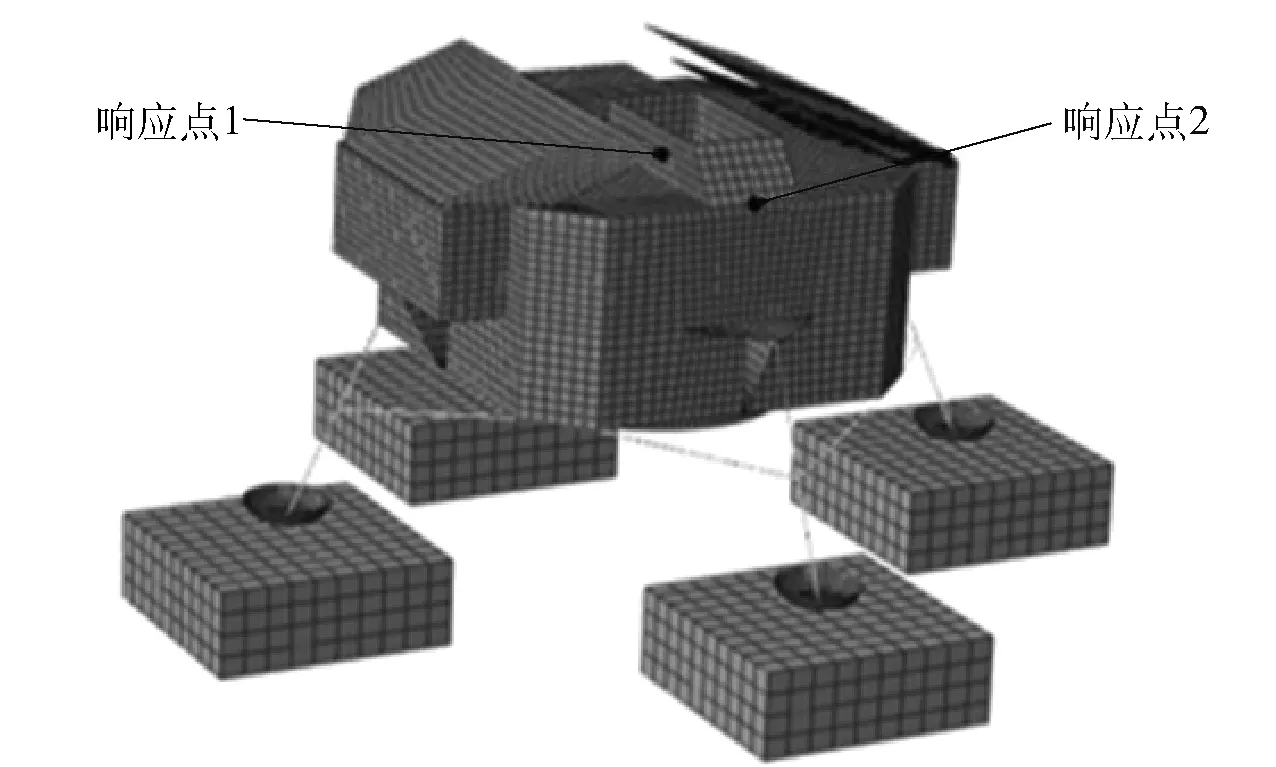
图1 探测器有限元分析模型Fig.1 Analysis model of lander

1.3 探测器着陆动响应Chebyshev多项式区间分析计算流程

探测器着陆过程的非线性反映在材料非线性和边界条件的非线性中，材料非线性指的是月球土壤材料以及缓冲支柱滑动副的弹塑性本构，非线性边界条件指的是足垫和月壤间的接触。

由于探测器的非线性特性，在软着陆动力学过程中每个时间增量步内都要重新计算整个系统的切线刚度矩阵，计算时间长且可重复性差。传统的区间分析方法，如Taylor级数法和Taylor模型法均为插入式方法，每一时刻需要单独调用求解器，并重新计算刚度、质量矩阵的偏导数，计算效率低。

Chebyshev区间分析是一种非插入式方法，无需重复调用求解器[16]，因此探测器着陆分析中利用Chebyshev方法可以利用有限元分析求解全过程着陆动响应，而不必每一时刻调用ODE求解器求解当前时刻响应，从而提高编程和计算效率。

本文基于探测器非线性着陆动力学分析模型和Chebyshev区间分析方法提出了探测器着陆动响应Chebyshev区间分析计算流程。采用Chebyshev区间多项式求解带有区间参数的探测器着陆动力学分析主要包括3个步骤：1)建立探测器非线性着陆动力学分析模型；2)输入不确定性参数和相应区间，进行参数插值，设定总仿真分析时间ttot，计算每个时刻当区间参数取值为插值点时，关键点动力学响应；3)计算每个时刻对应的Chebyshev系数，并构造Chebyshev区间多项式，利用区间算法计算解区间。

Chebyshev区间多项式求解带有区间参数的探测器着陆动力学分析的实现过程如图2所示。

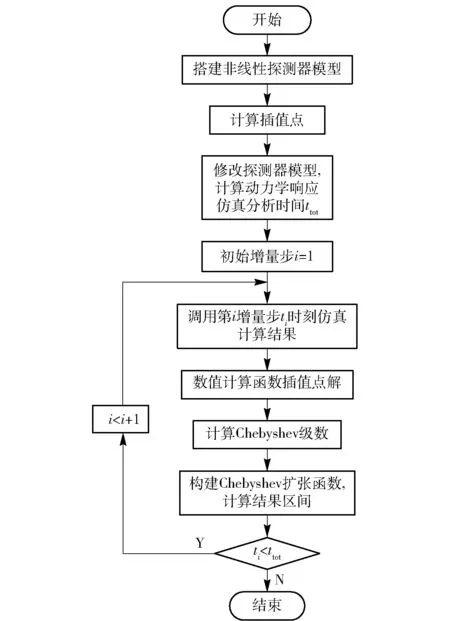
图2 Chebyshev模型法探测器动响应分析流程Fig.2 Flow chart of Chebyshev method for dynamic analysis of lander

2 月球探测器着陆动响应区间分析

2.1 探测器着陆分析工况确定

影响探测器着陆动响应的主要因素为探测器的着陆速度和着陆姿态倾角[3]。探测器着陆速度直接决定探测器的总动能，进而影响探测器动力学响应；着陆过程中着陆倾角有助于保持稳定性，不确定条件下的着陆倾角，对着陆时探测器受到不确定的冲击作用造成影响。

由于目前我国检评规范中的评价指标均采用百分制形式，为了与其它指标统一值域，故对横向裂缝状况指数TCCI进行百分化处理，以利于结合其他性能评价指标对路面性能进行综合评价。在此，采用“专家评分技术”，结合TCCI、TCS和TCL、TWR的发展规律分析结果，主客观相结合，对横向裂缝状况指数进行百分制处理。

为分析上述参数对着陆动力学响应的影响，本文考虑着陆姿态角和着陆速度的不确定性，参数区间中值分别设定为4 m/s(等价于地面试验中从0.87 m高处自由落体)和15°倾斜角，不确定性参数区间半径分别取5%和15%两种工况，对应小区间参数范围和较大区间参数范围。目前基于传统Taylor模型法的区间不确定性分析方法主要适用于区间半径在小不确定性区间的情况，而当不确定性区间较大时，传统方法需要将不确定性区间分割为数个小区间，分别求解响应结果区间，并进行区间集合，计算效率会显著降低。2种工况中的不确定性变量变化范围如表1所示。

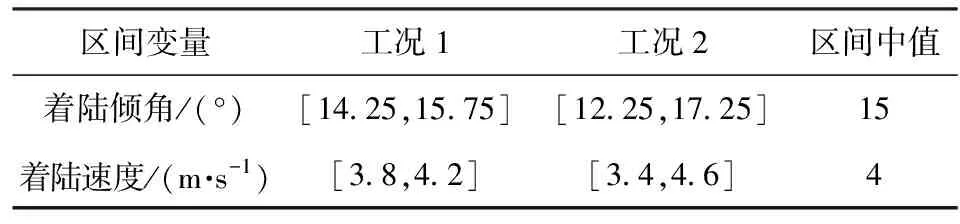
表1 不确定性变量区间范围

着陆动响应有限元分析步长选取0.5 ms，分析时间选取0.15 s，区间分析中使用4 阶Chebyshev级数。关键点选取探测器中心体的顶板中心点和太阳翼角点。分别利用Chebyshev多项式方法和蒙特卡洛仿真方法计算得到响应点的加速度响应区间，以蒙特卡洛方法得到的数据结果作为准确值。

蒙特卡洛分析中子样本数最少应在数百，本文中，蒙特卡洛分析中各变量的分布为均匀分布，子样数为400，可以认为子样数已足够。

2.2 探测器着陆动力学响应区间分析

在工况1 和工况2两种参数不确定区间条件下，考虑着陆姿态角和竖直着陆速度不确定性的探测器着陆动响应区间分析与蒙特卡洛分析结果分别如图3和图4所示。

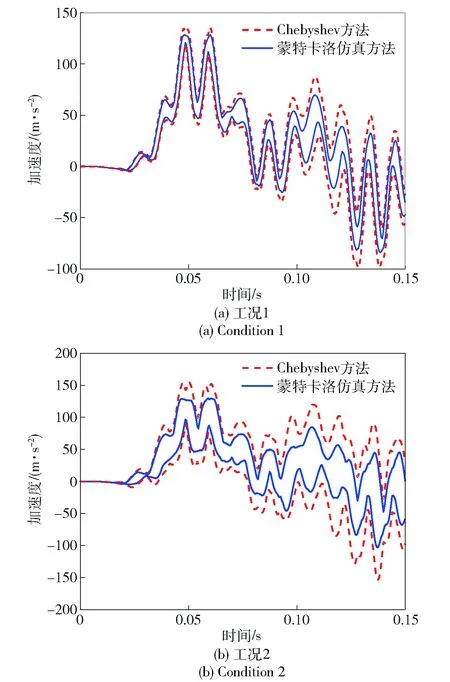
图3 测试点1不确定响应边界Fig.3 Interval bound of dynamic response of Point 1

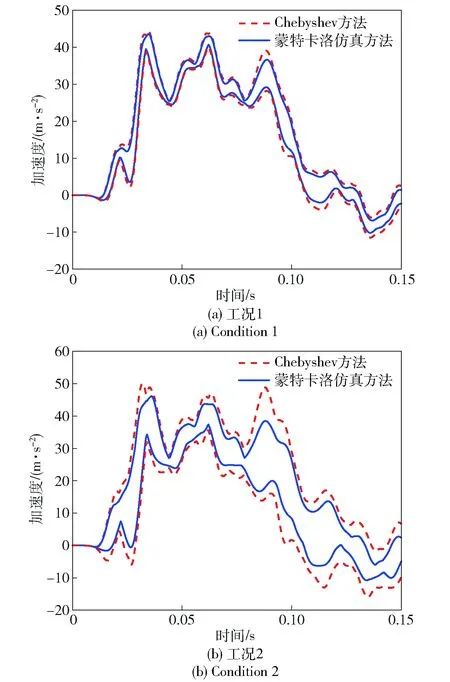
图4 测试点2不确定响应边界Fig.4 Interval bound of dynamic response of Point 2

月球探测器着陆动响应不确定性分析中，最关注的是探测器加速度峰值的不确定分析精度。在加速度峰值附近，工况1中Chebyshev区间动响应分析结果与蒙特卡洛分析结果最大相对误差为12%，工况2中最大相对误差为16.8%. 从中可以得出，采用Chebyshev模型分析得到的探测器着陆动力学响应区间上界、下界与蒙特卡洛分析得到的区间上界、下界基本吻合，通过Chebyshev 区间多项式方法获得的分析结果可以完全包含系统的真实解，且结果区间没有出现被过度放大的包裹效应，波动现象不强。

工况2中不确定性参数的区间半径超过15%，属于大不确定性区间问题，但采用Chebyshev模型法获得的区间结果仍能够完全包含系统的真实解，结果区间的波动现象并不剧烈，结果区间被放大的较少。

现有算法针对大不确定性问题，均会出现一定程度的计算误差增大，属于各区间算法固有的缺点，本算法当区间半径超过15%时，最大相对误差为16.8%，仍保留较高的计算精确度。

2.3 Chebyshev模型截断阶数影响分析

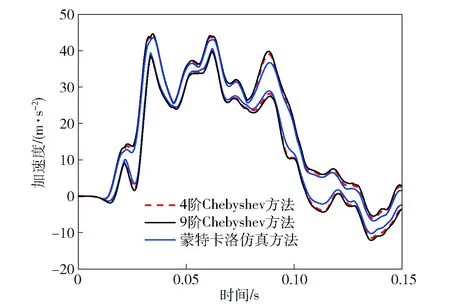
图5 测试点1不确定响应结果对比Fig.5 Comparison of interval bounds of dynamic response of Point 1

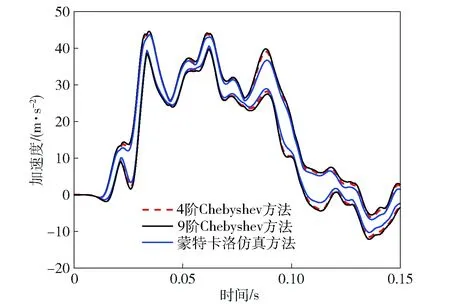
图6 测试点2不确定响应结果对比Fig.6 Comparison of interval bounds of dynamic response of Point 2

由图5分析对比结果：当k=4时，Chebyshev方法得到的区间响应上界和下界可以包络蒙特卡洛方法求得响应边界，且结果的最大相对误差为15%；k=4和k=9时求得的区间响应上界和下界非常接近，最大相对误差小于5%，证明本文选取的截断阶数为4，满足计算精度的要求。

Chebyshev多项式的近似误差可以表示为

随着多项式阶数k的增大，Chebyshev方法的误差项ek(f)将迅速减小，因此当选取足够大阶数k时，本方法的分析误差可忽略。本节分别选取4阶和9阶Chebyshev进行分析，由误差表达式可以看出，k取4阶和9阶时，近似误差均已足够小，因此本算例中阶数对分析误差影响可以忽略。

探测器单次着陆仿真所需时间约40 min，构建Chebyshev模型所用时间相对于仿真时间可以忽略不计。

根据算例分析结果，对于低阶问题，采用构造较低阶数的Chebyshev多项式的方法，如本文构造4阶Chebyshev多项式，已满足精度要求。本文算例构造的Chebyshev多项式仅需要采样调用有限元模型进行25次仿真计算，计算成本很小。与之对比，蒙特卡洛方法通常需要至少进行数百次的分析，在本算例中，蒙特卡洛方法的子样本数为400；两种分析方法结果误差不超过15%，而Chebyshev方法的采样数比蒙特卡洛方法小一个数量级，因此有更高的计算效率。

值得注意的是，随着时间步的推进，Chebyshev区间多项式方法的区间参数预测结果误差有放大现象，并且多维区间参数下计算次数仍然呈指数型增加，因此不建议在长时间、多维区间参数动力学仿真分析中使用。

3 结论

1)本文构建月球探测器着陆动力学模型，并基于Chebyshev多项式理论，提出了探测器着陆动响应Chebyshev区间分析计算流程，可用于不确定条件下的探测器着陆动响应分析。首先构建月球探测器着陆动力学模型，然后根据输入的不确定性参数和相应区间进行参数插值，计算每个时刻当区间参数取值为插值点时，关心点的动力学学响应，利用截断Chebyshev多项式方法计算探测器动力学响应区间结果。

2)采用Chebyshev区间计算方法与蒙特卡洛仿真分析方法对月球探测器着陆动力学响应进行对比分析，结果表明，与蒙特卡洛方法相比，Chebyshev区间方法可以准确、高效地得到探测器着陆动响应上界和下界，区间结果能够完全包含系统的真实解，结果区间的波动现象并不剧烈，结果区间被放大的较少。对Chebyshev区间方法中多项式级数的选择进行分析，结果表明恰当的多项式阶数选取不仅使分析得到的区间结果满足精度要求，且结果区间放大较小。