状态自适应无迹卡尔曼滤波算法及其在水下机动目标跟踪中的应用

马艳， 刘小东

(1.西北工业大学 航海学院， 陕西 西安 710072； 2.中国舰船研究设计中心， 湖北 武汉 430061)

0 引言

水下对抗中，不仅要快速跟踪机动目标，而且要准确估计目标非机动时刻的航速与航向。水下主动探测平台通常提供的观测量有目标距离和方位，由于背景噪声的存在，探测平台估计的目标距离和方位不可避免地与真值之间存在偏差，误差大小与信噪比呈反比。在目标跟踪中，通常以目标的位置矢量和速度矢量作为状态向量，观测方程中目标方位与位置矢量为三角函数关系，因此其观测方程具有很强的非线性。

对于非线性目标跟踪，传统卡尔曼滤波器(KF)将不再适用，常用的非线性目标跟踪算法主要有扩展卡尔曼滤波(EKF)[1-3]、无迹卡尔曼滤波(UKF)和粒子滤波(PF)。其中：EKF是一种线性化处理方法，通过泰勒展开去除高阶项影响，对于强非线性水下的目标观测方程将会带来较大误差；PF是基于Monte Carlo方法的重采样滤波算法[4-5]，无需考虑系统的概率密度分布，对非线性具有良好的适应性，但存在计算量大、面临粒子退化等缺点；UKF是基于无迹技术(UT)的KF，该方法首先对非线性函数的概率密度分布进行近似[6-7]，无需考虑状态方程和观测方程的线性化处理，对于强非线性系统有着良好的滤波效果[8-9]。UKF算法在进行目标跟踪时需要提前建立目标的状态方程，即固定状态噪声，但是在目标机动时，目标运动状态与状态方程并不能实时完全匹配，从而带来较大的状态噪声。若依然采用传统UKF算法，则可能会导致跟踪精度降低甚至发散等问题。

针对UKF在跟踪机动目标面临的问题，学者们提出了一些UKF的改进算法[10-14]，具有代表性的有Sage-Husa算法及其改进算法。Sage-Husa是一种次优无偏极大后验估计器，在滤波过程中不断调整状态噪声方差阵，但在更新过程中会出现负定的噪声方差阵，从而导致滤波中断。为了使UKF适应跟踪过程噪声的变化，赵治国等[10]将改进的自适应Sage-Husa算法与UKF结合，在线更新噪声的统计特性。石勇等[12]提出一种基于协方差匹配的方法来抑制滤波发散，通过调整预测协方差的系数改变其在滤波过程中所占的权值，但该方法易破坏滤波过程的稳定性，目标强机动情况下也出现滤波发散的情况。周卫东等[13]提出一种基于新息和残差的自适应UKF算法，但该方法在滤波过程中对观测方程进行泰勒展开的线性化处理，带来了较大误差。陈政等[14]提出采用最大期望算法(EM)估计的过程噪声参数，改善UKF不能适应统计特性未知的非高斯过程噪声时性能，但过程噪声参数估计复杂。上述算法充分考虑了滤波的快速跟踪性，但没有考虑跟踪结果的平滑性，对于目标非机动情况下速度与航向的预测准确性不高。

本文针对水下机动目标实时跟踪和准确估计目标航速和航向问题，提出一种目标状态噪声方差随残差概率分布自适应调整的UKF方法，避免了Sage-Husa算法中出现负定噪声方差阵的问题，同时避免了线性化带来的误差问题。仿真结果表明，该方法不仅能得出比传统UKF更加精确的滤波效果，而且能迅速得到平滑的滤波曲线，具有较高的航速和航向估计精度。

1 状态方程以及观测方程

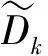
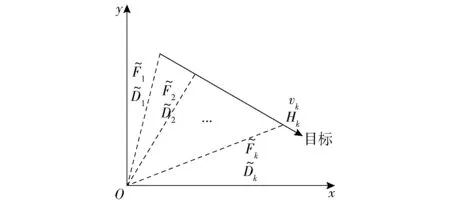
图1 观测模型Fig.1 Observation model

在所建立的二维直角坐标系中，该跟踪系统的状态方程、观测方程和目标运动要素方程分别为

(1)

(2)

(3)

式中：t为采样间隔；wk为状态噪声，服从N(0,Qk)的高斯分布，Qk为非负定矩阵；uk为观测噪声，服从N(0,Rk)的高斯分布，Rk为正定矩阵；uk与wk相互独立。观察(2)式可知，跟踪系统的状态方程、观测方程和目标运动要素方程是明显的非线性方程。

2 UKF基本原理

UKF基本原理是以UT变换为基础，采用KF框架和确定性采样形式，在减少采样粒子点数的同时保证逼近精度。UKF算法可分为初始化、UT变换、时间传播方程和测量更新方程4个步骤[6-7]：

1)初始化。

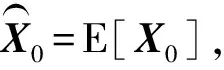
2)UT变换。

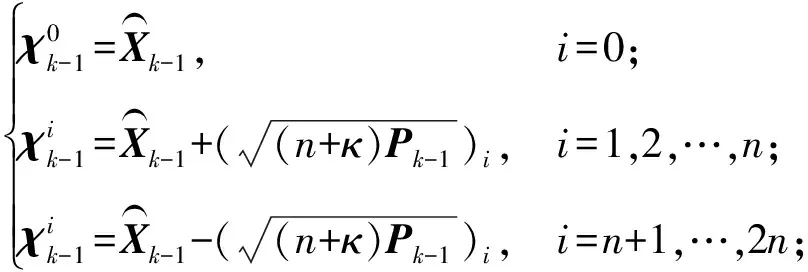
3)时间传播方程。

4)测量更新方程。

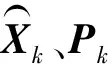
3 基于残差概率分布的自适应UKF

水下目标运动通常分为匀速直线巡航与机动两种状态。对于做匀速直线巡航的目标而言，对于(1)式所示的状态方程，其所对应目标的运动模型是完全准确的，在滤波初始值误差不大情况下，此时状态噪声方差Q是很小的，若此时给定Q较大的值，则在步骤2～步骤4迭代过程中，由于误差积累，使得滤波协方差PX增加[14]，即误差波动较大，滤波结果更依赖于观测值，即预测值权重减小。虽然滤波算法可以收敛至真实值附近，但滤波结果的起伏较大，曲线不光滑，由(3)式不能准确估计目标的航速和航向；而在目标机动时，目标航速在不断变化，(1)式状态方程将是变化的，此时若Q取值过小，将会使滤波器无法跟踪到目标的机动，进而使滤波结果发散。

在实际目标跟踪过程中，目标运动状态是未知的，为了同时兼顾跟踪机动目标速度和稳定状态时的跟踪精度，需要对目标状态进行实时监测，即在目标出现机动时取较大的Q值，在目标匀速巡航时取较小的Q值。

3.1 滤波发散的判决条件

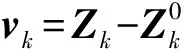
(4)

(5)

(5)式即为判决滤波发散趋势的判决条件。在不满足该条件时，判定滤波发散，即目标处于机动状态，需要调整状态噪声方差Q.

3.2 实际参数选取

如(5)式所示，判决条件为残差概率，因此在实际滤波过程中，计算残差概率需要先做统计。设定一个宽度为N的判定窗口，在滤波初始阶段：当数据长度小于等于N时，按照常规KF来计算；当数据长度大于N时，计算窗口内残差的概率分布：

(6)

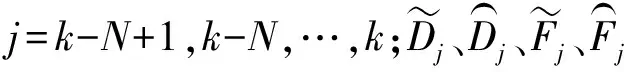
由于数据长度N不是无限长，即使预测值与真值完全相等，也很难得到(5)式结果，因此再设定一个容错门限η：

(7)

即当预测值和观测值残差大于0的概率偏离0.5较远(>η)时，判定目标正在进行机动，否则认为目标处于匀速巡航状态。η取值范围为(0，1/2)，η值越小，预测值和观测值微小的差别即可体现，系统对目标机动情况下的跟踪能力越强，但稳态时，滤波曲线的平滑程度将降低；η值越大，系统对目标机动情况下的跟踪能力减弱，但滤波曲线的平滑程度将增加。

当(7)式成立时，表明此时目标在进行机动，滤波结果已发散，对状态噪声方差做如下处理：Qk=Qk-1+λ(λ为状态变化量)，对于(1)式所示的状态方程，目标位置变化过程始终是正确的，产生误差的主要原因是速度变化过程。现阶段能够做强机动的水下目标速度变化率通常不会很大，在此取λ=diag(0, 0, 0.1, 0.1)，用来调整状态噪声方差，使其迅速增加，以减少预测值在滤波过程中的权重，从而抑制滤波结果的发散。

当(7)式不成立时，表明此时目标没有进行机动，且滤波结果收敛到真值附近，为了得到更加平滑的滤波结果，对状态方差做如下处理：Qk=γQk-1,其中γ=diag(1,1,1/(k-1),1/(k-1))为衰减系数矩阵，用来使状态噪声方差迅速减小，增加预测值在滤波过程中的权重，使结果更加平滑。

从调整的过程看，虽然Q值在滤波算法发散时增加，而在滤波算法收敛时减小，但是始终是大于0的，因此不会出现滤波算法中断的情形，弥补了Sage-Husa算法的不足。

4 数值仿真

为了验证基于残差概率分布的自适应UKF算法的有效性和性能，进行数值仿真：与传统UKF算法进行对比，以验证算法的有效性；分析测量方差、机动性强弱(转弯角度)以及容错门限对算法性能的影响。对每个仿真条件进行100次Monte Carlo实验，计算各个观测点滤波结果的均方根误差(RMSE)。为了评价目标匀速运动时估计的航速和航向的稳态值，取目标机动前(200～1 000 s)以及机动后(1 200～2 000 s)时间段内目标速度与航向的统计特性，即RMSE均值和误差标准差的均值，如(8)式和(9)式，RMSE均值用来验证滤波结果的准确性，标准差均值用来验证滤波曲线的平滑性。

(8)

(9)

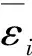
通过收敛时间评价算法对机动目标的跟踪性能，定义滤波结果的RMSE大于观测结果的RMSE时为发散时刻点t1，相应地，滤波结果的RMSE小于观测结果的RMSE时为时刻点t2，则在目标机动时滤波的收敛时间为t2-t1.

4.1 仿真实例

目标运动轨迹和目标位置估计的RMSE分别如图2和图3所示，目标速度与航向估计的统计特性如表1所示。从图3和表1中可以看出：对于Qa,即较大的状态噪声方差情况，其位置估计结果相对平稳(尤其是1 000 s处)，对目标机动状态的适应性较强，但其在稳态时滤波估计误差很大，尤其是目标航向，这不利于目标的前向预测；对于Qb，即较小的状态噪声方差情况，当目标匀速直线运动时(机动前)，其位置估计结果误差较小，但在目标做机动后其收敛速度很慢；而状态自适应UKF算法虽然在目标机动时其位置误差明显增加，但在判断滤波结果发散情况下能迅速收敛至真值附近，避免了Qb情况所带来的滤波结果发散问题，同时在目标匀速运动时状态自适应UKF算法滤波结果误差最小，滤波曲线相对平滑，从而可以准确估计目标的航速与航向。

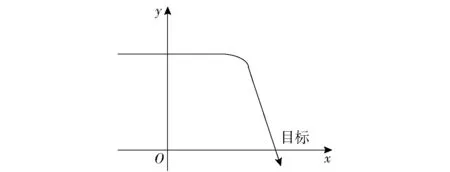
图2 目标运动轨迹Fig.2 Target motion trail

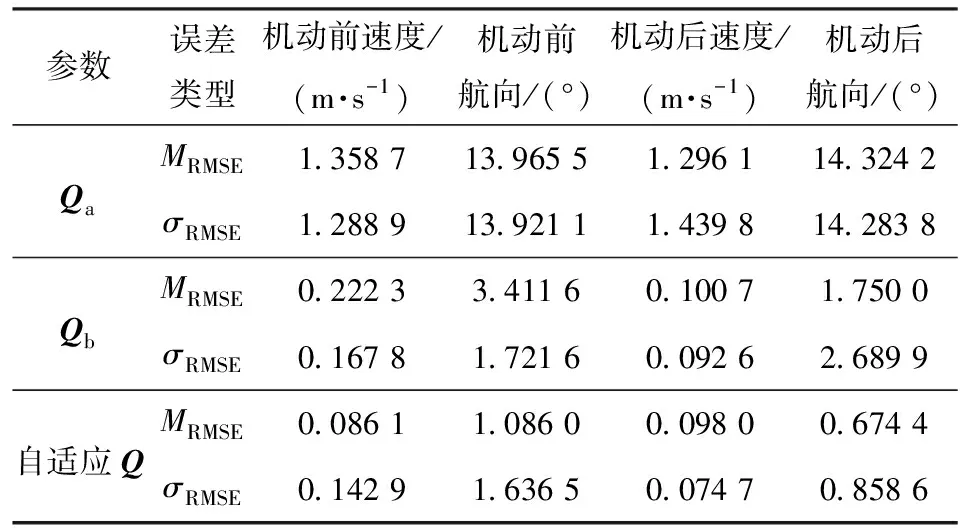
参数误差类型机动前速度/(m·s-1)机动前航向/(°)机动后速度/(m·s-1)机动后航向/(°)QaMRMSE1.358 713.965 51.296 114.324 2σRMSE1.288 913.921 11.439 814.283 8QbMRMSE0.222 33.411 60.100 71.750 0σRMSE0.167 81.721 60.092 62.689 9自适应QMRMSE0.086 11.086 00.098 00.674 4σRMSE0.142 91.636 5 0.074 70.858 6

4.2 算法性能

在4.1节仿真条件基础上，分别改变测量方差(距离和方位)、机动角度(机动性)和容错误差，每个条件下进行100次Monte Carlo实验，计算状态自适应UKF算法的滤波收敛时间、机动后的速度，航向的RMSE均值与标准差均值。

4.2.1 测量方差的影响

假设探测系统的距离标准差分别为20 m、50 m和80 m，方位标准差保持不变，为1°；或者方位标准差分别取1°、2°和3°，距离方差保持不变，为50 m. 算法性能如表2所示。从表2中可以看出：不同距离与方位噪声的增加会导致对滤波结果误差略微增加，对滤波性能影响不是很明显，在不同噪声条件下，系统均能计算出较为平稳、误差较小的结果。

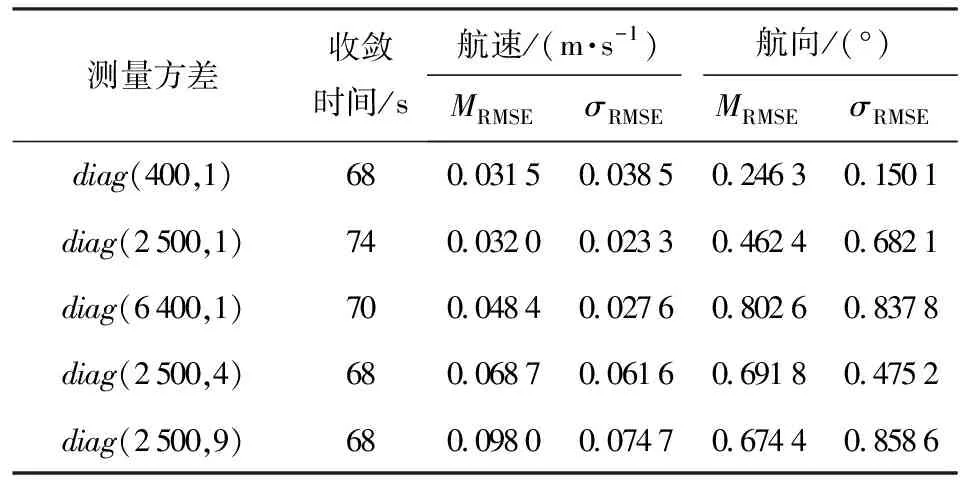
表2 测量方差的影响

4.2.2 机动性的影响

目标初始航向为90°，机动后的航向分别取135°、-135°和-90°，其他参数的选取与4.1节中相同，目标机动后算法的收敛时间、航速和航向的RMSE和标准差如表3所示。从表3中可以看出，转向角度大小对性能影响不大，表明该算法可以适应不同的机动转向。

4.2.3 容错门限的影响

从第3节的容错门限的定义可以看出：容错门限的范围在(0，0.5)范围内，容错门限越小，算法对目标机动越敏感，算法跟踪机动目标的能力越强；反之，算法跟踪机动目标的能力越弱，但滤波后曲线越平滑(误差越小)。保持其他参数不变，容错门限分别取0.2、0.3、0.4，算法的性能如表4所示。从表4中可以看出，本文算法跟踪机动目标的能力和平滑度与理论结果基本一致(由于这是统计结果，偶尔会有差别，如航速标准差)。

表3 机动性(转弯角度)的影响

表4 容错门限的影响

综合表2～表4可以看出，虽然改变了测量方差、目标机动性和容错门限，但是算法的收敛时间均在100 s以内，且平稳后算法估计的航速和航向误差较小，具有较好的适应性。

5 声纳信息综合处理系统

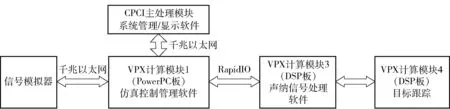
图4 声纳仿真系统框图Fig.4 Block diagram of sonar simulation system

为了验证状态自适应UKF跟踪算法在实际系统中的跟踪性能，将该算法应用于声纳信息综合处理系统算例。该算例是为了检验多功能标准台D系列嵌入式综合处理机平台能否适应声纳信号处理和综合分析能力设计的。系统由外围的信号模拟器、声纳信号处理模块、目标跟踪模块和显示模块等组成，如图4所示，后面3个模块将模拟真实的声纳信息处理过程。其中声纳信号处理包含主动和被动两种模式，可以完成主动探测中的波束形成、正交解调、信号检测、目标距离和方位估计，由于该算法只是模拟声纳处理过程，其目标距离和方位估计方法分别为谱值最大法和三波束定向法，算法简单，但误差较大。

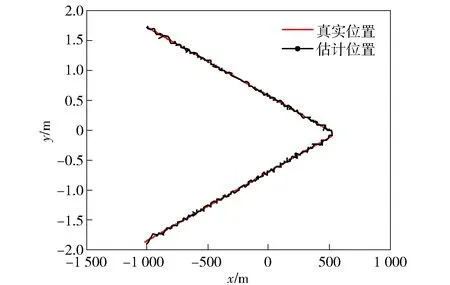
图5 目标运动轨迹和估计位置Fig.5 Target motion trail vs. estimated location

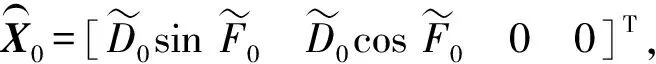
图6为跟踪的目标运动轨迹和目标位置估计的RMSE，该结果与第4节中理论仿真结果一致。如果状态噪声方差取得较大，则估计结果平稳，但是稳态误差较大；如果状态噪声方差取得较小，则UKF算法不能很快地跟踪目标机动，而状态自适应UKF算法则很好地兼顾了机动时的快速跟踪和匀速运动时的稳态误差。

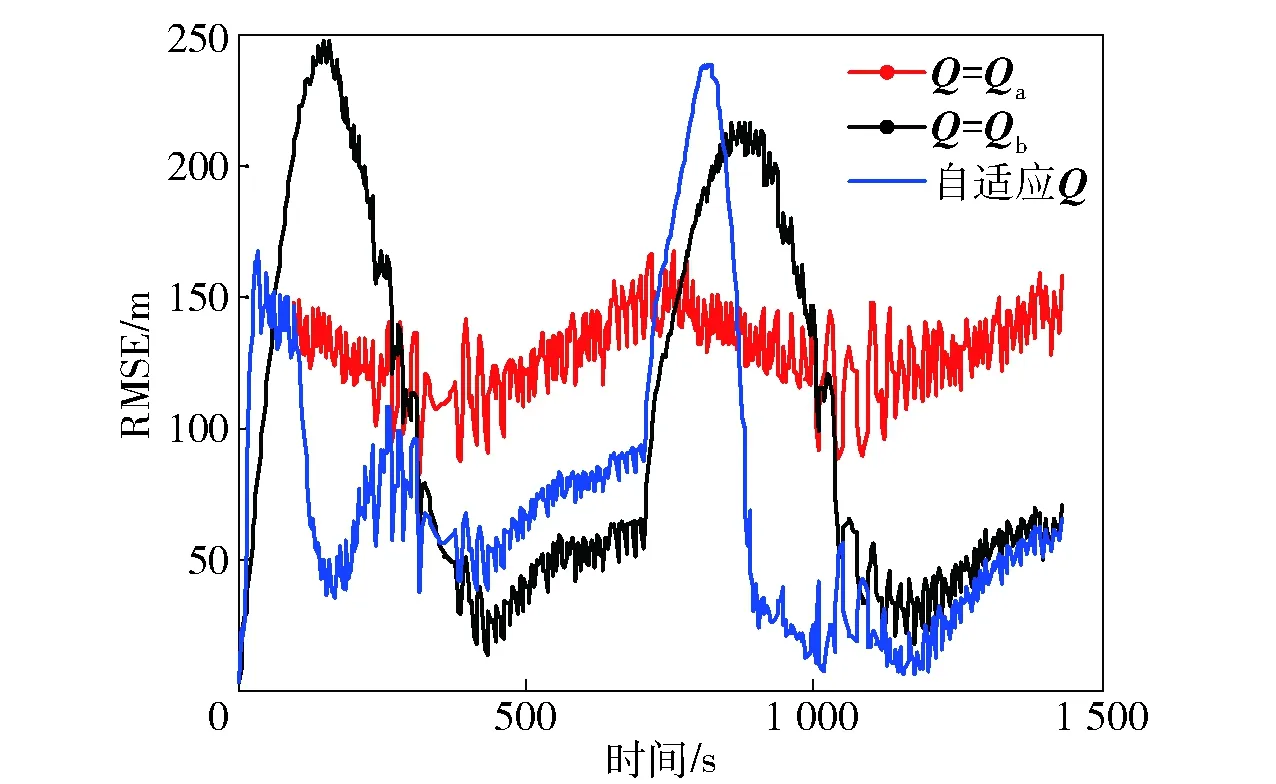
图6 目标运动轨迹跟踪的RMSEFig.6 RMSEs of tracking the target motion trail

6 结论

本文为了能够及时、准确地跟踪水下机动目标，对UKF算法进行了改进。以状态残差为标准，自适应地调整状态噪声的方差，使算法更加适应目标的机动。通过实验验证了该算法的有效性和测量误差、机动性和容错门限对算法性能的影响。结果表明：相对于传统UKF目标跟踪，该算法不仅能够准确地对机动目标进行跟踪，而且能够准确地估计出目标的航速与航向，进而准确地预测出其准确的前向位置，在水下对抗中有着重要意义。