改进的多扩展目标PHD滤波算法*
2019-03-12彭聪王杰贵朱克凡程泽新
彭聪,王杰贵,朱克凡,程泽新
(国防科技大学 电子对抗学院,安徽 合肥 230037)
0 引言
传统的目标跟踪中一般将运动物体视为点目标,此时只考虑目标的运动信息,而忽略了目标的外形信息。随着传感器技术的提升,新型的传感器可提供目标的多个量测值,这种在同一时刻能够得到至少一个量测值的目标称为扩展目标[1]。扩展目标不仅提供了目标的运动状态,还提供了运动体的外形信息(大小、形状和朝向等)。
基于数据关联的多目标跟踪算法一直是人们解决多目标跟踪问题的一个途径,但是这类算法会带来“组合爆炸”的问题[2],计算量庞大是这类算法的一个缺陷。2007年,Mahler在文献[3]中提出了随机有限集(random finite set,RFS)框架下的多目标跟踪方法,该方法将所有的目标状态和量测集看作随机有限集,然后通过多目标贝叶斯滤波计算同时估计出目标的个数和状态。由于算法中存在集值积分,求解十分困难,因此很多近似的滤波方法被提出,概率假设密度(probability hypothesized density,PHD)滤波器便是其中之一,它传递的目标概率密度的一阶统计近似矩。2009年,Mahler在Giholm和Sallmond给出的非均匀泊松点过程的目标量测模型的基础上,将PHD滤波技术应用于扩展目标,进行了扩展目标PHD(extended target PHD,ET-PHD)滤波的数学推导,给出了扩展目标PHD滤波器的更新方程[4]。2010年,Granstrom等学者给出了ET-PHD的高斯混合(Gauss mixture,GM)实现形式,即ET-GM-PHD滤波[5]。
量测集的划分是多扩展目标跟踪中的一个重要环节,2010年,Granstrom等人提出了一种基于距离阈值的划分方法,该方法适用于目标距离较远且量测密度相近的情况[6];文献[7]提出了k-means划分方法,其跟踪精度好于距离划分,上述2种方法都是基于距离计算的,对于量测密度差别较大的情况,两者划分效果较差。针对这种情况,2015年,文献[8]提出了一种基于SNN相似度的划分方法,该方法在目标产生量测密度差异较大的情况下划分效果较好,但存在计算量偏大的不足。
本文在文献[8]的基础上,提出了一种改进的ET-GM-PHD滤波算法,该算法首先通过LOF(local outlier factor)离群检测进行杂波滤除;然后根据SNN(shared nearest neighbor)相似度对预处理后的量测数据进行划分,从而达到缩短计算时间,提高跟踪稳定性的效果。
1ET-GM-PHD滤波算法
1.1 ET-PHD滤波算法
2009年,Mahler在文献[9]中将PHD滤波器推广到了扩展目标跟踪领域,并给出了数学推导:
(1) 预测部分
设k-1时刻的后验强度vk-1,则ET-PHD预测强度为
βk|k-1(xk|xk-1)]vk-1(xk-1)dxk-1,
(1)
式中:γk(xk)为k时刻新生目标的RFS的强度函数;pS,k(xk-1)为目标在k时刻存活的概率;fk|k-1(xk|xk-1)为k时刻单目标的转移概率密度;βk|k-1(xk|xk-1)为衍生目标的强度。
(2) 更新部分
设k时刻的预测强度vk|k-1(x)和量测集Zk,且量测个数服从Poisson分布,ET-PHD更新方程为
vk(x)=LZ(x)vk|k-1(x),
(2)
式中:LZ(x)为量测的伪似然函数,
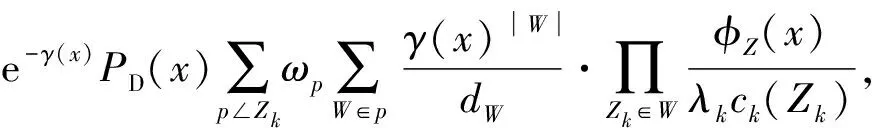
(3)
式中:γ(·)为扩展目标所产生的量测值的均值;PD(·)为目标被检测概率;p∠Zk为p为量测集合的Zk的一个划分子集;ωp为划分p的权值;|W|为子集W内元素的个数;dW为观测子集W的非负系数;φZ(x)为扩展目标量测的似然函数;λk为单位空间内的杂波个数;ck(Zk)为杂波的分布函数[10]。
1.2 ET-GM-PHD滤波算法
2006年,VO等人在文献[11]中给出了PHD滤波的高斯混合实现形式,在此基础上,2010年,Granstrom等人提出了ET-GM-PHD滤波。ET-GM-PHD滤波算法和标准的GM-PHD滤波算法的预测步和更新步一致,本文只给出了标准GM-PHD滤波算法的预测和更新方程。
GM-PHD滤波器满足以下假设条件:
(1) 每个目标的运动模型和量测模型均为高斯线性的;
(2) 目标的生存概率和检测概率与目标状态相互独立;
(3) 新生目标的RFS强度为高斯混合形式。
基于以上假设,GM-PHD滤波器的预测步可表示为
(4)
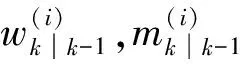
更新步可表示为
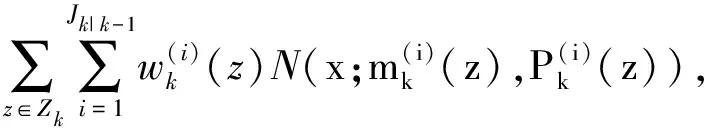
(5)
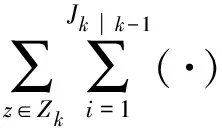
1.3 量测划分问题描述
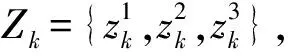
可见,随着量测点的增加,划分数目将急剧增加,计算量将大幅增大,影响跟踪的实时性,因此寻找准确快速的量测划分算法,是ET-GM-PHD滤波中的重要环节。针对这个问题,本文提出了一种基于LOF检测的SNN相似度的量测划分算法。
2 基于LOF检测的SNN相似度的聚类算法
本文针对不同扩展目标产生量测密度差异较大的情况,结合局部异常因子离群检测技术和SNN相似度,提出了一种改进的ET-GM-PHD滤波算法,减小了算法的运行时间,提高跟踪的稳定性。
2.1 基于LOF的量测集预处理
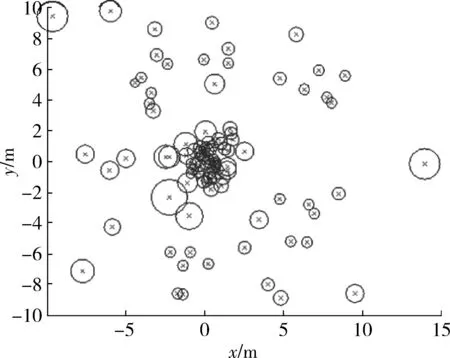
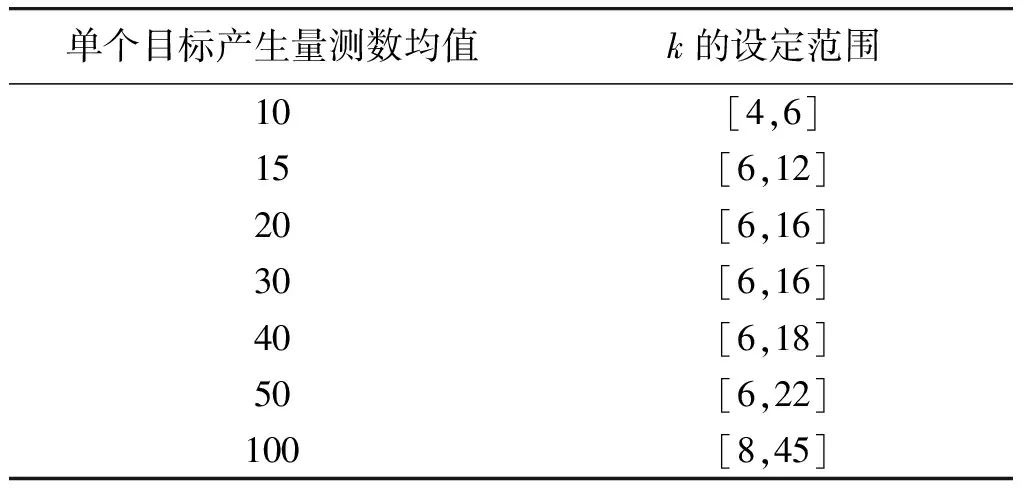
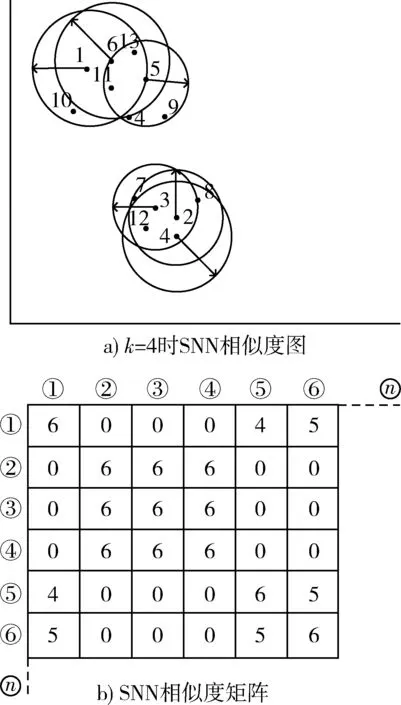
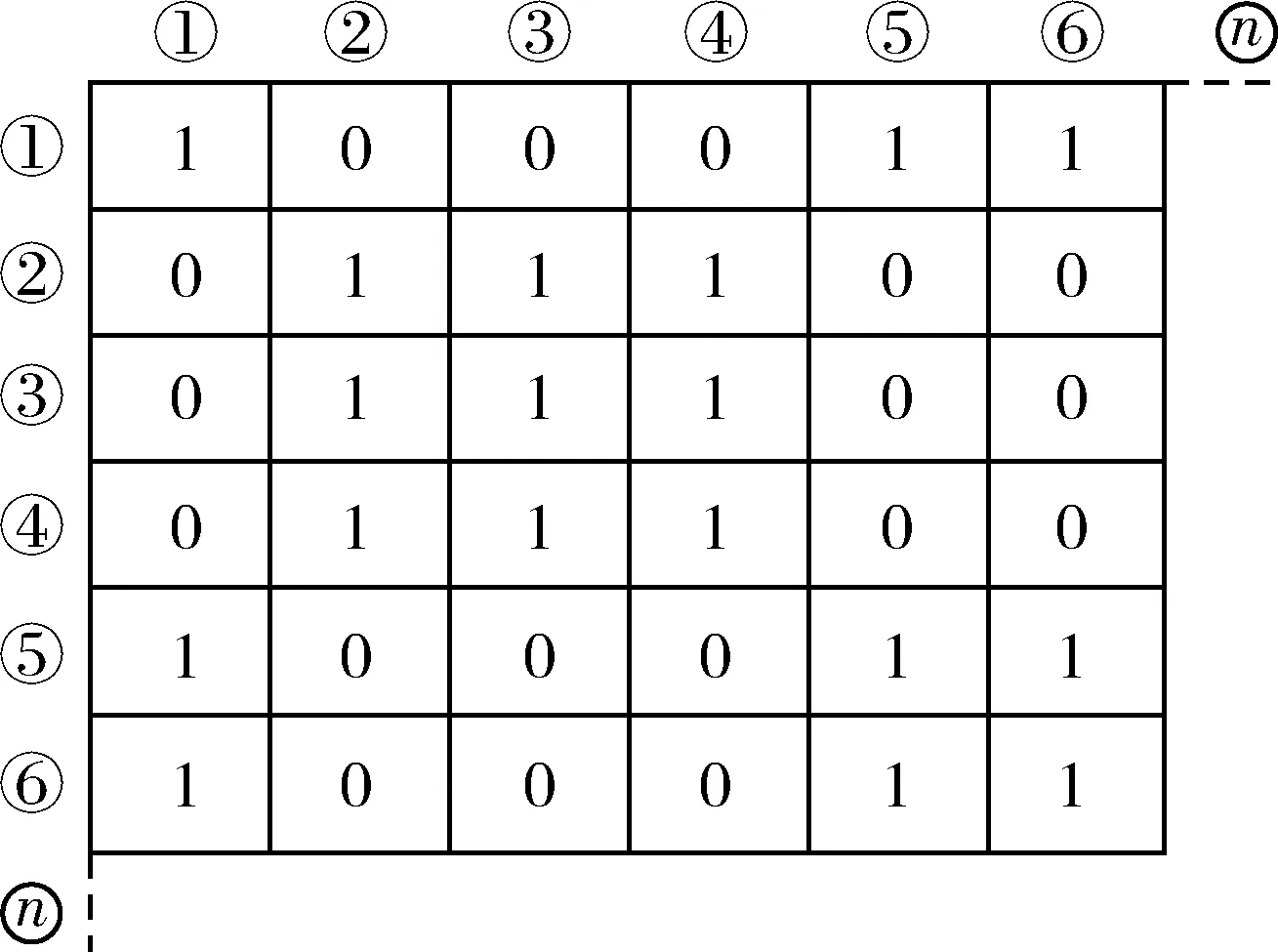
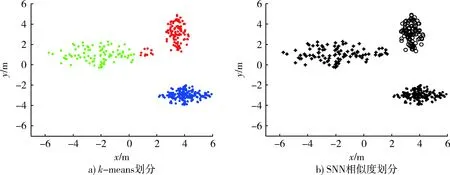
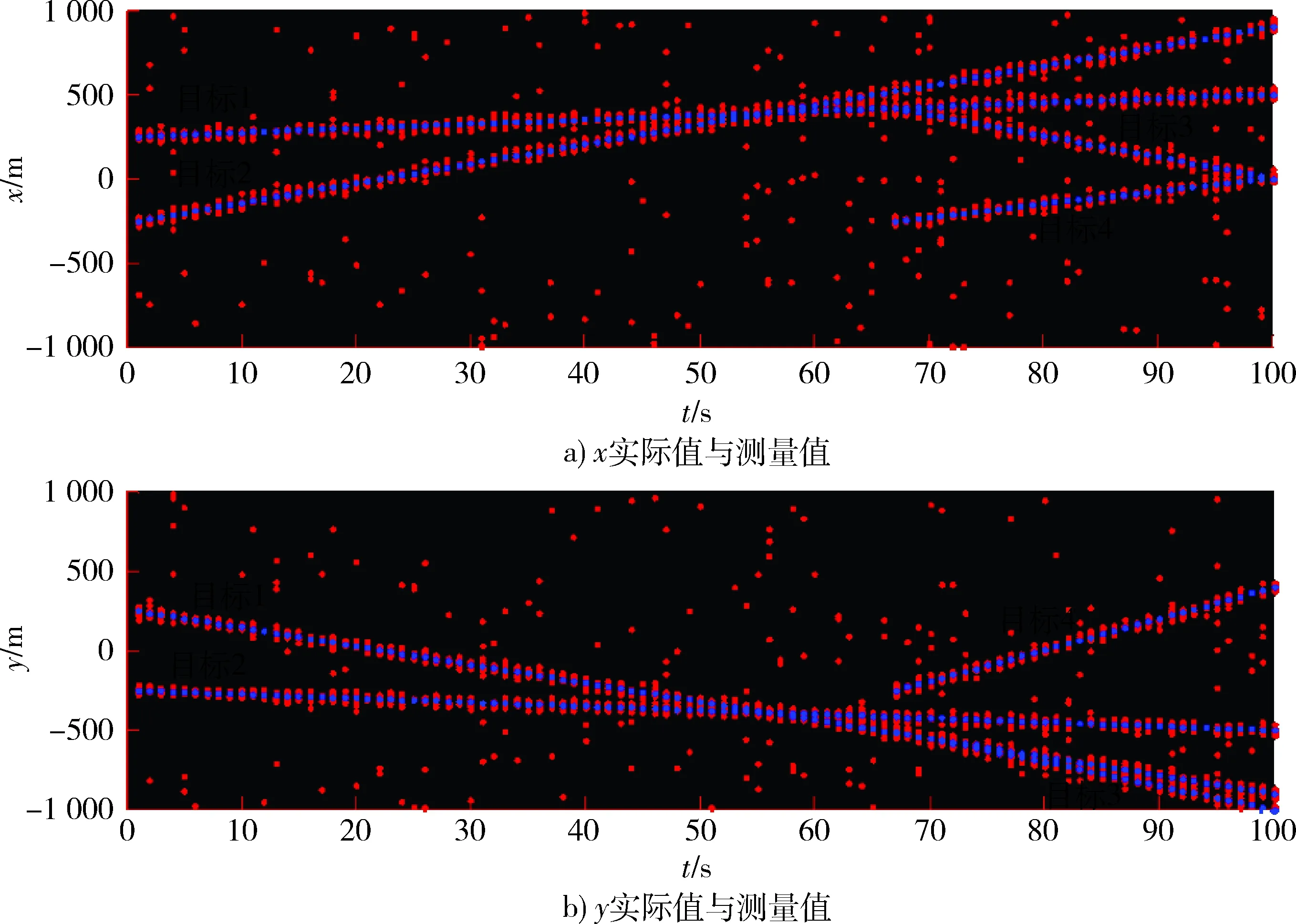
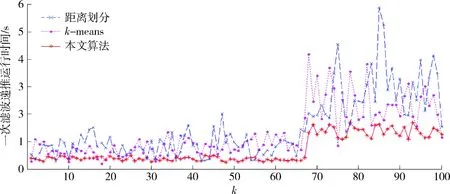
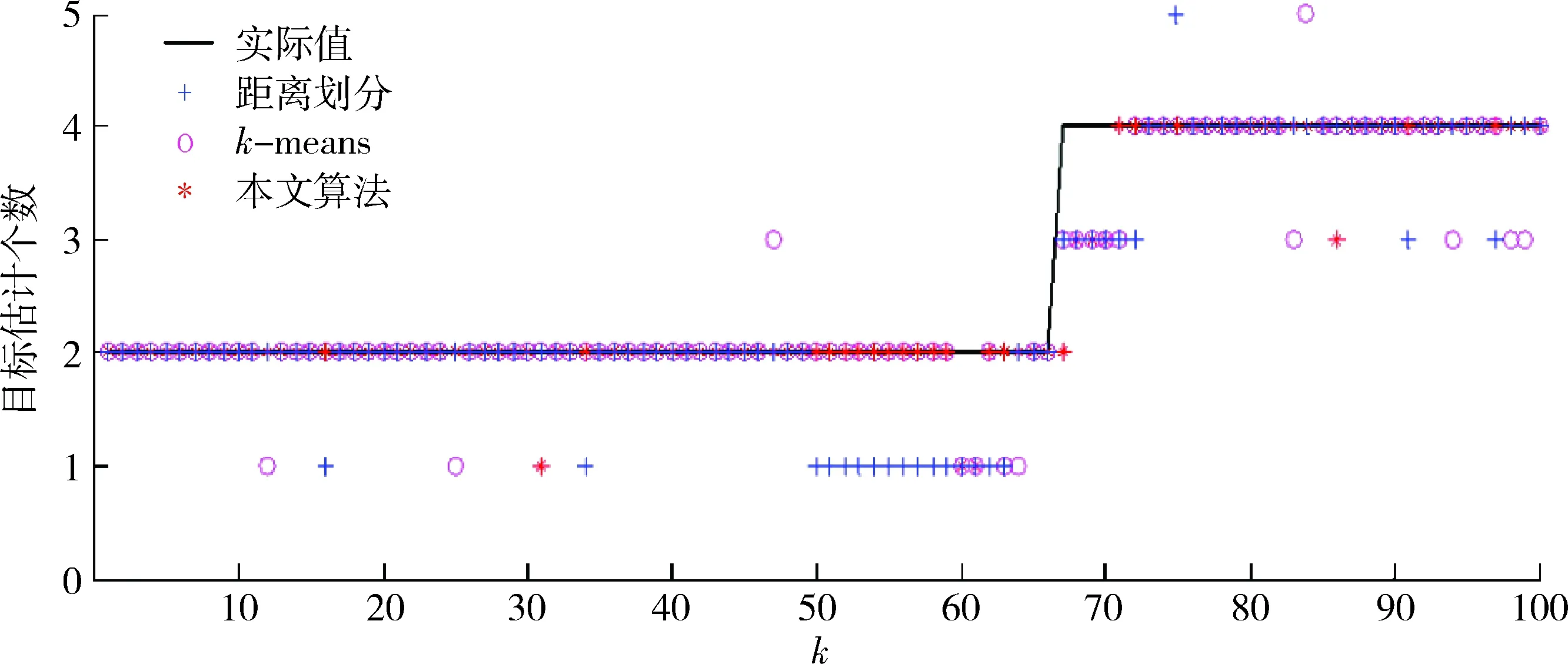
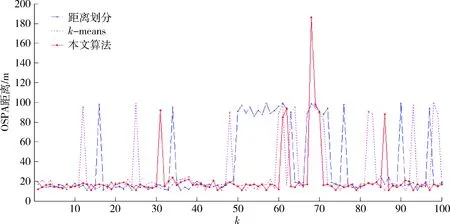
定义1第k距离dk(p):对于点p的第k距离dk(p)有如下定义:dk(p)=d(p,o),d(p,o)表示p,o2点之间的欧式距离,即直线距离,并且dk(p)满足以下要求:①在集合中至少有不包含p点在内的k个点o,∈C{x≠p},满足d(p,o,)≤d(p,o);②在集合中最多有不包括p在内的k-1个点o,∈C{x≠p},满足d(p,o,) 图1 点p的第5距离Fig.1 The fifth distance of point p 定义2第k距离邻域Nk(p):p的第k距离以内的所有点,包括第k距离点。 定义3可达距离reach-distk(p,o):点o到点p的可达距离定义为reach-distk(p,o)=max{dk(o),d(p,o)},如图2所示,o1到p点的第5可达距离为d(p,o1),o2到p点的第5可达距离为d5(o2)。 图2 可达距离示意图Fig.2 Reachable distance schematic diagram 定义4局部可达密度lrdk(p):表示点p的第k邻域内的点到p点的平均可达距离的倒数,定义为 (6) 定义5局部异常因子LOFk(p):表示点p的邻域Nk(p)的局部可达密度与点p的局部可达密度之比的平均数,定义为 (7) 这个比值越接近于1,说明p和其邻域点的密度越接近,p可能和邻域属于同一簇;如果这个比值小于1,说明p点的密度大于其邻域点,p为密集点;如果比值大于1,则p点密度小于其邻域,p点倾向于异常点[12]。 图3是LOF的实例图,量测点周围的圆的半径与局部异常因子成正比,圆的半径越大,量测点越偏向于异常值[13]。通过选取合适的LOF阈值,对量测集进行杂波滤除,将局部异常因子大于阈值的量测点视为杂波滤除。LOF阈值可以通过以下方法来选择:将局部异常因子从大到小排列,并绘制曲线,选取斜率最大部位的点作为LOF阈值即可。经过LOF异常值检测过滤后,杂波大量被剔除,算法计算复杂度降低25%~35%。 图3 LOF实例图Fig.3 LOF instance diagram 定义1(共享最近邻相似度):共享最近邻相似度的基本思想是:当2个量测点包含一定数量的最邻近点时,则认为这2个量测点相似。本文中引用文献[14-15]的相关概念对SNN相似度进行定义:假设量测集X={x1,x2,x3,…,xN},xi,xj∈X,定义xi的k-邻域为 (8) 式中:Vk(xj)为xj的k-邻域。 如果xi∈Vk(xj)且xj∈Vk(xi),则xi和xj的共享最近邻SNN(i,j)=|Vk(xi)∩Vk(xj)|,|·|表示集合中元素的个数;否则SNN(i,j)=0。 SNN相似度计算的伪代码如下 初始化k; 令Xun=X; 计算数据集X的距离矩阵; IfXun≠∅,则 {任意选择一个x∈Xun; 计算x的k-领域Vk(x)={x1,x2,…,xk}, 其中x1,x2,…,xk是x的k-领域中的数据点 Fori=1,i≤k {ifx∈Vk(xi)则 SNN(x,xi)=Vk(x)∩Vk(xi); else SNN(x,xi)=∅;} Xun=Xun-Vk(x);} End If 算法中的k值需要人为设定,k值的大小与单个目标产生量测点的个数有关,量测值数目的多少由传感器精度和扩展目标距离传感器的距离决定。当传感器精度较差或者扩展目标距传感器距离较远的情况下,单个扩展目标产生的量测点可能少于20个;反之,若传感器精度较好或者扩展目标距传感器较近时,单个目标可能会产生大于20个量测值。在控制其他变量的情况下,改变单个目标产生的量测点个数,对划分结果进行分析,统计k值的合适取值。本文借鉴文献[8]的统计结果,结论中覆盖范围较广,本文假设单个目标产生的量测值个数均值分别为10个、20个和30个,在表1的统计结论范围之内。 表1 参数k的设定范围Table 1 Setting range of parameter k SNN聚类是将SNN相似度大于一定阈值sl的量测划分到同一簇中,具体的实现步骤如下: 步骤1:计算经过LOF检测滤波后的量测两两之间的欧式绝对距离,找到每个点的k个最近邻点。 步骤2:计算每2个量测值之间的SNN相似度,并建立n维SNN相似度矩阵S,n是量测点的个数,矩阵S建立的示意图如图4所示。 图4 建立SNN相似度矩阵Fig.4 Establishing SNN similarity matrix 步骤3:从{0,k-1}之间选取合适的相似度阈值sl,不同的sl得到不同的划分结果,经过多次的实验结果分析统计,本文选取sl=k/2。 步骤4:对于相似度矩阵S中≥sl的相似度用1 表示,其余用0表示,得到矩阵Sth,图5是图4b)在sl取3时得到的矩阵,将矩阵Sth中同一个的1连通域对应的量测置于同一个簇,连通域的个数即为簇的个数。 图5 SNN相似度矩阵SthFig.5 SNN similarity matrix Sth 如图6所示,分别是采用k-means划分算法和本文算法对量测密度差异较大的3个量测集产生的划分结果,图6a)中2个目标量测集划分出现了混淆,这是因为目标两目标量测密度差异较大,且距离相近;图6b)是本文算法得到的划分结果,可以看到,量测集得到了正确的划分。 在本次仿真实验中,采用ET-GM-PHD滤波器,进行100次蒙特卡罗仿真,共设置4个量测密度相差较大的跟踪目标,其中目标1,2的量测密度服从λ=10的Poisson分布,目标3,4的量测密度分别服从λ=20和λ=30的Poisson分布,使用基于距离划分的算法和基于k-means划分的算法和本文提出的算法进行比较,验证本文算法的可行性。 图6 k-means划分和SNN相似度划分效果图Fig.6 k-partition and SNN similarity partition effect diagram 本次实验对[1 000,1 000] m×[1 000,1 000] m的二维空间区域进行观测,如图8所示,扩展目标的运动区域限定在x轴的-1 000 m至1 000 m,y轴的-1 000 m至1 000 m。扩展目标的运动状态和始末时间如表2所示。 表2 目标初始状态和始末时间Table 2 Target initial state and start-end time (9) (2 m/s)2I2的高斯白噪声,I2是二维单位矩阵。 量测方程为 (10) 式中:量测噪声vk是均值为0,协方差为Rk=(20 m/s)2I2的高斯白噪声,各目标产生的量测相互独立。 新生目标强度为 衍生目标强度为 γβ(x)=0.05N(x;ξ,Pβ), 式中:ξ为本体状态,Pβ=diag(100,100,400,400)。 高斯混合相关修剪与合并参数:最大高斯分量数J=100,修剪门限T=1e-5,合并门限U=5,势误差与状态误差的调节因子c=10,OSPA取二阶距离p=2。 图7给出了目标和杂波的态势图,目标1,2起始于1 s,消亡于100 s;目标3,4起始于66 s,消亡于100 s,杂波的个数服从λ=10的Poisson分布。 图8给出了3种算法进行一次滤波递推的运行时间,从图8中可以看出,基于距离划分和基于k-means划分的ET-GM-PHD滤波耗时明显高于本文提出的算法。这是因为本文算法在进行量测划分阶段前进行了LOF检测杂波滤除,并且基于SNN相似度的划分算法在划分量测密度差异较大的量测集时具有优势。 图7 目标和杂波的态势图Fig.7 Situation map of target and clutter 图9是3种算法对目标个数估计的方针图,从图9中可以看到,在k=16,34,50~63,67~72,75,90,96 s时刻,基于距离划分的ET-GM-PHD滤波算法对目标个数的估计与真实值出现了误差;k=11,25,47,60,61,63,64,67~71,82,83,92,98,99 s时刻,基于k-means划分的算法对目标个数出现错误估计;本文算法只在k=31,60,61,67~71,86 s时刻出现了目标个数的误估。这是由于本次实验仿真中的目标产生量测密度差异较大,当目标接近时,传统的基于欧式距离的划分方法会出现量测集的错分,因而出现目标个数估计的偏差,而本文的算法是基于SNN相似度,考虑的是量测值周围的信息,因此划分效果比较理想,提高了滤波器跟踪的稳定性。 最优子模式指派(optimalsubpatternassignment,OSPA)距离是一种评价随机有限集框架下多目标跟踪性能的指标[16],它是度量2个集合间差异度的误差距离,其表达式为 (11) 图10给出了3种算法的OSPA距离,可以看到,代表基于距离划分算法的蓝色虚线和代表k-means划分算法的紫色点画线波动次数较多,并且波动时间较长,而代表本文算法的红色实线仅有4处波动,且波动时间持续较短,说明本文算法的跟踪稳定性更好。 从上述仿真结果中可见,本文提出的算法相较于传统的基于距离和k-means划分的算法具有明显的优势,算法的运行时间和跟踪的稳定性都有一个较好的优化。 图8 一次滤波递推耗时对比Fig.8 Comparison of once filter recurrence time consuming 图9 目标估计个数对比Fig.9 Comparison of the number of target estimates 图10 OSPA距离对比Fig.10 OSPA distance contrast 在扩展目标产生的量测密度差异较大的情况下,传统基于距离划分的ET-GM-PHD滤波算法跟踪效果不佳。针对这个问题,本文提出了一种基于LOF检测的SNN相似度的ET-GM-PHD滤波算法,并进行了仿真对比实验。实验结果表明,本算法在减少计算时间的同时,跟踪性能的稳定性也得到了保证,对比于传统方法具有较大优势。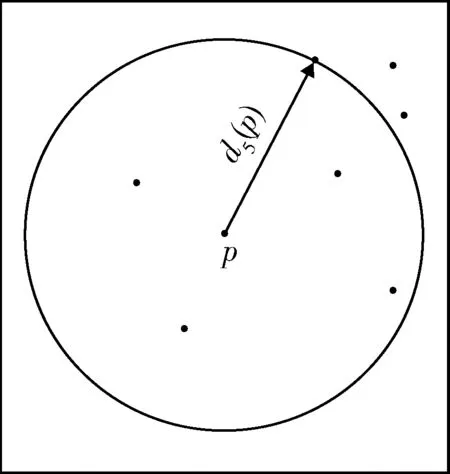
2.2 基于SNN相似度的聚类算法
2.3 SNN聚类仿真实验
3 仿真实验与分析
3.1 仿真场景设置

3.2 仿真结果分析
4 结束语
