复杂地形条件下近炸引信回波信号分析*
2019-03-12岛新煜高敏李超旺
岛新煜,高敏,李超旺
(陆军工程大学石家庄校区,河北 石家庄 050003)
0 引言
毫米波由于容易实现较大频偏,在近程探测时的衰减小等固有优势而在近炸引信的应用中愈发受到关注[1]。为实现高精度的近炸探测,首先需要对回波信号进行正确的分析。引信接收机中接收到的回波信号除了含有距离信息的信号外,还有各种噪声干扰以及地面杂波信号。特别是在近炸引信的工作过程中,由于回波延迟短,作用距离近使得地面杂波的影响尤为突出。大量的杂波信号使距离信息淹没其中,而不同地形条件下的地杂波对回波信号的影响又各不相同,只有掌握杂波功率谱的分布状况才能更好地对杂波进行抑制,同时准确地分析回波信号的特征又是提取有效距离信息的关键,为此建立更加符合地表变化的杂波模型对回波信号的处理及提高测距精度具有十分重要的意义。
当前,研究者们为分析雷达信号,主要采取建模和实地测量的方法。针对不同工作体制下雷达回波信号的仿真和模拟提出了许多的建模方法[2-5]。针对不同的工作环境提出了一些杂波模型,较为经典的有瑞丽分布,对数-正态分布、韦伯尔分布、K分布[6-10]等。然而这些基于随机统计过程提出的分布模型在实际的应用中本身就会受到使用条件的限制,同时,在某些地形条件下,并不能完全反映地形变化对回波信号的影响。而采用实地测量的方法分析回波信号则需要花费大量的人力物力,此外在复杂山地或地势险峻的条件下无疑会给测量带来诸多不便。为此,本文利用数字高程模型作为数据库,针对选取的分析区域进行杂波仿真。通过高程信息和提取的相关地形因子对分析区域进行划分,并提出不同区域采用不同的杂波计算方法,分析了回波信号在噪声及所建杂波影响下的特征,为回波信号的处理奠定了基础。
1 回波信号分析
引信回波信号的组成如图1所示。对于无线电引信,其工作体制通常采用三角波线性调频体制(frequency modulation continue wave,FMCW),利用发射信号和接收到的回波信号的频率差值,即差拍信号的大小来计算引信与地面或目标间的距离。实际情况中,弹目之间的相对运动会产生多普勒频移继而对差频频率造成影响,其发射信号、接收信号与相应差拍信号的时频关系如图2所示(图中fi指差拍频率)。在上扫频段,多普勒频移会使差拍频率降低;而在下扫频段,多普勒频移的影响会使差拍频率增大[11]。
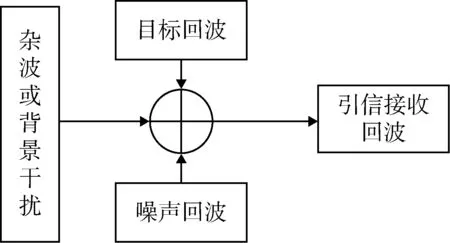
图1 引信回波信号的组成Fig.1 Constitution of fuze echo signal
在一个扫频周期内,上扫频段的发射信号可以表示为
(1)
式中:A0和φ0分别为发射信号的振幅和初始相位;f0为载波频率;μ为调频斜率,μ=4ΔFm/T,其中,ΔFm是发射信号的最大频偏,T指一个调制周期。

图2 FMCW的时频关系图Fig.2 Time-frequency relation of FMCW
下扫频段的发射信号可以表示为
(2)
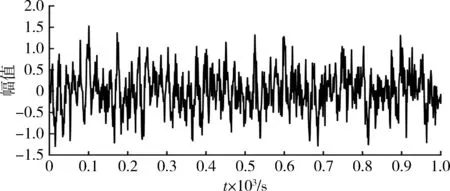
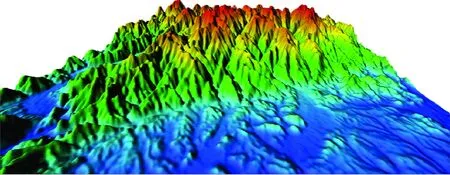
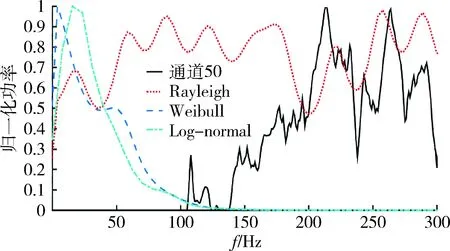
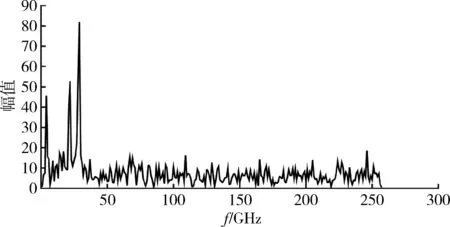
由于在三角波调频时,差频信号的频率与传播时间的关系在0 Sr(t)=A0Krcos[2π(f0(t-τ)+ (3) 式中:Kr为常量,与信号传播的衰减及反射强度有关;φ0代表反射信号产生的附加相位;τ为回波延迟,τ=2(R0-vt)/c=τ0-kt,其中,R0表示初始时刻的弹目距离,v表示弹目的相对速度。 将(1)与(3)进行混频,得到差拍信号的表达式为 (4) 从式(4)可以看出,经过差拍运算后的信号依旧是一个线性调频信号。 引信接收机中的噪声除了从外界接收到的噪声,还有接收机自身产生的噪声。对于毫米波段的雷达系统,接收机本身产生的内部噪声是影响回波信号的重要因素。经过充分的理论分析和测试研究,接收机的内部噪声以高放部分的噪声形式存在,因此,在进行噪声模型的仿真过程中,通常将回波信号中的噪声视为高斯白噪声。 (5) 噪声的功率为 Pn=N0Bn, (6) 式中:N0为接收机输出端噪声的功率谱密度,N0=k0T0Fn,k0为玻尔兹曼常数,T0为标准温度,Fn为接收机的噪声系数;Bn为接收机噪声的带宽,通常取3 dB作为参考值。 近炸引信的工作特点决定了其回波信号会受到较强的地杂波的影响。与传统基于随机统计的方法建立的地杂波模型不同,本文结合数字高程地图,首先对所选区域的高程信息进行处理,通过高程值提取坡度、地形起伏度、地面粗糙度和高程变异系数等地形因子作为划分依据,针对不同的区域选择合适的后向散射系数及相应后向散射截面的计算方法,继而建立反映复杂地形条件下的地杂波模型。 数字高程模型是用一组有序数值阵列形式表示地面高程的一种实体地面模型。在实际运用中,可以直接根据经纬度信息从地理空间数据云中获取相应区域的数字高程地图,该地图以高程数据存储,且各数据点间的网格间距相等。但是,从地理空间数据云中下载的高程模型并不能直接进行计算,需要借助Global Mapper软件事先对高程数据进行格式的转换,将高程模型转换成三维坐标的存储格式,即x坐标代表经度,y坐标代表纬度,z坐标代表高程值,通过高程值再计算坡面因子。坡面因子主要分为微观坡面因子(如坡度、坡向、平面曲率、坡长等)和宏观坡面因子(如地表粗糙度、地形起伏度,高程变异系数等)。其中,影响地貌类型划分的显著地形因子主要有坡度、地形起伏度、地表粗糙度和高程变异系数等。考虑到在后续散射截面的计算中主要根据地貌类型对区域进行分割,因此,根据数字高程数据分别计算所选区域的坡度、地形起伏度、地表粗糙度以及高程变异系数[12]。 3.1.1 坡度的计算 坡度反映了局部地表坡面的倾斜程度,其大小可以由两点之间的高程差与水平距离的比值求得。由于数字高程数据是一系列的关于地面坐标离散的点,可以用Z(x,y)表示地面高程的曲面函数,Z表示该点的高程值,x和y分别代表该点的经度和纬度,则坡度的计算公式为 (7) 式中:∂Z/∂x和∂Z/∂y分别表示高程沿经度和纬度方向上的变化率。 3.1.2 地形起伏度的计算 地形起伏度是指在所指定的分析区域内所有栅格中最大高程与最小高程的差。计算公式为 RF=Hmax-Hmin|Hmax,Hmin∈Ai, (8) 式中:Hmax和Hmin分别表示分析区域内高程的最大值和最小值;Ai表示分析区域。在此,为了便于计算,取3×3的分析窗口作为单位分析区域对所选取的地形进行计算。 3.1.3 地表粗糙度的计算 地表粗糙度能够反映地表的起伏变化和侵蚀程度,一般定义为地表单元的曲面面积与其在水平面上的投影面积之比。在已经提取坡度的前提条件下,有一种简便的计算方法,记地表粗糙度为Rf,则 Rf=1/cosS, (9) 式中:S为坡度。 3.1.4 高程变异系数的计算 高程变异是反映分析区域内地表单元格各顶点高程变化的指标,用分析单元各点的标准差与其平均高程的比值来表示,即 (10) 根据计算的地形因子,以高程值为主导,坡度和地形起伏为显著因子,地表粗糙度和高程变异系数为辅助因子,按照文献[13]中的划分标准对选择的分析区域进行定量划分,将陆地地形划分为平原、丘陵,高原及山地,具体划分依据见表1。通过表1发现,各种地形因子在不同地形间有重叠的部分,这是因为真实的场景中很少存在单一地形。因此在实际应用中,划分过程采取三级划分指标,即高程值作为确定地形的一级指标,坡度和地形起伏作为二级指标,地表粗糙度和高程变异系数作为三级指标。划分时,首先用高程值预判当前区域是否属于某一确定地形,若不是则继续采用二级指标进行确定;利用计算的坡度和地形起伏对不能确定地形类别的区域进行判断,如仍不能确定地形则继续利用地表粗糙度和高程变异系数进行最终确定。 表1 不同地形的划分依据Table 1 Basis of different landform division 通常情况下,综合考虑高程值和4种地形因子能够对地形有一个较好的划分,根据划分的地形再计算相应的杂波散射单元面积。 传统杂波散射单元面积的计算通常是基于网格映像法,即根据距离环或距离-多普勒环对照射区域进行统一的划分[14]。这种方法在地形起伏不大的地区具有很好的效果,然而当分析区域存在较大的起伏时,再利用这种方法计算杂波散射单元的面积便会产生较大误差。因此,在进行杂波散射单元面积的计算时针对不同的地形应当采取不同的计算方法,其描述如下: (1) 对于平原。地形起伏度和地表粗糙度往往比较小,可以将其认为是一个平面,经由地面反射的回波视为镜面反射,所以直接根据雷达照射区域的等效几何面积计算杂波的散射面积。 (2) 对于丘陵。地形具有一定的起伏,此时,采取规则的矩形网格划分,统计分辨单元内数据点的个数,将分辨单元内的所有数据点视为一个新的散射单元,则杂波的散射单元面积就等于分辨单元内各点散射体面积的叠加。 (3) 对于山地和高原。地形的起伏通常较大,此时,若再采取矩形网格划分,则不能很好地表征山地地形起伏的特点。因此,考虑到数字高程数据的特点,在规则矩形网格划分的基础上,将数字高程数据中每相邻3个点作为一个单位面元,认为每一个单位面元都是一个小平面,即用单位平面模型来代替杂波的散射单元面积。 根据雷达方程,接收机接收到的由地面返回的杂波功率表示为 (11) 式中:Pt指发射信号的功率;G0指系统增益;σ是杂波的散射截面积,一般由后向散射系数和散射面积的乘积计算得到,即 σ=σ0Aσ, (12) 式中:σ0为杂波单元的后向散射系数;Aσ为杂波散射单元的面积。考虑到毫米波引信的工作频段,后向散射系数采用修正的Morchin模型,即 (13) 首先对噪声环境下的FMCW回波信号进行仿真,仿真的主要参数为:起始载波频率为24 GHz,调制周期为10 μs,最大频偏为2 GHz,弹目起始距离为20 m,引信相对地面的速度为400 m/s,波长为5 mm,在Matlab中实现含噪信号的混频运算,得到差拍结果(在此只截取了部分周期内的信号)如图3所示。 图3 含噪的差拍信号Fig.3 Beat signal with add-noise 从地理空间数据云中30 m分辨率的地理数字地形模型中选取福建省某一复杂山地地形(北纬28.7°~28.9°,东经118.9°~119.1°)进行相应的杂波仿真,选取的地形如图4所示。为便于观察和分析,在仿真时,将山地的位置进行适当调整,得到地杂波的功率谱如图5所示。 图4 选取的原始地形图Fig.4 Map of original selected terrain 为进一步说明本文得到的杂波功率的特点,选取不同距离通道内(在此分别选取距离通道为50,100,200,300)的杂波功率谱并作归一化处理,与常用的反映地面杂波分布的模型,即Rayleigh分布、Weibull分布和Log-normal分布的归一化功率谱作对比,比较结果如图6~9所示。 图6 距离通道为50的功率谱对比Fig.6 Comparison of power spectrum with range 50 图7 距离通道为100的功率谱对比Fig.7 Comparison of power spectrum with range 100 图8 距离通道为200的功率谱对比Fig.8 Comparison of power spectrum with range 200 图9 距离通道为300的功率谱对比Fig.9 Comparison of power spectrum with range 300 由图6~9的结果可以明显看出,在复杂山地条件下的杂波回波较与传统的杂波模型有较大的偏移,并不能用某一特定的模型表征。这是因为,传统的杂波模型并没有考虑具体的地形环境及雷达的工作特点,具有很强的局限性,在地形起伏大的地区,如果单纯将雷达的照射区域视为一个平面,势必会造成较大的误差。此外,可以发现,杂波的功率变化没有明显的规律性,且经常会有较大的抖动和突变,这是由于山地的陡峭变化使得回波信号在各物体间发生的多次折射现象对结果造成了影响。杂波功率的变化性和起伏性较大,充分体现了杂波在复杂地形下的非均匀性。 在前述分析和仿真的基础上,将地杂波的影响、噪声的干扰以及不含噪声的回波进行相干叠加,得到引信接收机中最终接受到的回波信号,其幅频特性曲线如图10所示。图10的结果表明,在近炸引信的工作过程中,回波信号中受到了地杂波和噪声的干扰导致频谱中出现了多个峰值。由于弹目间的距离比较近,发射信号经地面反射后有大量的杂波直接被引信的接收机所接受。这些杂波会对距离信息造成干扰,有的甚至会淹没距离信息。这就要求在后续的信号处理过程中,在考虑近炸引信信号处理时间短的特点的同时对杂波进行有效的抑制,并且还应考虑对于距离信息的准确提取以便满足高精度测距的要求。 图10 相干叠加后的回波信号Fig.10 Echo signal after coherent addition 结合毫米波近炸引信的工作特点,本文利用数字高程地图,提出了一种符合地形起伏特点的回波信号模拟方法,按照这种方法模拟的回波信号能够反映地形对回波信号的影响。同时,对最终叠加的信号进行分析,指出地杂波在近炸引信工作时的影响特点,为今后的杂波抑制和距离信息的提取等信号处理提供了参考。
2 噪声模型
3 杂波建模
3.1 地形因子的提取
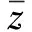
3.2 杂波散射单元面积的计算

3.3 杂波功率计算

4 仿真校验及分析
4.1 噪声环境下的回波信号
4.2 复杂山地下的杂波回波信号



4.3 噪声、地杂波叠加后的回波信号
5 结束语
