防空武器系统复杂地形部署标定方法研究*

谢瑞煜，孙瑾，赵建军

(海军航空大学，山东 烟台 264001)

0 引言

现代局部战争是一场在高技术条件下的战争，空中目标威胁呈多样化发展,且威胁程度日趋增大。海湾战争以来的历次战争表明：空袭与反空袭已成为主要的作战样式，并贯穿于战争的始终且影响着最后的胜负。随着科技水平的不断进步，无论在海上还是在陆地，空中目标特别是导弹的威胁变得越加复杂多样，高速度、隐身化、复杂电磁环境，都给反空袭带来了巨大的考验。因此，拥有完善的防空武器系统是能否有效反空袭的关键[1]。

防空武器系统按距离分为远程、中程、近程防御。其中近程防御是最后一环也是很关键的一环，它可以对来袭的导弹、固定翼飞机、直升机等目标进行精确打击，确保在中远程的防空网打击下的漏网目标得到彻底的摧毁，避免己方目标的损失。

随着美军亚太再平衡战略的提出和付诸实施，海空军对领海、领空的抵近侦察次数快速增长，沿海防空压力日趋渐大，除了海基防空力量的亟待增强，陆基防空武器系统重要性也与日俱增[2]。

近防武器系统在部署时需要一定隐蔽性，在这种背景下，考虑到沿海环境的具体情况，大量近防武器系统需要部署在复杂环境中。众所周知，沿海地区地形复杂，特别是在沿海地形一般多山，林木茂密。近防武器系统在展开部署时，虽然隐蔽性可以大大增加，但因此会受到不少影响[3-4]。防空武器系统在阵地部署时，必须先进行标定，按照战术技术的要求，防空武器系统在作战状态时，必须纳入防空情报网，武器系统应具备定向定位的手段。它是通过地面作战系统中的指挥单元来实现的。同时由于地面作战系统的各设备在阵地上是分散布置的，为完成各车间的目标坐标的传输、变换和修正等，作战装备间应进行方位和距离的标定，即确定各车之间的相对距离和相对方位角度[5]。

比如某型防空武器系统的标定包括指挥单元(A)的绝对标定及指挥单元、火力控制单元(B)和武器单元(C)之间的相对标定。

1 标定方法

1.1 标定方法介绍

标定过程中需要进行A载体绝对标定以及A与B与C载体的相对标定[6-7]。

绝对标定一般采用数字罗盘或者陀螺寻北仪进行标定。数字罗盘的原理是测量地球磁场，如果在使用的环境中有除了地球以外的磁场且这些磁场无法有效屏蔽时，那么数字罗盘使用就有很大的问题；与此相反的是，陀螺寻北仪是一款有高精度双轴动力调谐陀螺，它是通过测量地球自转角速度，自主确定所附载体的真北方向值，不受外界磁场或其他环境的干扰和影响。基于沿海环境的特点，选取陀螺寻北仪进行绝对标定比较合适。

各车之间的相对标定即相对距离和相对方位角度的确定有多种方法，主流的有如下几种：

(1) 采用经纬仪进行相对标定的方法

该方法利用经纬仪对各载体进行相对方位的确定；而且经纬仪也具有一定的测距功能，能将相对距离标定出来。经纬仪定位时在远距离(1 km以上)精度大大下降，不适合进行测距，测量时间在10 min以上[8]。

(2) 采用瞄准望远镜加激光测距仪的光学互瞄法进行相对标定的方法

该方法是传统的标定方法；在进行绝对标定后，通过用瞄准望远镜互瞄A载体和B载体雷达上的十字标识，对两载体的相对方向进行标定，最后利用激光测距仪对各车进行测距。该过程在模拟中，时间在3～5 min，定位定向时，两者距离在远距离(1 km以上)，精度在分米级水平，方位角误差小于1°[9-11]。

(3) 采用差分GPS进行相对标定的方法

差分是指1个观测点对2个目标的观测量、2个观测点对1个目标的观测量或1个观测点对1个目标的2次观测量之间求差，作用是消除观测方程中的公共项，以提高定位精度。差分GPS通过消除观测方程中的公共项，理论上可以消除卫星部分的全部误差和信号传播部分的部分误差。在进行热启动下，采用平滑伪距的DGPS能达到厘米级的精度，算得距离误差不超过10 cm，方位角误差不超过0.1°；首次定位时间一般在30 s左右；最后总标定时间不超过1 min[12-14]。

1.2 标定方法对比

根据一般沿海环境特点，对上述方法进行简单分析，可得到以下结论，如表1所示。

按传统方法(光学互瞄法)作为基准定位时间和精度，采用差分GPS在时间上快2 min以上，在定位定向精度上最优可以缩小一个数量级。因此采用差分GPS进行标定具有最大的优势，是未来防空武器系统标定方法的趋势。

表1 不同标定方法对比Table 1 Comparison of different calibration methods

2 标定方案

将A载体上的陀螺寻北仪打开，测得A载体雷达机械零位与正北之间的夹角，从而对整个系统进行正北绝对标定。与此同时，打开车载GPS定位设备，测得A，B，C载体等定位数据，并将其通过无线数传设备运往差分基准站，与基准站GPS天线获取的实时数据进行差分处理，消除单设备接收卫星信号时造成的误差，得到A，B，C载体等定位真值。将获取的定位真值通过车载数据处理系统，求出A与B载体和B与C载体的相对方位角和相对距离。最后将绝对标定和相对标定值装进行装订，完成近防武器系统的阵地标定。

标定示意图如图1所示。

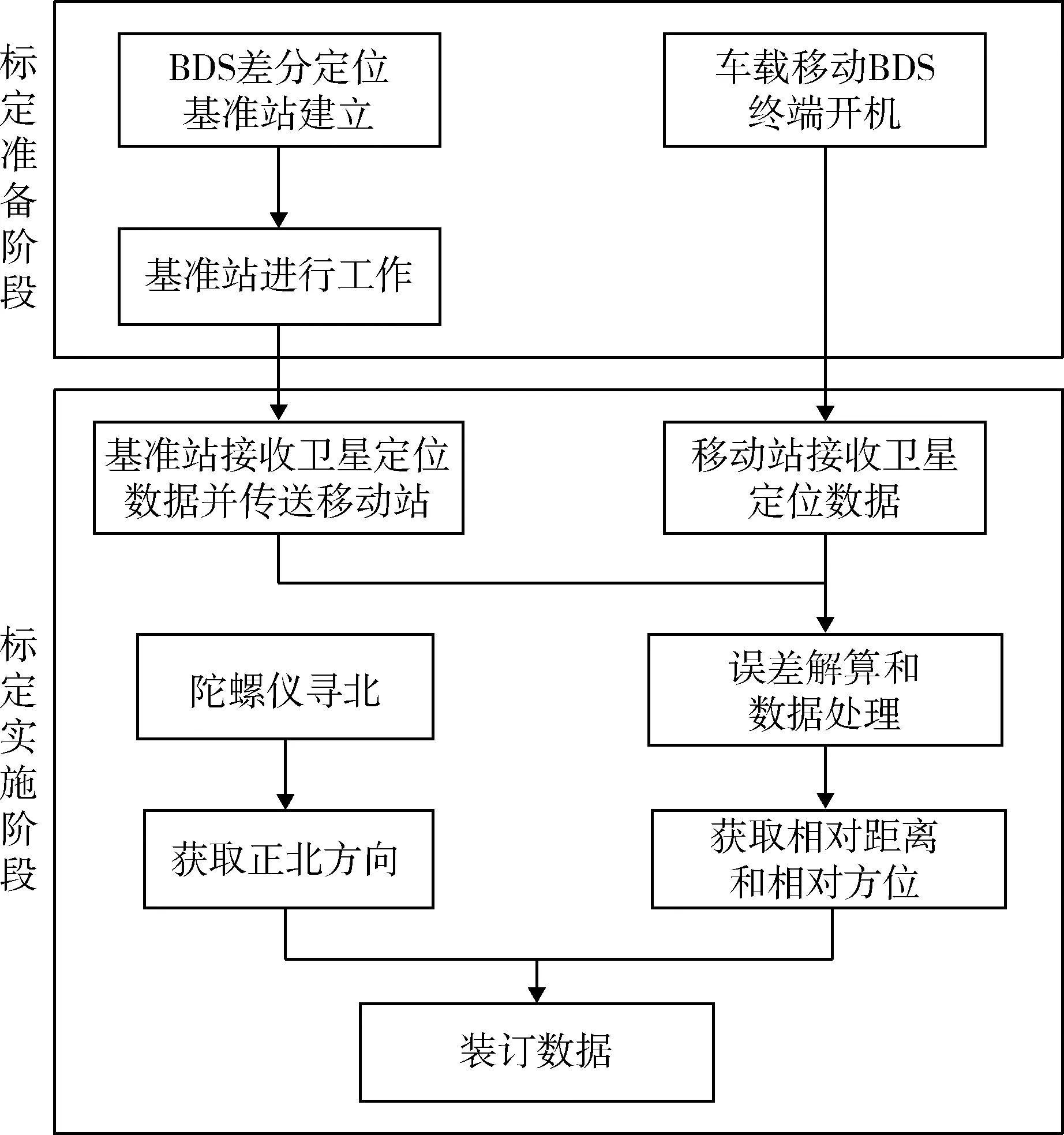
图1 基于差分GPS的标定示意图Fig.1 Calibration schematic map based on differential GPS

3 数据处理

两点距离及方位角计算中，采用航空航天领域里的传统方法已经很成熟，很难做到理论性的创新。在一般的短距离测量情况下，本文通过引进测绘领域的方法，忽略地球曲率影响，假设地球为球体，通过用弧线代替直线来对两点间的距离及方位角进行精确计算；并且在计算过程中发现该方法过程较繁杂，通过对公式的一系列简化进行改进，下降其计算量。

第2节通过车载差分GPS定位，可以求得载体定位真值，即各车的经纬度，先算A载体与B载体的方位角，B载体与C车的载体解法类似。

设定求B相对于A的方位角，即A为当前位置，B为目标位置；Aj：A点经度；Aw：A点纬度；Bj：B点经度；Bw：B点纬度；

北纬为正，南纬为负；东经为正，西经为负；经纬度使用度：DDD.DDDDDD°，不采用度分秒格式(度数未加说明均采用角度制)。

R：地球平均半径；Azimuth：方位角，以真北为0°起点，由东向南向西顺时针旋转360°。

图2中A,B,C表示球面上的3个点及球面上“弧线”在该点处所夹的角；a,b,c表示A,B,C3点的对“弧”两端点与地心连线所夹的角(其实这里解释成ABC3点对弧的弧度更方便)；O为球心；L为AB两点间球面距离[15]。

图2 球面示意图Fig.2 Spherical surface schematic map

3.1 常规方法

3.1.1 相对方位角的求算

首先需要用到三面角余弦公式：

cosc=cosa·cosb+sina·sinb·
cos(A-OC-B),

(1)

式中:A-OC-B是面AOC与面BOC的二面角，即两点经度之差。

将已得AB点经纬度带入式(1)，得

cosc=cos(90-Bw)cos(90-Aw)+
sin(90-Bw)sin(90-Aw)cos(Bj-Aj).

(2)

将角c的余弦值转换成正弦值，得

(3)

将角c转换成角a需要用到球面正弦公式：

(4)

将式(3)代入式(4)，得

(5)

需要注意的是：公式得到的结果并不完全符合方位角的定义，因此要根据B相对于A的位置在4个象限2个轴上进行讨论，依据不同情况对计算结果进行不同处理。假设A点固定于原点，则

B点在第Ⅰ象限，Azimuth=A；

B点在第Ⅱ象限，Azimuth=360+A；

B点在第Ⅳ象限，Azimuth=180-A。

3.1.2 距离的求算

通过3.1.1节的计算，其中余弦值结果是可以直接用来求算AB两点间的球面距离，用反余弦函数求得c的度数，再将度数转换为弧度，乘以地球半径就得到了两点间的球面距离[16]，公式为

c=arccos(cos(90-Bw)cos(90-Aw)+
sin(90-Bw)sin(90-Aw)cos(Bj-Aj)).

(6)

将式(6)代入式(7)，得

(7)

将式(7)代入式(8)，得

L=Rc(弧度).

(8)

3.2 简化计算

3.1节推导的基于球坐标的计算公式不太适合在运算精度低的系统。结合具体标定背景，防空武器系统阵地的载体标定距离是短距离标定，因此，本文中将求坐标转换成直角坐标进行计算，再利用平面几何知识去解决。

3.2.1求算距离

设xa，ya，za为三维直角坐标下A点的坐标，B点坐标同样式，Ha为A点海拔高度，Hb为B点海拔高度，则

(9)

(10)

其中，式(9),(10)的坐标转换公式为诱导公式化简后的形式。

将式(9)和式(10)相减得

(11)

将式(11)所得差值代入勾股定理得

(12)

3.2.2 求算方位角

将经度和纬度差转化成地面距离再运用平面几何知识求解，得到方位角：

(13)

当

B点在第Ⅰ象限及y轴正半轴，Azimuth=A；

B在第Ⅱ象限，Azimuth=360+A；

B在第Ⅲ，Ⅳ象限及y轴负半轴，Azimuth=180+A。

4 算例分析

假设该防空武器系统部署在沿海丘陵地带，在武器系统进行标定时，各载体已经接收到精确的GPS定位数据，即该点的经纬度信息，通过第3节中介绍的2种标定计算方法进行解算，可以得到2种方法在随着经纬度差的增加下，距离、方位角、距离误差、方位角误差的变化值；除此之外，还得到在同一经纬度差的情况下，随着武器系统部署地海拔的提高，标定的的误差变化值。本文采用Matlab 2014a进行仿真，实验平台CPU是CORE2，内存2 G。

图3中,可以明显看出在小于几十千米的条件下，2种方法求得的2点经纬度之间的距离值曲线几乎重合在一起；同时Matlab采用详细方法计算时，平均用时为0.9 s，用简易方法运算时，平均用时0.4 s。说明在短离范围内简化算法可以替代常规算法，缩短计算时间。

图3 2种方法求2点经纬度之间的距离值Fig.3 Range value between 2 points (longitudes and latitudes) obtained with 2 methods

图4 随步长变化得到的距离误差曲线Fig.4 Range error curve obtained with variation of step size

图4中,迭代的1步长约等于1.7 m，图中的误差曲线随着距离的增加，误差缓慢上升，在短距离范围内，这些误差可以忽略不计；同时图4间接验证了图3中的2曲线几乎是重合的。

图5中,可以明显看出在小于几十千米的条件下，2种方法求得的2点经纬度之间的方位角值曲线几乎重合在一起；同时Matlab采用详细方法计算时，平均用时为1 s，用简易方法运算时，平均用时0.7 s。说明在短离范围内简化算法在计算方位角值时精度可以得到保证，运算速度也有一定的提高。

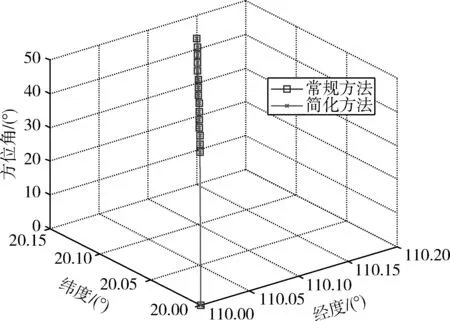
图5 2种方法求2点经纬度之间的方位角Fig.5 Azimuth angle between 2 points (longitudes and latitudes) with 2 methods

图6中,1步长约等于1.7 m，可以清楚地发现，在短距离范围内，方位角误差随着距离变大，增大趋势不明显，误差是可以忽略的。

在正常部署武器系统时，一般各载体的高度差不大，而图7中的曲线虽然在随着高度增大时，变化趋势增大，但是在高度差较小时，可以保证其精度在控制范围内。

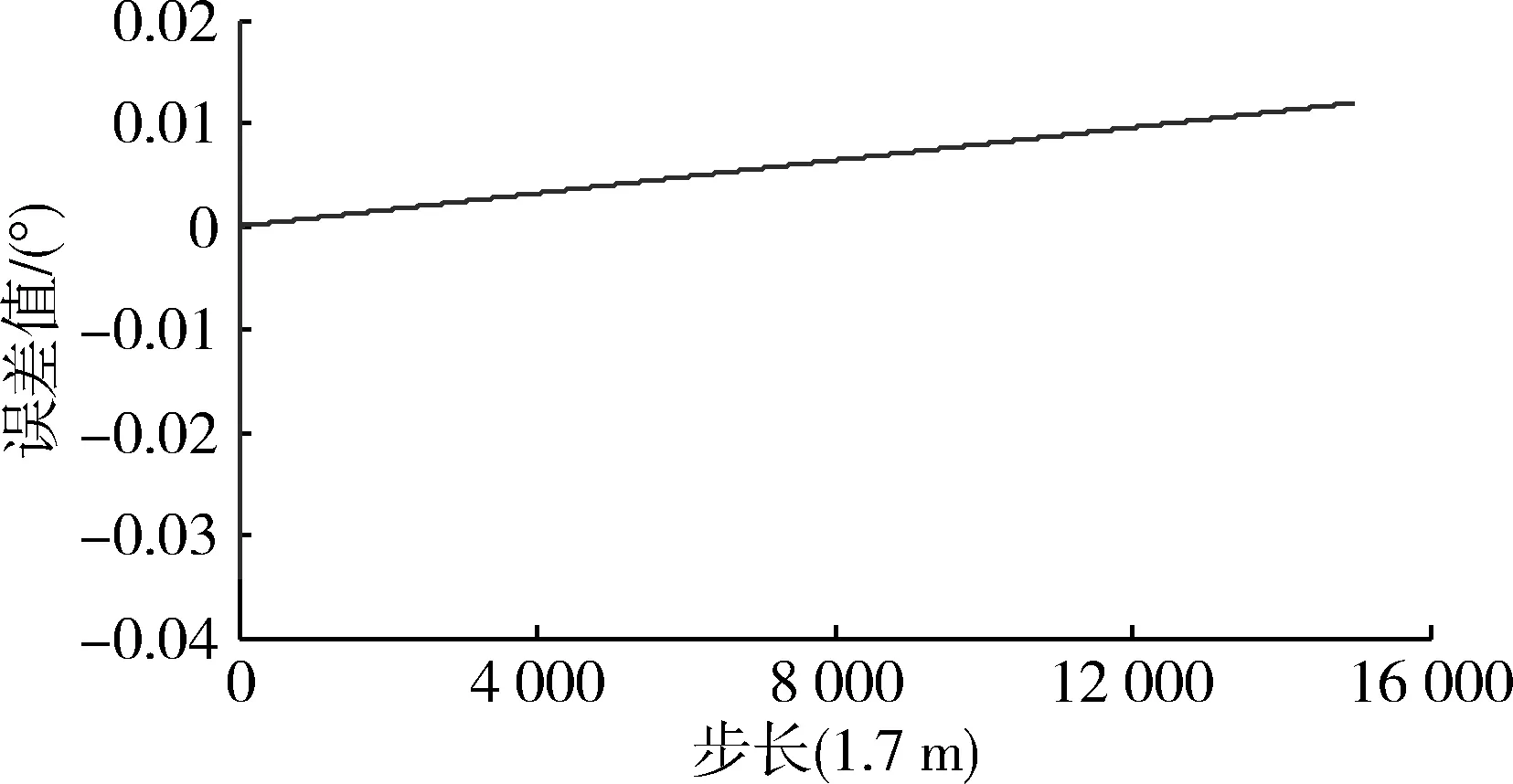
图6 随步长变化得到的方位角误差曲线Fig.6 Azimuth error curve obtained with variation of step size

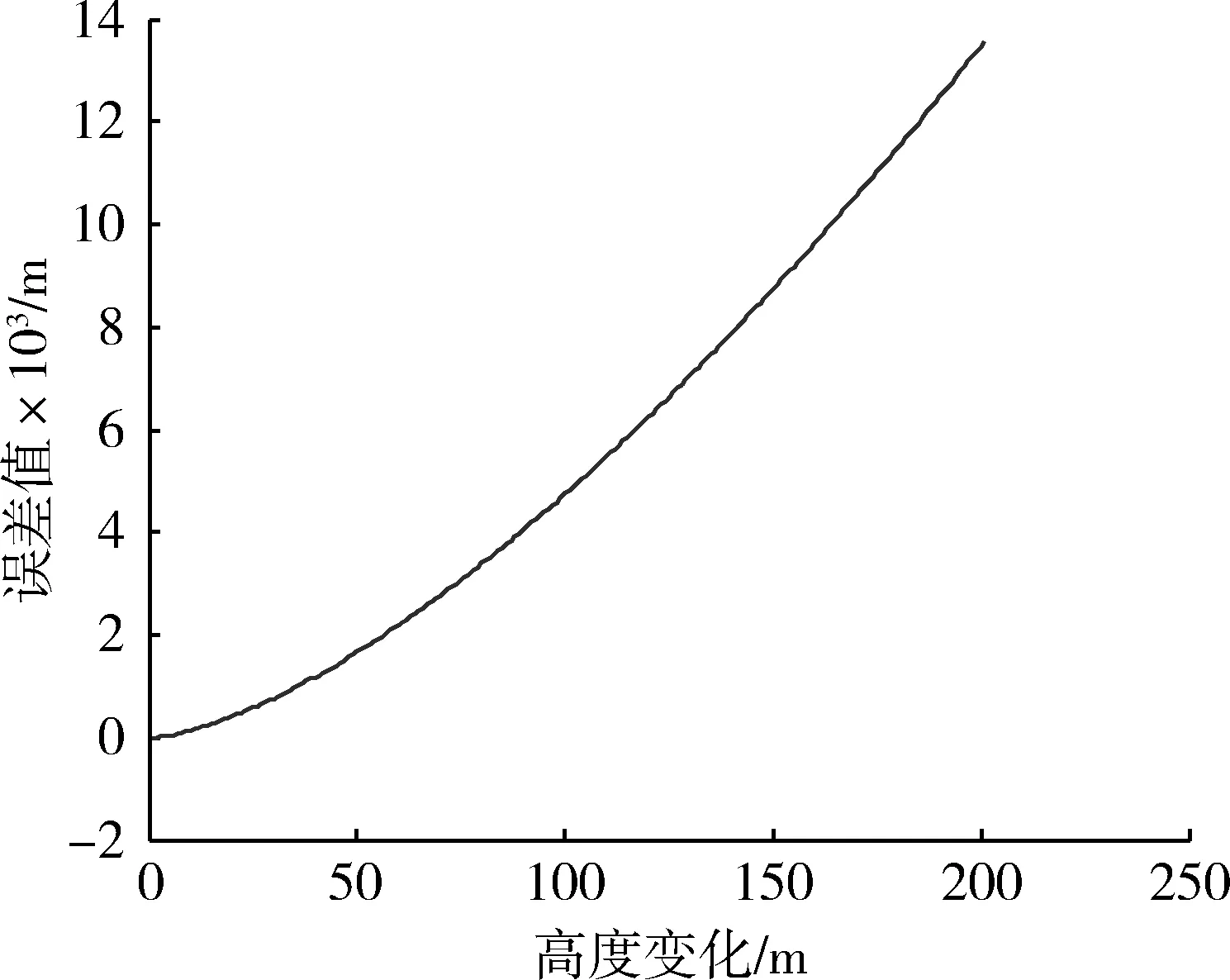
图7 随高度变化得到的距离误差曲线Fig.7 Range error curve with the variation of altitude

5 结束语

本文针对防空武器系统阵地载体标定中的不足，在对比多种标定方法下，结合具体实战背景，提出一种采用差分GPS进行标定的方法，解决了复杂地形情况下的传统标定方法受到遮挡的问题，满足并提高了了标定所需的精度；并重点介绍和推导了根据2点的经纬度求标定时的距离和方位角；在此基础上，并提出一种将以经纬度表示的球坐标转换成三维直角坐标，再利用平面几何知识去解决的简化算法。通过仿真计算作图，对比发现，简化算法在短距离的标定时具有较高的精度，两者得出的距离和方位角高度相似。因此，简化算法在短距离上可以替代常规算法。

通过计算方法的优化，运算量下降的同时，标定的时间得到缩减。在现代战争的背景下，时间对战争胜负产生巨大的影响，标定时间的缩短，意味着防空阵地的展开部署效率大大提升，给后续的目标搜索、指示、跟踪、制导留下大量时间，有效提高目标的拦截概率。