七阶球面单形-径向容积卡尔曼滤波方法*
2019-03-12赵明亮汪立新关永祥单钧麟
赵明亮,汪立新,关永祥,单钧麟
(火箭军工程大学 导弹工程学院,陕西 西安 710025)
0 引言
非线性卡尔曼滤波通过贝叶斯滤波理论转化为计算多维高斯加权的非线性函数积分。对积分的闭式解划分为对非线性函数的近似和高斯概率密度函数的近似。I.Arasaratnam等[1]基于三阶球面-径向准则提出的容积卡尔曼滤波(cubature Kalman filter,CKF)是一种基于高斯概率密度函数的近似的非线性滤波。CKF算法在高维非线性系统中能有效克服无迹卡尔曼滤波(unscented Kalman filter,UKF)等算法的滤波发散现象及粒子滤波(particle filter,PF)等方法存在的计算量大的问题,并且算法的计算复杂度仅随状态维数线性增加[2]。
文献[3]推导了三阶、五阶球面单形-径向准则,并与一般球面-径向准则形成的算法作仿真比较,仿真结果表明采用了球面单形-径向准则后,位置估计精度有明显提升;三阶CKF与五阶球面单形-径向CKF精度相近,但其均方根误差(root mean square error,RMSE)仍比较大。文献[4]推导了三阶、五阶球面单形-径向准则,仿真表明,在估计精度上五阶算法优于三阶算法及UKF算法,估计的鲁棒性也好于其他算法,但其优势不明显。文献[5]采用高阶高斯-拉盖尔多项式求解径向积分,但此种方法存在计算量大,算法设计较为复杂的缺点。
针对传统CKF算法在非线性度较高的系统估计中,存在精度低、滤波稳定性差;对于高阶径向准则,采用高斯-拉盖尔公式计算求积点及权重系数较为复杂的问题,本文使用七阶球面单形准则计算球面积分、采用矩匹配法来计算径向积分,形成七阶容积卡尔曼滤波算法。最后通过一个实际的目标跟踪问题对本文算法的有效性进行了验证。
1 非线性高斯滤波基本框架
已知非线性离散高斯系统:
xk=f(xk-1,uk-1)+wk-1,
(1)
zk=h(xk,uk)+vk,
(2)
式中:xk∈Rm为状态向量;zk∈Rm为量测向量;uk-1为输入向量;f(·)和h(·)分别为状态转移函数和量测函数;wk-1和vk为相互独立的零均值高斯白噪声,方差分别为Qk-1和Rk。
对于满足均值为0,协方差为单位阵I的高斯分布N(x;0,I)可通过如下积分规则转换式求解高斯积分:
(3)
式中:g(x)为非线性函数;I(g)为关于g(·)的高斯积分值;γi和wi分别为满足高斯分布N(x;0,I)的积分点及对应的权值;N为积分点总数;Rn为积分区域。
非线性高斯滤波基本框架为如下形式:
时间更新:
(4)
(5)

量测更新:
(6)
Pk=Pk|k-1-KkPzz,k|k-1KkT,
(7)

(8)
(9)
(10)
(11)
2 七阶球面单形-径向准则
由式(3)知,滤波器设计中必须求解高斯积分。I.Arasaratnam等人利用容积-径向变换将高斯积分转换为球面径向积分,再通过球面-径向容积准则进行积分近似[1]。
可将笛卡尔坐标的积分(3)转化为如下球面-径向坐标积分[2-5]:
(12)
此积分可以分解为球面积分S(r)和径向积分R[6-10],分别为
(13)
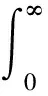
(14)
假定式(13)和式(14)由如下Ls和Lr个点的数值积分方法近似:
(15)
(16)
式中:{yi,ws,i}为计算球面积分求积点集合,Ls为相应的求积点数;{rj,wr,j}为计算径向积分求积点集合,Lr为相应的求积点数。
则I(g)可由球面-径向准则近似表示为
(17)
性质 1:当球面-径向容积准则(17)的求积点完全对称,径向积分准则只需满足偶数阶代数精度。
2.1 基于正则单形变换群的球面单形准则
采用正则单形变换群对式(13)球面积分进行计算。
定义 1:单形(simplex)是某个n维以上的欧几里得空间中(n+1)个仿射无关点集合的凸包,特指施莱夫利符号为{3,3,…,3}的正多胞形,代表考克斯特An群[11]。图1为前10维正单形的二维拓扑映射图。

图1 前10维正单形的二维拓扑映射图Fig.1 2D topology map of the first 10-dimensional positive simplex
(18)


(19)
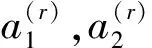
(20)

b(1)(t)= (nT)-1/2(n-t(n+1),
(21)
式中:T=2(n+1)t2-2(n+1)t+n。
设G是n上所有正多面体到自身变换的群。ga域上点的集合称为G-轨线。g包含着G群的所有变换,a是n上的不变点(即f(x)=x)。G-轨线若包含点a,则其可被定义为G(a),轨线上点的数量由a决定。
定义TnG为Tn所有到自身变换的群。Tn群的阶次为(n+1)!。群Tn的基底由以下n个不变多项式组成:
(22)

对群TnG以θ中心进行对称变换得到群TnG*。群TnG*上的不变多项式与群TnG的偶次不变多项式一致。TnG*群的阶次为2(n+1)!。超球体Sn的积分规则对群TnG*不变,且适用于所有不超过七阶的多项式。
由于积分准则需精确满足所有不大于七阶的多项式,故当n≤7时,其积分准则必定精确满足以下8个不变多项式:
因此求积点的选择至少需要8个参数。求积点依靠以下轨线来选择:
(1)TnG*(λa(1)),(2)TnG*(βb(1)),

(5)TnG*(θ),
式中:λ,β,γ为未知参数;δ为一个不为0的给定参数;a(1),b(1),c(1)由式(18),(19),(20)确定;b(1)(1/4)由式(21)确定;θ是单形Tn的中心。

综上所述,则积分准则为

(23)

和式(23)中存在9个参数,其中δ≠0为给定参数,其余8个参数D,A,B,C,E,λ,β,γ都可通过计算得到。联立式(18),(22)得到含8个未知量D,A,B,C,E,λ,β,γ的8个等式,如下所示:
(1):D+N1A+N2B+N3C+N4E=1,
(π2):r5N1Aλ2+r5N2Bβ2+r5N3Cγ2+
r1N4Eδ2/r4=(n+1)/(n+2),
(π4):r8N1Aλ4+r7N2Bβ4+r6N3Cγ4+
(π2π4):r5r8N1Aλ6+r5r7N2Bβ6+r5r6N3Cγ6+
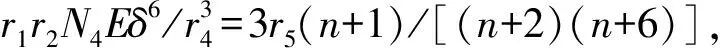
4)(n+6)],
6r5(n-1)/[(n+2)(n+4)(n+6)].
设A1=N1Aλ6,B1=N2Bβ6,C1=N3Cγ6,

(24)

2.2 基于矩匹配法的径向准则
采用数值积分方法计算径向积分式(14),得到如下等式[12-15]:
(25)
使用此种数值方法计算径向积分,其代数精度为2p+1。由球面-径向准则性质1可知,只需满足偶数阶的径向积分精度,则可使最终的球面-径向积分求积点满足对称性。令S(r)=rl,对于代数精度为2p+1的径向积分,式(25)只需对l=0,2,…,2p准确,即满足p+1个等式。满足p+1个等式中的最小求积分点数分别为(p+1)/2(p为奇数)和p/2+1(p为偶数)。
将S(r)=rl代入式(25)的左侧,可得
(26)
当p=3时,2p+1=7,此时即满足七阶径向准则,最小求积分点数为Lr=(p+1)/2=2,则只需要精确到rl的偶数阶,即l=0,2,4,6。将l=0,2,4,6代入式(26),且已知Γ(z+1)=zΓ(z)=z×(z-1)!,则可由式(25)得到:
(27)
求解上述方程组,可得径向准则求积点及其权重系数:
(28)
2.3 球面单形-径向准则
利用2.1节球面单形准则和2.2节径向准则组成球面-径向容积准则,联立式(24),(25)及式(28)并代入式(12),即构成七阶球面单形-径向容积准则为

(29)
式中:求积点数为L=4n3+6n2+6n+4。
3 仿真校验
为验证本文提出的七阶球面单形-径向容积卡尔曼滤波算法有效性,考虑如下目标跟踪问题。飞行器M在坐标系Oxyz中以一未知的角速度进行机动飞行,飞行高度h已知。忽略地球自转及扁率影响,可知飞行器旋转运动的动力学模型由如下非线性方程描述[4]:
Xk+1=Φk+1|kXk+Γk+1|kWk=
(30)
假设坐标位置为(x0,y0)的雷达对飞行器M进行跟踪,可得到雷达与飞行器M间的距离r和角度θ,则
(31)
X0=(-40 m,3 m·s-1,10 m,2 m·s-1)T,
P0=diag(4 m2,0.01 m2·s-2,4 m2,0.01 m2·s-2).
仿真结果如图2所示,分别从定性及定量角度分析。图2为飞行器位置估计的均方根误差图。由图可知,飞行器位置的估计中七阶算法明显提高了估计精度,RMSE均值分别较五阶算法提高1.58倍、三阶算法提高3.23倍;RMSE方差分别较五阶算法提高2.51倍、三阶算法提高7.86倍。具体参数见表1。
图3为飞行器速度估计的均方根误差图。由图可知,飞行器速度的估计中七阶算法明显提高了估计精度,RMSE均值分别较五阶算法提高1.58倍、三阶算法提高2.29倍;RMSE方差分别较五阶算法提高2.50倍、三阶算法提高3.84倍。具体参数见表1。

图2 位置估计的RMSEFig.2 RMSE of position estimate

表1 状态估计的RMSE均值和方差Table 1 Mean and variance of RMSE

图3 速度估计的RMSEFig.3 RMSE of velocity estimate
4 结束语
本文采用基于正则单形变换群的七阶球面单形准则计算球面积分,使用矩匹配法求积分准则计算径向积分,推导出七阶球面单形-径向容积求积分准则。通过一个目标跟踪问题进行数值仿真,仿真结果表明,本文提出的算法能有效提高非线性滤波估计精度,且具有良好的稳定性。在现实的高维复杂系统中有较好的应用前景。
