机载辐射源非合作探测杂波建模与分析*

胡蜀徽，罗昀，邱海宾，罗文波

(西南电子设备研究所，四川 成都 610036)

0 引言

以机载雷达作为辐射源的非合作探测系统，其雷达信号本身就是为目标探测而设计，所以就目标探测性能而言要优于广播、电视和全球移动通信信号的地面辐射源。除此以外，机载雷达还具有发射天线高度指向性、发射功率大、探测范围广、远程探测及预警能力强等优点。因此，机载辐射源非合作探测系统得到广泛关注[1]。

由于机载辐射源在空中运动时，发射天线处于下视工作状态，地面强杂波会给目标检测带来一系列的问题。同时杂波谱会随着机载辐射源的运动而发生展宽，造成运动目标被杂波淹没，不易于被检测[2]。此时的地杂波不再是单一特性，而是具有空时二维耦合特性[3]。需要采用空时自适应处理(space-time adaptive processing,STAP)方法抑制杂波。本文从空-地双基地的角度来分析杂波，建立了杂波的几何模型，通过仿真掌握机载雷达情况下的地杂波分布特性。最后，针对STAP方法对杂波的抑制能力进行了数值仿真，验证了STAP用于机载雷达杂波抑制上的巨大优势。

1 地杂波时-频模型与分析

1.1 地杂波时-频分布特性

机载辐射源与地面接收站双基地模式的几何关系如图1所示。

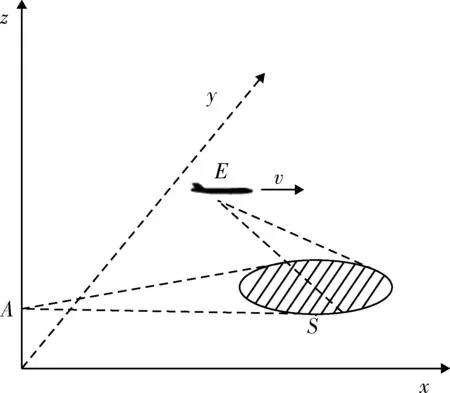
图1 双基地几何关系Fig.1 Bistatic geometry relationship

其中，E(xo,yo,zo)为机载辐射源的位置，v(vx,vy,vz)为机载辐射源的运动速度，S(xs,ys,0)为地面反射点的位置，A(0,0,za)为地面接收站的位置。辐射信号经地面反射点S反射后到达地面接收站的双基地距离为l，S点产生的回波多普勒值为fds，则等距离曲线方程[4]如下

(1)

等多普勒曲线方程如下

(2)

等距离曲线由机载辐射源和地面接收站的位置矢量决定，而等多普勒曲线则由机载辐射源的位置和速度矢量[5]决定，若取A(0,0,0.3) km，E(100,0,11) km，vE(200,0,0)m/s，等距离等多普勒曲线分布如图2所示。

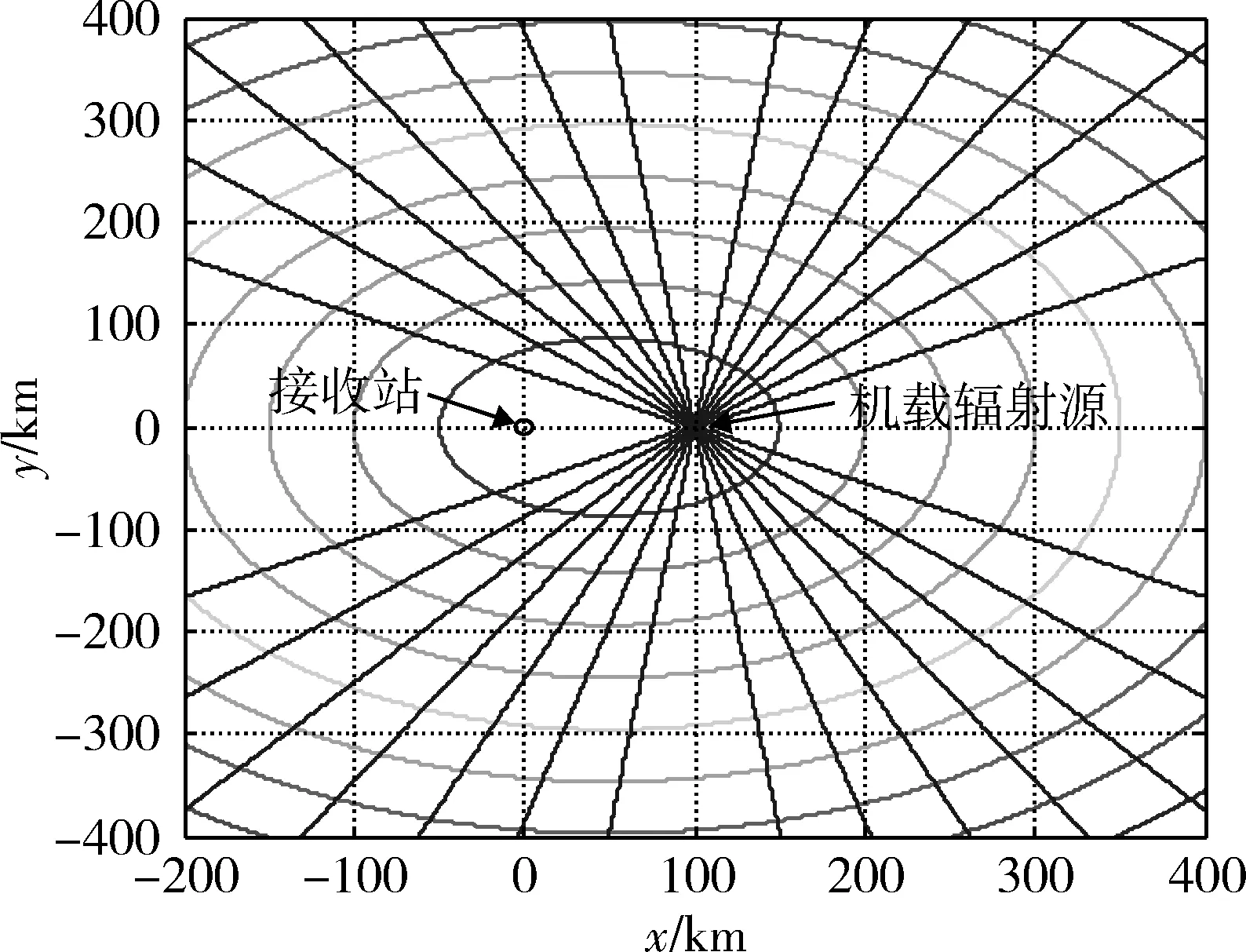
图2 等距离等多普勒曲线分布图Fig.2 Equidistance and equi-Doppler curve distribution

由图2可以看出，等距离曲线为椭圆曲线，等多普勒曲线为双曲线。当机载辐射源对地面进行照射时，其波束总是覆盖了一定的距离-多普勒区域。由此可知，目标在距离维度上是被杂波淹没，当主波束照射到目标时，主瓣杂波与目标回波会同时在时域上出现[6]，而当目标运动速度不高时，在多普勒域上目标也容易被杂波覆盖。

1.2 阵列天线接收时地杂波模型

地面等距离曲线方程如下

(3)

将其转化为极坐标形式，可得

(4)

可以得到空域角频率的极坐标形式

(5)

式中：φ为地面辐射点相对于接受天线轴的方位角；θ为地面散射点与接收机连线的俯仰角。

回波多普勒频率为

(6)

式中：Res为机载辐射源到达地面反射点的距离。

(7)

(ye-ys)vy+(ze-zs)vz].

(8)

时域多普勒频率的极坐标形式

(y-ρsinφ)vy+zevz].

(9)

根据想定的预警机雷达工作参数，发射信号频率为600 MHz，脉冲宽度为13 μs，脉冲重复频率为300 Hz，脉冲个数为16，扫描方式为机械圆周扫描，飞机的巡航速度为120 m/s，巡航高度为12 km。设地面接收站A的位置为(0,0,0.3) km，接收天线阵元数为8，阵元间距d=λ/2，机载辐射源E的位置为(110,100,12) km，双基地距离分别为400,500,600 km，不同辐射源速度v的条件下，空时曲线如图3所示。空时曲线的形状取决于载机的速度矢量，空时曲线的大小取决于双基地距离l。

如图4所示，当双基地距离的值分别为1 000,1 050,1 100 km时，3个相邻距离门的空时曲线近似重合。这说明在近距离情况下相邻距离门杂波的分布特性具有快速变化特性，而在远距离情况下相邻距离门杂波的分布特性具有近似独立分布特性[7]。

从图3中可以看出,近距离单元相邻距离门杂波扩展严重，若直接对杂波进行空时自适应处理，得到的杂波抑制滤波器的凹口较宽，抑制能力也不够，不仅不能有效抑制强杂波，而且会将慢速弱目标信号滤除[8]，导致目标检测盲区的范围扩大，所以需要对不同距离单元的近距离杂波进行速度补偿。

1.3 杂波子空间分析

杂波子空间分析的主要目的是掌握杂波自由度特性。设第k个距离环对应的杂波子空间为Θ，在单基地机载正侧视天线阵情况下，当满足ws(Φ,θ)=wt(Φ,θ)时

dim(Θ)=M+N-1，

(10)

式中:M为天线阵元个数;N为发射信号的脉冲个数；dim表示杂波子空间的维度。

在双基地条件下，ws(Φ,θ)，wt(Φ,θ)之间存在着非线性关系，相对于线性情况下杂波自由度有所增加[9]，总的杂波自由度满足如下表达式

dim(Θ)≥M+N-1.

(11)

为了了解杂波自由度的变化情况，对不同双基地距离条件下的杂波自由度进行仿真。设发射信号脉冲个数为16，载机飞行速度为(0,120,0) m/s，接收天线阵元个数为 8，双基地距离分别为500,700,900 km，仿真结果如图5所示。

从图5可以得到杂波协方差矩阵特征值数目随特征值变化的关系。当特征值大于10 dB时特征值个数都在 30～36之间[10]，即杂波的自由度约为30～36，大于23(即M+N-1)。空时协方差的最大自由度[11]为MN-1=127，当杂波的自由度小于MN-1时，用最优处理器就可期望获得优异的杂波抑制效果。

1.4 杂波谱分布

在双基地条件下，地杂波能量呈现出在方位-多普勒域上的空时耦合特性。设有M元等间距线阵，一个相干处理间隔内的脉冲数为N，将第m列第n个脉冲的接收数据记为xmn，第n个脉冲的阵列数据矢量Xs(n)为

图3 不同速度矢量条件下的空时曲线Fig.3 Space-time curve under different velocity vector conditions

图4 远距离空时曲线Fig.4 Long distance space-time curve

图5 杂波协方差矩阵的特征值Fig.5 Clutter covariance matrix eigenvalue

Xs(n)=(x1n,x2n,…,xMn).

(12)

将Xs(n),n=1,2,…,N排成MN的列矢量X，即

(13)

式中：X为距离单元上的一个空时快拍;R=E(XXT)为距离单元上的杂波协方差矩阵。

空时二维导向矢量s的表达式[12]为

(14)

式中:⊗表示Kronecker直积;φs(ψs)，φt(fd)分别为空域导向矢量和时域导向矢量。对杂波协方差矩阵R的变量(ws,wt)在相应的取值区间内进行遍历就可以得到二维杂波功率谱[12]，其表示式为

(15)

仿真参数如下，地面接收站的位置为(0,0,0.3) km，机载辐射源的位置为(110,100,12) km，飞行速度为(0,120,0) m/s，双基地距离为600 km，信号脉冲个数为16，接收天线阵元数为8，杂波空时二维谱分布仿真如图6所示。

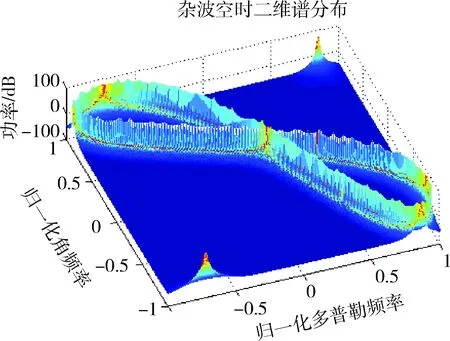
图6 杂波空时二维谱分布图Fig.6 Clutter space-time spectral distribution

3种不同速度矢量条件下的杂波功率谱分布如图7所示，功率谱在二维平面与图3中的空时曲线一致。杂波的二维谱分布特性取决于杂波的空时关系，空时关系由机载辐射源和接收站的几何关系决定[13]。所以，为了准确掌握杂波功率谱的分布特性需要获得辐射源的位置和运动参数信息。

2 空时自适应滤波算法分析

2.1 空时自适应算法结构

STAP处理器的基本原理是对全部M个天线通道上的每个延迟抽头分别计算和应用一个自适应权值，抽头个数为一个相干处理间隔内的脉冲数N。所以自适应处理器的权矢量为M×N，其处理结构[14]如图8所示。

假设目标的空间频率和多普勒频率分别为fst和fdt，空时导向矢量s为

s=ss⊗st,

(16)

式中：ss为目标的M维空域导向矢量；st为目标的N维时域导向矢量，分别表示为

ss=(1,ej2πfstT,…,ej2π(M-1)fstT)T,

(17)

st=(1,ej2πfdtT,…,ej2π(N-1)fdtT)T,

(18)

式中:fst=(d/λ)sinθt，d为接收天线间距，λ为发射信号波长，θt为目标方向。为检测第k个距离单元回波数据xk中是否存在目标信号，让其通过一个权值为wk的空时滤波器，滤波器的输出为

(19)

STAP处理可以表示为

(20)

wopt=μR-1s，

(21)

2.2 STAP处理后的杂波谱频响

对STAP处理器的空时响应进行仿真，仿真参数为:地面接收机的坐标为(0,0,0.3) km，机载辐射源的坐标为(150,100,12) km，载机的运动速度为(0,120,0) m/s，经过地面反射点S的双基地距离为500 km，目标的速度矢量为(110,100,0) m/s，经过目标反射后的双基地距离为700 km，发射信号脉冲个数为16，接收天线阵元个数为 8。由图9可知，空时响应的主瓣对准目标位置，在杂波的空时分布位置上形成了凹口，可同时抑制主瓣杂波和旁瓣杂波。

图9 STAP处理后空时响应图Fig.9 Space-time response graph

图10是目标所在位置的方位响应与多普勒频率响应图。在目标方位上的多普勒频率响应可以区分来自相同方向上的目标和杂波。而目标多普勒频率处的空域响应表示空间波束形成，对杂波存在的方位上进行抑制形成零点[15]，因此可以区分具有相同多普勒频率的目标和杂波。

图10 多普勒频率响应与空间频率响应Fig.10 Doppler frequency response and space frequency response

2.3 信杂噪比改善因子

对于空时自适应处理，信杂噪比改善因子(improvement factor)是评判STAP处理器对杂波抑制性能的重要尺度。当权矢量满足wopt=μR-1s时，处理器性能最优即输出信杂噪比最大，可以简化为

(22)

设发射信号脉冲个数为16，接收天线阵元个数为 8，输入杂噪比CNR为30 dB，信杂噪比改善因子仿真如图11所示。

图11 STAP处理的信杂噪比改善因子Fig.11 SINR improvement factor under STAP processing

图11给出了STAP处理器的信杂噪比改善因子。在杂波谱中心的多普勒频率上得到了50.7 dB的信杂噪比改善因子，同理近似信杂噪比改善因子IFopt=CNR+10lg(MN)=51 dB极其接近。

由图11可知，在双基地模式下，信杂噪比改善因子在多普勒频率维上出现了2个极小值。由此可得，在某些方位上，极值凹点处多普勒频率所对应的目标难以检测[16]。即当目标与杂波在空、时、频域都重合的情况下，无法被有效区分。

3 结束语

本文建立了机载辐射源非合作探测杂波模型，通过对杂波的几何关系分析得出了杂波的时频分布特性。并且分析了在不同辐射源的速度矢量下的空时曲线特性，得出了近距离情况下杂波具有快速变化特性，而远距离情况下相邻距离门杂波具有近似独立的分布特性。通过对杂波谱的建模仿真，证明了杂波与目标信号在空时频域可分的结论，同时还分析了杂波谱分布与双基地几何配置之间的关系。最后给出了空时自适应STAP处理算法流程，并仿真得到了空时响应结果，验证了STAP处理对杂波抑制的有效性。