一种散乱点云的精准重建方法

刘阳阳,李仁忠,刘哲闻,张缓缓

(西安工程大学 电子信息学院,陕西 西安 710048)

0 引 言

为了提高对点云数据[1]的重建质量,使得点云重建更接近于真实情况,文献[2]对点云数据用VoxelGrid(体素化栅格)创建一个k邻域的三维体素栅格对点云进行精简,该方法可以在保证点云特征的前提下,大大提高重建速度,但是重建得到的网格并不光滑,重建效果和现实有一定的偏差。对重建得到的网格进行平滑,可以使模型更接近于现实模型,LAPLACIAN[3]平滑因使用便捷,对网格的平滑速度快,而得到了广泛的应用,但是拉普拉斯对网格的平滑往往会导致网格的局部收缩,迭代次数越大,收缩越明显。TAUBIN[4]结合了数字信号处理方面的知识来优化拉普拉斯算法,使用一个负收缩因子μ将拉普拉斯平滑造成的收缩再放大回去,该方法可以在一定程度上将拉普拉斯迭代平滑引起的收缩放大,从一定程度上减少了因迭代次数过多引起的失真,但是时间运行成本有所增加。后来陆续有人提出对点云数据进行光顺拟合,以达到最终获取光滑的重建表面的要求,这对得到光滑的三维重建提供了一个新思路．由于点云模型的离散性,无法提供一个关于点云表面光滑的数据定义,通常将点云的局部拟合表面定义为近似曲面。在此思想上,移动最小二乘(MLS，moving least squares)的概念最先由LEVIN[5]提出,通过采用局部高阶多项式为一组给定的离散采样点提供一个逼近的插值曲面。ALEXA等[6]首次将其应用到点云模型上,从距离当前采样点较近的邻近点开始检索,并把它们投影到当前采样点附近的拟合表面多项式上,之后,陆续有人对MLS进行了改进[7-9]。大部分的改进需要对点云重新构造一个局部参考表面,但是很难在当前检索点附近找到一个合适的参考平面对点云进行重新投影,对于密度较低的点云,获取合适参考平面的难度更大。在实践中,对于确定参考平面的邻域点,一是可以通过计算测试点与邻近点之间的欧几里德距离,进而得到阈值内的邻域点[10]。另一个解决办法是找到当前检索点的k近邻,然后计算k邻域平均值[11]。但这些方法中的噪声因素容易对近邻点的计算造成误差[12],进而对建立局部参考平面产生影响。

本文给出的基于加权协方差矩阵的方式计算局部参考平面,对于不同距离的邻域点设置不同的权值,减小噪声点的影响,实验结果表明该方法可以有效获取高质量的流形点云,对重建网格中的空洞也有一定的修补能力,重建结果的平滑程度高于对网格局部平滑后的处理,重建结果更接近于现实。

1 算法原理

在对点云进行重建中,先通过统计滤波对原始点云进行大尺度去噪,然后使用体素栅格精简去除冗余数据,且可以在保持点的局部特征下加快重建速度,但精简后的数据依然会存在局部空洞、细小噪声和误差等问题[13-14],对精简过的数据直接重建,得到的重建表面并不光滑,且存在局部空洞。如果对重建表面进行局部网格平滑[15],可以一定程度上改善重建网格的光滑程度,但效果并不理想,且对网格平滑并无法修复重建表面的空洞,因此,本文在对点云进行初步去噪[16-17]和使用体素栅格进行精简后,采用MLS对点云数据进行预处理,并提出采用加权的协差矩阵来计算局部参考平面,获取高质量流形点云,最后利用多准则局部投影三角化对点云进行快速网格化,进而实现高质量的曲面重建。

MLS的基本思想是采用迭代的投影方式，通过将分布在采样表面周围的点移至拟合表面上来消除噪声,获得光滑的流形表面，如图1所示。首先,为查询点p找到一个局部参考平面H,q为p在H上的投影(红点),利用H计算一个局部拟合曲面g,p到g上投影点(绿点)为最终的点。

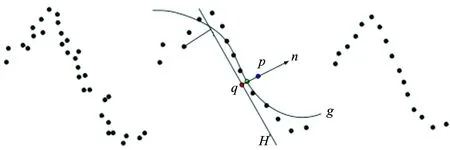
图 1 算法原理Fig.1 Schematic diagram of algorithm

1.1 计算局部参考平面H

(1)

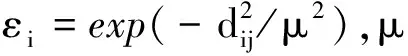
采用这种加权方式，根据邻近点距当前检测点距离的不同，进而设置不同的权值，根据设置的距离的阈值，将小于距离阈值的邻近点，作为邻近点加权的重要点，对其设置较大的权值；在距离阈值范围外的点，根据距当前检测点距离的远近设置不同的权值，距离越远，占的权值比重越小。采用加权协差方阵计算参考平面可以从一定程度上抑制噪声，不仅将距离检测点较近的邻近点考虑在内，还考虑到了距离较远的邻近点的影响，对于点云中较尖锐的部分，也能进行正确的法线估计。

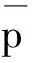
H={x|〈e0,x-p〉=0,x∈R3}

(2)

1.2 局部拟合曲面g

局部拟合曲面，可以通过二阶多项式(3)得到:

g(u,v)=Au2+2Buv+Cv2+Du+Ev+F

(3)

二阶项式的系数由式(4)得到:

(4)

式中：(ui,vi) 为pi在参考平面H上的投影坐标;fi为pi到平面H的垂直高度; 权重函数θ(d)=exp(-d2/h2)， 其中d为近邻点与投影点q的距离，h为设置的高斯系数， 数值越小， 点被平滑的程度越高。

1.3 获得最终的投影点

由二元多项式可求投影点q的局部坐标，进而可得平滑后采样点的坐标。利用局部点云质心建立局部坐标系，并向MLS曲面投影产生新的顶点。

2 结果与分析

本文采用的实验平台 Intel Core i5-6400 CPU@2.70 GHz，内存8 GB,Window10 64 位操作系统，Visual Studio 2013 Visual C++win32 控制台应用程序，开源点云库 PCL1.7.2.采用微软 Kinect 2.0[19]视觉传感器[20]，以扫描获取的实物人台模型三维点云模型数据为研究对象。图2～4，图5～7分别为将0°和45°人体模型的体素栅格边长设为 0 cm,1 cm,1.5 cm 精简后，对点云直接重建，对点云重建后进行 Taubin 网格平滑，以及在精简后对点云经过 MLS 平滑处理后再重建的效果图(统计结果见表1～4)。表1和表3分别为对0°和45°人体模型对重建过程中预处理阶段阶段所需的时间和网格化所需的时间进行了统计， 表2和表4分别对 0°和45°人体模型对两种平滑算法平滑时间和平滑后重建片面数量进行了统计。

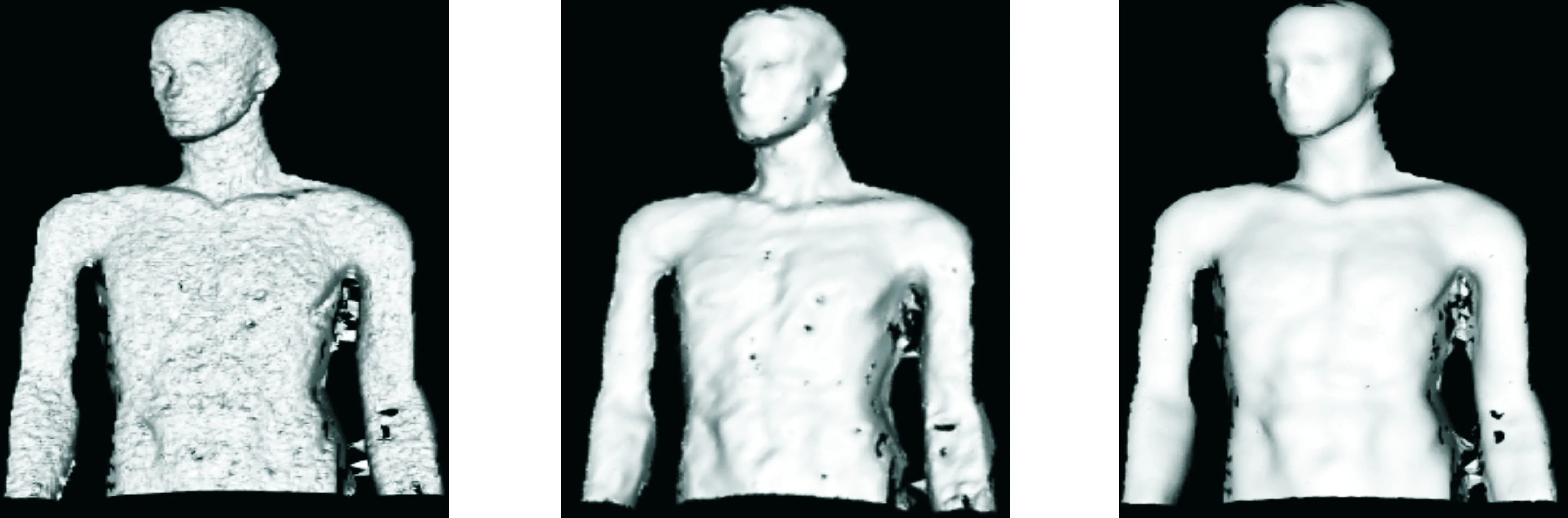
(a) 三角化重建结果 (b) Taubin平滑结果 (c) 经 MLS后三角化结果图 2 0°人体模型的原图重建Fig.2 Reconstruction of the 0° mannequin

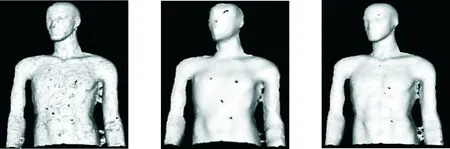
(a) 三角化重建结果 (b) Taubin平滑结果 (c) 经 MLS后三角化结果图 3 0°人体模型的1 cm重建Fig.3 1 cm reconstruction of the 0° mannequin

(a) 三角化重建结果 (b) Taubin平滑结果 (c) 经 MLS后三角化结果图 4 0°人体模型的1.5 cm重建Fig.4 1.5 cm reconstruction of the 0° mannequin

体素栅格长度/cm精简后的点云数精简时间/msMLS处理时间 /ms重建时间/ms体素栅格长度/cm精简后的点云数精简时间/msMLS处理时间 /ms重建时间/ms028 164041 5089 5351.52 373776881 2951.04 988841 9232 377

表 2 0°时两种平滑算法的比较

(a) 三角化重建结果 (b) Taubin平滑结果 (c) 经 MLS后三角化结果图 5 45°人体模型的原图重建Fig.5 Reconstruction of the 45° mannequin

(a) 三角化重建结果 (b) Taubin平滑结果 (c) 经 MLS后三角化结果图 6 45°人体模型的1 cm重建Fig.6 1 cm reconstruction of the 45° mannequin

(a) 三角化重建结果 (b) Taubin平滑结果 (c) 经 MLS后三角化结果图 7 45°人体模型的1.5 cm重建Fig.7 1.5 cm reconstruction of the 45° mannequin

体素栅格长度/cm精简后的点云数精简时间/msMLS处理时间 /ms重建时间/ms体素栅格长度/cm精简后的点云数精简时间/msMLS处理时间 /ms重建时间/ms026 127070 56210 5351.51 9092128495241.03 9912872 7641 759

表 4 45°两种平滑算法的比较

在0°人体模型试验的效果图中，图2(a)为对点云直接进行三角投影重建，图2(b)为对重建的结果进行Taubin平滑，图2(c)为经MLS处理之后的三角化重建的结果，经MLS处理后有效地消除了身体上的小空洞，对胳膊处相对较大的空洞修补不明显，重建效果相较图2(a)，3(b)更为光滑，图3经1 cm精简后的重建中，经MLS平滑后重建的结果，局部特征保持相比Taubin平滑的结果更加逼真，且MLS表现出对局部空洞良好的修复能力，此时Taubin平滑相比于经MLS平滑处理，模特脸部的特征重建失真已经较为严重，图4经1.5 cm精简后重建，Taubin平滑和经MLS处理都对空洞进行较为有效的处理，但是经MLS处理后的重建，不仅保持重建的光滑性，重建特征更加优良，重建的效果更接近现实；在45°人体模型的实验效果图中，从图5(a)直接对点云进行重建的效果图中看出，边界噪声对重建效果影响较大，图5(b)经Taubin平滑由于边界噪声导致重建的不光滑得到的一定的改善，但图5(c)经MLS处理后的重建，对边界噪声的抑制明显优于Taubin平滑，图6(c)经MLS处理，有效修补模特身体左侧的大部分空洞，重建效果相较于Taubin处理更加光滑，MLS依然表现出对边界噪声良好的抑制能力，在图7的1.5 cm精简后的重建中，图7(c)经MLS处理后，模特脖子处的空洞被消除，对身体中间部分的空洞修补不明显。从表1和表3的时间上比较，相对于三角网格化的时间，在对点云进行体素栅格精简和MLS平滑处理需花费更多的时间，但是预处理结果直接影响着最终的网格重建。在表2和表4中，通过对分别经Taubin和MLS两种算法处理后，得到重建片面数目进行统计，片面总数相差不大。

3 结 语

在网格重建过程中控制片面数目基本相同的情况下， 后期经过 Taubin 平滑后， 虽然可以改善局部的不平滑， 且随着精简边长的增大， 点云数量减少，但 Taubin 平滑的结果越来越失真， 且无法有效地消除漏洞。而通过 MLS，利用加权协方差矩阵鲁棒估计局部参考平面，进而得到更精确的法线估计。对于点云的局部空洞有着较好的修补，边界噪声也得到有效的抑制，通过获得平滑的流形面，显著提高网格重建的质量，使得重建结果更加接近于现实。 从实验结果看出， 通过MLS光滑得到流形表面相比 Taubin 平滑可以更好地提高网格重建的质量， 但是 MLS 相较于 Taubin 平滑的时间成本更高一些， 如何缩短MLS获取流形面的时间是下一步的工作重点。