一种基于羊角曲线的加工轨迹G2连续光顺方法
2019-03-08李文森管声启
李文森,管声启,郑 璐,梁 洪
(1.西安工程大学 机电工程学院,陕西 西安 710048;2.西安交通大学 机械工程学院,陕西 西安 710049)
0 引 言
随着制造业迅速发展,零件的几何形状越来越复杂。但是大部分的数控系统难以有效处理此类参数形式的加工轨迹,一般通过CAM软件生成连续小线段(G01命令)逼近加工轨迹[1]。由于在相邻线段构成的拐点处切向不连续,机床在执行这些指令时需要将速度降低到零。这种频繁的加减速会增加加工时间和引发机床的振动,同时也降低了工件表面加工质量[2-3]。因此,为了提高工件质量及加工速度,必须对加工轨迹有效规划。
为了改善线性加工轨迹的光滑性,许多学者提出了轨迹光顺技术,包括全局光顺技术和局部光顺技术[4-5]。全局光顺技术通过高阶参数曲线拟合或插值连续小线段来改善原有加工路径,如B样条曲线或NURBS[6-7]。然而,由于轨迹长度计算繁琐[8],进给波动无法抑制[9-10],使实时插补成为困难。局部光顺技术用微小曲线替换相邻直线的拐角部分,实现运动的连续性。随着高阶参数拟合技术的发展和此类方法计算的便捷性,局部光顺技术越来越受到学者的关注。司慧晓[11]用圆弧过渡拐角,但是圆弧只能实现C1连续。YUTKOWIZ[12]和ZHANG[13]提出用高阶多项式混合过渡拐角,但是迭代方法确定多项式系数非常耗时。PATELOUP[14]采用8个控制顶点的3次B样条来光顺拐角,无法解析计算曲率极值。SHI[15]和FAROUKI[16]介绍了PH(Pythagorean Hodograph)曲线局部光顺拐角的方法,控制点的确定需迭代优化。FAN[17]和SENCER[18]分别用4次和5次Bézier曲线过渡光顺拐角,曲率极值可解析确定。
尽管众多研究方法能够实现对拐角处的光顺, 实现连续的加工曲线。 但是, 存在以下问题尚未解决: 拐角处连接曲线的弧长需牛顿-辛普森迭代获得;
精细插补产生的位移增加量需返回迭代。 这些问题会占用 CNC 系统的计算内存, 使实时性变差。本文提出一种基于羊角曲线的过渡曲线光顺方法, 能够实现加工轨迹的G2连续、 轮廓误差可控和光顺速度非零的效果。 同时光顺曲线的长度可解析获得, 精细插补的位置增量基于多项式计算, 效率更高。
1 几何光顺
羊角曲线的曲率值随螺旋线长度线性增加,且具有G2连续性质,见图1。由于其优良特性,被广泛应用于公路设计和机器人运动轨迹设计中。
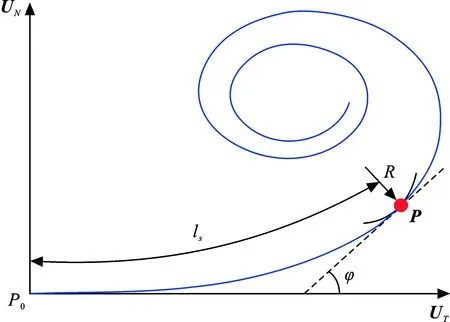
图 1 羊角曲线Fig.1 Clothoid curve
文献[19] 对图1 所示任意羊角曲线P(φ)={X(φ),Y(φ),Z(φ)} 的几何特征进行了解释, 其结论为
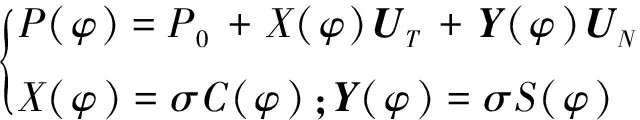
(1)
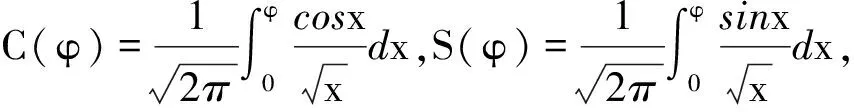
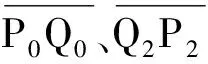
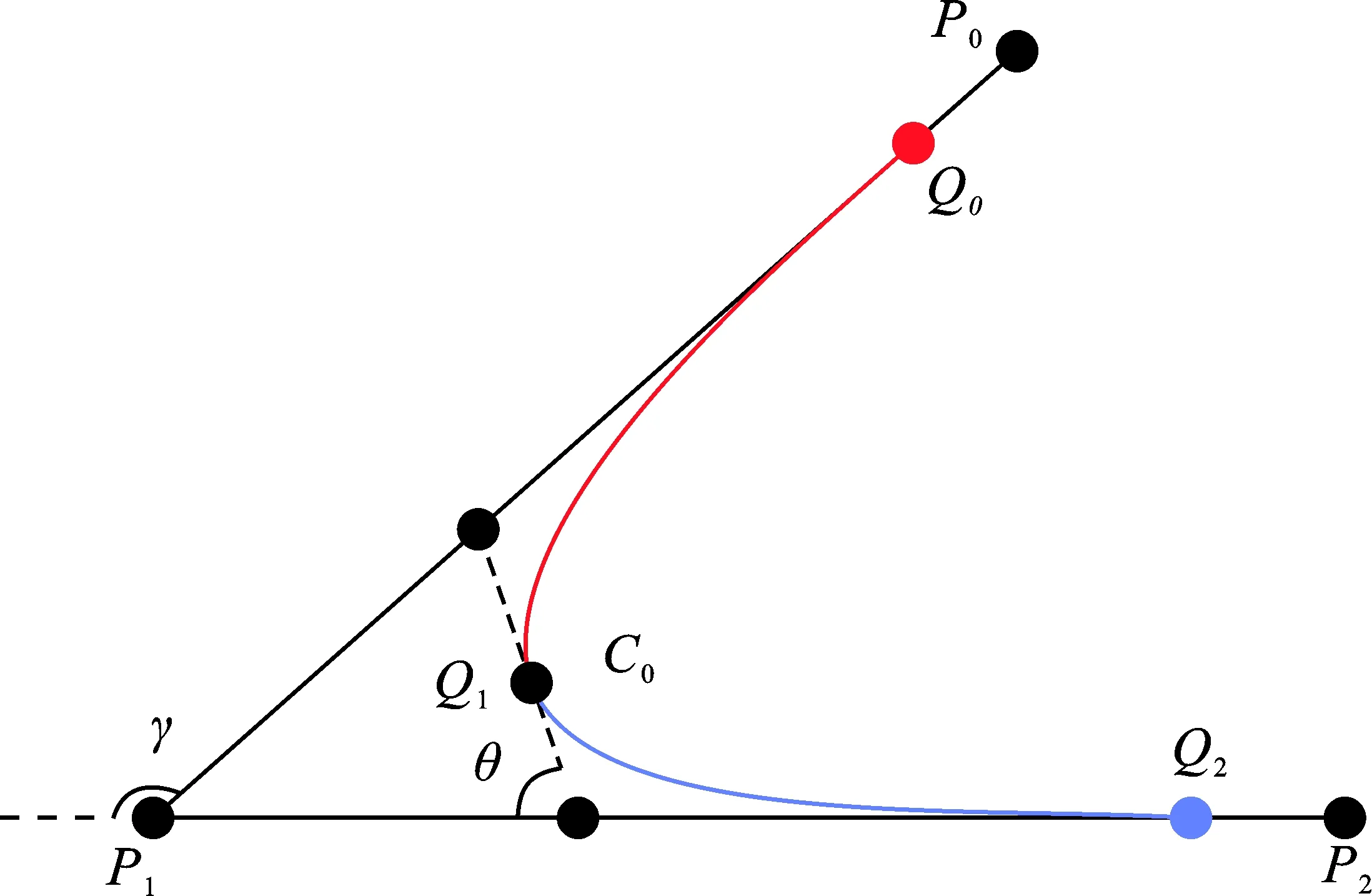
图 2 羊角曲线光顺实例Fig.2 Example of clothoid smoothing
1.1 G2连续性
1.2 轮廓误差
轮廓误差是光顺曲线与原线性轨迹之间垂直于曲线切线的间距。显然光顺曲线相接处为轮廓误差极值,也是光顺曲线最大曲率所在位置,见图3。如图3所示,轮廓误差ε可以表示为
(2)
由式(2)可知,轮廓误差可以通过光顺直线长度lt控制,因此在预定的最大轮廓误差εp约束下的光顺直线长度lt为
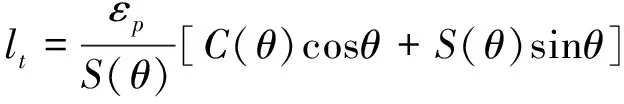
(3)
1.3 光顺直线长度
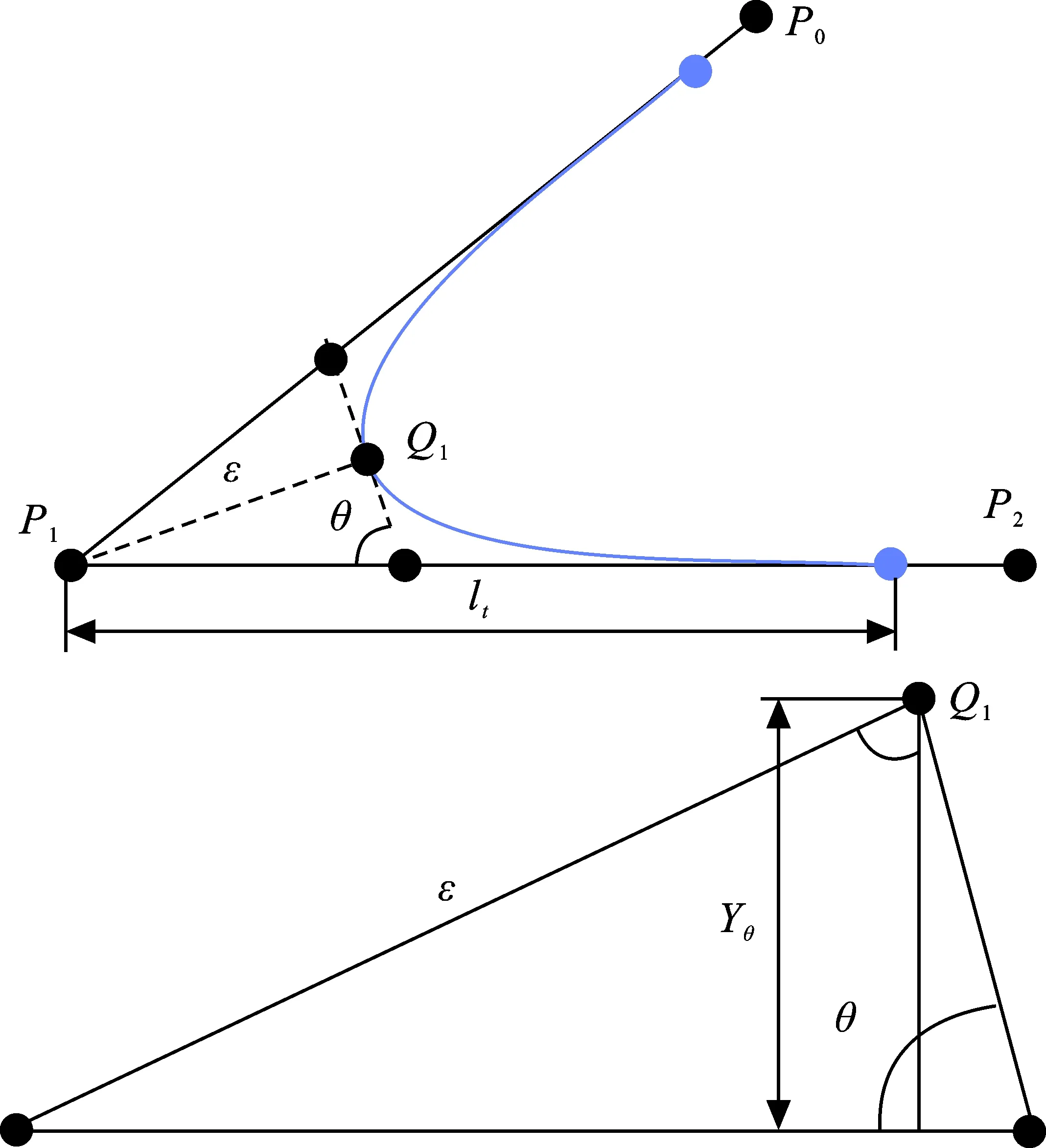
图 3 羊角曲线轮廓误差Fig.3 Approximation error of clothoidcurve
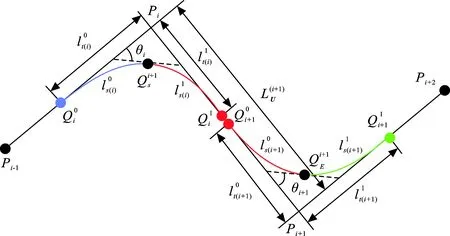
图 4 连续线段羊角光顺Fig.4 Clothoid smoothing of continuous segment
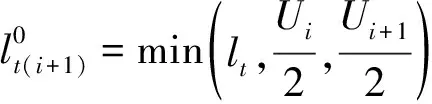
(4)
此时,光顺曲线的长度为
(5)
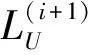
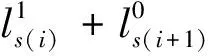
(6)
2 速度规划及插补
为了将光顺算法嵌入到CNC系统中,除了几何光顺算法之外,还需通过速度规划和实时插补才能实现。速度规划包含双向看单元和速度规划单元。双向看单元即为双向查看光顺的混合加工轨迹,在运动学和动力学条件约束下得到速度敏感点的速度极值;速度规划单元根据速度极值实行加减速规划,从而得到连续稳定的加减速。实时插补根据生成的速度曲线计算位置增量并作为位置参考指令发送给各运动轴。
2.1 速度规划
首先对光顺后的加工轨迹进行双向查看,以获得曲率极值点(速度敏感点)的允许速度。曲率极值为光顺曲线对的连接点,利用曲率计算公式可计算出曲率极值。结合法向/切向加速度(AN/Amax)、法向/切向跃度(JN/Jmax)和弓差等确定速度敏感点速度。双向看策略分为2个部分。
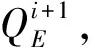
(vJE-vs)3+4vs(vJE-vs)2+
(7)
式中:vJE和vs分别代表每个单元切向跃度约束下的末速度及初速度,Jmax为切向跃度。根据公式(7)求出vJE,考虑到切向加速度、弓差极值δmax、曲率及法向运动的约束,逆向看末速度还应该满足:
(8)
式中:Ts为采样时间间隔。此时的末速度即为下一个单元序列的初速度,循环公式(7)和(8),完成逆向看速度扫描。

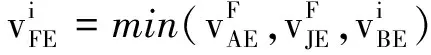
(9)
双向看策略之后, 速度敏感点的速度都已求得, 从而获得整段刀具路径的速度约束。为实现精细插补计算, 有必要将速度约束与位移结合起来, 利用文献[21]中的S加速法得到连续光滑的速度-时间曲线。
2.2 插补算法
插补算法是利用速度规划出的速度极值来确定某一采样时间Ts的位移量及插补点坐标。由于混合加工轨迹中包含线性段和曲线段插补,因此根据插补点的位置在线性段或者曲线段来分别计算。混合加工轨迹如图5所示,当插补点I(kTs)位于线性段,插补算法如下:
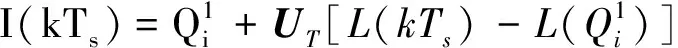
(10)
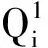
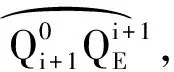
S(θi+1)UN]
(11)
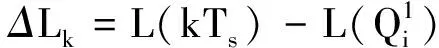
(12)
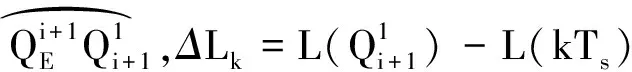
S(ΔLk)UN]
(13)
最终获得的位置指令被输送给运动控制器,进行反馈控制。
3 结果与分析
为验证羊角光顺算法的可行性,本文对UGNX生成的连续小线段蝴蝶图形进行光顺,并设置参数:最大进给速率F为20 mm/s,最大切向/法向加速度Amax为200 mm/s2,最大切向/法向跃度Jmax为3 000 mm/s3,轮廓误差εp为50 μm,最大弓差为5 μm,采样时间Ts为1 ms。该仿真算法在MATLAB环境中实现。
首先,如图5(a),将光顺算法应用在蝴蝶图形线性加工轨迹的拐角处。图5(b)为放大黑色小方框后的图像,不难看出详细光顺轨迹。
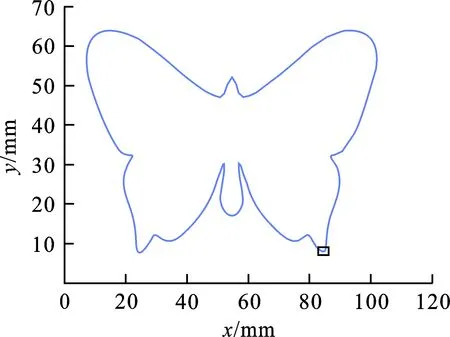
(a) 蝴蝶线性轨迹
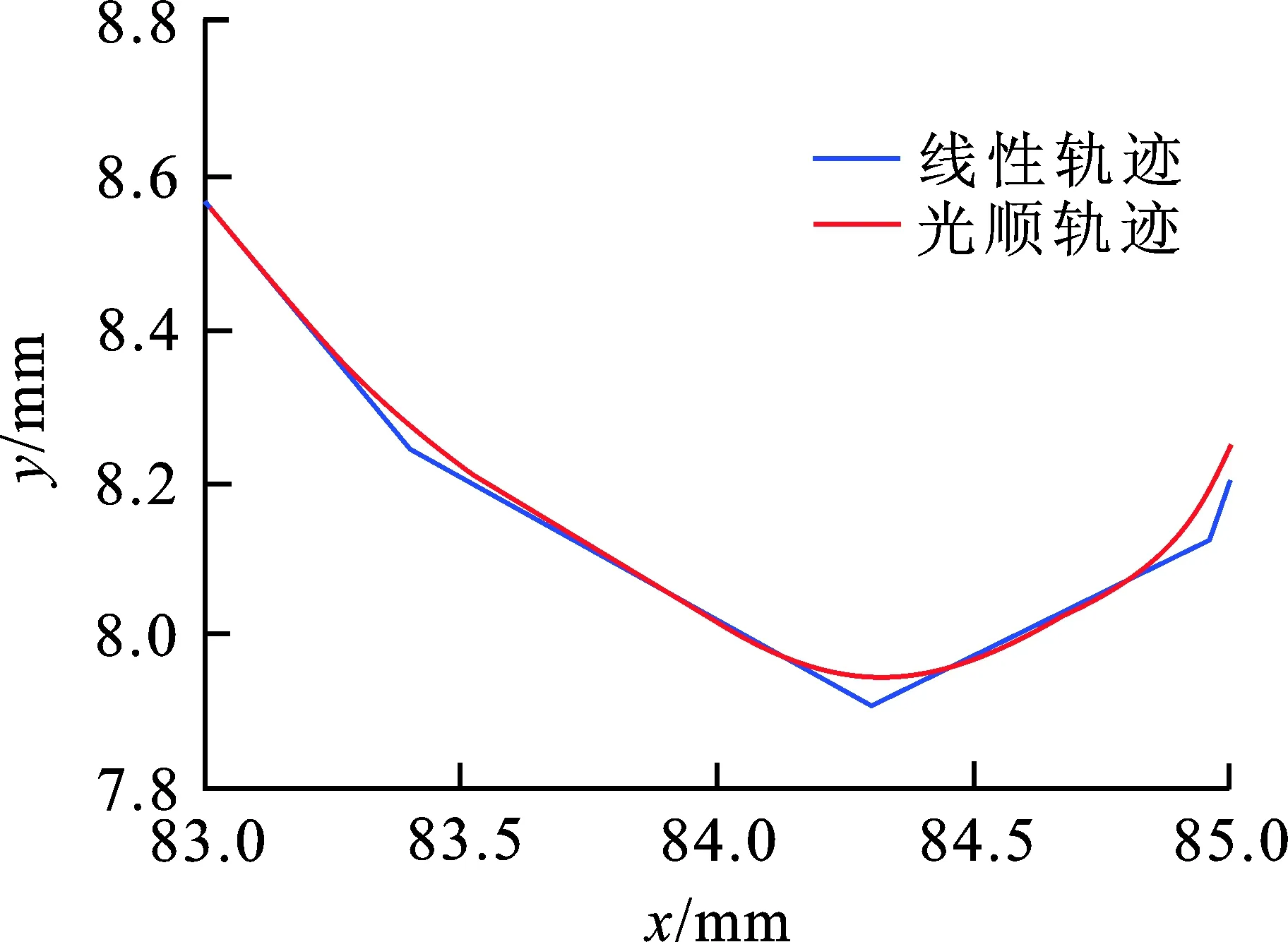
(b) 拐角光顺仿真图 5 混合加工轨迹仿真
图6(a)为混合加工轨迹的轮廓误差分布,其轮廓误差都满足预先设定的约束大小。图6(b)为速度曲线,蓝色实线为未光顺线性加工轨迹速度曲线,红色虚线为混合加工轨迹速度曲线。不难看出混合加工轨迹的速度除了初、末速度为0之外,其余速度均不为0,实现了加工速度非零的效果。与未光顺线性加工轨迹相比较,仿真加工总时间从59.469 s降低到18.631 s,提高了效率。
图7(a)为混合加工轨迹的加速度,虚线为预定最大加速度值,可以看出加速度满足预先设定的约束值。图7(b)为混合加工轨迹跃度,虚线为预定最大跃度值,结果表明跃度满足预先设定的约束值。分别放大两图中部分图像,黑色小方框中的图像表明了光顺曲线处加速度和跃度的连续性。
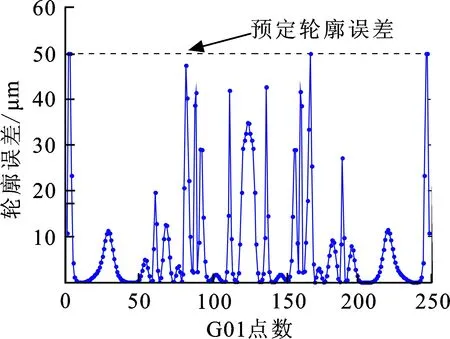
(a) 轮廓误差分布
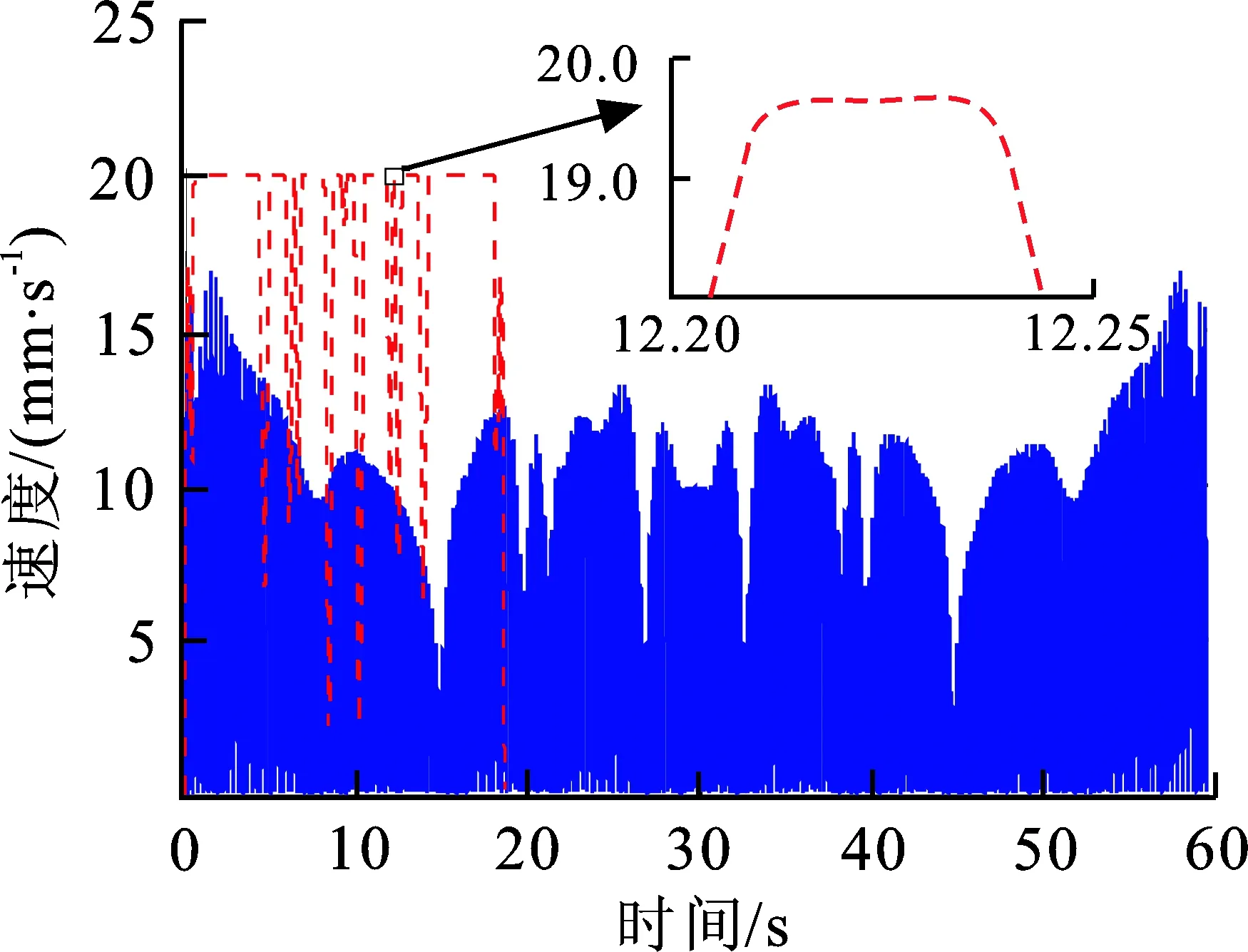
(b) 混合加工轨迹速度曲线
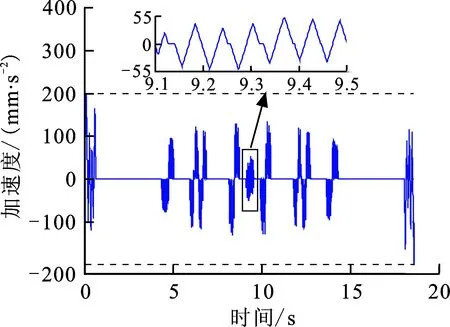
(a) 加速度曲线
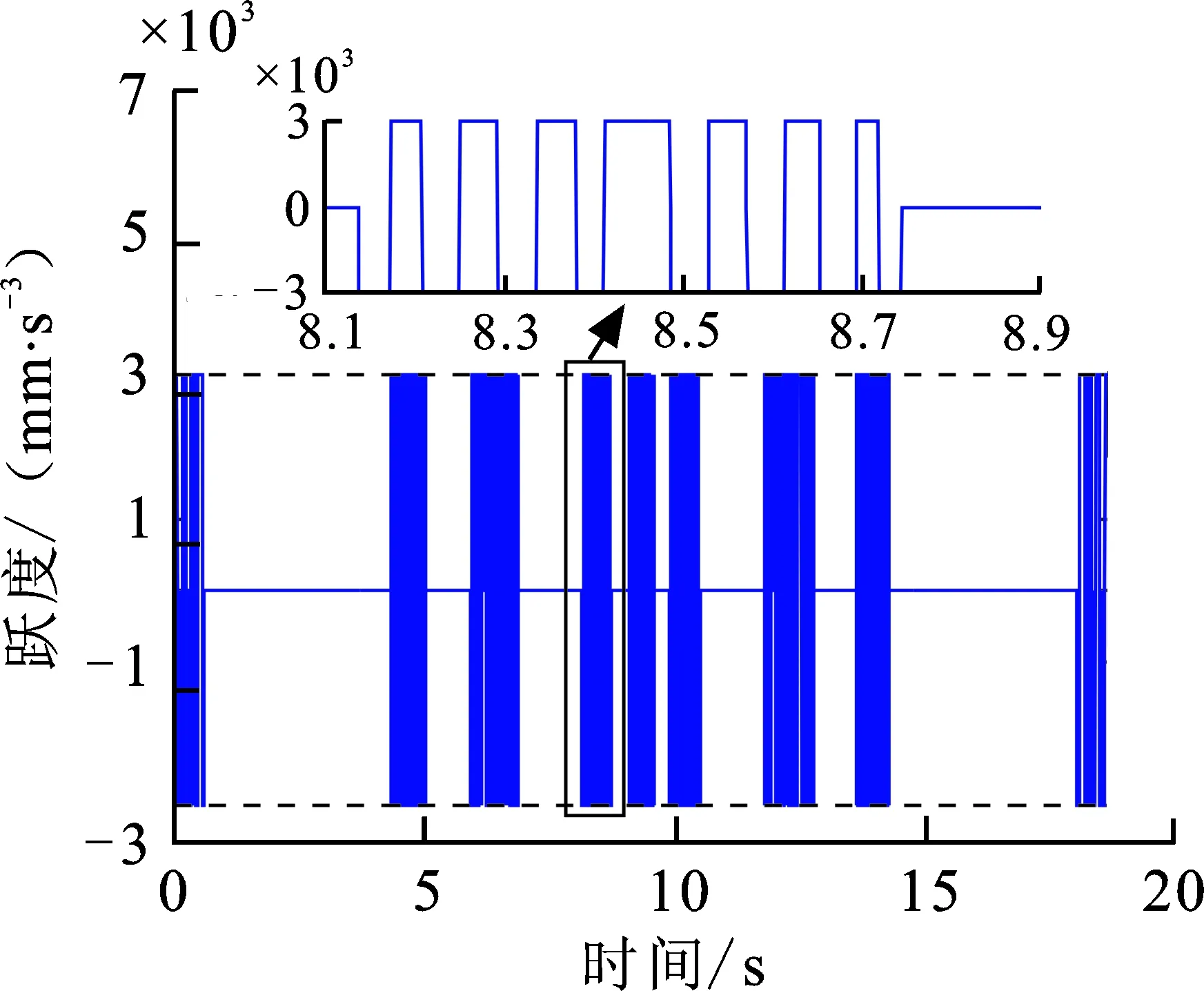
(b) 跃度曲线
在运动控制环节,计算机会将混合轨迹插补后所生成的位置指令传送到运动控制器中以便于反馈控制。图8(a)为插补仿真结果,将红色小方框中图像放大可以看到蓝色粗实线为线性轨迹,红色细实线为羊角光顺轨迹,黑色叉点为插补点的分布。图8(b)中,红色细实线为x位置指令,蓝色粗实线为y位置指令。实验结果表明,本文提出的光顺算法能够有效实现连续微小线性加工轨迹的G2连续光顺,实现了加工速度连续且非零的效果,从而可提高加工效率。
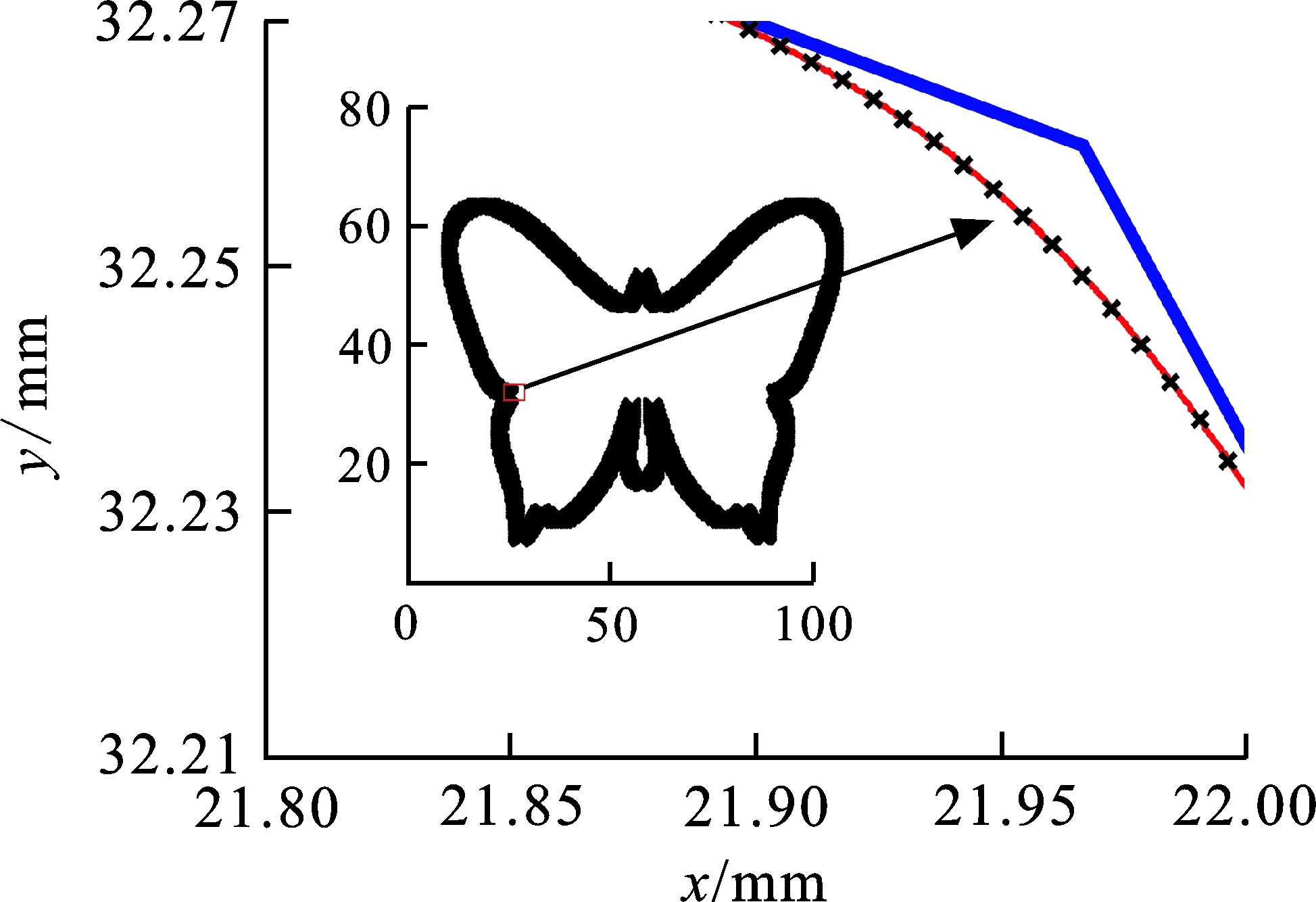
(a) 插补点分布
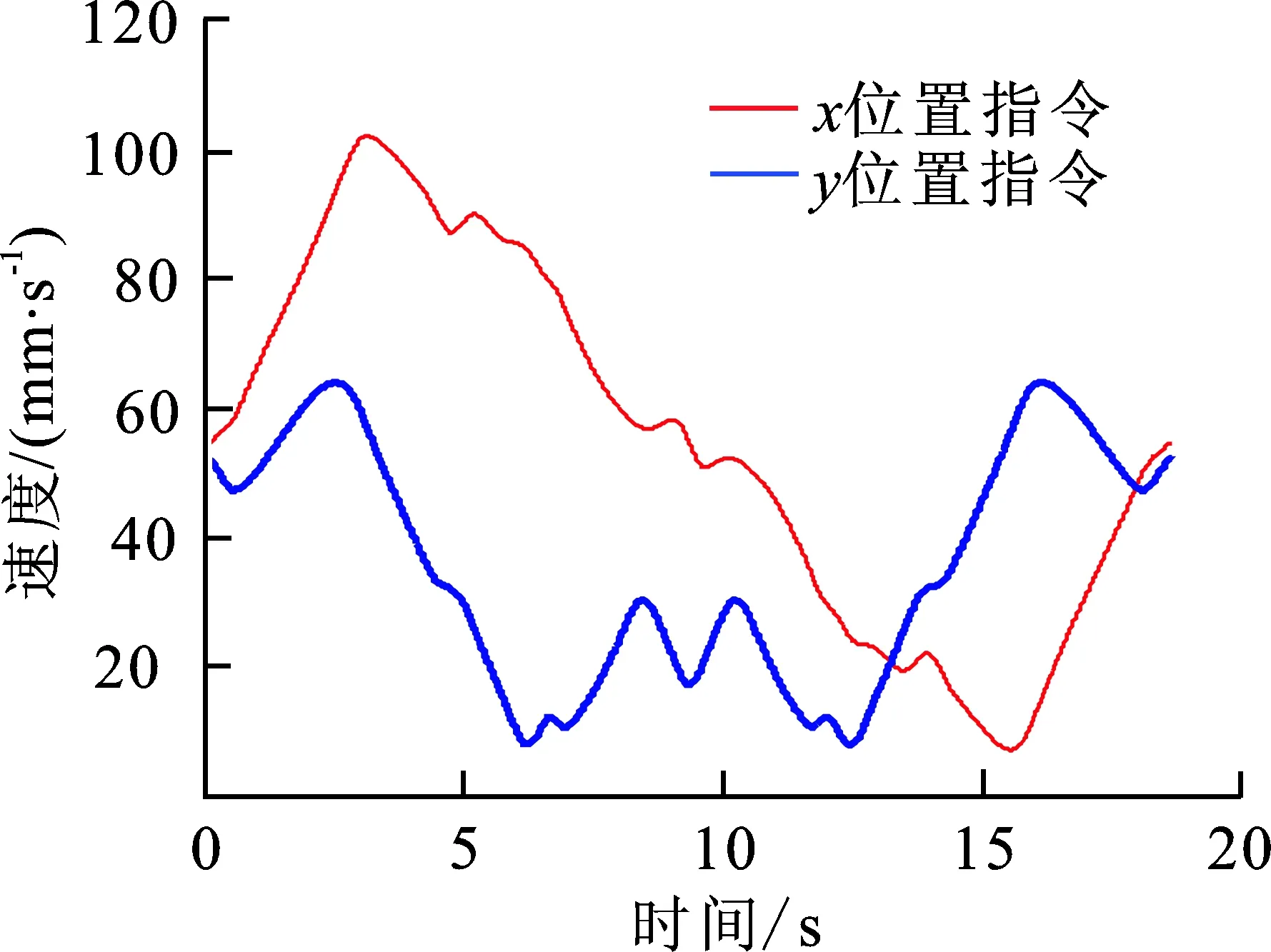
(b) 位置指令
4 结 语
利用羊角曲线过渡线性加工轨迹连接处所产生的拐角,该方法采用双向看策略确定速度规划,再利用插补算法求出混合加工轨迹的插补点。通过MATLAB对算法仿真分析,结果表明该方法能够实现加工轨迹的G2连续、轮廓误差可控和光顺速度非零的效果。
