Optimal control of a mobile robot on sphere

Huageng Liu, Donghua Shi*

School of Mathematics and Statistics, Beijing Institute of Technology, Beijing 100081, China

Keywords:Hamel's formalism Optimal control Pontryagin maximum principle Mobile robot

ABSTRACT For the purpose of solving optimal control problem of a wall-crawling mobile robot working on spherical containers, we propose the Hamel's formalism for Pontryagin Maximum Principle,which gives a general framework for the optimal control of a mechanical system with velocity constraints, especially nonholonomic constraints. The effectiveness of the proposed framework is shown by the simulations for the above problem.

Mobile robots are being widely applied for complex industrial tasks, including the inspections and maintenance of oil tanks,power plant components, etc. The cost associated to the manual inspection is in the order of tens of thousands of dollars for each operation, especially for spherical bodies [1]. In order to seek cost reduction and improvement of procedure's safety in this operation, researches on path planning of mobile robot on sphere have been carried out. Kim and Lee [2] analyzed the movement of mobile robots on three-dimensional smooth surfaces from kinematical viewpoint. Okamoto et al. [1] and Fei et al. [3]modeled this problem from engineering perspectives. However,few of them studied the problem from a dynamical viewpoint and the corresponding optimal control problem has not been addressed sufficiently. In this paper, a dynamical model of a mobile robot working on sphere as well as its optimal control strategy are presented.

The mobile robot working on sphere is subjected to position constraints and velocity constraints, which results in holonomic constraints and nonholonomic constraints, respectively. In general, if appropriate methods are not applied, these constraints will lead to systems of differential-algebraic equations (DAE)and mixed-type differential equations (MTDE), which are known to be difficult to solve numerically. Furthermore, the non-Euclidean configuration space produces high computational complexity in the optimal control problem.

Hamel's formalism features the simplicity of analytic representation of constraints and the intrinsic absence of Lagrange multipliers in the equations of motion. It is exceptionally effective for studying constrained mechanical systems and understanding their dynamics, both analytically and numerically [4] .To handle the computational complexity in optimal control,Hamel's formalism for pontryagin maximum principle is proposed in this paper, which benefits the computation of the optimal problem to avoid solving difficult DAEs and MTDEs.

The paper is organized as follows. First, the Lagrange-d'Alembert principle in Hamel's formalism is briefly discussed.Then, Hamel's formalism for pontryagin maximum principle, a framework for the optimal control of a system with velocity constraints, is derived. Finally, the proposed framework is applied to the optimal control of a mobile robot on sphere.

Let Q be a n-dimensional smooth manifold modeled on a vector space W. A Lagrangian mechanical system is specified by Q and a function L:TQ→ℝ called the Lagrangian, whereTQ is the tangent bundle of configuration space Q. The dynamics of the system is given by the well-known Euler-Lagrange equations [5]. When the velocity components are measured against a proper frame that is unrelated to the system's local configuration coordinates, the Lagrangian and the Euler-Lagrange equations may have a simpler structure, which leads to the Hamel equations [4].

Let V be a neighborhood of q∈Q. Define a family of invertible linear operators {Ψq}q∈Vfrom the model space of Q toTqQ smoothly dependent on q∈Q . Thus, each ξ∈W defines the(local) vector field

For the simplicity of symbols, variables are shown in bold only when they are expressed in terms of components in this paper.

Given two vectorsξ，η∈ W, define an antisymmetric bilinear operation [·，·]q:W × W → W by

where [·，·] is the Jacobi-Lie bracket of two vector fields on the manifold Q.

The dual of [·，·]qis the operation [·，·]q*:W × W*→ W*given by

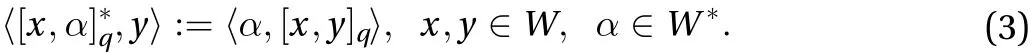
When the mechanical system is equipped with a constraint distribution D, i.e., locally splitting subbundle ofTQ, there exist operators Ψqon V and two closed subspacesWD，WU⊂ W such that W=WD⊕WUand Ψq= ΨqD⊕ΨqU, wheremaps from WDto Dqandmaps from WUto the complementary space ofin[6]. Eachis then uniquely decomposed as

Using the decomposition Eq. (5), the constraints read

Similarly, eachδq∈ TqQ determines uniquely a η by δq= Ψqη Then we have

andη= ηD, or ηU=0.

Given nonconservative forces F∈Γ(T*Q), all sections of T*Q , along the constraint distribution D, the virtual work becomes

Thus, in Hamel's setting, a mechanical system subject to nonholonomic constraints D and external forcesFcould be written as (l，D，f), for which we have thefollowing Lagrange-d'Alembert principle, see Ref. [4]for details.

Theorem 1 (Lagrange-d'Alembert principle in Hamel's formalism). The following statements are equivalent:

① The curve (q(t)，ξ(t)), where a≤t≤b , is determined by the variation principle

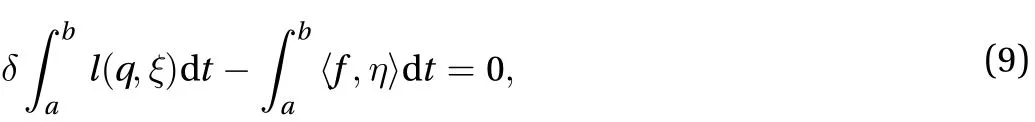
where we choosevariations δq(t) such thatδq(a)= δq(b)=0 and δq(t)∈ Dq(t)for eacht∈ [a，b], and the variations δξ is given by

② The curve (q(t)，ξ(t)) satisfies

coupled with Eq. (5) and Eq. (6), where (·)Dis the projection from TqQ to Dq.

In Theorem 1, q can be reconstructed from ξ by solving Eqs.(5) and (6).

Given a control forceu:[0，tf]→ U (bounded subset of(WD)*), we consider a nondegenerate system (l，D，u). That is,the first-order ordinary differential equations (ODEs) Eq. (10)could be written as=Yu(ξ，q), where Yuis the corresponding vector field of Eq. (10). Then the first-order ODEs Eqs. (5) and(10) with respect to q and ξ could be written explicitly as=Xu(m(t))coupled with Eq. (6), where m=(q，ξD) is an element of M=Q×WD, and Xu(m)=(Ψqξ，Yu(ξ，q)) is the vector field defined by Eqs. (5) and (10) on M.

Given initial point m0and final point m1in the configuration space M, if we require the system (l，D，u) to be optimal according to a certain criterion in the process from m0to m1, the following optimal control problem is proposed

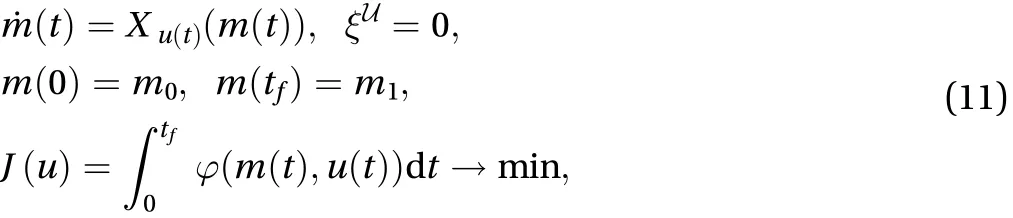
whereφ is a differentiable function on M×U.

In practice, solving Eq. (11) is difficult since the vector field Xuis complicated and the configuration space of the system is non-Euclidean. We propose the following theorem to handle these issues.

Theorem 2 (Hamel's formalism for pontryagin maximum principle). Let U be an open and bounded subset of (WD)*and u be a differentiable curve in U. Define the Hamiltonian

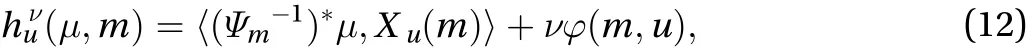
where μ(t)∈ W*×(WD)*is the multiplier of, and ν∈ℝ is a constant, see Ref. [7] for details. The following equations are necessary conditions for Eq. (11)

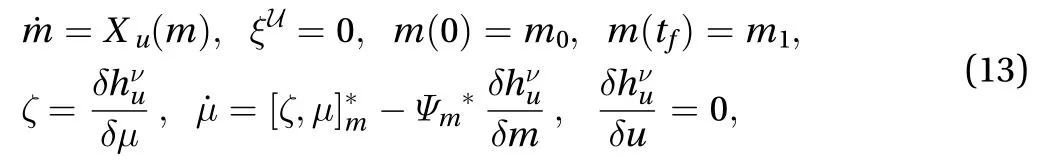
Proof Define a Lagrangian L:TM×WU→ℝ by

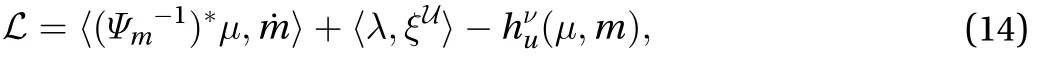
where λ(t)∈ (WU)*is the multiplier of.

By choosing appropriate framein Theorem 2, one could perform symmetry reduction in Pontryagin maximum principle,and avoid using Lagrange multipliers to handle nonholonomic constraints. Consequently, the computational complexity of the optimal control problem (Eq. (11)) is significantly reduced,which will be further illustrated by the optimal control problem of minimizing energy consumption for a mobile robot given initial and final positions on sphere.

A wall-crawling mobile robot consists of two front wheels with fixed directions, a board and a caster (Fig. 1). Two front wheels output different angular velocities, denoted asand.represents the width of the robot,represents the radius of the driving wheels andmeasures the distance between center of mass and contact point, see Ref. [9] for details. Magnetic forces are imposed on the wheels to keep the robot on sphere,which allows one to neglect the gravity. Frictions are also ignored for simplicity. While moving, the robot remains on sphere without slipping. Thus, the robot is subject to both holonomic and nonholonomic constraints.

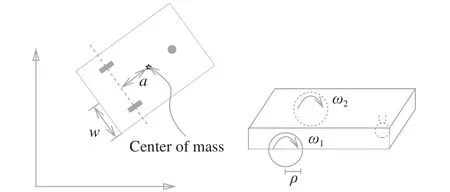
Fig. 1.Two wheeled wall-crawling mobile robots.

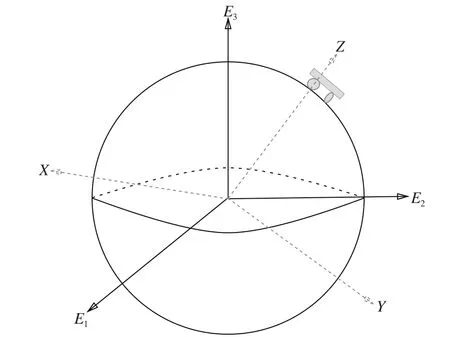
Fig. 2.Mobile robot on sphere.

Body frame of the mobile robot {X ，Y，Z} is selected in the following way:-axis passes through the contact point of the mobile robot and-axis parallels to the heading direction (Fig.2). Consider the initial body frame {E1，E2，E3} as reference frame. Then position and attitude of the mobile robot are described by a rotation matrix R∈SO(3). The body-fixed angular velocity is denoted by:=∈so(3), where ^· is the hat map [5]. The states of the mobile robot are determined by three variableswhich characterize position and attitude of the mobile robot, and rotation degrees of two front wheels, respectively. Thus the configuration space is

Define the invertible linear operatorsfromtoby

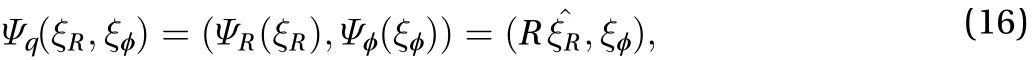
where ξR∈ ℝ3≈ so(3), ξ∈ℝ2and. Thus,andcan be determined uniquely by

The Lagrangian of the mobile robot expressed in body frame reads

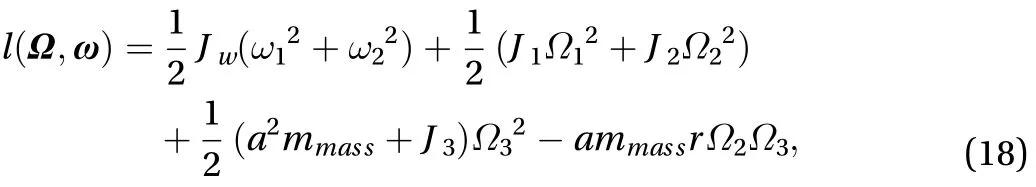
The linear velocity and the angular velocity of the mobile robot are described by the angular velocity of the wheels, i.e.,andare determined byand, which are holonomic constraints. Restrictions on the direction of the front wheels will result in a nonholonomic constraint on[9]. Thus, constraints of the mobile robot are

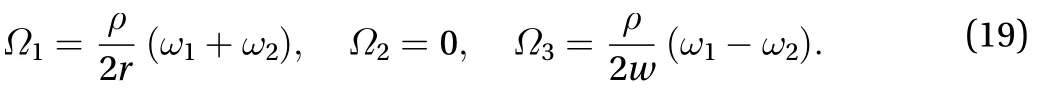
Using Theorem 1 with controlsposed along the directions ofand, we obtain

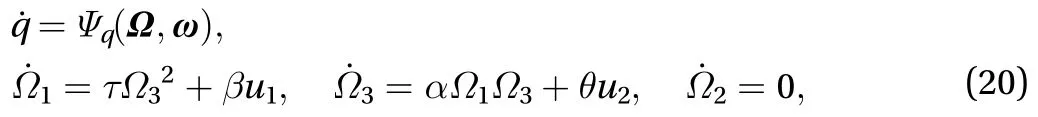
For the inspection task, given initial and final statuses of the mobile robot, the following optimal control problem is proposed.

① Cost functional (minimum energy consumption):

② Boundary conditions:

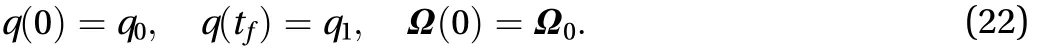
③ Control system is given by Eq. (19).

Let M=Q ×ℝ3=SO(3)×S1×S1×ℝ3andDefine the invertible linear operatorfromtoby

Using Theorem 2, the following control laws are obtained:

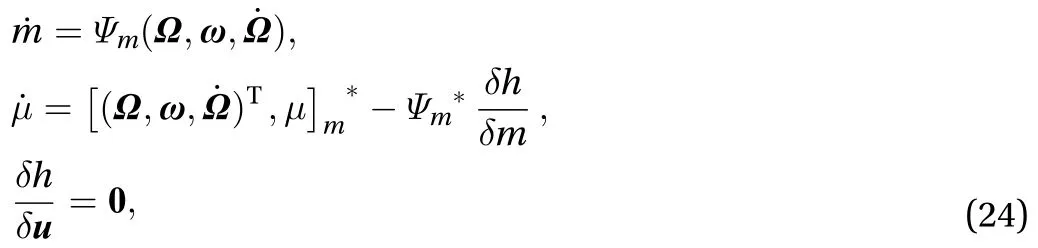
coupled with boundary conditions Eq. (22), which is a two-point boundary-value problem without algebraic equations. Accordingly, it could be solved by the standard shooting method with the optimization toolbox of Matlab.

For simulation, we specify three sets of open-loop control and compare their energy consumption (EC) with the one of the corresponding optimal control under the same boundary conditions. Letdenote the open-loop control. Select the parameters and the boundary conditions of the system to be

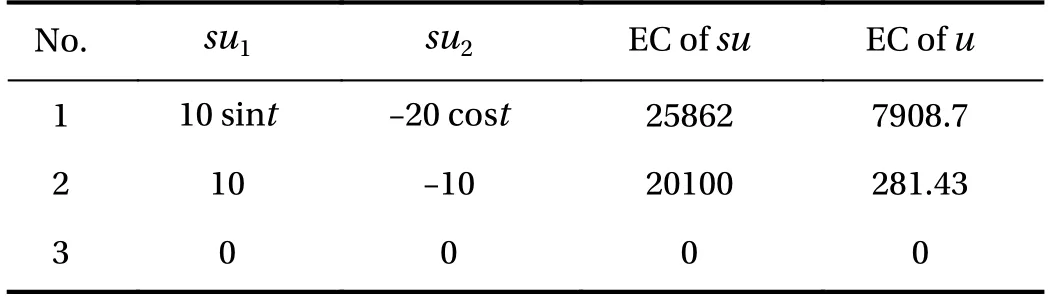
Table 1EC of su and u in three sets of comparison.

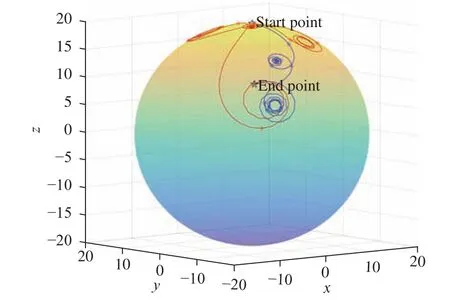
Fig. 3.Trajectories of open-loop control and optimal control in the first set of comparisons, indicated in red and blue respectively.

Fig. 4.Controls of open-loop control and optimal control in the first set of comparisons.

From the simulation results in Table 1, we conclude that the control given by Theorem 2 is more energy-efficient than the open-loop control.

The trajectories of open-loop control and optimal control in the first set of comparisons, indicated in red and blue respectively, are shown in Fig. 3. Figure 4 shows the controls,and,throughout the process. Figure 5 demonstrates the orthogonal-

Fig. 5.Orthogonality of R∈SO(3).

In conclusion, we proposed the Hamel's formalism for pontryagin maximum principle and applied it to the optimal control of a mobile robot on sphere. Future work will include the further study of the underlying geometric structure of the optimal control problem, as well as the discrete Hamel's formalism for pontryagin maximum principle.

Acknowledgement

The authors thank the National Natural Science Foundation of China (Grant 11872107) for support, as well as the constructive suggestions from the reviewers.