Dependency of gamma oscillations in E/I neuronal network on illumination contrast of external stimulus

Xiaochun Gu, Fang Han*, Zhijie Wang*, Xia Peng

College of Information Science and Technology, Donghua University, Shanghai 201620, China

Keywords:Gamma oscillations Illumination contrast E/I network Receptive field

ABSTRACT Synchronous gamma oscillations are believed to play a prominent role in the information processing of biological neural systems. Experimental observations have found that the frequency and power of gamma oscillations in the primary visual cortex (V1 zone) are regulated by the illumination contrast of visual stimulus. However, the underlying mechanism of how the synchronous oscillations depend on the illumination contrast has not been well explained. We propose a local excitatory/inhibitory (E/I) neuronal network of integrate-and-fire (IAF) neurons with the difference-of-Gaussians (DOG) receptive field to unveil this mechanism. Simulation results demonstrate that the higher the illumination contrast, the higher the frequency of gamma oscillations. The power of gamma oscillations also increases with the increase of illumination contrast. These results are consistent with the experimental findings.

Synchronous oscillations with frequency between 30-90 Hz(gamma oscillations) have been found in various brain regions,which are thought to be the intrinsic foundations of many cognitive functions such as the processing of sensory signals, attention mechanism, learning and memory. Experimental observations have suggested that visual stimulation can cause high-frequency synchronous oscillations in primary visual cortex [1-3].Demiralp et al. [4] found the high-frequency synchronous oscillations with a frequency of about 40 Hz when the subjects identified image stimuli. Joerg et al. [5] found the high-frequency synchronous oscillations with a frequency of 64-128 Hz when the subjects perceived a visual-aural mixed signal. Recent experimental researches have further found that the characteristics of stimulus play an important role in the generation of high-frequency oscillations, for example, different illumination contrast of visual stimulus can cause gamma oscillations in different frequency bands, i.e. the frequency of gamma oscillations caused by different visual stimulus was not fixed [6, 7]. Adjamian et al. [8]found that the high-frequency oscillations in the primary visual cortex (V1 zone) were related to the illumination contrast. Henrie and Shapley [9] found that the high-frequency synchronous oscillations in V1 zone strengthen with the increase of illumination contrast, and the high-contrast visual stimulus can cause high-frequency synchronous oscillations. Perry et al. [10] further found the oscillation frequency would grow linearly as illumination contrast increases.

In order to explain aforementioned experimental observations, it is necessary to establish the relevant models of biological neural networks to regenerate these experimental observations. Most models on gamma oscillations up to date focus on the generation mechanism of oscillations with fixed frequency.The scenario that the oscillation frequency is dependent on the properties of stimulus signals is seldom considered. Some researches [11-13] have studied the regulation of synchronized oscillations with various input signals, but they focused on low-frequency oscillations (alpha oscillations). Jadi and Sejnowski [14,15] constructed an excitatory/inhibitory (E/I) neural network consisting of simple stochastic neurons to explore the dependency of gamma oscillation on the illumination contrast of visual stimulus. Their results showed that the peak frequency of oscillations increased whereas the peak power of oscillations decreased if the illumination contrast to the excitatory neurons increased, and it was in opposite directions when the visual contrast to inhibitory neurons was enhanced.

Up to date, in the modeling studies on the relationship between gamma oscillations and illumination contrast, the actual characteristics of real world stimulus have not been considered. In addition, the adopted neuron models were the simplified ones (for example, simple stochastic neurons were used[14, 15]). Especially, the neuronal characteristic in V1 zone such as the receptive field are not well considered in the current models. Therefore, the modeling researches on the underlying mechanisms of the frequency-dependency of the synchronized gamma oscillations on input signals are far from sufficient.

In this paper, we establish a local excitatory/inhibitory neuronal network composing of integrate-and-fire (IAF) neurons with the difference-of-Gaussians (DOG) receptive field to explore how the synchronous gamma oscillations change with the illumination contrast of the visual stimulus. Simulation results show that the peak frequency and peak power of gamma oscillations generated in this E/I network both increase with the enhancement of illumination contrast, which is consistent with the biological experimental results well.

The neuronal network model consists of excitatory neurons(E neurons) and inhibitory neurons (I neurons) with the DOG receptive field mimicking simple neuronal circuits in V1 zone.Figure 1 shows the structure of the E/I network with all to all connections wherein neurons receive external inputs mapped from an grating stimulus (image) through the receptive fields. In Fig. 1, only three cells of E population (red dots) and I population (blue dots) are depicted. Each excitatory (inhibitory) neuron connects to all inhibitory (excitatory) neurons. wEE, wII, wEI,and wIEare the synaptic weights of E to E, I to I, E to I, and I to E connection, respectively. Schematic on the left in Fig. 1 is the spatial structures of the receptive fields of E neurons (lower) and I neurons (upper) respectively. The receptive field superimposing on grating stimulus (top right) is shown as two oval regions,the dark one to represent an OFF area and the white one to denote an ON region.

IAF model neurons and conductance-based synapse model[16] are used to construct the E/I neuronal network. The network is described by

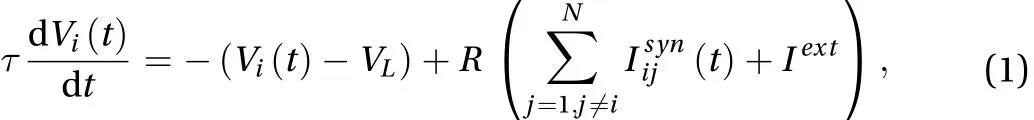
where Vi(t) denotes the membrane potential of neuron i at time t,is the membrane time constant, R is the membrane resistance, VLis the equilibrium potential of leakage ions,denotes the synaptic current transmitted from neuron j to neuron i at time t, N denotes the number of the neurons in the network,is the external input of neuron i.

Assume that the step length is Δt, Eq. (1) can be rewritten as

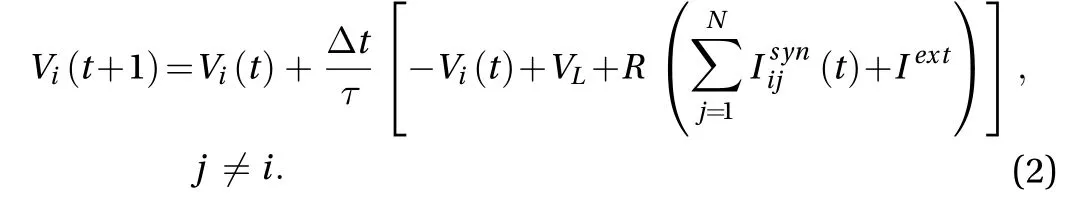
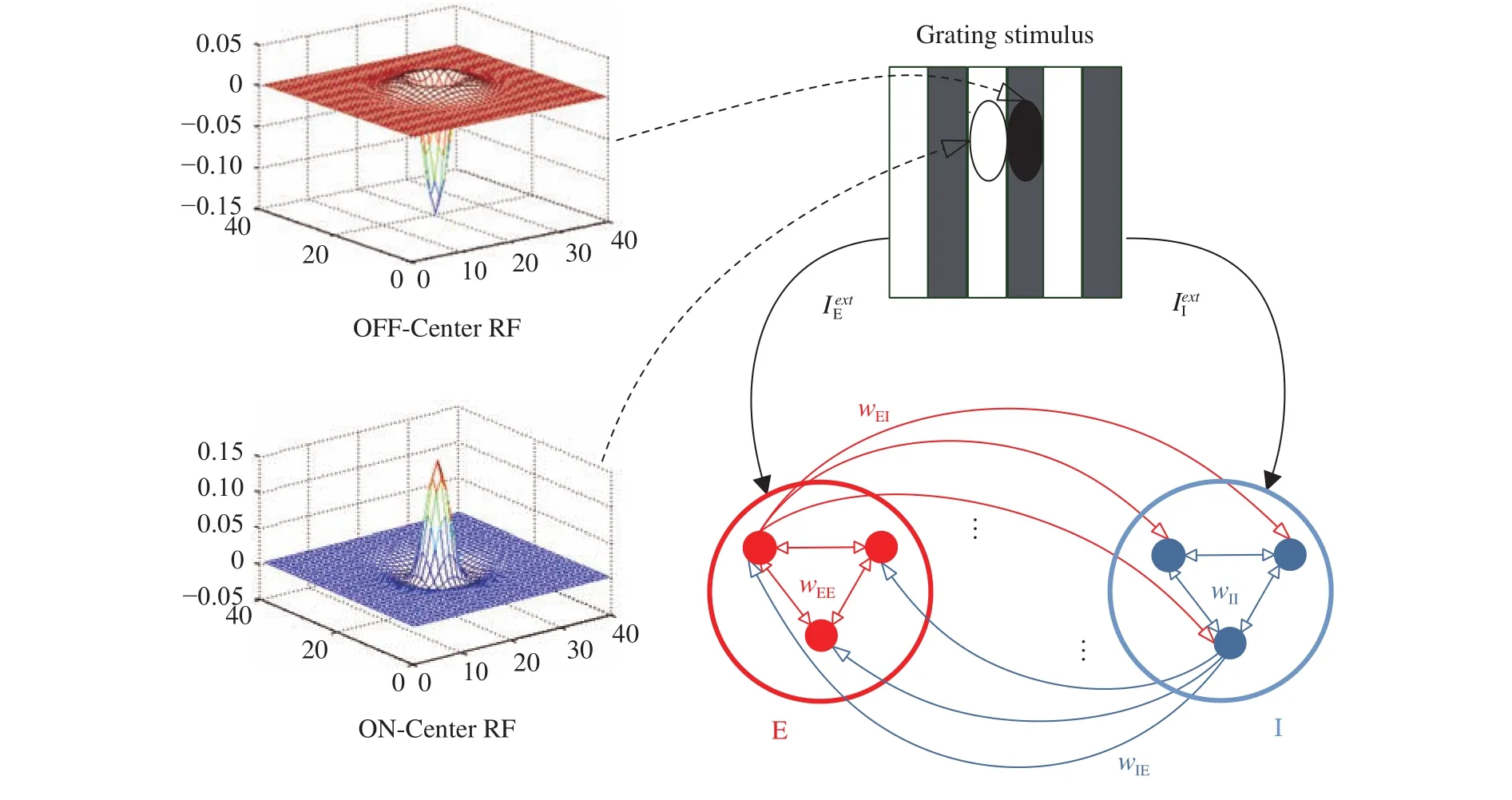
Fig. 1.Architecture of the E/I neuronal network.

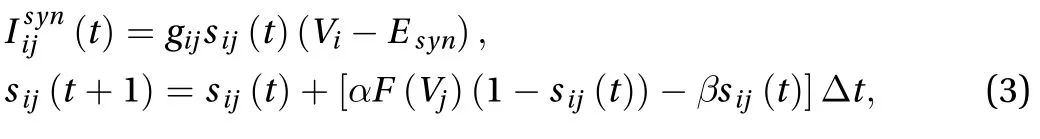
where sij(t) denotes the level of the opening of the synaptic ion channel from neuron j to neuron i, gijis the maximum synapse conductance of the synapse (the synaptic weight), and Esyndenotes the reverse potential of synapse.is the gate enhancement factor,is the gate decay factor, Vjis the membrane potential of neuron j. After neuron j is discharged,the resulting action potential reaches the synapse after a certain time (synaptic delay) and then F (Vj) = 1, otherwise F (Vj) = 0.

Excitatory and inhibitory neurons in the network model are both IAF neurons but their parameters are different. The time constant τ of I neurons is less than that of E neurons to ensure the faster spiking of I neurons (see Table 1 for details). Table 1 shows the parameter settings of the network where Vthis the spiking threshold potential, Vrestis the resting membrane potential, w is the connection weight between neuronal synapses,delay time is the synaptic delay time of the network.

Neurons in primary visual cortex respond to various stimulations in restricted regions of the visual field called receptive fields (RF) [17]. Receptive fields are classified into two styles according to the location of the excitatory region and the inhibitory region, called ON-Center and OFF-Center respectively [18, 19].The ON-Center RF is a circular central excitatory region surrounded by an annular inhibitory region. In contrast, the OFFCenter RF has the opposite arrangement of a central inhibitory region surrounded by an annular excitatory region.

Gaussian models can generally be used to imitate the receptive field of neurons in the visual areas. DOG model for the classical receptive fields proposed by Rodieck [20, 21] provides a closer match to the cells for processing low-level visual information. Therefore, we use DOG model to set up the spatial structure of the receptive field of neurons in this paper (see Fig. 1).DOG model is formed through mutual antagonism between a stronger excitatory central mechanism and a weaker but larger region of inhibitory surrounding mechanism [16]. Its spatial structure function is expressed as

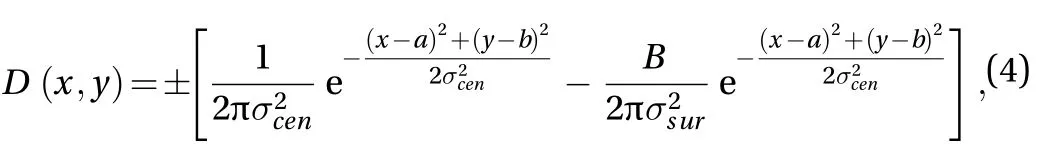
where the center of the receptive field is placed at the point (a,b).determines the size of the central region.determines the size of the surround region, which is greater than. B controls the balance between center and surround contributions. The ± sign denotes ON-Center case (corresponding to E neurons) and OFF-Center case (corresponding to I neurons),respectively.

We assume that E neurons are sensitive to the light stripes of grating stimulus and I neurons are sensitive to the dark stripes of grating stimulus. Thus, light bands are arranged to overlap the ON area of the receptive field of E neurons and dark bands are arranged to overlap the OFF areas of the receptive field of I neurons (see Fig. 1).

Synchronous gamma oscillations can be formed by the interaction of both E and I neurons in the network, which is called PING mechanism, or by the I neurons solely, which called ING mechanism [22, 23]. In this paper, synchronous gamma oscillations are driven by the interaction of E and I neurons in the E/I neuronal network following PING mechanism. External inputs have also impact on the genesis of the gamma oscillations, i.e.,gamma oscillations in E/I network is caused by the integrated effects of synaptic currents from E and I neurons and external stimulus inputs. Importantly, some evidences show that inhibitory fast-spiking neurons are essential to the generation of gamma oscillations [24]. Additionally, in the cortical region of V1 where gamma oscillations are observed, there are actually many fast spiking neurons. Therefore, we assume that the time constantof I neurons in the network is smaller than E neurons in order to make I neurons discharge more quickly under the same stimulus input. We propose the method of using the power spectrum of the average population activity and the grating image with different illumination contrast to explore the gamma oscillations, then discuss the dependency of the gamma oscillations on the illumination contrast later.

Difference in gray-scale values between light stripes and dark stripes of grating stimulus is assumed to mimic the illumination contrast of the external visual stimulus to the E/I network. Let the gray-scale value of light stripes corresponding to E neurons denoted by G1 and the gray-scale value of dark stripes corresponding to I neurons denoted by G2, the illumination contrast ΔG is defined as

where Gmaxis set to 255 (the maximum gray value of a pixel coded by a byte) in this paper. Thereby, we can change the illumination contrast ΔG by changing the gray-scale values G1 and G2 to observe the variation of the frequency and power of gamma oscillations in the E/I network.

For each neuron i in the E/I network,(the external input of neuron i in response to illumination contrast of a grating image) is mapped from the image through the receptive field as

where G is the grating stimulus (image) and its size is m×n (m =200 and n = 200 in this paper), G(x, y) is the gray-scale value at (x,y). Diis the spatial structure of the receptive field of neurons.Since each neuron of the E/I network has a receptive field withthe fixed structure, the external inputto E and I neurons are mainly determined by the gray-scale values of light stripes and dark stripes (denoted by G1 and G2, respectively). The receptive field parameters in Eq. (4) for E neurons are= 0.8,= 1.5,B = 0.1 and for I neurons are= 0.55,= 1.5, B = 0.15.

Table 1Parameters in the model.

We simulated 400 excitatory neurons and 100 inhibitory neurons with all-to-all connections. The network model is simulated in MATLAB 2012a with a clock-driven algorithm [25]. The biological time of this E/I network is one second. Firstly, we tune the network in the case that there is no external input to E and I neurons (i.e.= 0) and no illumination contrast (ΔG = 0) to the E/I network. By adjusting cell parameters to the values listed in Table 1 to make the network be in a balance of excitatory and inhibitory synaptic currents, irregular spiking activities emerge(Fig. 2(a)). Figure 2(b) is the average population activity which is calculated from Fig. 2(a) by counting spikes in time bins of width 1 ms and convolving with a Gaussian of width 100 ms [6]. The power spectrum of the average population activity in Fig. 2(c) is calculated using the method of fast Fourier transformation (FFT)transform. The peak in the power spectrum is the frequency component that has the largest power, and the frequency at this peak is the oscillation frequency. As shown in Fig. 2(c), there is no evident peak in the power spectrum, indicating that there is no obvious oscillation in the network with no illumination contrast. We will regulate the network based on the above balanced network by increasing the contrast ΔG (i.e., increasing the difference between G1 and G2) later. It is worthy of noting that the frequency of gamma oscillations is usually above 25 Hz and below 100 Hz, therefore we draw the power spectrum with frequency between 25 Hz and 100 Hz in the following figures.

We regulate the gamma oscillations and observe the variations in frequency and power of the oscillations by increasing the illumination contrast ΔG from 0 to a large value in the following two scenarios: ① reduce the gray-scale value of dark stripes G2 and keep the gray-scale value of light stripes G1 unchanged； ② increase the gray-scale value of light stripes G1 and reduce the gray-scale value of dark stripes G2 simultaneously.The larger the difference between G1 and G2 of grating stimulus is, the higher the illumination contrast is.

Firstly, we simulated our network in the first scenario under a typical illumination contrast that reduces G2 by 40% but keeps G1 unchanged (the initial values of both G1 and G2 are 255).Thereby, the illumination contrast ΔG is increased by 40%. Similar to the data analysis in Fig. 2, we plotted separately the spiking times of neurons, the population spiking activity and the power spectrum in Fig. 3. We can visually observe from Fig. 3(a)that the raster plot is periodic (in contrast, the raster plot in Fig. 2(a) has no obvious periodicity.). We can get by counting 20 cycles between 50 ms and 450 ms, i.e. 50 cycles in 1 s, which is the frequency corresponding to the peak point in Fig. 3(c) (about 50 Hz). In Fig. 3(b), we can also get by counting about 50 cycles between 50 ms and 450 ms, i.e. about 50 cycles in 1 s, which also coincides with the frequency corresponding to the peak point in Fig. 3(c) (about 50 Hz). The peak power of the frequency component near 50 Hz in Fig. 3(c) is about 1600 which is much larger than those of other frequency components, implying that gamma oscillation is quite strong while feeding the visual stimulus with medium illumination contrast (40%) to the network.

The peak frequency and peak power of gamma oscillations regulated by the illumination contrast in the first scenario with reducing G1 from 255 to 0 gradually and keeping G2 unchanged are summarized in Fig. 4. Figure 4 shows that the peak frequency of the gamma oscillations increases gradually (Fig. 4(a))and the peak power become stronger (Fig. 4(b)) with the increasing of the illumination contrast, which is consistent well with the biological experimental results [9].

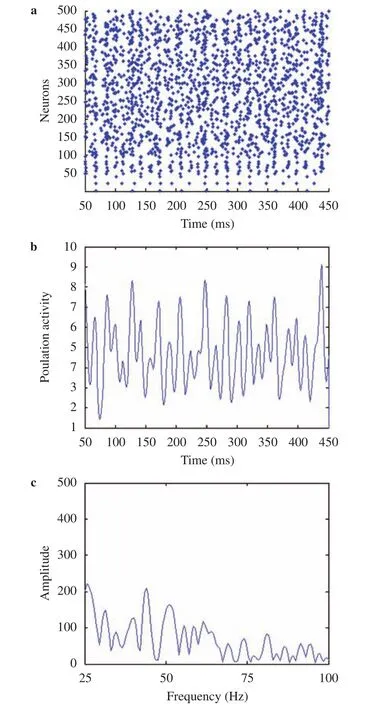
Fig. 2.Simulation results of the E/I network with no illumination contrast ΔG = 0 (G1 = 0 and G2 = 0). The data shown are for 50-450 ms of a simulation. a Raster plots of the spiking times of neurons.Neurons indexed 1-100 are inhibitory neurons and neurons indexed 101-500 represent the excitatory neurons. b Average population activity. c Power spectrum of the average population activity.

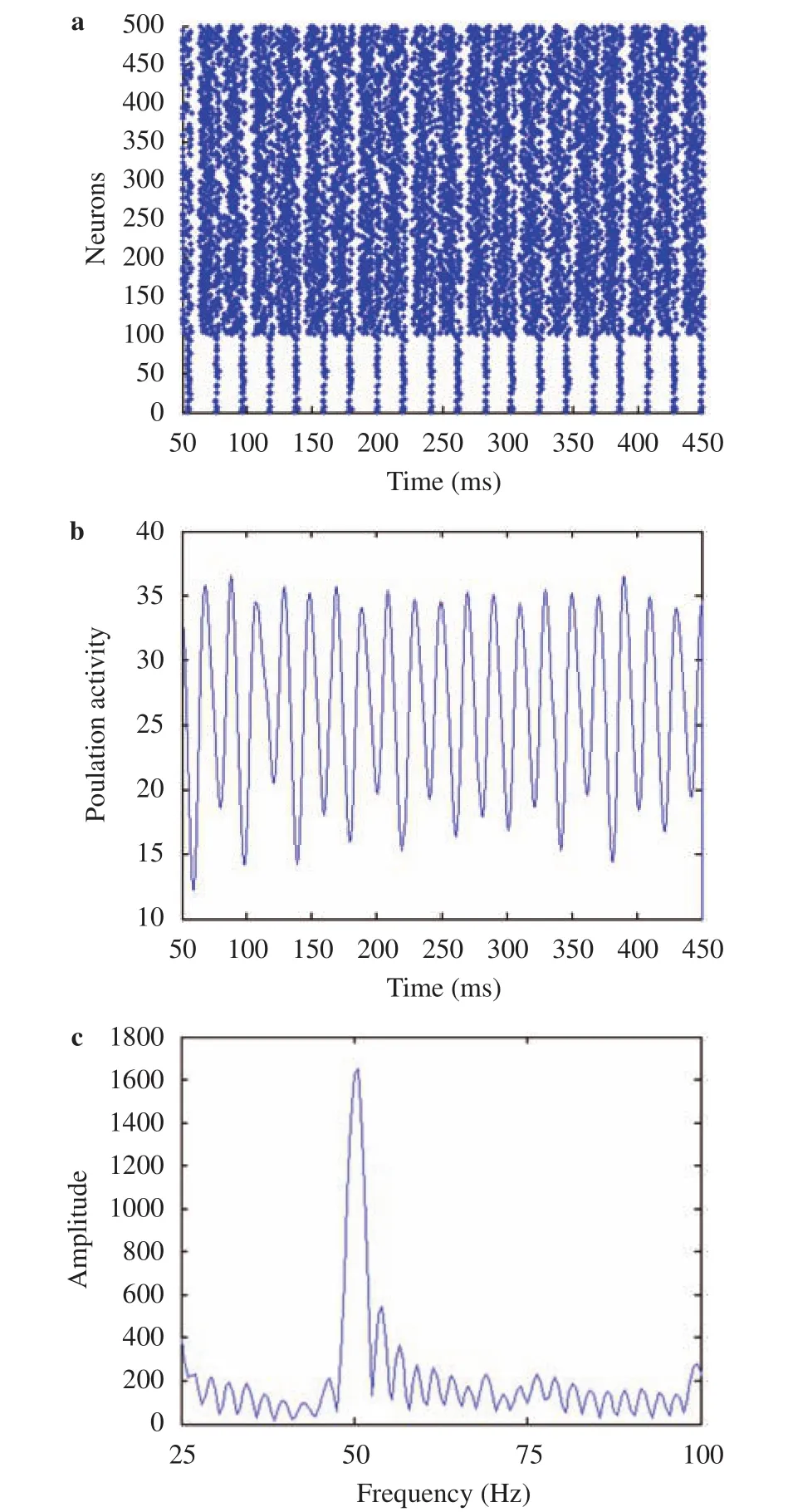
Fig. 3.Gamma oscillations generated by a typical illumination contrast for the first scenario (40% increase in illumination contrast by reducing the gray-scale value of dark stripes G2 by 40%). a Raster plots of the spiking times of neurons. b Average population activity.c Power spectrum of the population activity.

We also simulated the network in the second scenario under a typical illumination contrast that increases G1 by 30% and reduces G2 by 30% simultaneously (the initial values of both G1 and G2 are 127). Thereby, the illumination contrast ΔG is increased by 60%. The result under this typical illumination contrast in Fig. 5 is similar to that in Fig. 3, meaning that the gamma oscillations can be induced with the illumination contrast of external grating stimulus in the second scenario. The dependency of the peak frequency and peak power of gamma oscillations on the increasing of the illumination contrast in the second scenario with increasing G1 from 127 to 255 and reducing G2 from 127 to 0 simultaneously are summarized in Fig. 6, indicating that the oscillation frequency (peak frequency) becomes faster and oscillation also gets stronger (i.e., the power of the peak frequency gets stronger).

Fig. 4.Summary of synchronized characteristics of network activity in response to the illumination contrast for the first scenario with reducing G1 from 255 to 0 gradually and keeping G2 unchanged.a Modulation of the peak frequency of gamma oscillations. b Modulation of the peak power of gamma oscillations.

A more steep upward trend in the peak frequency and peak power shown in Fig. 4 compared to that in Fig. 6 indicates that the network is more sensitive to the changes of I neurons in stimulus contrast (note that for the first scenario, G2 is reduced but G1 keeps unchanged implying that the inputs of I neurons are affected notablely but the inputs of E neurons remain approximately unchanged). This is consistent with many evidences that inhibitory neurons may be more important than excitatory neurons for the genesis of the gamma oscillations [26].

In short, both the simulation results in Fig. 4 (with only reducing G2 to increase illumination contrast) and Fig. 6 (with increasing G1 and reducing G2 simultaneously to increase illumination contrast) show that the peak frequency and peak power increase with the increase of illumination contrast of external grating stimulus (image), which is consistent well with the biological experimental results [9, 10].

In order to explain the biological experimental observations that gamma oscillations are regulated by the illumination contrast of the visual stimuli, we construct an E/I neuronal network consisting of IAF neurons with the DOG receptive field to explore the dependency of gamma oscillations on illumination contrast. The illumination contrast is defined by the difference in gray-scale values between light stripes and dark stripes of a real grating image. The inputs of the neurons are mapped from the grating image through their receptive fields. We use the power spectrums of the average population activity of the net-work to analyze the simulation results, which show that the larger the illumination contrast is, the higher the frequency of the gamma oscillations is and the stronger of the gamma oscillations is.

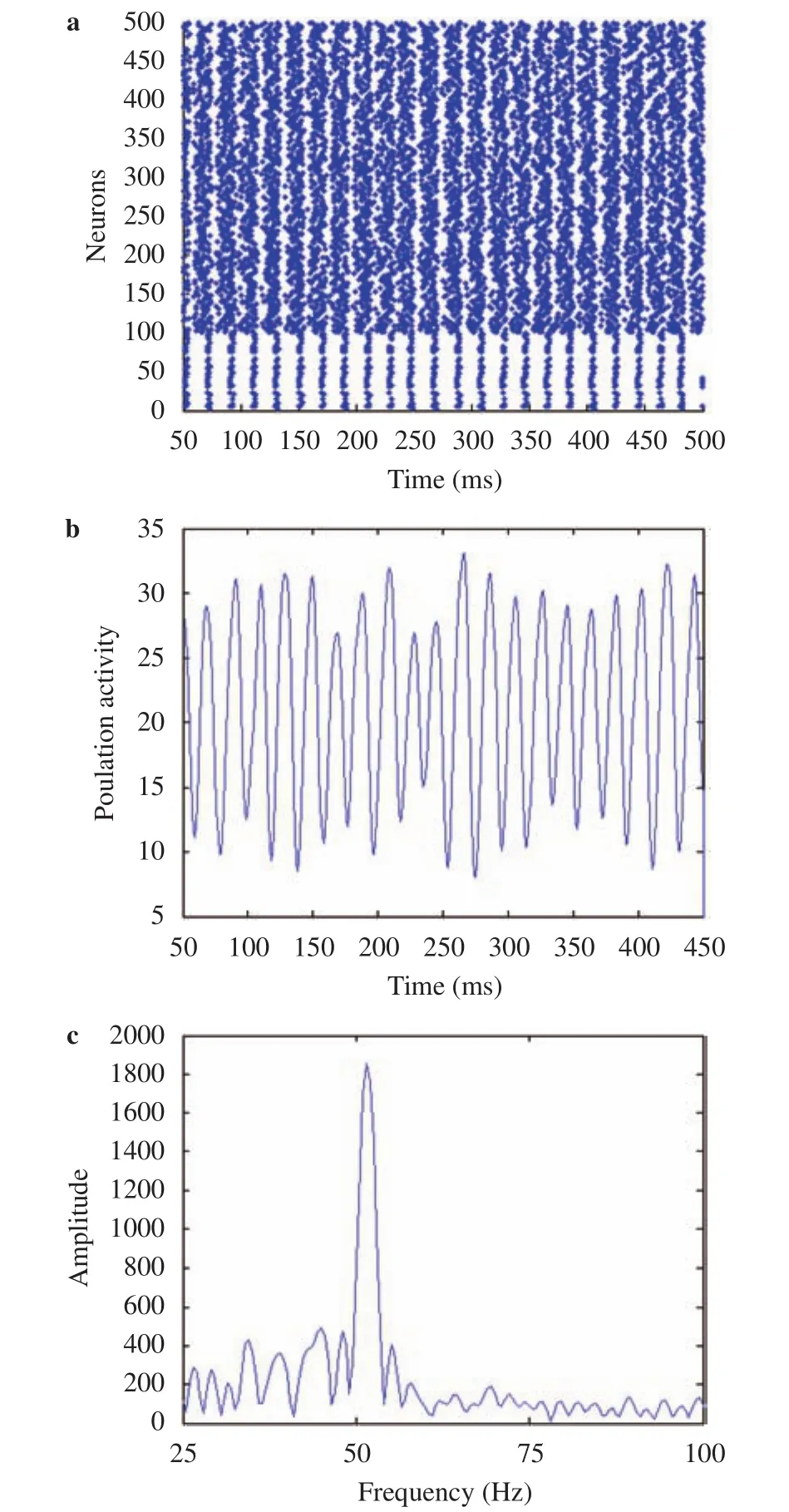
Fig. 5.Gamma oscillations generated by a typical illumination contrast for the second scenario (60% increase in illumination contrast by increasing the gray-scale value of light stripes G1 by 30% and reducing the gray-scale value of dark stripes G2 by 30% simultaneously). a Raster plots of the spiking times of neurons. b Average population activity. c Power spectrum of the population activity.

The results with our models are consistent well with the biological experimental observations that gamma oscillations are regulated by the external stimuli, especially by the illumination contrast [9, 10]. This gives us a possible way to understand the mechanism of the regulation of the gamma oscillations by the external stimuli. It may also be a possible approach to explore the functional role of gamma oscillations in the neural information processing of the external stimuli. In addition, to check whether the results in this paper is valid if other neuronal models such as H-H models are adopted, we have carried out some researches with H-H models. The preliminary results are similar to those in this paper. We will further verify these results with detailed simulations in our future works.

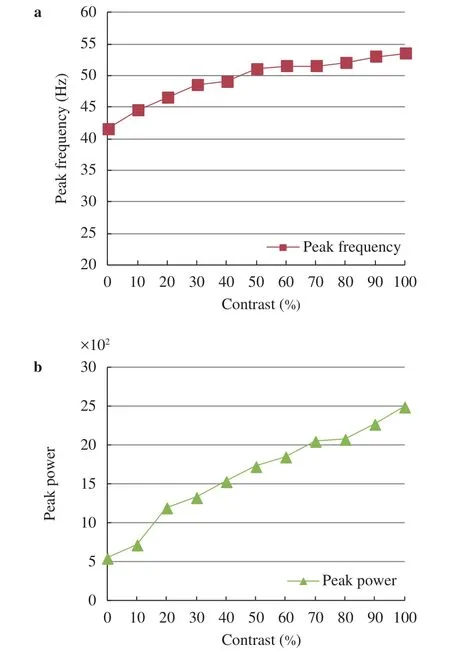
Fig. 6.Summary of synchronized characteristics of network activity in response to the illumination contrast for the second scenario with increasing G1 from 127 to 255 and reducing G2 from 127 to 0 simultaneously. a Modulation of the peak frequency of gamma oscillations. b Modulation of the peak power of gamma oscillations.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grants 11572084, 11472061, and 71371046), the Fundamental Research Funds for the Central Universities, and the DHU Distinguished Young Professor Program (Grant 18D210402).