Seepage-stress coupled modeling for rainfall induced loess landslide
2019-03-07DnyngZhouZhenZhngJichunLiXiolingWng
Dnyng Zhou, Zhen Zhng*, Jichun Li, Xioling Wng
a Key Laboratory for Mechanics in Fluid Solid Coupling Systems, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190,China
b School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China
Keywords:Loess Rain infiltration Seepage-stress coupling Strength weakening Landslide
ABSTRACT Although rainfall is rare on the Loess Plateau of western China, landslides occur frequently there in rainy season. Surveys report that landslide hazards always follow heavy rains. In this study, a seepage-stress coupling model for rainfall induced landslide is used to examine an actual disastrous event in Yulin by the end of July, 2017. The effects of rainfall duration, rainfall intensity and soil weakening on slope stability are studied in detail. The results illustrate that the safety factor drops sharply at first and then is gradually declining to below 1.05 during additional two days of heavy rain. With soil strength softening considered, the slope would be more unstable, in which the weakening in soil cohesion is found to be a more sensitive factor.
Loess, which widely covers western plateau of China, is characteristic of a special macro-pore structure and hydrologic sensitivity [1]. It was reported that one-third of China's landslides happened in loess areas during the period of 2002-2012 [2]. Due to the macro-pore and vertical joint structure of loess, rapid rain infiltration leads to immediate rise of saturation and pore pressure along with drop in soil strength, all of which are mainly responsible for plenty of loess landslides in rainy season. Hence,rainfall turns out a primary trigger for this kind of hazard there[3]. On July 25, 2017, an extremely heavy storm occurred in Yulin city at the north of Shannxi Province. Then loess landslides followed in numerous places, thus resulting in catastrophic disasters. Therefore, the study on loess landslide and seepagestress coupling mechanism can no longer be neglected.
In regard to rain infiltration, a number of scholars have fulfilled extensive studies. Tu et al. [4] carried out artificial rainfall tests on the slope of Loess Plateau, monitoring the variations of water content, matrix suction and pore pressure in the soil during the process. By using kinetic wave theory and improved Green-Ampt model, Chen et al. [5] analyzed water motion in soil and runoff generation over a loess slope in typical erosion areas.Mein et al. [6] and Chu [7] modeled steady and unsteady infiltration with experimental verification, respectively. Tang [8]presented rainfall threshold of loess landslides based on three infiltration models in rainfall. Ma et al. [9] combined numerical simulation with in situ observations to analyze the rainfall infiltration law in shallow loess and demonstrated that rainfall duration and intensity are most sensitive factors affecting water saturation and slope instability.
In the meantime, direct shear tests under low confining pressure provided unsaturated strength for soil and anisotropic fractured rock mass (Kim et al. [10] and Yang et al.[11]). It can be clearly seen that the augment in water content could cause drop in the cohesion and friction angle. Fu et al. [12] proposed a model for soil softening accounting for temporal variation in strength parameters. When Cheng et al. [13] presented the relationship between water content and shear strength for Q3loess. Han [14]examined loess landslides due to rainfall and its mitigation.
In summary, so far there are only a few works available on the stability of loess slope taking account of seepage-stress coupling. The circumstance motivates us to devote this study on rainfall-induced landslides of loess slope to gain an insight into its mechanism.
A seepage-stress coupling model of rainfall-induced landslide is formulated by Eq. (1) along with initial and boundary conditions in Eq. (2) as below:
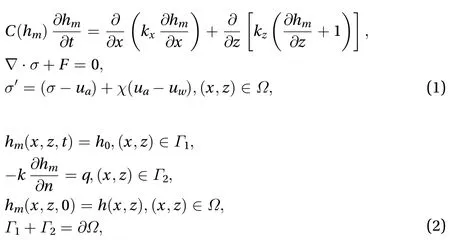
When dealing with slope boundary conditions like Eq. (2), we assume that (1) when the rainfall intensity is less than the saturated hydraulic conductivity of soil, there is no runoff generation and the infiltration rate is equal to the rainfall intensity; (2) when the rain is stronger than the saturated hydraulic conductivity of soil, the infiltration rate is equal to the saturated hydraulic conductivity of soil. Although this model can be regarded as an approximation of the rainfall-infiltration such as Green-Amp model [6], it seems to be fairly satisfactory for the application in loess landslide studies according to lots of previous calculations.Then, we have:

In addition, we employ representative empirical formula(Van Genuchten model) and Garder permeability function to link suction head and water content:


For slope instability analysis, the strength reduction method is used in this study and a reduction factorshould be defined at first. As the reduction factor is increasing, the calculation continues until the soil reaches the critical failure. The reduction factor at this moment is called the safety factor, as shown in Eq. (6).

Analyses for both steady state and transient seepage conditions were performed on a slope inclined at 53° with the height of 15 m. Figure 1 shows the slope geometry and calculation mesh in modeling. Along the left and right boundaries beneath the groundwater table, a constant head of 12 m is assumed. On the other hand, a zero flux boundaries are applied along the left and right sides above the groundwater table. Naturally, the vertical direction of the slope is an infiltration boundary. An X-X section in the middle of the slope is selected to monitor the temporal and spatial variations of pore water pressure in the process.
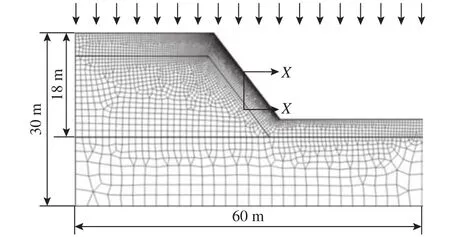
Fig. 1.Finite element mesh and boundary conditions of the slope.
Unevenly distributed rainfall of Yulin is only 570 mm annually, which is concentrated in the rainy season from July to September, almost accounting for 75% of the annual amount.The actual rainfall history in Yulin in July, 2017 is used in modeling. The rainfall intensity was recorded as: 60 mm/day in the first 3 days and 200 mm/day in the 5th and 6th days with one whole day pause in-between.
Table 1 shows the soil strength parameters of local loess in Yulin used in the calculation. Because of its special structure and developed vertical joints, loess usually is assumed to be anisotropic, which is reflected in the difference in the horizontal and vertical hydraulic conductivity.
Figure 2 demonstrates the variation of safety factor versus time, which drops sharply on the first day, nearly keeps constant and then reduces to below 1.05 with additional two days heavy rain. At this moment, the extremely unstable slope is prone to landslide. The phenomena can be attributed to the macro-pore structure of loess soil.
Now let's first intuitively view water motion inside the slope by looking at the nephogram variation of water content there.The soil initially was relatively dry and water content ascended quickly with the infiltration of rainfall. Figure 3 illustrates that one more consecutive days of heavy rain enforce rain infiltrate deep into the ground so that the slope soil becomes saturated.And then followed underwater table rise.

Table 1Soil strength parameters of local loess in Yulin.
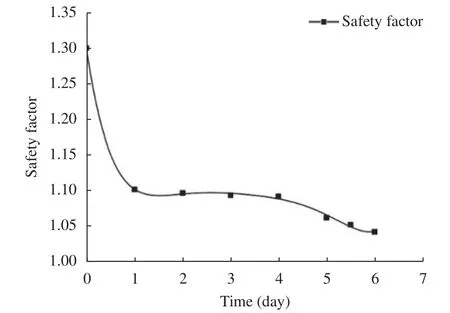
Fig. 2.Safety factor evolution versus time during the actual rainfall process.
Moreover, the pore pressure increased correspondingly, as shown in Fig. 4. It can be clearly observed that the pore pressure at the slope surface, which is very low before this rainfall due to the dry soil, was gradually increasing until saturated when torrential rain started.
Figure 5 exhibits pore pressure profiles inside the slope at section X-X. The rainfall of the first day is responsible the rise of pore pressure at the slope surface from -180 kPa to -50 kPa.However, lower pore pressure inside the slope is attributed to the fact that rain had not yet been infiltrated to the site depth.Since the rainfall was suspended on the fourth day, we can see that the soil at the upper layer dried a bit with no water supply and the infiltration in the soil of deeper layer continued under the action of gravity. With the onset of a particularly heavy rainstorm on the fifth day, the pore pressure at the slope surface instantly rose and even close to saturation. The saturation of upper soil lead to the rise of pore pressure of the lower soil in the slope due to the infiltration and the slope stability becomes extremely poor.
Based on the seepage-stress coupling model we employed,we have accomplished the modeling of rainfall infiltration process in a typical slope of local loess in Yulin according to the actual rainfall scenario in July of 2017. The simulation exhibits the slope would be considerably unstable through six days of rainfall, which is in accord with the disaster report released by the Yulin administration at that time, namely, the arrival of this torrential rain indeed triggered many landslide events.
For a deeper understanding of rain induced landslides, we simulate the variation of water content, pore pressure inside soil body with the declining in corresponding safety factor for different scenarios of rainfall. In particular, we further consider the consequence brought about by soil weakening or softening so as to gain an insight into the mechanism how rain infiltration affects slope stability.
Based on the seepage-stress coupling model, the effects of rainfall intensity on slope stability are demonstrated. Figure 6 displays the variations of safety factor versus rainfall intensity in five days of continuous precipitation for a slope with initial water content of 5%, 10%, 15%, and 20%, respectively. The safety factor of loess slopes is diminishing with rainfall intensity.However, initial water content evidently aggravates the situation so that the slope is immediately on the verge of instability.

Fig. 3.Water content distribution after 5 days of rainfall.

Fig. 4.Pore pressure contour after 5 days of rainfall.
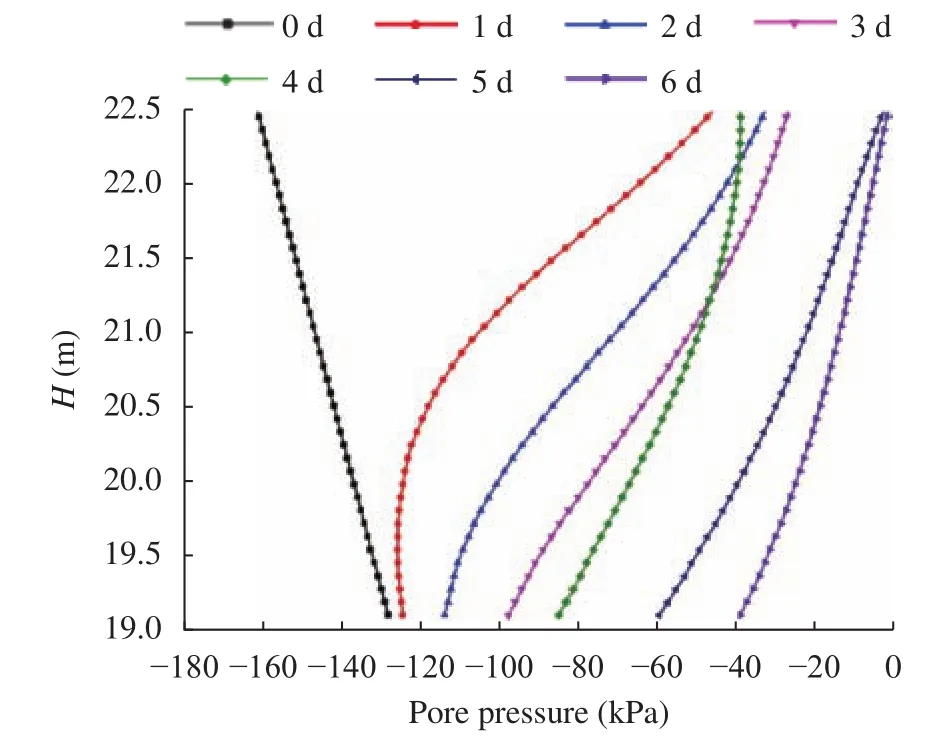
Fig. 5.Pore pressure profiles in section X-X during rainfall in Yulin.
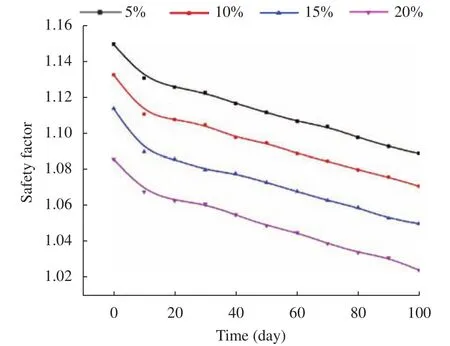
Fig. 6.Safety factor evolution versus rainfall intensity.
Figure 7 shows the pore pressure diagram for five days of consecutive rainfall at 20 mm/day, 40 mm/day, and 60 mm/day with an initial water content of 5% and 20%. Naturally, the pore pressure inside the slope and infiltration depth grows with rainfall intensity. Although the variation for higher initial water content of 20% seems to be less distinct than that for lower initial water content of 5%, the slope of higher initial water content turns out more likely to slide for intense rainfall in reality.
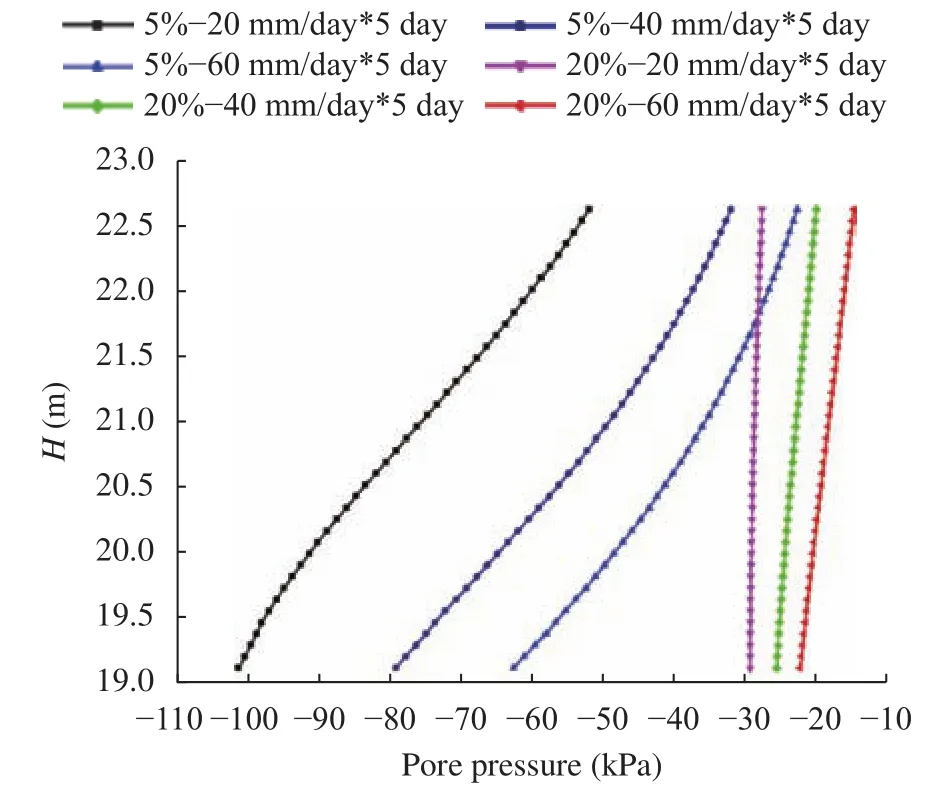
Fig. 7.Pore pressure profiles in section X-X with different rainfall intensity under the initial water content of 5% and 20%.
Similarly, we discuss the influence of rainfall duration of 50 mm/day on slope stability for slopes with different initial water contents of 5% and 20%.
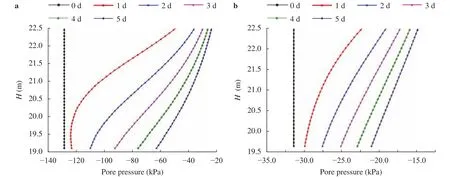
Fig. 9.a Daily pore pressure profile with rainfall intensity of 50 mm/day under the initial water content of 5%. b Daily pore pressure profile with rainfall intensity of 50 mm/day under the initial water content of 20%.
For continuous rainfall, Fig. 8 illustrates that the slope safety factor markedly declines on the first day and then keeps descending regardless of initial water content. As a result, longer rainfall certainly leads to less safety factor.
Again we would like to exhibit pore pressure profiles inside the slope body in Fig. 9. In the case of lower initial water content of 5%, the pore pressure observably grows from -128 kPa to -50 kPa on the first day and then continues to gradually rise. In contrast, the variation of pore pressure in the slope from -31.5 kPa to-22.5 kPa for initial water content of 20% is not so apparent due to less infiltration though, the slope is certainly more critical for landslide.
Anyway, as the rain gradually infiltrates into the interior of the slope with longer duration of rainfall, the distribution of water content and pore pressure become more uniform. The slope is on the verge of failure and very probably a landslide might take place.
Actually, dramatic change in the stress strength or even its constitutive behavior of soil for different saturability might occur. Hence, further examination on the effects of soil weakening is necessary. The strength parameters of soil as the functions like Eq. (7) are provided in the literatures [13, 14]:

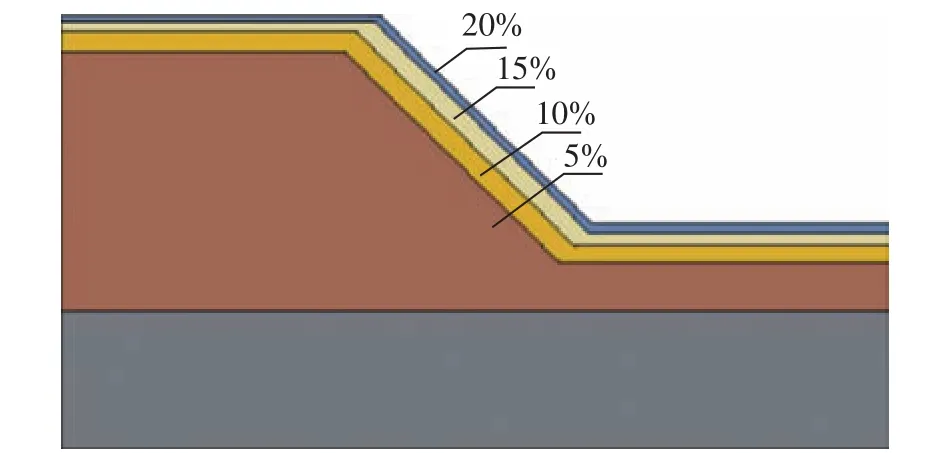
Fig. 10.Simplified water content distribution after the same rainfall scenario.
We still take the same typical slope in Yulin as an example and calculated the seepage field of the slope in the same rainfall scenario at first. When the spatial variation of water content in soil is given, the slope soil can be divided into a number of layers according to its water content as shown in Fig. 10. At the same time, we are able to find corresponding strength parameters for each layer of local loess in Table 2.
To explore the effects of seepage-stress coupling accounting for soil weakening, we have simulated three cases by considering (1) only weakening in cohesion, (2) only weakening in friction angle, and (3) weakening in both cohesion and friction angle. Figure 11 gives the variation of safety factor with time foruneven slope strength. The results are displayed in Fig. 11.

Table 2The shear strength of soil corresponding to different water contents.
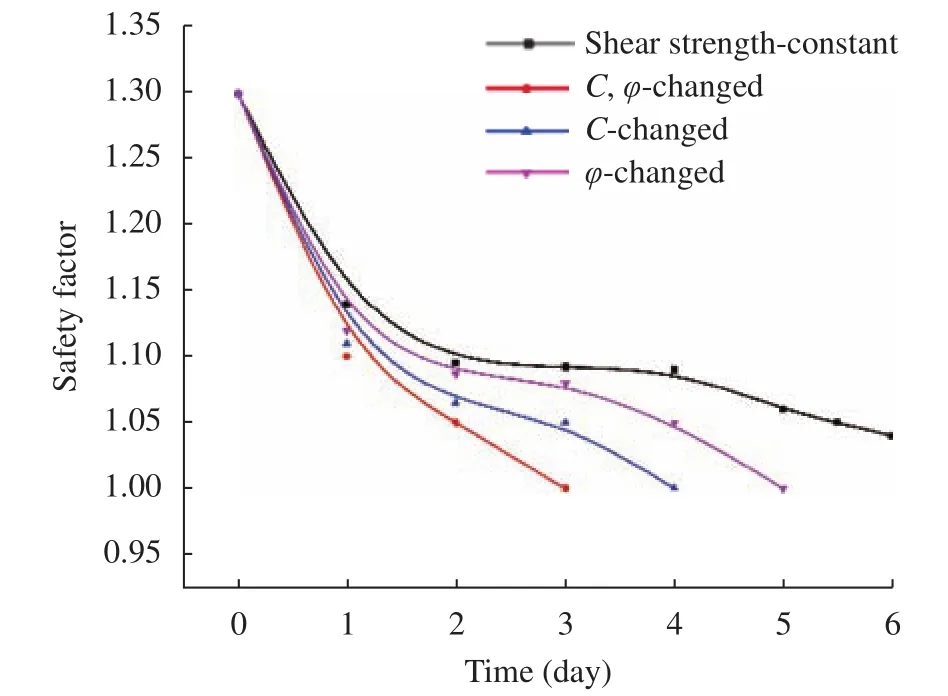
Fig. 11.Change of safety factor with time under uniform and uneven slope strength.
The safety factor of the slope generally declined from 1.3 to 1.04 on the sixth day of rainfall. In contrast, the safety factor of the slope descends more rapidly when soil weakening effects is considered. For instance, the safety factor tends to 1.05 on the second day and even less than 1.0 on the third day. In addition,the weakening in cohesion is found more sensitive to slope instability than friction angle.
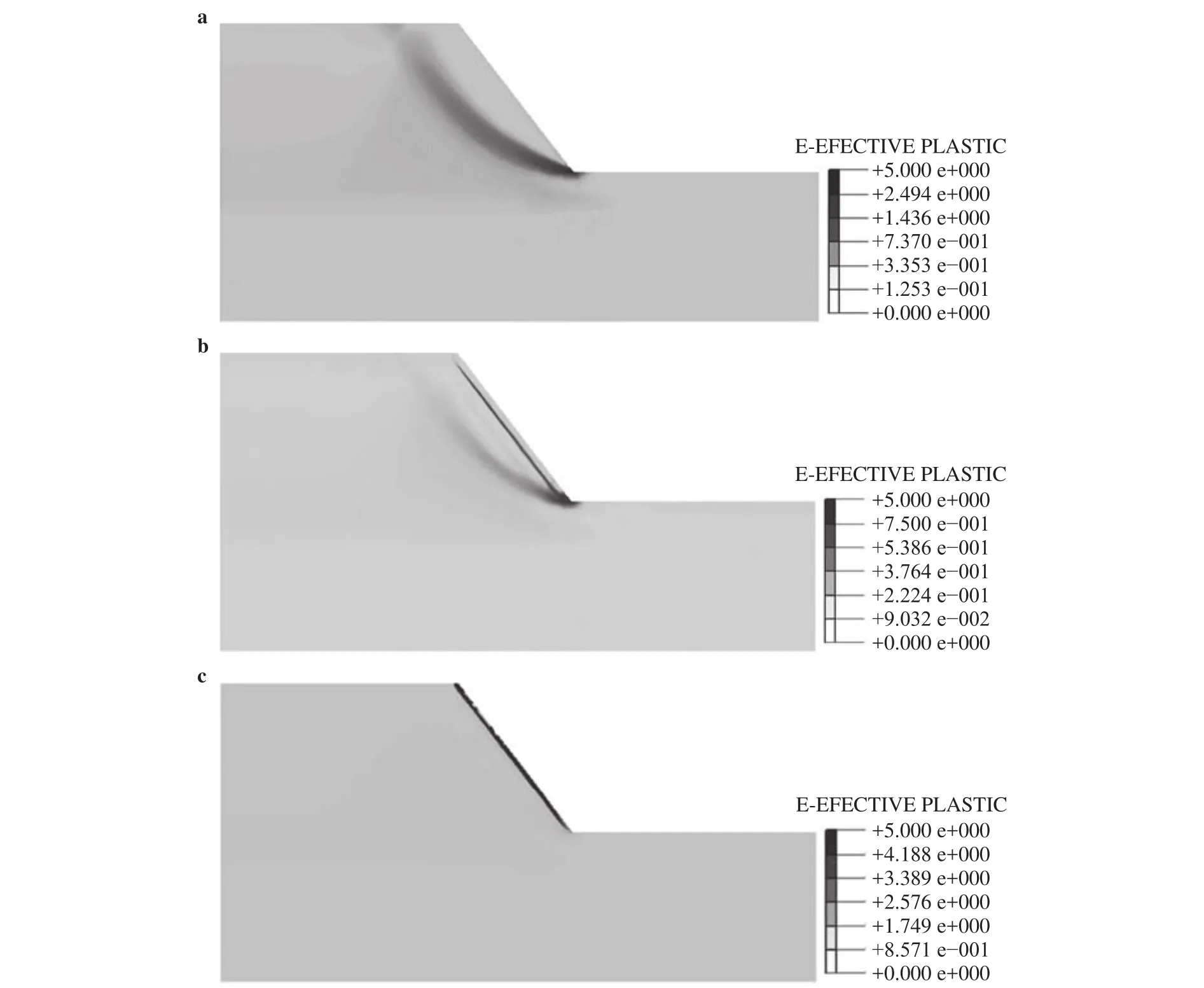
Fig. 12.a Effective plastic strain cloud diagram of slope after 1 day rainfall with weakening effect. b Effective plastic strain cloud diagram of slope after 2 days rainfall with weakening effect. c Effective plastic strain cloud diagram of slope after 3 day rainfall with weakening effect.
Let us look at the status of plastic strain cloud on each day.Figure 12(a-c) demonstrate that the effective plastic strain all starts at the foot of the slope. Moreover, it almost penetrates the loess slope on the second day and the slip zone appears on the third day, which is responsible for why the safety factor drops so dramatically when soil weakening is taken into account.
Loess landslides, which often trigger catastrophic disasters of western China in rainy seasons are still not well-understood.Hence, a seepage-stress coupling model is used to examine hazard's occurrence, evolution and implied mechanism in this study. Numerical modeling is fulfilled for a typical slope of local loess experiencing actual rain process of July, 2017 in Yulin. The simulated results lead us to come to the following conclusions.
(1) Loess slopes when subjected to a heavy rain are prone to instability and landslide. The consequences are primarily attributed to very special macropore and developed vertical joint structure so that the process of precipitation infiltration deep into slope tend to be instant and then landslides take place.
(2) The first role of rain is to fill in a layer of loess through these pores and fissures, then water content and pore pressure increase immediately. The followed reduction in effective stress would lower the resistance capability of a slope to sliding. We further analyze the effects of rain intensity, rain duration and initial water content on slope stability or safety factor. At the same time we can no longer neglect significant role of initial water content.
(3) As a matter of fact, the stress strength or constitutive relationship of soil is heavily dependent on water content, which is so-called soil weakening or softening previously neglected.Based on the given cohesion and friction angle functions on water content in literatures, we found that soil weakening would further all the more aggravate slope instability and the cohesion seems to be a more sensitive factor than friction angle.
In a word, the model of soil weakening due to water invasion is still unclear [15]. However, it at least reflects the change of failure mode from deep slide to shallow slide, which is more close to reality of loess landslide. This might open another door to reveal how to model progressive landslide and transition to debris flow.
Acknowledgements
The authors are grateful to the financial support by the National Natural Science Foundation of China (11432015 and 11602278) and the Key Laboratory for Mechanics in Fluid Solid Coupling Systems (LMFS) Foundation of Young Scientist.
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Lattice Boltzmann model of percutaneous drug absorption
- Dependency of gamma oscillations in E/I neuronal network on illumination contrast of external stimulus
- An energy approach to predict electromigration induced grain rotation under high current density
- Optimal control of a mobile robot on sphere
- Key structure in laminar-turbulent transition of boundary layer with streaky structures
- Electrokinetic flow in the U-shaped micro-nanochannels
