Lattice Boltzmann model of percutaneous drug absorption
2019-03-07ArmanSafdariKyungChunKim
Arman Safdari, Kyung Chun Kim*
School of Mechanical Engineering, Pusan National University, Busan 46241, Republic of Korea
Keywords:Lattice Boltzmann method Bhatnagar-Gross-Krook (BGK)Single relaxation time Advection-diffusion Convection-diffusion equation (CDE)
ABSTRACT A lattice Boltzmann numerical modeling method was developed to predict skin concentration after topical application of a drug on the skin. The method is based on D2Q9 lattice spaces associated with the Bhatnagar-Gross-Krook (BGK) collision term to solve the convection-diffusion equation (CDE). A simulation was carried out in different ranges of the value of bound γ, which is related to skin capillary clearance and the volume of diffusion during a percutaneous absorption process. When a typical drug is used on the skin, the value of γ corresponds to the amount of drug absorbed by the blood and the absorption of the drug added to the skin. The effect of γ was studied for when the region of skin contact is a line segment on the skin surface.
The importance of absorption rate has gradually been increasing, and interest has grown in mathematically modeling convection-dispersion transport phenomena after applying a drug to the skin. Percutaneous drug application is common in orthopedics and dermatology [1, 2]. Many researchers have studied the pharmacokinetics after applying a drug on skin [3, 4].Suitable models of drug absorption are in high demand for predicting the accurate amount of diffusion through the skin, especially for clinical applications.
Normally, a drug is continuously distributed on the skin and is administered with sufficient frequency to reach the vessels under the skin. When a significant and constant amount of drug is applied, the dose on the skin is always higher than the amount under the skin. The increase of drug in the skin layers at a decreasing rate as more and more doses are applied once the steady-state condition of the drug dose in the skin is reached. In the steady-state condition, the drug distribution should be the same throughout the portion of skin during a given dosing interval. However, the concentration depends on the diffusion, and the normalized skin capillary clearance can vary [5].
In the past, mathematical models of percutaneous drug absorption have been suggested, such as linear and nonlinear dual sorption models [6]. Another mathematical model predicts nonlinear percutaneous permeation kinetics of timolol [7]. A finite dissolution solution for a suspension model has also been developed [8]. A one-dimensional mathematical model was developed for percutaneous drug absorption [9]. Most of these models are one dimensional, the contact boundary between the skin and the drug is assumed to be a single point, the drug is diffused in one direction, and it is measured with respect to the distance into the skin.
One of the main aims of the present study is to model the linear behavior of percutaneous drug absorption while assuming the region skin contact to be a point or a line segment. An efficient numerical method was obtained to handle the discontinuity between the initial and boundary conditions. The lattice Boltzmann method (LBM) is proposed for modeling percutaneous drug absorption. LBM presents the evolution of the solute transport using diffusion distribution functions. This model is computationally robust and applicable to diffusion problems. In addition, it directly simulates the change of transport of a dilute solute and involves a low-order moment that provides high numerical stability.
The Bhatnagar-Gross-Krook (BGK) LBM is based on distribution functions that are applied for drug transport in skin. Macroscopic fluid quantities such as concentration are obtained by solving the solute distribution functions. The solute component has no velocity of its own, and the drug is carried through the skin according to the diffusion coefficient. The governing equa-tion of the LBM model for the convection-diffusion equation(CDE) is given by:

The LBM equation consists of a collision term (right-hand side of Eq. (1)), which describes the collision of the particle distribution function, and a streaming term (left-hand side of Eq.(1)), which represents the propagation of the distribution function after the collision term. R(x, t) is the source term [10], and we assume there is no reaction during percutaneous drug absorption. There are a few schemes for the collision term, but the most efficient one is the BGK collision model because of its simplicity and low cost of computation. The BGK model has a single relaxation time, and its equation is [11]:
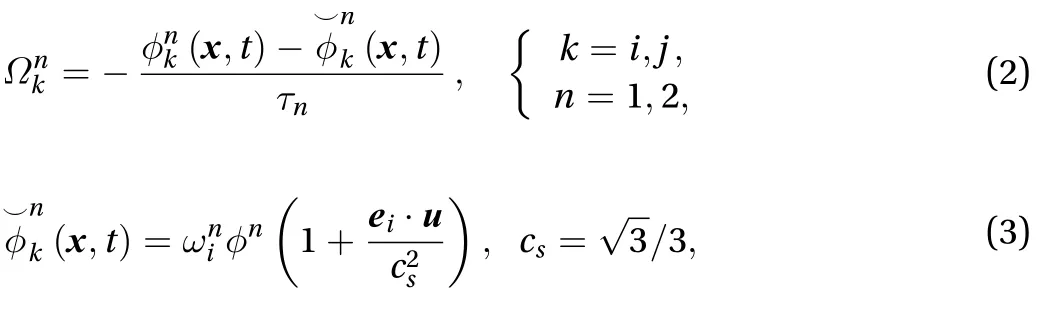

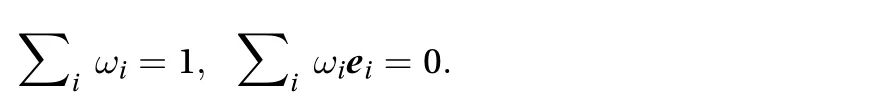
In the propagation step of the LBM after the collision term,the analytical solution of the streaming term is:
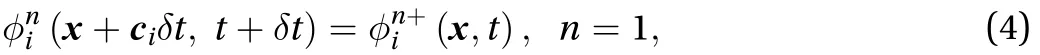
D2Q9:
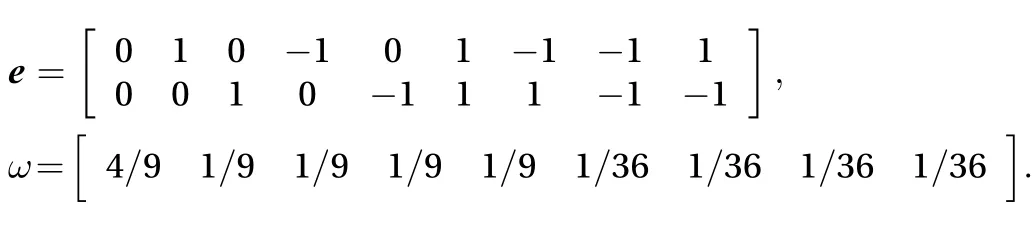
Through Chapman-Enskohg expansion, we can find the diffusion coefficient D in lattice units from the incompressible Navier-Stokes (N-S) equations associated with the single dimensionless relaxation timefor each component [10]:

The corneum, epidermis, and upper dermis have noticeably dissimilar transport and physical characteristics, and dispersion through the dermis could be a critical point in percutaneous absorption prediction, at least for some kinds of drugs. The numerical model was developed based on the typical view that the molecules of a drug are rapidly detached by the capillaries once they are separated into the dermis. Consequently, the skin-capillary boundary might functionally be interpreted as the stratum corneum-dermis boundary.
If we assume the drug is an ointment on the skin, for a onedimensional model, the contact area between the skin and the ointment drug is assumed as a point with constant value for the whole period of the percutaneous absorption process. However,for a two-dimensional scheme, the thickness between the skin surface and skin-capillary boundary are assumed to be a surface in the ranges of 0≤x≤xnand -Ld≤y≤Lu, where the contact border between the drug and skin is a line with constant concentration at time t. To predict the percutaneous absorption along the skin using the LBM model, we assume the skin is an isotropic medium with the same diffusivity in both directions. Therefore, the diffusion coefficient D can be obtained from a single relaxation time using the following equation:

The concentration of the drug is:

where Ydand Yuare positive real numbers at the border between the skin and drug.
It is assumed that the drug is applied as an ointment on the skin-surface in the range of 0≤y≤Ycat 0≤t with a constant value of M0. Therefore, two boundary conditions need to be applied between the ointment drug and skin surface: a zero diffusive flux boundary for -Yd≤y<0 and Yc<y≤Yuand a constant concentration boundary for 0≤y≤Yc. For the zero diffusion flux boundary, the unknown values of the distribution function can be obtained such that zero solute diffusive flux is maintained in the direction normal to the boundary lines. By assuming that the diffusive solute equals zero,

where n is the unit vector normal on the skin-surface.
Regarding the Cartesian lattice velocities vectors ei, the form of contribution offor i in Ref. [1] is unknown. If we assume that the unk′nown directional concentrations have the form of φi= ωiφ, wheredenotes the residual amount of concentration needed to satisfy the zero gradient condition, then Eq. (7)can be written as:

Therefore, we have

Finally, the unknown directional concentrations can be solved based on our assumptions:
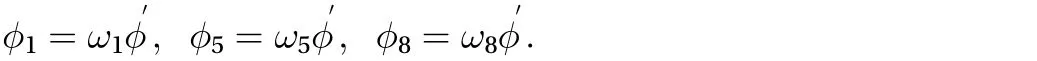
However, for 0 ≤ y ≤ Yc, a specified constant concentration M0at the boundary between the skin surface and drug must be applied. As a result, the unknown directional concentrations,,andcan be solved after the streaming term by assuming that they are ofthe form. We can compute the residual concentration as:
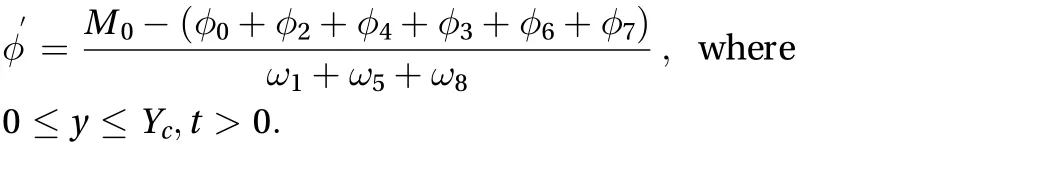
The unknown directional concentrations can be solved as:
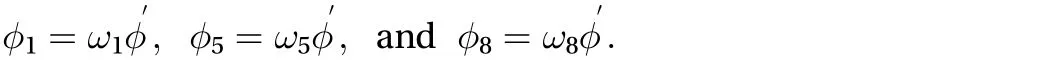
The zero diffusion flux boundary is applied in the region associated with the skin, {0 ≤ x ≤ xn, y = -Yd, t > 0} and {0 ≤ x ≤ xn, y =Yu, t > 0}. We need to do the same procedure explained before in order to apply the zero diffusion flux boundary. After some mathematical calculation, the unknown directional concentrations can be found:
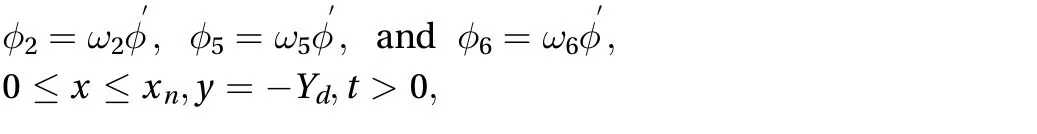
where
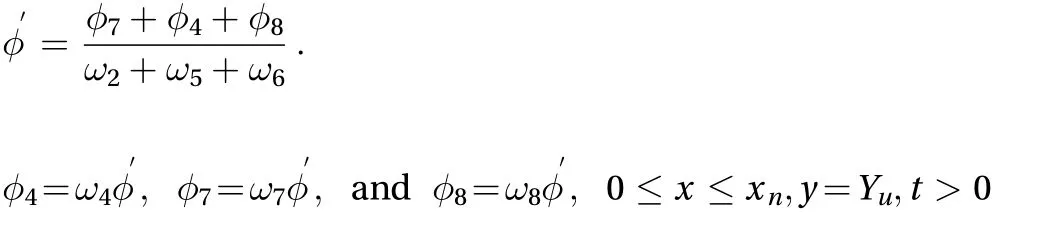

where For the subcutaneous layer after the dermis layer. the boundary condition for the LBM model is given by:
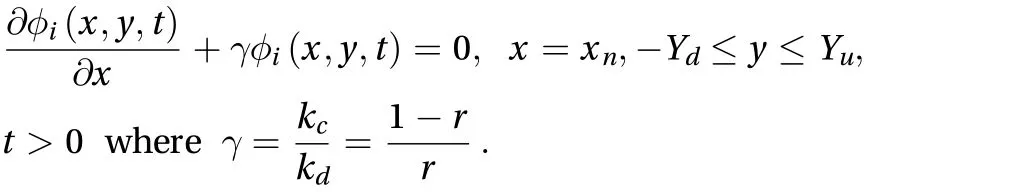
The normalized skin-capillary clearance is kc, and the diffusion parameter and concentration at the skin-capillary boundary are defined as kdand r, respectively. The approach for obtaining the numerical solution is the first-order finite different method, which leads us to the following solution:
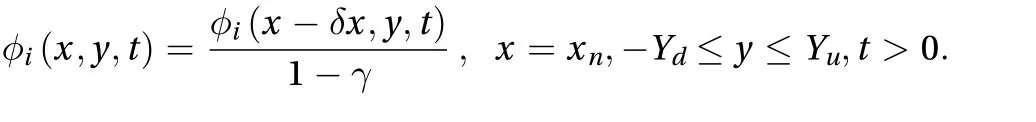
For one-dimensional numerical prediction, a constant concentration boundary is used for the contact point between the skin and the ointment drug. However, at x = xn, the boundary condition is given as:
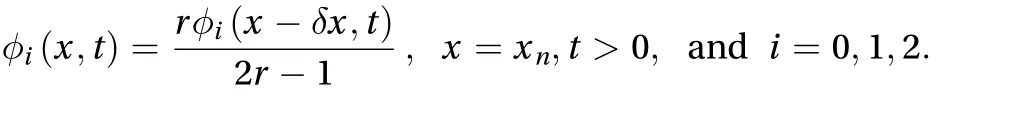
If assuming that no drug is applied on the skin, the initial concentration distribution at t=0 equals zero. The flux through the skin to the receptor area can be calculated as:
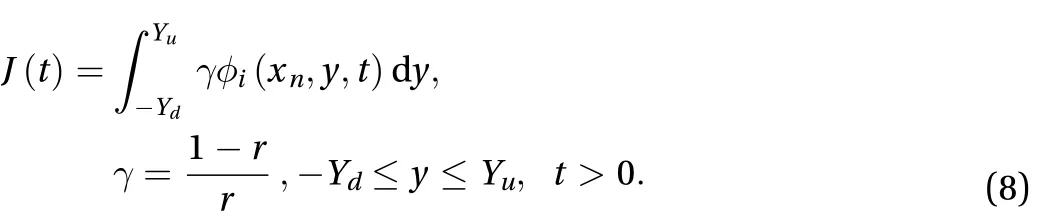
The cumulative amount of drug absorbed into the receptor cell per area at a specific time is given by:
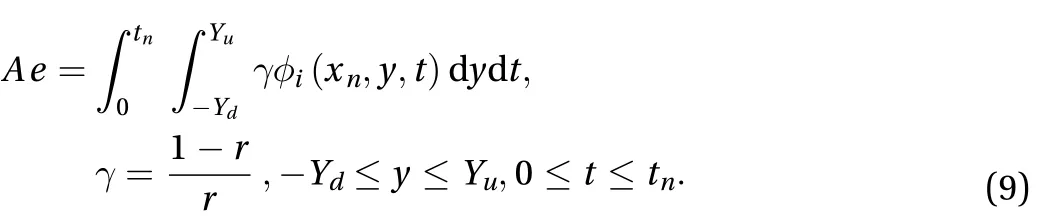
In order to verify our code, two examples are first presented and compared with the LBM simulation results. These include a 2D plane source and bonded plane source with extended initial sources. Then, the suggested model for percutaneous drug absorption is presented. Steady state is reached if the following convergence condition is fulfilled:
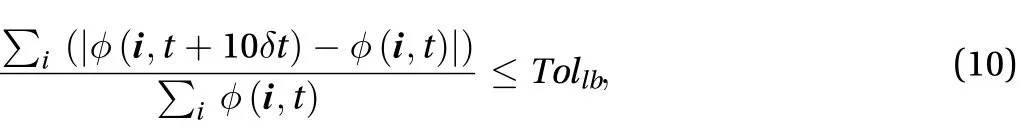
where Tollbis a tolerance set to 10-8.
In the bounded domain problem with extended initial sources, one-dimensional diffusion in a finite domain of length L is considered in which all the diffusing material is initially concentrated in a plane. The curve is reflected at x = L/2 and x = 0. In the initial conditions, it is assumed that there is no flux of diffusion along the line, which is given as:
The analytical solution of the infinite domain in diffusion can be obtained by applying the Laplace transform method [12]:
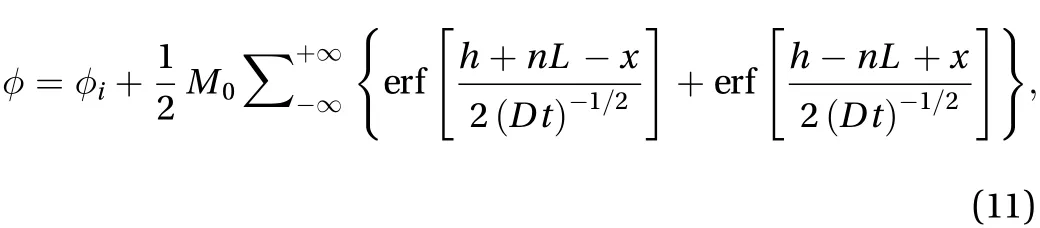
The D1Q3 scheme of LBM was applied in simulations. Different simulations results were captured at different iterations, for which the LBM parameters were,, and M0=1. A lattice size of 0.01 was fine enough to obtain accurate results. A comparison between the numerical and exact solutions of the problem is shown in Fig. 1, which proves that LBM can predict the results with high accuracy.
After validation of the one-dimensional results, a two-dimensional unbounded domain from an instantaneous point source in an infinite domain was investigated. The analytical solution is given by [13]:
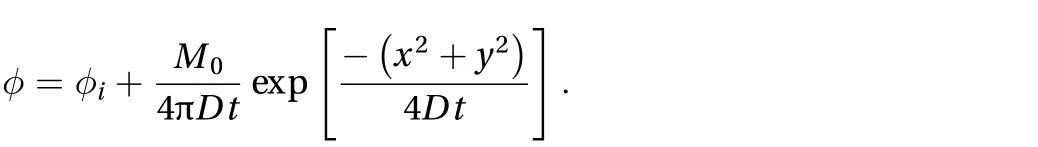
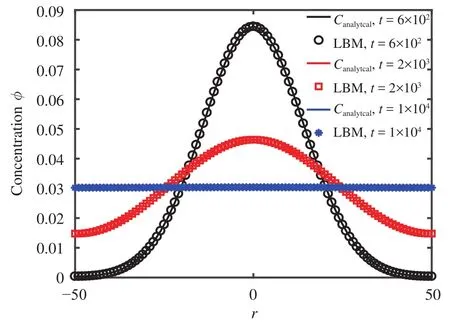
Fig. 1.Concentration distributions for a finite domain.
The D2Q9 scheme was used, and the LBM parameters were,, and M0=1. The lattice size was set as 201×201,and an interpolated boundary condition was used at the horizontal and vertical boundaries. Figure 2 shows a comparison between the numerical and analytical solutions.
In order to observe the performance of the LBM prediction of percutaneous drug absorption, a number of numerical configurations were used for the two and one-dimensional schemes. Differentvalues of 9, 1, 0.25, 0.111, and 0.053 were applied, which correspond to r values of 0.1, 0.5, 0.8, 0.9, and 0.95, respectively.Also it is assumed that Ld= 2.5, Lc= 1, and Lu= 3. The concentration profiles obtained using LBM at t = 100, 250, 500, and 750,corresponding to= 9 is shown in Fig. 3. The D1Q3 and D2Q9 schemes were used, and the LBM parameters were Ds= 1/6,=0, and M0=1. Also, the number of lattice spaces for two dimensions in the x direction and y directions are 11 and 31, respectively.
The effect of the parameter r along the skin in one space dimension can be seen in Fig. 4. Figures 5 and 6 show the effect of r on the cumulative of drug absorbed into the receptor cell Aeand the flux through the skin to the receptor area J(t). The major features relating to r are the drug molecular weight and lipophilicity, which are different for every drug, so controlling r is very difficult.
There are several factors in selecting the best drug and best ointment design, but in this study, r is assumed to play the main role in the concentration profile, and it has been used to demonstrate the prediction by the LBM model. In Figs. 4 through 6, the concentration flow rate near the skin surface is smaller than that towards the skin-capillary boundary for any value of r. Also, the difference between these concentrations increases for smaller values of r at a lower speed compared to larger values of r.
In Fig. 6, the cumulative rate of drug removed and the flux into the receptor cell are plotted. The flux and cumulative amount of drug drop at a particular time as the value of r grows, and the steady-state condition for a smaller value of r can be obtained faster than for a larger value of r. The maximum absorption of the drug into the blood veins occurs at the smallest values of r.
In this study, an LBM numerical model associated with the BGK collision term was used to predict skin concentration after topical application of a drug on the skin. The D1Q3 and D2Q9 lattice spaces were applied to solve the CDE along the skin for one and two-dimensional models, respectively. Simulation of the numerical model was carried out in different ranges of,which is related to skin capillary clearance and the volume of diffusion during a percutaneous absorption process.
Fig. 2.Diffusion from point source in an unbounded domain at t=2000.
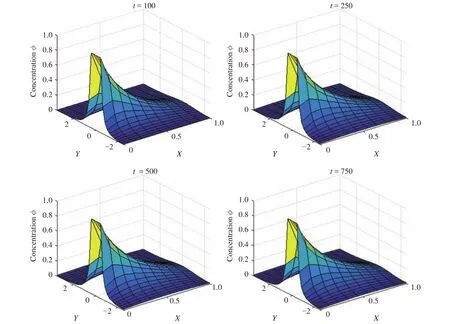
Fig. 3.Concentration profile at different iteration for = 9.

Fig. 4.Concentration profile along the x direction for different values of r.
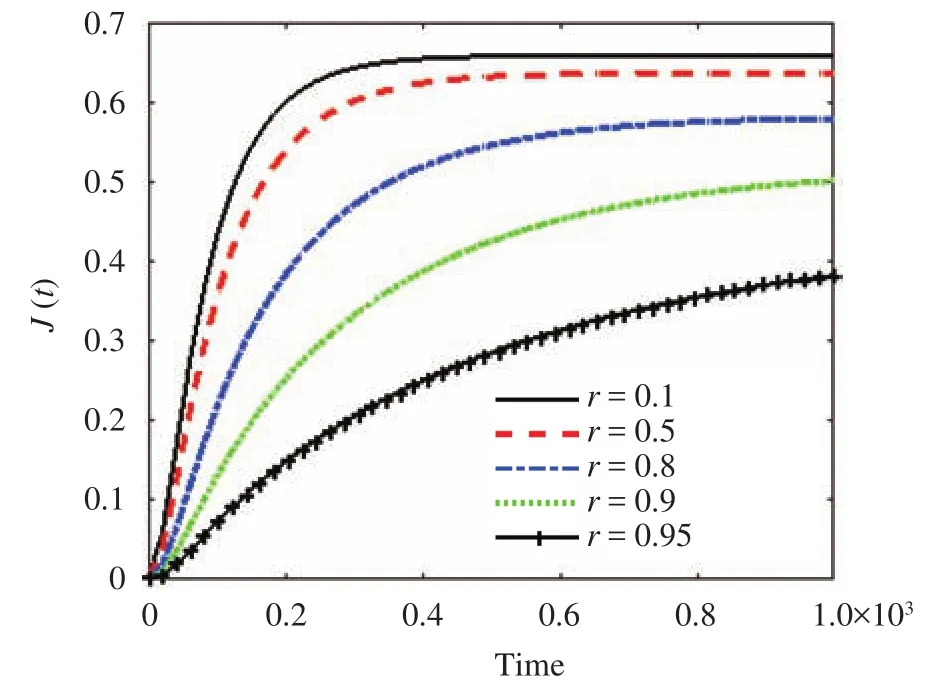
Fig. 5.The flux of drug through the skin versus time for different values of r.
The simple model prediction is mostly accurate in spite of the complexity of the skin structure. However, the predictions of the model might be different from practical observation if the main assumptions do not hold. The diffusion through dermis is considered as a critical component, so drug diffusion through the dermis in the y-direction is important, and the prediction of the present model might be different from the observed results.However, we believe that the model might be capable of examining the diffusion mechanism in the y-direction.
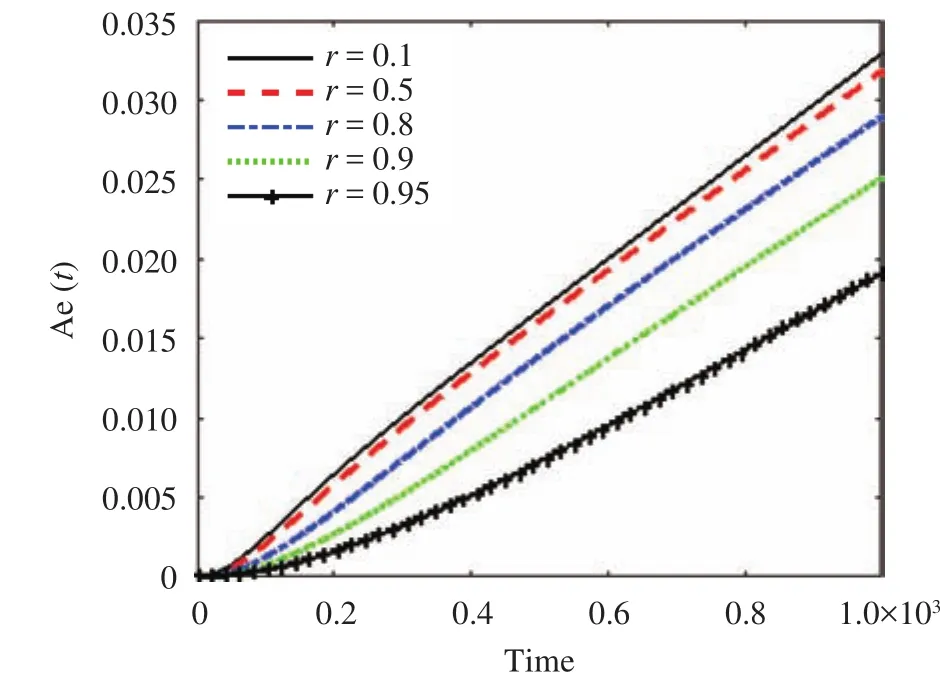
Fig. 6.The cumulative amount of drug eliminated through the skin versus time for different values of r.
The model is considered as a linear model since the drug permeation profiles inside the skin are the same. However, if we assume that the drug molecules are either dissolved or immobile through the skin, the drug permeation profiles would be different from a linear model, and we would need to apply a nonlinear model for correct prediction, which will be studied in future work. The LBM model does not allow for the complex physiology of the skin and the kinematic behavior of the drug at the site distance from where the ointment is applied, since it was developed by simplifying the skin layers.
Acknowledgment
This research was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (2011-0030013 and 2018R1A2B2007117).
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Seepage-stress coupled modeling for rainfall induced loess landslide
- Dependency of gamma oscillations in E/I neuronal network on illumination contrast of external stimulus
- An energy approach to predict electromigration induced grain rotation under high current density
- Optimal control of a mobile robot on sphere
- Key structure in laminar-turbulent transition of boundary layer with streaky structures
- Electrokinetic flow in the U-shaped micro-nanochannels
