《平行线性质综合应用》教学案例
2019-03-06福建省泉州第十一中学王世晶
福建省泉州第十一中学 王世晶

本节课的主要内容是平行线性质的综合应用,既是对上一节课平行线性质的巩固提升,也是加深对性质的理解和应用。初一学生都具有好奇、好问的探究心理,创设问题情境,能够迅速激发学生的兴奋点,并且使学生把知识的学习当作一种自我需求。
本节课教师作为一个引路人,通过一个图形进行多种变式设问,引发学生心理上的认识冲突,然后把探究的机会交给学生,充分调动学生的学习积极性、培养他们的创新意识、体现新课程理念下的交流与合作。
片段一:课前预习题:如下图,已知AB∥CD,猜想∠BPD与∠B、∠D的关系,说明理由。
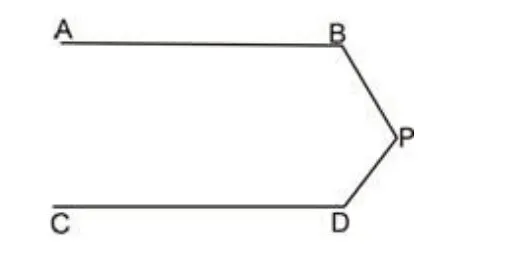
要求同学以小组为单位课前讨论,尽可能给出不同的解法,上课时每组投影展示并讲解比赛。比赛规则是:解法和解答问题正确次数多为获胜组。因为要比赛,同学们的积极性都比较高,课前都做了充分准备。
上课一开始,同学们就进行了你争我赶的展示、讲解,气氛非常活跃,教师即时就各组的解答进行点评,每一小组都猜想正确,但方法不一,共有以下5种解法。
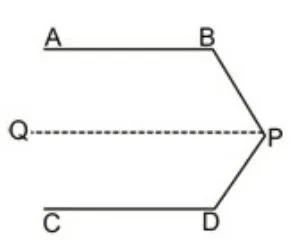
图1
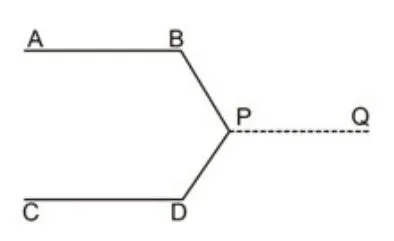
图2

图3
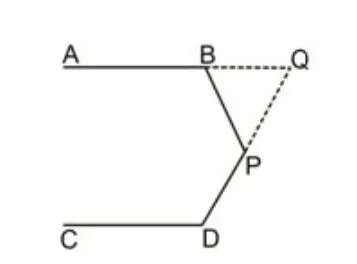
图4
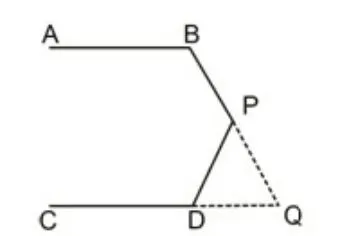
图5
解法1:过P向左边作平行线PQ,利用“两直线平行,同旁内角互补”性质可得(如图1)。
解法2:过P向右边作平行线PQ,利用“两直线平行,内错角相等”性质和“周角定义”可得(如图2)。
解法3:连接BD,利用“两直线平行,同旁内角互补”性质和“三角形内角和”可得(如图3)。
解法4:延长DP交AB的延长线于Q点,利用“两直线平行,同旁内角互补”性质和“三角形内角和”以及“平角定义”可得(如图4)。
解法5:与解法4类同,延长BP交CD的延长线于Q点(如图5)。
片段二:例题:如下图,已知AB∥CD,猜想∠BPD与∠B、∠D的关系,说明理由。
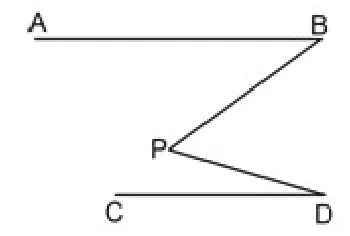
要求同学仿照预习题的方法尽可能给出多种解答,由于时间关系,要求以抢答形式,且每组只能抢不同的方法。
气氛再次高涨,答案一个接一个地写在黑板上,几乎是标准答案。
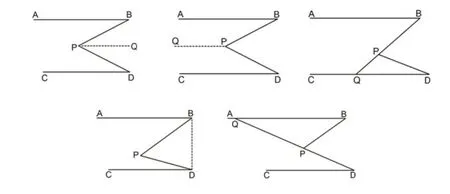
片段三:教师乘胜追击提出了新问题,请同学们比较课前预习题与例题,它们只是图形发生了改变,条件和问题都相同。仔细观察这两个图形的结构特征,能否再次改变图形,编制新题。课堂一下子沉静了,教师抓住时机引导学生观察这两个图形:它们无非是两条平行线与三个角,把∠P看成可以上下、左右运动,把两条平行线看成可以左右平移,那么图形将如何画出?请各小组马上开始讨论并展示。
不一会儿,各组争先恐后地绘出以下各图。


教师、同学们都满意地笑了,那么如何解答呢?时间已经不允许了,本题作为今天的作业。
教学后记:学生的学习过程既是一个认知的过程,又是一个探究的过程。在教学中,通过对一个图形巧妙变式地创设问题,使学生在疑中生奇、疑中生趣,不断激发学生的学习欲望和主动探究的意识,引导学生以小组为单位进行合作探究,可以创设和谐、宽松的课堂氛围,让每位同学都不脱离队伍,让每位同学都真正参与活动,强化了学生的主体意识,培养了学生的合作精神,也体现了团结、友爱、互帮互助的集体氛围。
学习终究是学生的事,学习的效果取决于学生是否愉快地融入集体中,是否真正参与探究活动中,是否积极主动地思考;教师只是一个组织者和引导者,教师的责任更多是为学生提供合作的平台,为学生创设思考的机会,为学生留有思考的时间;正如新课程理念所倡导的“尊重学生的需要,关注学习过程”。
本节课教师通过探究平行线性质的综合应用,放手让学生合作、猜想、探究、类比、归纳,使不同层次的学生都得到应有的收获。

