移动质量法结合分形维数的旋转梁损伤检测
2019-03-06韩伟毛崎波田文昊
韩伟,毛崎波,田文昊
(南昌航空大学 飞行器工程学院,南昌 330063)
0 引 言
在航空工程中,有很多梁结构处于旋转运动状态,例如螺旋桨、涡轮叶片等。这些结构长期在复杂恶劣的自然环境中处于高强度、高负荷运行状态,容易出现裂纹损伤,因此,对这些结构进行健康监测十分必要。基于振动的损伤检测技术具有无损、实时、高效等优点[1],已得到国内外学者的广泛关注。常见的检测方法大都围绕模态振型或者固有频率而展开[2-3]。基于模态振型的方法(例如曲率模态法、柔度曲率法等)虽然能够有效地定位损伤,但是其损伤指标的获取需依靠模态振型,必须进行大量试验,费时费力。
当结构发生损伤时,其固有频率会发生变化,因此利用损伤前后固有频率的变化可以进行损伤识别。相比模态振型,固有频率在试验中更容易获得,而且精度较高。然而基于固有频率的损伤检测方法存在一定的局限性:(1) 易受环境噪声影响,抗噪能力较弱;(2) 难以识别损伤位置和损伤程度。为了解决上述问题,Zhang Y等[4-5]、Zhong Shuncong等[6]提出了一种通过移动质量块得到系统的固有频率曲线的方法,用以检测圆筒管道结构的损伤情况,且通过实验表明移动质量法能够有效地识别出损伤位置,所需传感器少,布置灵活方便,实用性较强;2016年,Wang L等[7]利用移动质量法对几种铁路轨道的损伤情况进行了研究;Chen Y等[8]也提出了基于固有频率曲线和小波分析相结合的方法来检测梁结构的损伤情况。但是关于旋转梁结构的损伤识别研究仍相对较少,李录平等[9]提出了风机叶片裂纹损伤定位方法,通过比较摆振方向上的前两阶振型的振型变化量对损伤进行定位。
上述关于移动质量法的研究均是通过与小波分析相结合的方式,由于旋转梁结构的损伤通常发生在局部位置,而分形维数在几何上能表征一个物体的局部不规则性,本文采用移动质量法结合分形维数理论进行旋转梁结构的损伤检测,研究裂纹位置、损伤程度、附加质量块大小以及转速对损伤检测的影响,最后讨论多裂纹情况的损伤检测。
1 质量块-裂纹梁模型
以变截面旋转梁为基础建立质量块-裂纹梁模型,如图1所示。梁的长度为L,梁的密度和弹性模量分别为ρ、E,转轴半径为r,转速为Ω,梁截面为矩形,其高度h(x)和宽度b(x)沿x轴方向减小,可以表示为
(1)
(2)
式中:h0和b0分别为梁固定端截面的高度和宽度;ch和cb分别为高度和宽度的渐变系数。
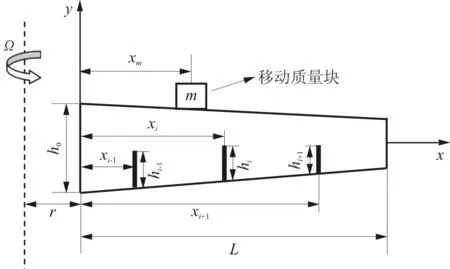
图1 质量块-裂纹梁系统
梁上含有h个开口裂纹和一个可移动质量块,第i个裂纹距梁固定端的距离为xi,深度为hi;质量块质量为m,距梁固定端的距离为xm。由文献[10]可知,裂纹可用无质量扭转弹簧模拟,如图2所示。
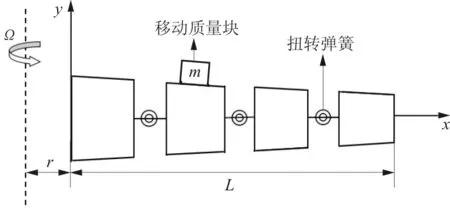
图2 离散模型
基于欧拉-伯努利梁理论,第i段完整梁的横向自由振动微分方程[11]为
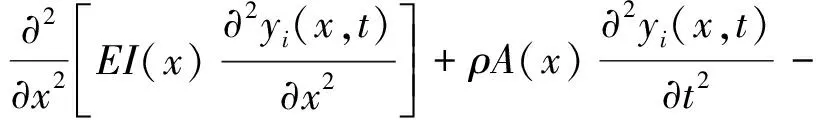
(3)
式中:x∈[xi-1,xi];A(x)和I(x)分别为横截面积和惯性矩。
A(x) =b(x)h(x)
(4)
(5)
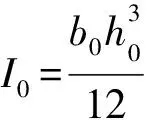
T(x)为旋转梁所受离心力,可表示为
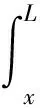
(6)
根据振动分析理论可知,梁的横向位移函数可分离为空间函数和时间函数,即方程(3)的解具有如下形式:
w(x,t)=φ(x)eiωt
(7)
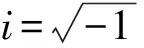
将式(7)代入式(3)进行变量分离并将变量无量纲化,可得:
(8)
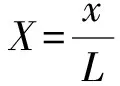
根据Frobenius理论[12],第i段完整梁的自由振动位移为
Φi(X)=N1iF1(X)+N2iF2(X)+N3iF3(X)+
N4iF4(X)
(9)

裂纹梁边界条件为
(10)
(11)
由文献[10]可知,在第i条裂纹处连续性条件为
(12)
式中:Xi为裂纹相对位置,Xi=xi/L;θi为梁的第i条裂纹引起的无量纲柔度[13]。
θi=5.346h0·J(si)
(13)


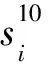
(14)
式中:si为相对裂纹深度,si=hi/h0。
由于式(13)中的无量纲柔度θi为J(si)和固定端截面高度h0的函数,必须给定梁的固定端截面高度h0才能得到无量纲柔度θi。
质量块处连续性条件为
(15)
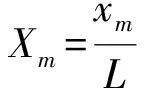
联合边界条件、裂纹处连续性条件、质量块处连续性条件可以得到由4(n+2)个方程组成的齐次线型方程组:
K(λ)N=0
(16)
式中:

N=[N11N21N31N41…N1,n+2N2,n+2N3,n+2N4,n+2]T。
因为方程(16)存在非零解,故得到频率方程:
|K(λ)|=0
(17)
由式(17)可解出无量纲固有频率λ。
2 数值模拟
当质量块在梁上移动时,结构的固有频率会发生改变。当质量块移动到裂纹位置附近时,由于局部质量增加,引起局部刚度下降,裂纹附近的固有频率降低。质量块会放大裂纹损伤对固有频率的影响。因此,利用移动质量法所得的固有频率曲线包含结构损伤信息。
2.1 分形维数理论
分形理论是现代数学的一个分支,它反映了复杂形体占有空间的有效性[14]。目前,分形维数理论[14-17]在几何、地理、生物等领域均有广泛的应用。Higuchi通过修改Burlage和Klein的算法,提出了一种用于计算时间序列分形维数的算法[18]。具体计算步骤如下:
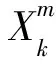
(18)
每一个重构序列的曲线长度为
可用重构序列长度的平均值近似表示初始序列长度:
(19)
对于不同的k值,可求出k与L(k)的关系:
L(k)~k-FD
(20)
对式(20)两边取对数,可得:
(21)
式中:C为常数;FD为该时间序列的分形维数。
在时间序列曲线上开设定尺度窗口,计算窗口内曲线段的FD,均匀拖动窗口,可得到关于FD的曲线,称为HFD曲线。
2.2 损伤检测
选取质量块-裂纹梁系统(如图1所示)为研究对象,假定无量纲转轴半径R=0,固定端截面高度h0=0.02 m,高度渐变系数ch=0.3,宽度渐变系数cb=0.1。应用移动质量法结合Higuchi分形理论进行损伤检测,并分别讨论裂纹位置、损伤程度、质量块大小以及转速对损伤检测的影响。
2.2.1 损伤位置识别
假设裂纹梁的无量纲转速U=3,无量纲质量α=0.3,相对裂纹深度s=0.3,裂纹相对位置分别在Xc=0.2~0.8处,画出Xc分别为0.2、0.4、0.6、0.8这四种损伤工况下的第一阶无量纲固有频率曲线,如图3(a)所示,可以看出:随着裂纹位置向自由端移动,固有频率逐渐增大,然而却无法直接判断裂纹位置。
根据Higuchi分形理论计算固有频率曲线的HFD曲线,如图3(b)所示。
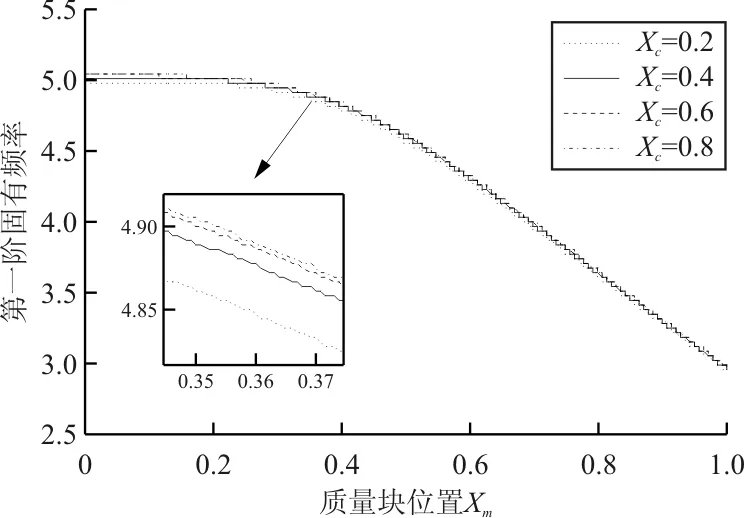
(a) 第一阶固有频率曲线
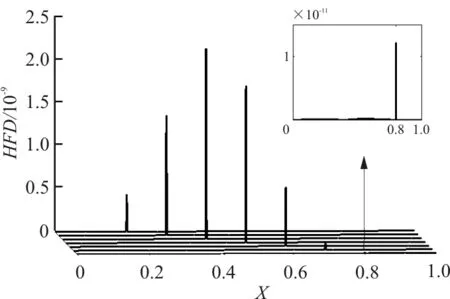
(b) 不同裂纹位置的HFD曲线
从图3(b)可以看出:在各裂纹处HFD曲线均有明显峰值出现,曲线峰值随着裂纹位置向自由端移动而呈现出先增大后减小的趋势,表明Higuchi分形方法能够准确地识别出损伤位置。
2.2.2 分形方法对损伤程度的敏感性
假设裂纹梁转速U=3,无量纲质量α=0.3,裂纹相对位置在Xc=0.3处,相对裂纹深度s依次为0.1、0.2、0.3、0.4,计算第一阶无量纲固有频率曲线,如图4(a)所示,可以看出:随着裂纹深度的增加,其固有频率呈减小趋势。
运用Higuchi分形方法计算固有频率曲线的HFD曲线,其结果如图4(b)所示,可以看出:随着裂纹深度的增加,HFD曲线峰值逐渐升高,可见Higuchi分形方法对裂纹损伤程度具有很好的敏感性。
HFD曲线峰值与裂纹深度的关系如图4(c)所示,可以看出:HFD曲线峰值随裂纹深度的增加而呈现单调递增趋势,表明Higuchi分形方法能够定性地反映损伤程度。

(a) 第一阶固有频率曲线
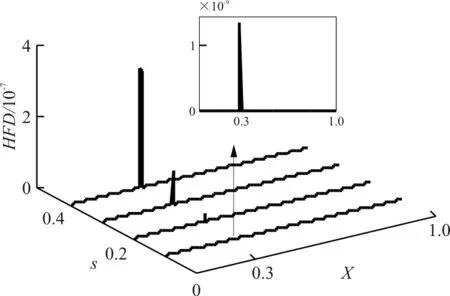
(b) 不同损伤程度的HFD曲线
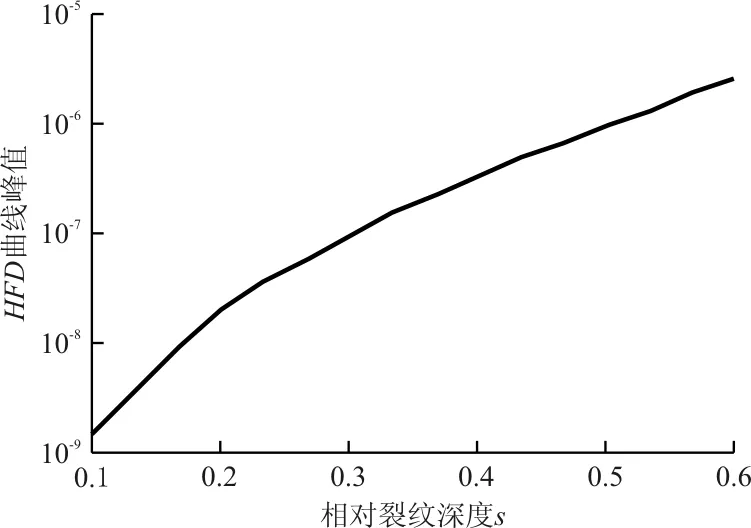
(c) HFD曲线峰值与裂纹深度的关系
2.2.3 质量块大小对损伤检测的影响
设定裂纹梁转速U=3,裂纹相对位置在Xc=0.3处,相对裂纹深度s=0.3,无量纲质量α依次为0.1、0.2、0.3、0.4,计算第一阶固有频率曲线,如图5(a)所示,可以看出:第一阶固有频率从Xm=0.2附近开始随着无量纲质量的增加而呈现减小趋势,且变化率逐渐增大。
运用Higuchi分形方法计算固有频率曲线的HFD曲线,如图5(b)所示,可以看出:随着无量纲质量α增大,HFD曲线在裂纹处的峰值也逐渐增大。
HFD曲线峰值与质量块大小的关系如图5(c)所示,可以看出:HFD曲线峰值随α单调递增,且当0.1≤α≤0.5时,曲线变化率增大;当α>0.5时,曲线变化率减小。因此,α取0.4~0.6为宜。
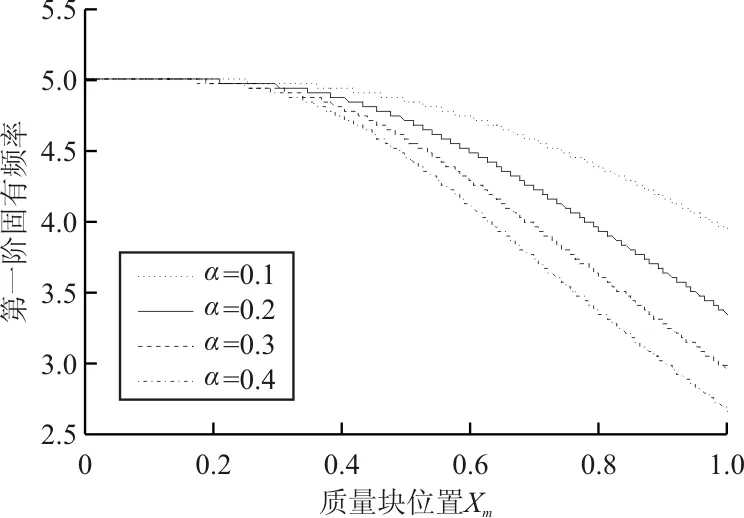
(a) 第一阶固有频率曲线

(b) 不同质量块大小时的HFD曲线
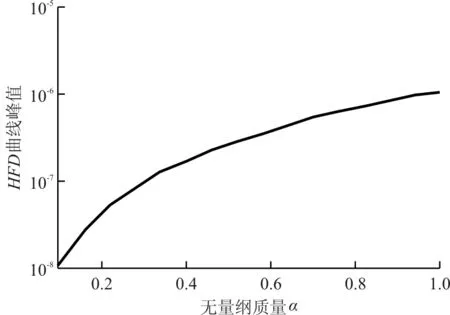
(c) HFD曲线峰值与质量块大小的关系
2.2.4 转速对损伤检测的影响
假设裂纹相对位置在Xc=0.3处,相对裂纹深度s=0.3,无量纲质量α=0.3,无量纲转速U依次为1、2、3、4,计算第一阶固有频率曲线,如图6(a)所示,可以看出:随着转速的提升,第一阶固有频率随之增大,各转速所对应的固有频率随着质量块的右移而呈现减小趋势,且从Xm=0.4开始,固有频率曲线变化率逐渐增大。
计算固有频率曲线的HFD曲线,如图6(b)所示,可以看出:随着转速升高,HFD曲线峰值也随之增大。
HFD曲线峰值与转速的关系如图6(c)所示,可以看出:当转速从0递增至8时,HFD曲线峰值单调递增;当转速从8递增至13时,曲线峰值单调递减。因此,当转速为8时损伤检测效果最佳。

(a) 第一阶固有频率曲线

(b) 不同转速时的HFD曲线

(c) HFD曲线峰值与转速的关系
2.2.5 双裂纹损伤检测
为了进一步检验本文方法对多裂纹损伤梁的有效性,以双裂纹损伤工况为例进行研究。假设裂纹1位于X1=0.2处,裂纹2位于X2=0.7处,相对裂纹深度s从0.1渐变至0.6。运用Higuchi分形方法进行数值模拟计算,结果如图7所示。(为了更清楚地看出相对裂纹深度s=0.1、s=0.2的损伤检测结果,给出局部放大图,如图7(b)、图7(c)所示。)
从图7(a)可以看出:随着裂纹深度的增加,HFD曲线的峰值逐渐增大,表明在双裂纹损伤工况下,Higuchi分形方法对损伤程度仍然具有敏感性。
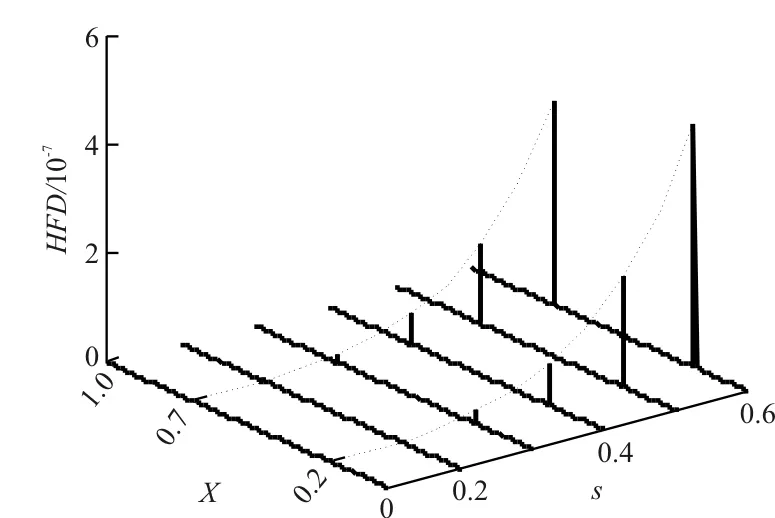
(a) 不同损伤程度时的HFD曲线
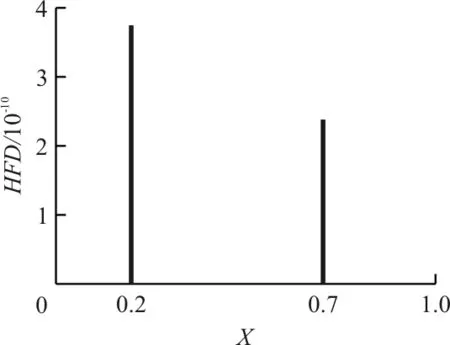
(b) s=0.1
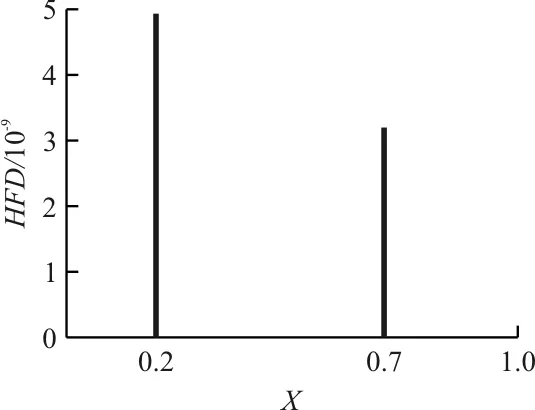
(c) s=0.2
3 结 论
(1) 本文提出的将移动质量法与分形维数理论相结合来进行损伤检测的方法,能够准确地识别出损伤位置,并且对裂纹损伤程度具有很好的敏感性,能够定性地反映出损伤程度。
(2)HFD曲线峰值随无量纲质量α单调递增,且当0.1≤α≤0.5时,曲线变化率增大;当α>0.5时,曲线变化率减小,因此,α取0.4~0.6为宜;当转速从0递增至8时,HFD曲线峰值单调递增,当转速从8递增至13时,曲线峰值单调递减,因此当转速为8时损伤检测效果最佳。
(3) 对于多裂纹损伤工况,本文方法同样适用,对损伤程度仍然具有敏感性。
