无穷直线上k解析函数的非正则型Riemann边值问题
2019-03-05曾伟
曾 伟
(西南民族大学预科教育学院,四川 成都 610041)
解析函数的边值问题是复变函数论中的一个重要分支.在文献[1]中,路见可教授系统的总结了前人关于解析函数的相关知识.在文献[2]中,维库阿·依·涅提出并研究了解析函数的推广─广义解析函数.文献[3],杨丕文教授提出了k解析函数,并进行了初步研究.文献[4-7]进一步研究了k解析函数的性质和多种不同类型的边值问题.k解析函数大大地扩充了解析函数的古典理论及其应用范围.本文将在文献[3-7]的基础上,研究无穷直线上的k解析函数的非正则型的Riemann边值问题.
1 问题的提出
定义1[3]:设G是复平面上的一个区域,k为自然数,u(z)∈Ck(G),且在G内有

此时,称u(z)在G上是k解析的,或者称u(z)为G上的k解析函数.
定义2:设L是一条直线,并且是无穷的.不妨假设此直线为x轴,记为X,并且与x轴方向相同.为了便于理解,不妨把复平面的上半平面记为Z+,复平面的下半平面记为Z-.设fj(ζ)∈,简记为(其中0<α ≤1,j= 0,1,…k-1). 定义 Cauchy型积分:

当z∉X时,W(z)是k解析函数.
引理1[3]:设W(z)是区域G内的k解析函数的充要条件是W(z)可表示为

其中,Wm(z),(m =0,1,…,k-1)是G内的解析函数,并且W(z)在G内如(2)的表达式唯一.
引理2[5](Plemelj公式):设fm(t)∈(m =0,1,…,k-1).当z从Z+与Z-内分别趋于t(t∈X)时,极限值

定义3:求在Z+,Z-内分片k解析函数W(z)(W(∞)有界,且W±(+∞) = W±(-∞)),使得W(z),在X两侧可以连续延拓到X上,并且满足

其中,G∗(t),f0(t),f1(t),…,fk-1(t) ∈,并且G∗(t),在X上可以有一些整数阶的零点,称之为k解析函数在无穷直线X上的的非正则型的Riemann边值问题,可以简称为R问题.
文献[5]中讨论了正则型G∗(t)≠0的情况,本文讨论非正则型,即在X上可以有一些整数阶的零点.假设,其中 G(t) ∈,且 G(t) ≠ 0,而(t- βl)μl,此处 αj和 βl在无穷直线 X 上面,同时 αj≠ βl, λj∈Z+, μl∈Z+. 令,κ为边值问题的指标.更特殊的情况是,当f(t)=f(t)=… =f(t)=0时,边值问题更加01k-1便于分析,称为齐次边值问题,简称为R0问题.下面,我们首先分析齐次边值问题,再利用这一结果,进一步讨论更一般的情况.
2 无穷直线上的非正则型的齐次边值问题
无穷直线上的非正则型的齐次边值问题R0的边界条件:

由文献[1]的方法,可得G(t)的分解


令

显然有
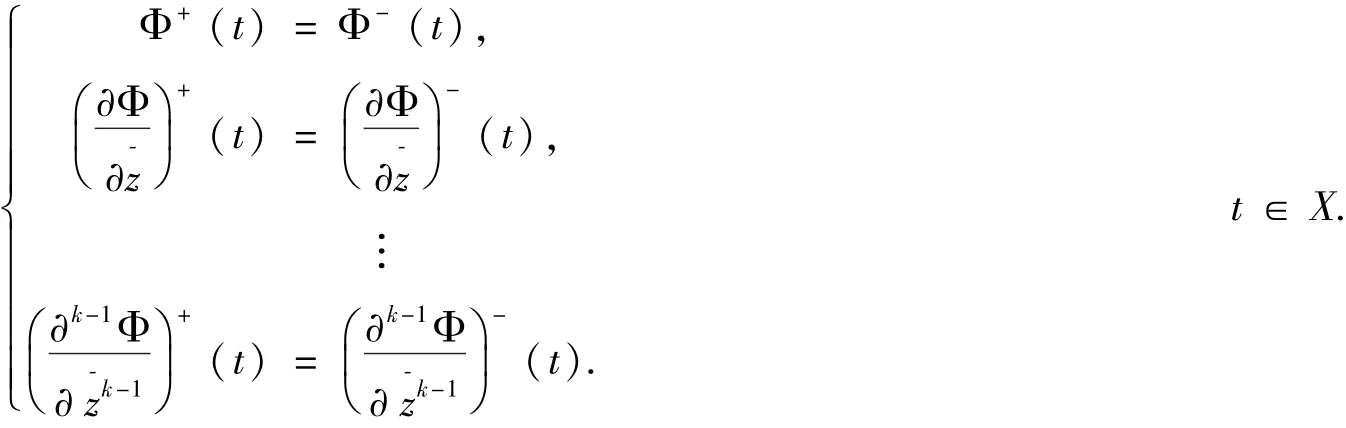
根据文献[4]的理论,函数Φ(z)在复平面上是k解析函数的.又因为W(∞)有界,并且函数F(z)在∞处具有 -κ阶,所以函数Φ(z)在∞处不超过λ+κ阶.
因此,满足边界条件(5)的非正则型齐次问题R0的解为:


其中 m = 0,1,2,…k-1 ,Pm,κ-μ-m(z) 是 κ - μ -m 次多项式(若 κ - μ -m < 0 ,则可以认为 Pm,κ-μ-m(z)≡0).所以,满足边界条件(5)的非正则型齐次问题R0的解为:

定理1:对于满足边界条件(5)的无穷直线上的非正则型的齐次问题,有
①当κ>μ时,其一般解为(10)式;
②当κ=μ时,其一般解为

其中复常数C为任意复数;
③当κ<μ时,非正则型的齐次问题只有一个唯一解,零解.
3 无穷直线上的非正则型的非齐次边值问题
无穷直线上的非正则型的非齐次边值问题R的边界条件:

用前面讨论的方法,把(6)式代入(12)式,可得


其中Γ(z)为(8)式.
对(13)式乘以 (z+i)-κ,则

令

或者

其中

由引理2可知

由(15)式和(16)式,可得

因为W(∞)有界,可得

从而,有

做 ρ= λ + μ -1次 Hermite插值多项式 Rm,ρ(z),m = 0,1,…,k-1:

这种多项式是存在唯一的.
令

所以:当μ-κ+k-2≤0时,W0(z)是满足边界条件(12)的无穷直线上k解析函数的非正则型的非齐次问题的一个特殊的解.
当μ-κ+k-2>0时,因为W0(z)有μ-κ+k-2阶极点,要W0(z)是满足边界条件(12)的无穷直线上k解析函数的非正则的非齐次问题的解,还应满足个条件,令

则
当λ+κ≥-1时,上述条件应为:

即Rm,ρ(z)只能是λ+κ-m次的多项式(当λ+κ =-1时,Rm,ρ(z)≡0).
当λ+κ <-1时,除了要求Rm,ρ(z)≡0,m =0,1,…k-1,还要保证u(z)在∞具有 -(λ+κ)阶零点,即

定理2:对于满足边界条件(12)的无穷直线上的非正则型的非齐次问题,有
①当μ-κ+k-2<0时,其一般解为W(z)=W∗(z)+W0(z),其中W∗(z)由(10)式确定,W0(z)由(18)确定;
②当μ-κ+k-2=0时,其一般解为W(z)=W∗(z)+W0(z),其中W∗(z)由(11)式确定,W0(z)由(18)确定;
③当 μ-κ+k-2 >0时,要求f0(t),f1(t),…,fk-1(t)满足个条件时,边值问题此时可解,且解是唯一,解由(18)确定.
ⓐ当λ+κ≥-1时,要求由(17)式所确定的插值多项式Rm,ρ(z)是λ+κ-m次的多项式;
ⓑ当λ +κ <-1时,除了Rm,ρ(z)≡0,m = 0,1,…k-1外,还要满足(19)式成立.
本文所得到的的结论,使得无穷直线上的k解析函数的Riemann边值问题在文[5]的基础上,从正则型的情况推广到了非正则型的情况.本文的结论更加普遍,它丰富了k解析函数的理论基础,同时使得k解析函数关于Riemann边值问题的应用更加广泛.
