时间分数阶Camassa-Holm型方程的各种精确解及其动力学性质

唐 威，冀小明

(1.重庆师范大学数学科学学院，重庆 401331；2.西南民族大学预科教育学院，四川 成都 610041)

近几十年来，分数阶非线性偏微分方程得到了越来越广泛的关注，因为它们可以用来精确的描述许多科学研究领域的一些奇特的非线性现象.例如，许多自然现象具有记忆性，事物内在的联系和变化不仅依赖于时间的瞬时性，还依赖于以往的时间历程，这些现象均可以用时间分数阶微分模型来刻画和描述;在反常扩散模型中，反常扩散现象可以用时间或者空间分数阶微分模型来加以刻画和描述;分数阶水分子向土壤的入渗以及非饱和水在土壤中的运移模型可以用时间或空间分数阶微分模型来刻画和描述;许多黏弹性流体力学问题也可以用时间分数阶微分模型来加以描述.在全面了解这些模型所赋予的动力学性质、动力学行为和动力学现象以及事物内在的联系和变化规律等方面后，模型的精确解能更好地解释和体现这些内容，因此，寻找分数阶非线性偏微分方程的精确解和近似解析解在许多科研领域得到了广泛的应用，如在流体动力学、生物科学、工程科学中的控制问题、信号处理、大气动力学、地表水力学、土壤物理、多孔介质力学、河流水力学、地下水文学和水化学等.

近年来，求解分数阶微分方程出现了许多有效的方法，这些方法包括Adomian分解法[1]、首次积分法[2]、同伦分析法[3]、李群理论方法[4]、不变子空间方法[5-6]、分式变分迭代法[7]、分数阶复变换法[8]、分离变量法[9]等等.虽然用以上的方法可以得到一些分数阶非线性偏微分方程的精确解和近似解析解，但是想要解决更为复杂的分数阶非线性偏微分方程还是远远不够的，为此，芮教授在文献[10-11]中首先提出了用变量分离法与齐次平衡原理和积分分支法相结合的方法来精确求解时间分数阶非线性偏微分方程的思想，有效的获得了一系列时间分数阶非线性偏微分方程的精确解.

经典的整数阶Camassa-Holm型方程是一类十分重要而又特别的新型浅水波方程.在这个方程中，能够找到一种尖孤立子解，从而声名鹊起，并且该模型具有广泛的应用背景.众所周知，浅水波方程在长波、小振幅条件下可得到经典的KdV方程，实践观察、数值模拟和理论分析均证明了它属于完全可积系统，具光滑的孤立波解，它的波形在相互作用中几乎保持不变，能量也几乎不损失，于是这类研究成果在信号传输中得到了广泛的应用.1993年，美国阿尔莫斯国家实验室的Camassa和Holm推导出了另一类浅水波方程的孤立波解.自从Camassa和Holm找到这种连续但不光滑的新型孤立子后，十多年来已引起了许多数学家和物理学家的关注和兴趣，他们做了大量的理论研究工作，其中包括利用孤立子理论获得该方程的各种单孤立子解和多孤立子解，利用可积性理论，证明了该方程具有双哈密顿结构，满足无穷多守恒律等.此外，Constantin等从偏微分方程定性研究的角度讨论了该方程的整体弱解、光滑解的存在唯一性和它的渐近稳定性质等问题.可见Camassa-Holm型方程在数学和物理学领域都非常重要.为了更好地理解较为复杂的分数阶Camassa-Holm型方程的非线性物理现象的机理，找到该分数阶非线性偏微分方程的精确解就显得极其重要了.因此许多学者对该方程进行了研究，例如，Guilong Gui学者研究了部分耗散的Camassa-Holm方程的全局平稳和爆破解[12];Zhenggrong Liu研究了Camassa-Holm型方程的周期爆破解及其极限形式[13];Youwei Zhang等人使用变分迭代的方法求解出了分数阶Camassa-Holm型方程的解析解[14].相对于整数阶Camassa-Holm方程的精确解研究而言，关于分数阶Camassa-Holm型方程的精确解的研究工作和文献还比较少，这是由于求分数阶微分方程的精确解往往比较困难，所以正如文献[15-16]中所提及的那样，目前大多数工作主要集中在解或者正解的存在性研究，与这类研究不同，像文献[10-11，17]那样，以下的工作将立足于分数阶微分方程在精确解方面的探索与研究.

基于文献[10-11]中关于变量分离法与齐次平衡原理相结合的思想下，来研究时间分数阶Camassa-Holm型方程的各种精确解.首先来简要地叙述一下这个时间分数阶非线性模型求解精确解的算法.

1 变量分离法与齐次平衡原理相结合的算法简介

对于一般的分数阶非线性偏微分方程：

第一步：根据许多文献求解出来的分数阶非线性偏微分方程的精确解的形式来看，大多以Mittag-Leffler函数和幂函数为主，而且都是变量分离形式的解，因此不妨假设方程(1)有下列两种形式的精确解：

其中v＝v(x)为待定函数，a0，a1，λ为待定系数，γ为待定常数，这些待定的函数和常数将在后面的计算步骤中加以确定，Eα，1(λtα)为单参数Mittag-leffier函数，它的分数阶导数，即α阶导数为(λtα) ＝ λEα，1(λtα).这两个解的假设结构式既适合Riemann-Liouville型微分算子下的偏微分方程的精确求解，又适合Caputo型微分算子下的偏微分方程的精确求解.下面以(2)式为例来说明第二步的操作.

第二步：将(2)代入到(1)中得到

根据齐次平衡原理，在方程(4)中令Eα( λtα)的各次项的系数和常数为零，得到

然后解上述非线性常微分方程组，就可以得到v＝v(x)和参数a0，a1，λ的值.

第三步：将第二步里面的非线性常微分方程组的解v＝v(x)和参数a0，a1，λ的值代入(2)式，就可以得到方程(1)的不同的精确解，最后用同样的方法，可以得到方程(1)的各种形如(3)式的精确解.

2 时间分数阶Camassa-Holm型方程的精确解及其动力学性质

本节中将用第二节介绍的方法求解下列时间分数阶Camassa-Holm型方程[12]

的精确解，其中u＝u(x，t)，t＞0，x∈R.将方程(5)改写成

如果以上两个方程中的分数阶微分算子是Riemann-Liouville型微分算子，那么假设方程(6)有如下形式的解：

其中a0，a1为待定系数并且a1≠0，γ待定常数且γ＞-1，函数v＝v(x)是关于x的待定函数.将(7)式代入分数阶非线性偏微分方程(6)后即得：

在(8)中，让t的所有幂指数相等，便得到下列普通方程

解方程(9)可得到

将(10)式代入(8)式，然后方程两边同时除以t-2α得到下列方程：

其中m的最高次可以通过齐次平衡法来确定，即平衡方程最低阶线性项v与最高阶非线性项vvxxx中关于x的最高次数，得到m ＝3.同样，若平衡高阶线性项vxx和最高阶非线性项vvxxx中关于x的最高次数，得到m ＝1.

如将m ＝3代入(12)得到

其中b0，b1，b2，b3，b4是待定系数.将(13)式代入(11)式得：

将m ＝1代入(12)式便得到

其中b0，b1为待定系数.又将(15)式代入(11)式可得：

在方程(16)中，让x的同次幂的所有系数都等于零得：

解方程(17)得到

将(18)式代入(15)式可以得到v(x)的具体形式

将(19)式和(10)式代入到(7)中，可以得到方程(6)的一种精确解：

其中a0，a1，b0是任意非零常数且且显然，在解(20)式中，空间部分的函数是一次函数，本是一个无界的函数，但时间部分的函数是一个衰减的函数，即当t→+∞时，t-α→0，所以整个解具有随时间增加而衰减的特性，同时也是随时间渐进稳定的.

通过进一步的探索与研究，发现方程(11)还具有以下形式的解：

显然当m ＝1时，(21)和(22)变成

其中 c0， c1， p0， p1， q0， q1为待定系数.将(23)式代入(11)式得：

其中

类似地把(24)代入(11)式得：

其中

在以上两个方程(25)和(26)中，分别令eωx和双曲函数的所有系数都等于零得：

和

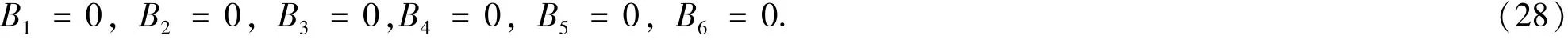
分别求解以上两个方程组，得到方程(25)和(26)恒成立的参数条件：

将(29)和(30)式分别代入(23)和(24)中便可以得到方程(11)的解：

再将(31)和(32)以及(10)式分别代入到(7)式中，得到方程(6)的两种精确解：

其中a＝a1c1，a1，p1，q1为任意非零常数.显然，解(33)和(34)的空间函数部分也是无界的函数，但时间部分却是收敛的函数，即当t→+∞时，t-α→0，所以以上两种解都具有随时间增加而衰减的特性，即当t→+∞时u→0.这表明，这两个解都是随时间渐进稳定的.为了能够直观地展示上述解的动力行为和动力学现象，运用Maple软件画出了解(33)和(34)的三维坐标图形，分别见下图1-1、图1-2，图1-3、图1-4.在图1-1和图1-2中，参数取值：a1＝2，c1＝1，β＝1，α ＝0.25.在图1-3和图1-4中，参数取值：，a＝1，p＝

111，q1＝ 2，α ＝ 0.25，β ＝ 1.

图1 解(33)和解(34)的三维肖像图Fig.1 The three-dimensional profile graphs of solution(33)and solution(34)

其中d0，d1，λ是待定常数且d0≠0，v(x)是关于x的待定函数，定义为单参数Mittag-Leffler函数.将(35)式代入方程(6)得：

在方程(36)中，让 Eα( λtα) 和的系数都等于零可得下列方程组

首先求解(37)式中第一个线性常微分方程，得到以下形式的通解：

其中有l1，l2为任意常数，将(38)式代入方程组(37)的第二个非线性常微分方程中整理得：

解得d0＝d0，d1＝d1，于是将(38)式代入(35)式，便得到方程(6)的另一种形式的解：

显然，当λ＞0时，解(41)整体是一个无界的解，即u→∞(t→+∞).而当λ＜0时，解(41)随时间增加而衰减，即u→0 (t→+∞)，即解随时间渐进稳定.以便直观的展示上述解的动力性质，画出了前面的解(20)以及解(41)的三维坐标图形，分别见下图2-1及图2-2.在图2-1中，解(20)坐标图的各参数取值分别为a0＝2，a1＝ 1，b0＝2，α ＝0.25.在图2-2中，解(41)坐标图的参数取值为λ ＝1，d1＝0.5，l1＝2，l2＝1，β ＝1，α ＝0.75.

图2 解(20)和解(41)的三维肖像图Fig.2 The three-dimensional profile graphs of solution(20)and solution(41)

3 结论

利用变量分离法与齐次平衡原理相结合的方法，获得了时间分数阶Camassa-Holm型方程的各类精确解，这些精确解的空间变量部分包含指数函数和双曲函数，这些函数都是无界的，但所有的解都具有随时间增加而衰减的动力学行为，都具有随时间增加而渐进稳定的特性.实践再次证明变量分离法与齐次平衡原理相结合的方法能够有效的获得了一系列时间分数阶非线性偏微分方程的精确解.