主、次裂隙对岩石变形破坏机制的影响研究*

2019-03-05李克钢秦庆词杨宝威

中国安全生产科学技术 2019年2期

李克钢,王庭,秦庆词,潘震,黄伟,杨宝威

(昆明理工大学国土资源工程学院，云南昆明 650093)

0 引言

岩体作为与采矿工程、地下工程、公路隧道工程息息相关的介质，不仅具有非连续性、非均质性以及各向异性，而且岩体内还存在大量的节理裂隙。外部扰动作用下，岩体内的节理裂隙易发生扩展、搭接、贯通等现象，使岩体强度降低并且易发生变形导致岩体工程失稳破坏，易产生重大安全隐患。因此，针对含裂隙岩石变形规律、强度特征以及破坏形式的研究对于生产建设过程中岩体工程的稳定性评价具有重要的指导意义。

鉴于裂隙岩体在工程中广泛分布与应用，针对于裂隙岩体力学特性、变形破坏机制以及裂隙扩展规律等方面的研究，国内外学者已进行了大量的研究工作，Iriwn[1-2]将裂纹分为Ⅰ型裂纹(张开型裂纹)、Ⅱ型裂纹(面内剪切型裂纹)、Ⅲ型裂纹(反平面裂纹或面外剪切型裂纹)3种类型；Brace等[3]通过试验得到最大主应力方向为裂隙稳定扩展方向的结论，并且提出了二维裂隙滑移开裂模型，通过模型解释了岩石破坏前的扩容现象；秦楠等[4]研究了单轴压缩下单条预制裂隙不同倾角引起的抗压强度的变化规律；蒲成志等[5-6]对含2条贯通裂隙及多条贯通裂隙试件进行了单轴压缩试验，通过对裂隙试件应力-应变曲线与裂隙面颗粒破坏形状的综合分析，研究贯通裂隙试件破坏机制；李树刚等[7]通过对预制裂隙类岩石材料试件的单轴压缩试验，研究了预制裂隙宽度对试件力学特性及破坏机制的影响规律，裂隙宽度的增加导致试件峰值强度降低，而峰值轴向应变增大；杨圣奇等[8]在大理岩试件上切割断续裂隙，并对裂隙试件进行了单轴压缩，从而研究裂隙各种参数对试件力学性质及破坏特征的影响；张波等[9]研究了主次多裂隙、等长多裂隙对类岩石材料试件强度及峰值强度对应应变值的影响，发现等长裂隙相较于主次裂隙对试件强度影响极为显著；杨涛等[10]利用双差定位算法对含裂隙的花岗岩试件压缩破坏过程中产生的波速进行分析，深入研究了荷载下岩石的破坏机理；刘东燕等[11]发现X型交叉裂隙岩体中，交叉裂隙会抑制主裂隙方向的变形，其强度要高于单一裂隙岩体；同样是X型交叉裂隙试件，张波等[12]在对其进行单轴拉伸试验后发现次裂隙的几何特征对试件强度的影响规律；杨圣奇等[13]在砂岩试件上切割出3条裂隙，研究了岩桥倾角对试件强度影响以及裂纹的扩展规律和破坏模式；李露露等[14]对三叉型裂隙进行了单轴压缩及PFC2d数值模拟试验研究，探究了裂隙间夹角对抗压强度的影响规律，得知裂隙中张拉作用影响要远大于剪切作用。显然，对于X型交叉裂隙以及平行裂隙岩桥对岩体影响的研究成果较为丰富，而近似T型相交情况作为岩体工程中重要的裂隙分布形式，其对岩体强度变形规律的影响鲜有研究。

本文对单轴压缩条件下的主、次裂隙近似T型分布的试件进行研究，从中发现裂隙夹角变化对试件影响规律，弥补当前对岩石中相交裂隙研究的不足之处，对工程实际具有一定指导意义。

1 前期准备与试验

本次试验采用类岩石材料，由石膏、经20目筛分的干河沙与自来水按质量比为1∶1∶0.75的配比均匀混合，放入特制钢模具中制成外观尺寸为100 mm×100 mm×100 mm的试件。插入厚度为0.3 mm的薄钢片，模拟天然岩石中所含的闭合贯通裂隙。在试件养护前期拔出预埋的金属薄片。脱模后进行为期1周的养护并进行打磨处理。主裂隙的倾角都为45°，主裂隙布置在试件的正中心位置，以30 mm长单裂隙试件为例，具体形式如图1(a)所示。

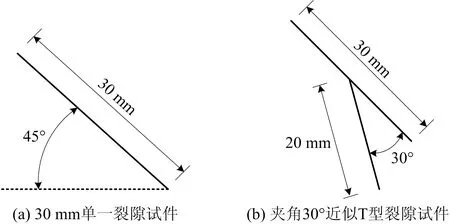
图1 裂隙试件Fig.1 Crack specimens

裂隙试件的主裂隙长度为30 mm，角度为45°，设置次裂隙长度为20 mm，次裂隙端部交于主裂隙中点。交叉角度选择30°，60°，90°方式布置。以30°试件为例，具体裂隙布置形式如图1(b)所示，每种试验方案测试3块试件，试验方案如表1所示。

表1 试验方案设计Table 1 Test plan

本次单轴压缩试验采用长春朝阳试验仪器厂生产的TAW-2000D微机控制电液伺服岩石三轴试验机。轴向最大试验力2 000 kN，最大围压100 MPa。单轴压缩加载时先用0.002 mm/s的加载速度控制接触，接触力设定为1 kN。其后用500 N/s的速度加载至试件破坏。

2 试验结果及分析

对方案1～4试件进行单轴压缩试验，获取4种方案下试件的峰前应力-应变曲线，并观察试件压缩破坏过程中裂隙扩展发育状况，从多组结果中取峰值强度最接近均值试件组的结果进行分析说明。

图2 裂隙试件峰前应力-应变曲线Fig.2 Pre-peak stress-strain curve of crack specimens

2.1 裂隙试件应力-应变曲线

应力-应变曲线如图2所示，由于试件所采用的类岩石材料经过充分的搅拌混合，使得所制成的试件材料结构较为致密、空隙度较小，故图2中无法观察到明显的压密段曲线，而峰前的线弹性段持续时间较长，线弹性段与屈服段可以明显观察到。由于次裂隙的存在，试件峰前变形量得到了拓展，达峰值强度时，含次裂隙试件变形量较单一裂隙试件均有不同程度的提升，且变形量随夹角减小而增大。同时发现当接近试件峰值强度时，夹角越小，塑性变形阶段的曲线愈为平缓，试件塑性特征有所衰减。

不同夹角的次裂隙存在导致了试件峰值强度与弹性模量均产生明显差异，如图3所示。单一裂隙试件峰值强度明显高于主、次裂隙试件。裂隙试件交叉夹角度数与强度差异关系为90°>60°>30°。单一裂隙试件弹性模量为6.2 MPa，而增加次裂隙后对试件的变形产生了较大影响。当应力加载到1 MPa左右时，4条曲线的斜率出现了明显差异，且随应力水平的增加，含主、次裂隙试件曲线的斜率出现更大幅度的衰减。

图3 单轴强度-夹角-弹性模量Fig.3 Uniaxial strength-angle-elastic modulus diagram

2.2 裂隙试件破坏模式分析

单一裂隙试件裂隙扩展模式如图4(a)所示，随应力水平的增加，预制裂隙上端最开始出现翼型裂隙1，当翼型裂隙1即将发育到试件顶部时，预制裂隙下端的翼型拉裂隙2开始发育，最终形成1条连接翼型裂隙1，预制裂隙和翼型拉裂隙2的贯通裂隙，导致试件的破坏。

(预制裂隙1—主裂隙，预制裂隙2—次裂隙)图4 单一裂隙及含主、次裂隙试件破坏模式Fig.4 Failure mode of single crack and T-type crack specimens

还可以看出，翼型裂隙开始发育时近乎垂直于预制裂隙，裂隙扩展到近端部时，延伸方向逐渐趋于平行最大主应力方向。这是由于应力加载初期，驱使裂隙尖端扩展的作用力为造成裂隙之间相对错动的有效剪力，故预制裂隙面上发生相对错动。平行于裂隙的张拉作用力迫使裂隙尖端产生张拉破坏，出现翼型裂隙。翼型裂隙在应力持续增加的过程中，受最大主应力作用影响增强，试件的破坏模式逐渐趋于平行轴向应力方向的张拉破坏；交叉夹角为30°时，破坏过程如图4(b)所示，随应力水平的提升，主裂隙上端部首先产生了翼型拉裂隙1及试件右侧1条因端部效应而产生的拉裂隙2。当翼型拉裂隙1即将扩展至试件顶部时，次裂隙底部产生了翼型拉裂隙3。翼型拉裂隙1，3分别扩展至试件两端，形成1条由翼型拉裂隙1，预制裂隙1和预制裂隙2形成的组合裂隙；交叉夹角为60°时，发生与30°交叉夹角试件相同变化。同样由主、次裂隙端部分别扩展的翼型拉裂隙1，2以及组合裂隙形成的贯通裂隙面，导致试件的破坏，如图4(c)所示； 90°交叉夹角试件破坏模式与30°，60°夹角试件不同。随应力增长，主裂隙两端分别产生了翼型拉裂隙2，3。翼型拉裂隙1发展到试件底部后，翼型拉裂隙2，3分别扩展至试件的两端，最终形成倒Y型裂隙模式，如图4(d)所示。

3组不同夹角的近似T型裂隙试件均在其主裂隙外侧尖端产生了应力集中，从而萌生翼型拉裂隙沿最大主应力方向扩展直至贯通试件顶部。30°与60°夹角裂隙在通过内侧相交节点后，均选择拉剪破坏作用更为明显的次裂隙方向进行扩展，形成1种组合裂隙破坏模式，如图4(b)、(c)所示。90°夹角试验方案中，次裂隙与主裂隙下半段关于试件中轴线对称分布，2条裂隙下部尖端裂纹扩展难易程度相当，试验中2条裂隙下端均产生了翼型拉裂隙并贯通至试件底部形成倒Y型分布，如图4(d)所示，导致试件最终破坏，此结果与文献[15]中所得结果基本一致。

通过上述4种方案可以看出，当交叉夹角为30°和60°时，主、次裂隙会形成1条组合裂隙。组合裂隙与两端产生的翼型拉裂隙形成贯通试件的破坏面，造成试件的破坏。夹角扩大到90°时，主次裂隙的下端都会产生翼型裂隙，且独立地沿轴向扩展。30°与60°夹角裂隙试件的主裂隙下部并无翼型裂隙产生，而是主裂隙上半段与整条次裂隙形成了组合裂隙逐步扩展，导致整个试件的破坏。

3 裂隙几何形式对强度影响分析

由图3可以看出，相交裂隙试件的峰值强度小于单一裂隙试件。这与文献[12]中的预制正交裂隙试件的单轴压缩试验研究结果相符，却与文献[7]中的交叉裂隙峰值强度略高于单一裂隙试件的试验结果相反，笔者认为这种现象的出现源于次裂隙是否贯穿主裂隙，从而导致裂隙试件的破坏形式不同。

根据线弹性断裂力学理论[16]，当正应力在垂直于裂隙面均匀分布时，会在裂隙两侧产生相互作用的剪切应力，这种剪切应力是促使岩体发生剪切破坏的主要驱动力。由于粗糙的闭合裂隙面产生摩擦现象，致使沿裂隙面发生剪切破坏的实际动力为该面上的有效剪力。根据材料力学，单轴压缩作用下含单一裂隙面的试件其裂隙破坏面上的正应力与剪应力可以表示为：

(1)

式中：σ，τ分别为垂直于裂隙的正应力与平行裂隙的剪应力，MPa；σ1为试件端部所施加正应力，MPa；α为裂隙与水平方向的夹角，(°)。

有效剪应力的计算公式为：

τ′=l(τ-σf)

(2)

式中：τ′为有效剪应力，MPa；l为裂隙长度，mm；f为裂隙面的摩擦因数。

将式(2)带入式(1)中可得：

τ′=σ1l[sin2α-f(1+cos2α)]

(3)

3.1 X型裂隙对试件强度影响分析

文献[9]中的裂隙形式X型裂隙，其裂隙形式如图5所示，主裂隙倾角更接近试件理论破坏角，更趋近于试件的破坏条件。裂纹沿主裂隙两端扩展，沿主裂隙方向产生的有效剪力最大，且2条裂隙(1条主裂隙，1条次裂隙，如图5所示)状态下，岩石峰值强度高于单一裂隙岩石，原因在于次裂隙的存在改变了主裂隙附近应力场，对主裂隙的扩展产生一定的抑制作用。为此，采用有限元法对该种预制裂隙方案进行分析，得到该试件在恒定应力下裂隙周围应力场的应力状态，如图6所示。

图5 X型裂隙示意Fig.5 X-type crack diagram

图6显示：最大剪切应力产生在主裂隙构成的贯通面上。将不同裂隙长度l、正应力σ带入式(2)中所得主裂隙贯通面上的有效剪力大于次裂隙面上的有效剪力，解释了其沿主裂隙方向扩展的起裂方式。图6中还可以观察到裂隙周围的应力方向。单裂隙试件的剪切应力平行于裂隙方向，而在X型交叉裂隙试件中由于次裂隙的存在，主次裂隙在交点两端都发生了应力方向的变化。次裂隙分担了主裂隙的正应力，主裂隙上交点两侧的剪应力方向发生了变化；方向相反的剪切应力部分抵消导致主裂隙滑动面上的有效剪力下降，最终导致试件强度较单一裂隙试件有所提高。

图6 X型裂隙试件剪切应力场Fig.6 X-type crack specimen shear stress field

3.2 近似T型裂隙对试件强度影响分析

4种方案下，主裂隙上半段裂隙扩展模式相似，故引起强度差异变化由下半段裂隙引起。单裂隙倾角对试件强度影响作用一般可以归为3类[17]：强度随角度增加而增加；强度随倾角先减小再增加；强度随倾角先增加后减小再增加。但当裂隙倾角大于45°时，强度都是随倾角的增加而增加。本试验中30°，60°，90°裂隙夹角所对应的次裂隙倾角分别为75°(与水平线右端夹角)，75°(与水平线左端夹角)，45°。30°与60°夹角所对应的次裂隙倾角相等，强度增加了49.4%，这是由于主裂隙上半段的应力方向的变化导致主次裂隙应力叠加与抵消作用。

图7为30°与60°夹角试件剪切应力方向图。结果显示：30°夹角试件中，主裂隙上半段剪切应力沿次裂隙方向的分应力与次裂隙方向相同，起到相互叠加的作用。60°试件则相反，起到抵消作用。抵消的剪切应力促使试件破坏需要更高的轴向应力，故60°夹角试件强度较30°试件有49.4%的提升。同为应力抵消作用的90°夹角试件，因角度增大导致分力减小，抵消作用减弱，强度应低于60°夹角试件。但由于实际单轴压缩过程中裂隙扩展结构效应的影响，主次裂隙下端都产生了贯通试件底端的裂隙。新裂隙的增加势必导致更多能量消耗，试件端部需施加更大的应力，在此作用下，90°夹角裂隙岩石较60°时，强度有所提升。