白砂糖电导灰分测定结果的不确定度评定

平秋婷，王桂华，张志强，余构彬，高裕峰

（1广东省生物工程研究所（广州甘蔗糖业研究所） 广东省甘蔗改良与生物炼制重点实验室，广东广州510316；2国家糖业质量监督检验中心，广东广州510316）

0 引言

制糖生产过程中，从原料到成品糖除含有蔗糖、还原糖外，还含有非糖物，非糖物中的无机成分对制糖过程及产品影响极大。因此，测定原料和成品糖中的灰分，掌握其变化规律，用以评价工艺条件的控制，改进生产管理，提高产品质量都具有重要意义[1]。电导灰分作为白砂糖分级评定的一项重要指标，其测量的准确性显得尤为重要[2]。本文依据新实施的国家标准GB/T 35887-2018《白砂糖试验方法》[3]，采用电导率仪法测定白砂糖的电导灰分，找出影响测定结果的不确定度的因素，通过建立数学模型对各个不确定度分量进行评估和合成，最终合成了相对标准不确定度和扩展不确定度。

1 材料与方法

1.1 实验仪器与设备

电子天平（精确至0.01 g），梅特勒-托利多（仪器）上海有限公司；DDSJ-308F电导率仪，上海仪电科学仪器股份有限公司；100 mL容量瓶（A级）。

1.2 实验试剂

去离子水，0.0025 mol/L氯化钾标准电导率溶液。

1.3 实验方法

称取白砂糖31.3 g±0.1 g于洁净烧杯中，加入去离子水溶解并移入100 mL容量瓶中，用去离子水多次冲洗烧杯及玻璃棒，洗水一并移入容量瓶中，加入去离子水至标线，摇匀。先用0.0025 mol/L氯化钾溶液校正电导率仪，用样液冲洗测定电导率用的电导电极及小烧杯2～3次，然后倒入样液，用电导率仪测定样液电导率，记录读数时的样液温度，计算结果。

2 数学模型的建立

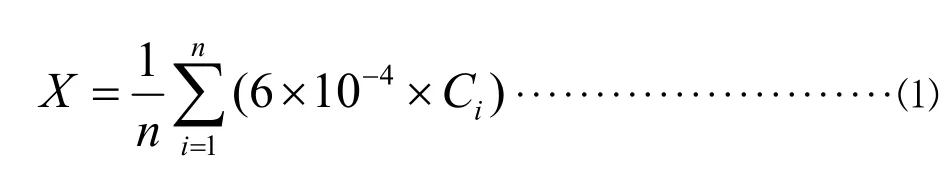
式中：X─电导灰分（g/kg）；Ci─313 g/L 糖液在20℃时经水溶液和温度校正后的电导率（μs/cm）；n─重复实验次数。

3 不确定度来源分析

测量不确定度是表征合理地赋予测量之值的分散性，与测量结果相联系的参数[4]。测量不确定度一般由若干分量组成，该分散性主要涉及A类不确定度、B类不确定度和合成标准不确定度：①A类不确定度：用对观测列进行统计分析的方法，用标准偏差表征，来评定标准不确定度；②B类不确定：用不同于对观测列进行统计分析的方法，也用标准偏差表征，来评定标准不确定度；③合成标准不确定度：当测量结果是由若干个其他量的值求得时，按其他各量的方差和协方差算得的标准不确定度[5]。

根据数学模型和测量过程，白砂糖电导灰分的不确定度来源包括（如图 1所示）：①样品质量引起的相对标准不确定度 urel（m），主要来源于电子天平的精度；②样品定容引入的相对标准不确定度urel（V），主要来源于容量瓶精度和环境温度；③重复测量引入的相对标准不确定度 urel（ci），主要由操作人员的操作水平高低决定；④电导率仪精度的相对标准不确定度urel（P），主要来源于电导率仪的精度。

4 不确定度分量评定

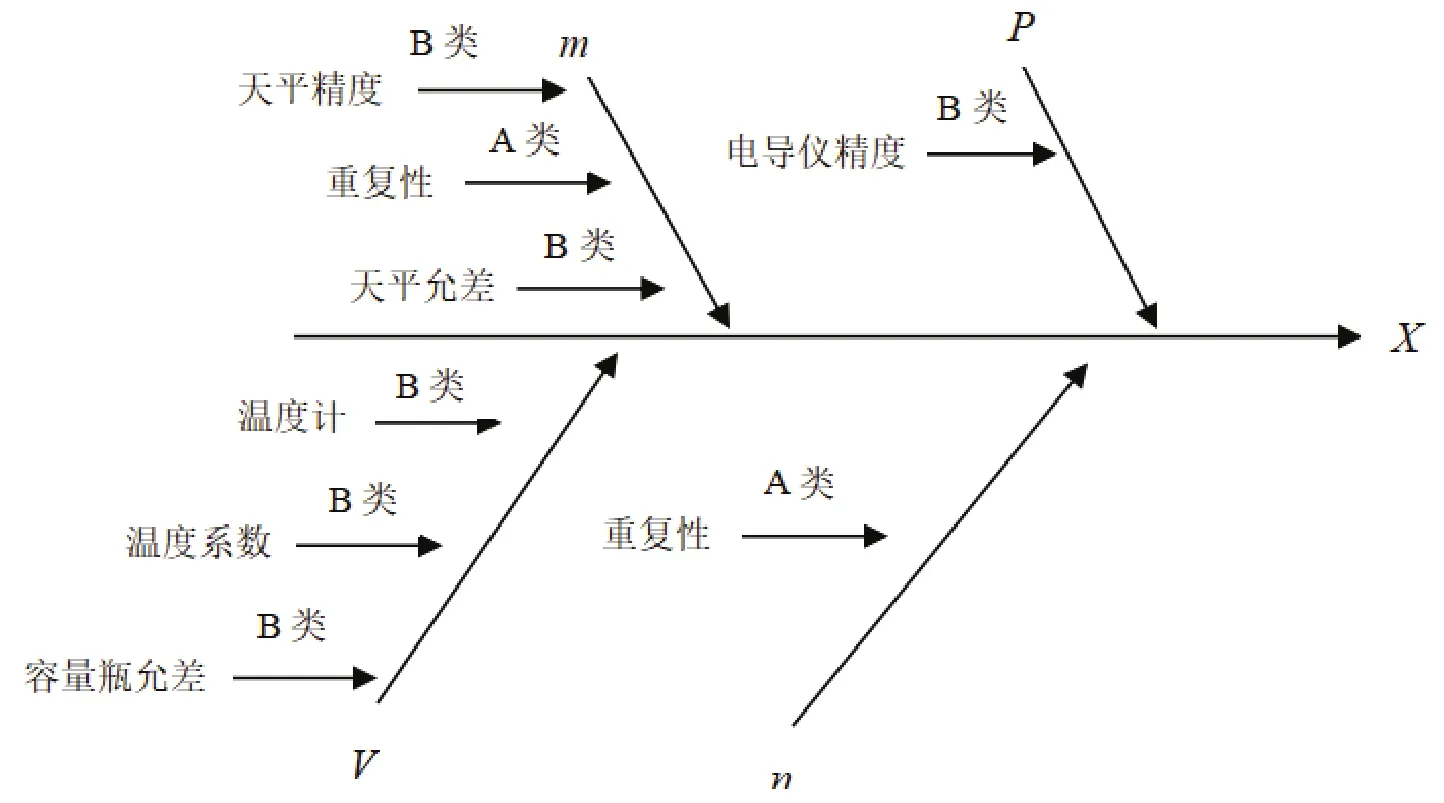
图1 白砂糖电导灰分的不确定度来源

4.1 样品质量引起的相对标准不确定度urel（m）

质量m不确定度来自3个方面：第一，称量的重复性，可以通过10次重复测量，采用 A类评定方法求出；第二，由天平称量不准引入的不确定度，按B类方法评定；第三，天平标度的可读性（数字分辨力），按B类方法评定。

4.1.1 重复性引入的标准不确定度分量uA（m）

对质量m进行重复10次的测量，测量结果见表1。采用贝塞尔公式计算标准不确定度uA（m）为：

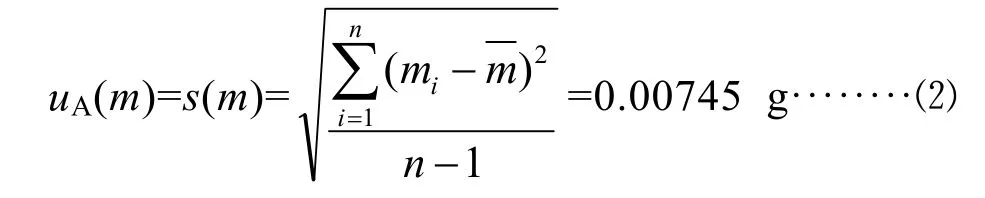
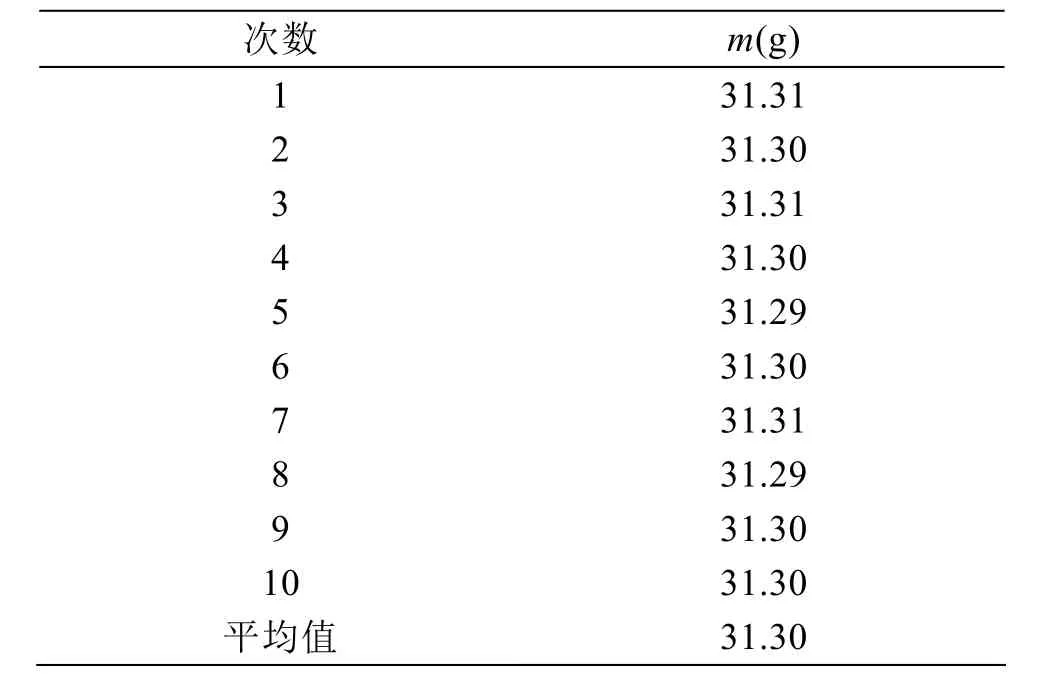
表1 样品质量10次重复测量结果

4.1.2 天平允差引入的标准不确定度分量uB1（m）

电子天平的最大允差为±0.1 g，则区间半宽度a1（m）=0.1 g，假设m测量值落在该区间的概率分布为均匀分布，包含因子k1（m）=3，因此标准不确定度为：

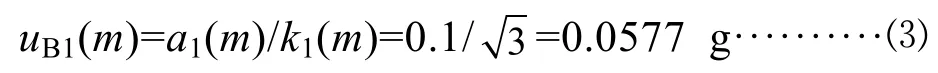
4.1.3 天平分辨力引入的标准不确定度分量uB2（m）

数字式测量仪器对示值量化（分辨力）导致的不确定度服从均匀分布。天平分辨力为 0.01 g，区间半宽度 a2（m）=0.01 g，包含因子 k2（m）=因此标准不确定度为：

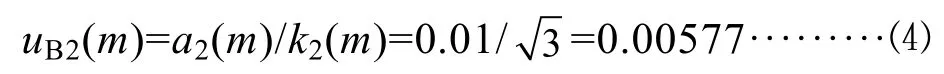
4.1.4 质量m的合成标准不确定度uc（m）和相对标准确定度 urel（m）

上述3个分量相互独立，互不相关。因此合成标准不确定度为：

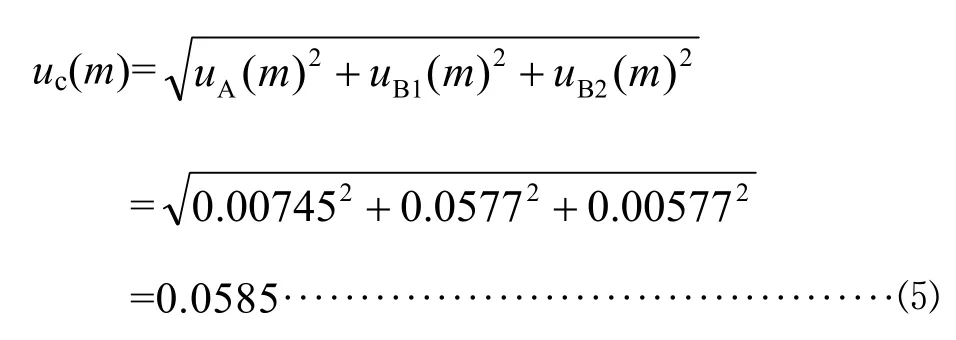
其相对标准不确定度为：

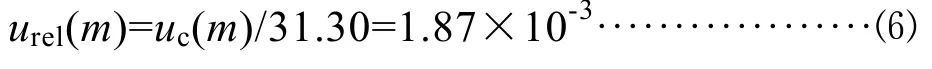
4.2 样品定容引入的相对标准不确定度urel（V）

样品定容引入的不确定主要来源于2个方面：最大允差和温度影响，两者均按B类方法进行评定。

4.2.1 容量瓶允差引入的标准不确定度分量uB1（V）

A级100 mL容量瓶的允差为±0.1 mL[6]，则区间半宽度 a1（V）=0.1 mL。在没有给出置信水平或分布的情况下，假设其服从三角分布，则包含因子

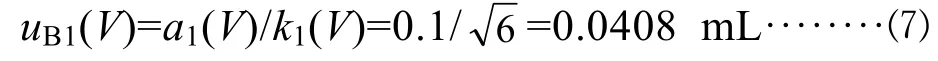
4.2.2 温度系数引入的标准不确定度分量uB2（V）

容量瓶的检定或校准一般是在室温20.0℃环境条件下进行的[3]，本研究在 25.0℃条件下进行。水的体积膨胀系数为2.1×10-4/℃，产生的体积变化为±（100×5×2.1×10-4）=±0.105 mL，将其设为均匀分布，其标准不确定度为：

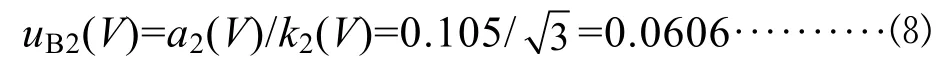
4.2.3 玻璃温度计校准引入的标准不确定度分量uB（t）

根据玻璃温度计校准证书上显示的温度最大允差为±0.20℃，则区间半宽度 a（t）=0.20℃，在 95%的置信区间中，假设其服从均匀分布，则包含因子因此其标准不确定度为：

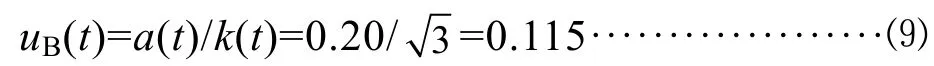
4.2.4 样品定容引入的合成标准不确定度 uc（V）和相对标准不确定 urel（V）因此其标准不确定度为：

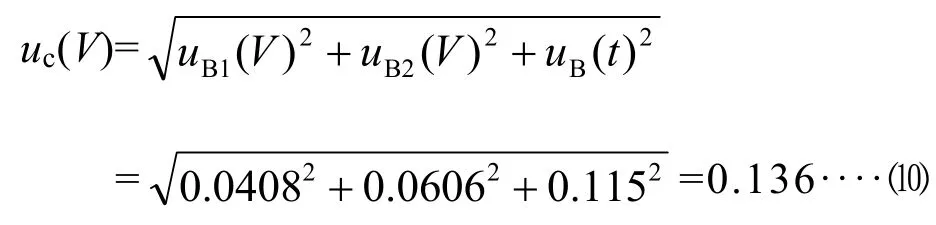
其相对标准不确定为：

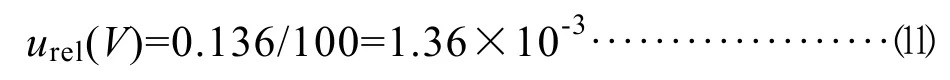
4.3 重复测量引入的相对标准不确定度urel（ci）

对同一白砂糖样品重复测定10次，结果见表2。

采用贝塞尔公式计算，求得单次测量标准差s（ci）为：

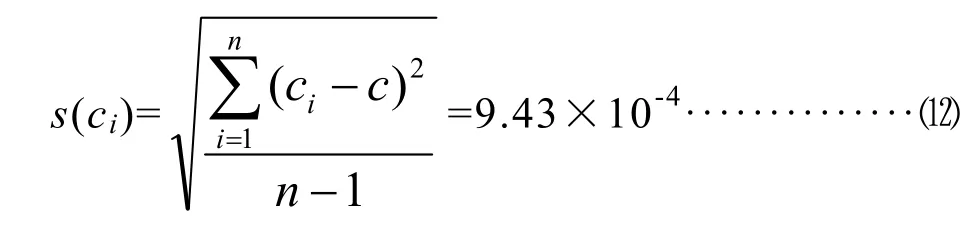
由测量重复性导致的标准不确定度u（c）为：

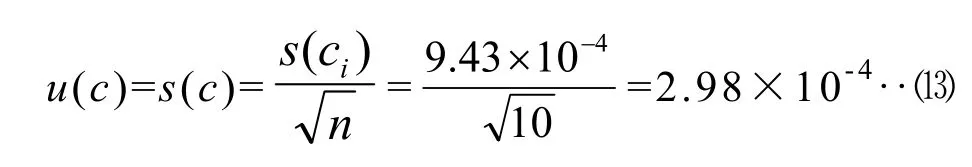
因此，重复测定的相对标准不确定度为：

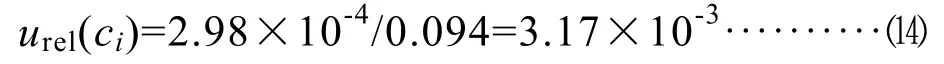
4.4 电导率仪精度的相对标准不确定度urel（P）

仪器检定证书给出仪器的总体扩展不确定度U（P）=0.3%，则区间半宽度为 a（P）=U（P）=0.3%；样品的电导灰分在20℃测量平均读数为16.00 μs/cm，服从正态分布，在置信区间 95%，则包含因子k（P）=2，其相对标准不确定为：

表2 白砂糖样品电导灰分测定结果

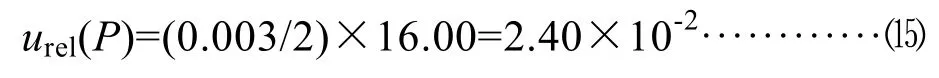
4.5 计算合成相对标准不确定urel

各个不确定度分量计算值如表3所示。

合成相对标准不确定为：

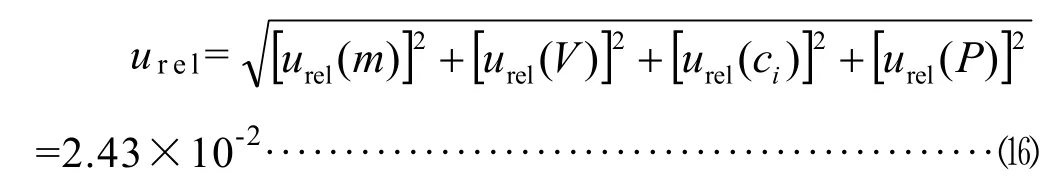
4.6 扩展不确定U

表3 白砂糖电导灰分测定相对不确定分量评定结果

由表1可知，白砂糖样品的电导灰分平均值为0.094 g/kg，其合成标准不确定度为 u=2.43×10-2×0.094×100%=0.23%，在95%置信水平下，包含因子取k=2，扩展不确定为：U=ku=0.46%，实际白砂糖样品的电导灰分测定结果可表示为：0.094±0.0046 g/kg。

5 结论

采用电导率仪法测定白砂糖电导灰分的过程中，影响测定的不确定度主要来源于样品质量、样品定容体积、重复测量和电导率仪精度4个方面引入的不确定度分量。在现有实验条件下，测定结果的标准不确定度为 0.23%，在 95%置信水平下，扩展不确定为：U=0.46%，实际白砂糖样品的电导灰分测定结果可表示为：0.094±0.0046 g/kg，满足白砂糖电导灰分检测的标准要求。