内支线配船与船舶调度优化

郑红星， 李珊珊， 司 羽

(1. 大连海事大学 交通运输管理学院，辽宁 大连 116026; 2. 天津外轮代理有限公司,天津 300456)

0 引 言

支线运输作为干线运输的货源保障，其地位日益提升[1]。但由于内支线集装箱运输市场货源不稳定，如何通过合理调配内支线船舶来降低营运成本，同时考虑客户满意度，是当前从事内支线运输的航运企业亟待解决的关键问题。

目前，国内外有关航线配船和船舶调度的研究主要集中在干线运输方面。G. BRONOM等[2]针对不定期运输企业的航线设计、航线配船与货载选择等问题，构建了整数规划模型，并用集分隔方法求解；M. CHRISTIANSEN等将VRPPD理论运用到干线散货船舶调度问题中，构建了集送货一体的多船型船舶调度模型[3-4]；C. HSU等[5]研究了轴辐式航线网络设计问题，构建了以营运成本和库存成本最小为目标的数学模型，得到最佳的船舶航线以及每条航线配置的船型和发班间隔；徐骅等[6]研究了竞争市场中集装箱班轮航线优化问题，集成考虑了运力闲置与多航线配船问题。在支线运输方面，靳志宏等[7]研究了支线船舶调度问题，用软时间窗约束保证箱位利用率，构建了以航行成本最低为目标的数学模型；杨立乾等[8]基于轴辐式航线，构建了支线运输多船型船舶调度模型，论文中假设各喂给港可被不同船舶挂靠多次，这点和本文问题相似；靳志宏等[9]针对集装箱支线运输船舶调度问题，提出了航次串的概念，把航次配船转化为对“航次串”配船；计明军等[10]以干线船舶限制时间和支线船舶容量为基础，建立了集装箱船舶支线运输的航线优化模型，并应用于珠三角支线运输中；庞玺斌等[11]针对单航次单喂给港的运输方式，以船队总运输成本最小为目标，构建了整数规划模型，模型中一条船可以承担多条航线的运输任务，该模型可以同时解决航线选择、航线配船、船队组建问题。

综上，目前对航线配船和船舶调度的研究主要以干线班轮运输为主，少量文献对支线班轮运输进行研究，且多以运输成本或运输时间为单一目标，罕有研究支线不定期船舶运输。而在不定期的内支线配船和船舶调度中，不仅需要考虑枢纽港的船舶限制时间，还需考虑船舶甩货成本，值得深入研究。

区别已有文献，考虑计划期内各港口不同时段的货运需求，以内支线船舶的营运成本和甩货成本之和为优化目标，兼顾船舶在调度中可能出现的主动滞港情况，将内支线配船和船舶调度集成为一体，求得计划期内配置船舶的最佳类型和数量，以及每艘船舶的最优调度方案。

1 问题描述

研究一个枢纽港和众多支线港之间的集装箱运输问题，内支线船舶需将支线港货物在限定时限内运至枢纽港，然后由干线班轮运达目的地。在计划期期初，依据本计划期内枢纽港班轮船期和各支线港的货运量，从事内支线运输的航运企业要明确该计划期内配置船舶类型、数量和支线港的挂靠次序。

为协调内支线营运成本与客户服务水平的矛盾，文中引入了甩货成本、船舶调度最小耗时和主动滞港的概念。其中，在某计划期内，航运企业出于营运成本的考虑，导致部分集装箱未能赶上计划期内的干线班轮，由此造成班轮箱位利用率降低以及客户满意度下降带来的损失称为甩货成本；船舶调度最小耗时是指船舶由枢纽港出发经过各支线港口最终回到枢纽港所花费的航行时间，进而得到计划期内每艘船舶的最大调度次数；主动滞港是指船舶为充分发挥其作业效能，提高舱位利用率，而采取的在港外停泊若干小时再进港作业的策略。

2 优化模型

2.1 假设条件

1)船舶从枢纽港出发至返回枢纽港为一次调度，船舶每次调度经过的支线港不能重复，不考虑支线港之间的运输业务；

2)同一支线港在计划期内可被多次挂靠，并假设船舶航速相同；

3)计划期按小时分为若干时段；

4)取3 h为船舶停泊(滞港)时间最小单位，即1、2、3表示滞港时间为0 h、3 h和6 h等；

5)船舶在港作业时间已知；

6)各支线港的集装箱根据要赶上的班轮不同进行分类。

2.2 符号定义

2.2.1 参数说明

2.2.2 中间变量

2.2.3 决策变量

Xvkij为0～1变量，若船舶v在第k次调度中，由港口i行驶到港口j，则为1，否则为0；Wvki为船舶v在第k次调度中，在港口i的滞港时间；Yvki为0～1变量，若船舶v在第k次调度中，在港口i挂靠，则为1，否则为0；Zv为0～1变量，若船舶v在计划期内投入使用，则为1，否则为0。

2.3 模型建立

在计划期内，总成本由两大部分组成，第一部分为内支线营运成本，包括船舶配置成本Z1、船舶在各港口间的总运输成本Z2、船舶在各港口的总停泊成本Z3以及支线港集装箱处理成本Z4；第二部分为内支线配船与船舶调度后的甩货成本Z5。以上述成本之和最小为目标，建立了如下数学模型。

目标函数:

MinZ=Z1+Z2+Z3+Z4+Z5

(1)

(2)

(3)

(4)

(5)

约束条件：

(6)

(7)

(8)

Yvkm=1,v∈V,k∈K

(9)

(10)

(11)

v∈V,k∈K,i,j∈W

(12)

(13)

(14)

(15)

(16)

(17)

(18)

t≤Avki+BvkiM

(19)

t≥Avki-(1-Bvki)M

(20)

(21)

式(1)～式(4)表示内支线营运成本；式(5)表示甩货成本，为班轮到达枢纽港前各港口的总货运需求量与限制时间内运输量之差乘以单位缺货成本；式(6)、式(7)船舶在每次调度中，由枢纽港出发最后回到枢纽港；式(8)计划期内每个港口至少被挂靠一次；式(9)表示船舶在每次调度中必须挂靠枢纽港；式(10)表示船舶驶入某支线港就必须从该港驶出；式(11)保证船舶每次调度中航行时间的连续性；式(12)表示上次调度中到达枢纽港的时间与下次调度到达各港口时间的关系；式(13)、式(14)表示船舶每次调度中在各港口装载量的约束；式(15)表示船舶在每次调度中，总装载量不得超过船舶容量；式(16)表示船舶每次调度中，抵达各港口时船舶的剩余容量；式(17)表示在每次调度中，船舶在某港口的装货量不大于其到达该港时的剩余容量；式(18)～式(20)表示各港口在不同时段的剩余货量；式(21)表示各支线港的不同集装箱送达枢纽港的时间限制，即如果船舶在某次调度中在某个港口装载了d类集装箱，则该船舶返回枢纽港的时间不得超过d班轮的限制时间。

2.4 求 解

笔者研究问题属于NP-Hard问题，基于模型特点设计了和声退火混合算法。该算法在模拟退火算法中嵌入和声搜索算法的和声记忆库，并结合问题特点，基于启发式规则初始化和声记忆库。算法步骤如图1。其中HMCR为记忆库保留概率，HMS为和声记忆库中的和声数。

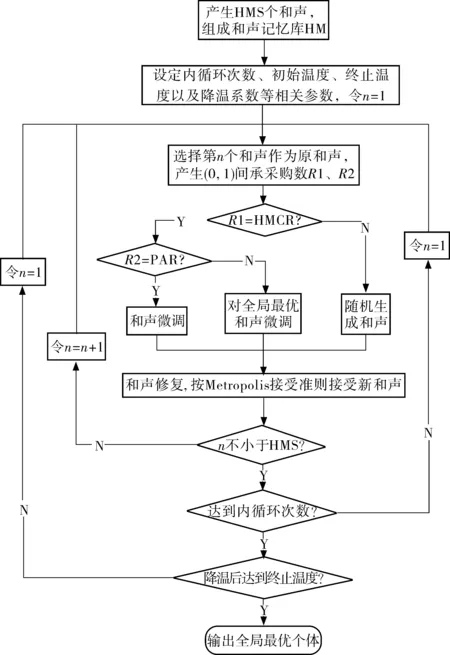
图1 算法流程Fig. 1 Algorithm flowchart

2.4.1 解的表示及编码

对于m个港口、n艘船舶、最大调度次数为G的内支线配船与船舶调度问题，用1×[n×(G×m+1)]的一维行向量来表示和声个体。具体解的表示如图2。1到m列表示船舶1第1次调度方案，m+1到2×m列表示船舶1第2次调度方案，以此类推，其中0代表不挂靠对应的港口，1代表挂靠对应的港口，2代表挂靠对应的港口且主动滞港3 h后进港，3代表挂靠对应的港口且主动滞港6 h后进港，以此类推；第n×G×m+1列到n×(G×m+1)列表示船舶是否投入使用，1代表使用，0代表不使用。此外，由问题特点可知枢纽港m的值必为1。

图2 解的表示图Fig. 2 The representation graph of the solution

2.4.2 初始和声记忆库的生成

为有效提高算法的搜索性能，考虑各港口集装箱货运需求量对船舶调配方案的影响，设计了基于问题特点的记忆库生成策略，具体如下。

Step1：初始化算法参数及和声记忆库，输入相关数据，令和声数p=1，和声列数i=1；

Step2：计算各港口在不同时段对集装箱货运需求量的总和，记为行向量HCL，转至Step3；

Step3：计算HCL中的最大值，即为maxHCL，将HCL中各元素分别除以maxHCL，记为新行向量NHCL，转至Step4；

Step4：若第i列对应的是港口序号，则转至Step5；否则，转至Step7；

Step5：若第i列对应的是枢纽港(港口m)，则第p个和声个体第i列的取值为1；否则，转至Step 6；

Step6：结合行向量NHCL确定第p个和声个体第i列的取值，按行向量NHCL中取值的大小接受，转至Step8；

Step7：随机生成第p个和声个体第i列的取值(0或1)，转至Step8；

Step 8：若小于n×(G×m+1)，则令j=j+1，转至Step4；否则，转至Step9；

Step9：若p小于HMS，则令p=p+1，转至Step4；否则，输出初始和声记忆库HM。

2.4.3 新和声产生策略

采用3种策略生成新和声，分别为和声微调、对全局最优和声微调以及随机生成和声。其中，和声微调策略包括两种，第1种是随机选择某局部片段进行+1或-1处理，如图3，第2种是将全局最优和声的某片段嫁接至当前和声个体中，如图4，且这两种策略的选择受到参数全局优化率的影响，取值在0.5与0.8之间；对全局最优和声微调同和声微调1类似；随机生成和声同2.4.2节中的步骤类似。

图3 和声微调1Fig. 3 Harmonic fine-tuning 1

图4 和声微调2Fig. 4 Harmonic fine-tuning 2

2.4.4 和声修复策略

不可行和声的出现，主要有以下3种情况：① 前G×m×n列中枢纽港对应的元素值不为1，其余港对应的元素值小于0，以及最后n列的元素值超出[0,1]区间；② 各船舶未能按照第1次调度、第2次调度、第3次调度的顺序进行调度；③ 船舶进行调度，而对应的船舶是否投入使用列为0，或者船舶未投入使用，却进行船舶调度。针对这些问题，设计了以下和声修复策略。

1)依次检查所有列，若对应的为枢纽港序号，将取值不为1的列修复为1；若对应的为非枢纽港和非船舶是否投入使用列，将小于0的列修复为0；其余列取值若不在[0,1]区间，则随机生成为0或1。

2)依次检查所有列，对于某艘船舶，若第1次调度对应的列(除枢纽港)为0，则其余取值为0；否则检查第2次调度对应的列，如果除枢纽港外，取值为0，则后面所有港口列取值为0,对应的船舶是否投入使用列取值为1。

2.4.5 相关约束处理

2.4.6 算法终止条件

以算法的迭代温度达到终止温度作为终止条件。

3 算例分析

3.1 算例描述

经营渤海内支线集装箱运输的S企业拥有7条支线船舶，负责班轮船舶A和B的集装箱收集工作，将集装箱由7个支线港向大连港集运。其中，班轮船舶A每周五上午4点到达大连港，船舶B每周日上午6点到达大连港，计划开始时间为周一0点，计划期为一周(24×7)h，A班轮集装箱送往枢纽港的限制时间最迟为第100时，B班轮集装箱送往枢纽港的限制时间最迟为第150时。

结合港口的地理位置分布，规定大连港为枢纽港，标号为8，各支线港标号为1～7，将港间运输距离转化为运输时间，见表1。结合港口间运输时间，可以确定船舶调度最小耗时为49 h，因此假设各船舶计划期内最大调度次数为3次；由于存在甩货情况，因此计划期初在各港口有上计划期未运输的集装箱，各支线港口期初和本计划期总运输需求量见表2；各支线船舶资料具体见表3。

表1 港间运输时间Table 1 Transport time between any two ports h

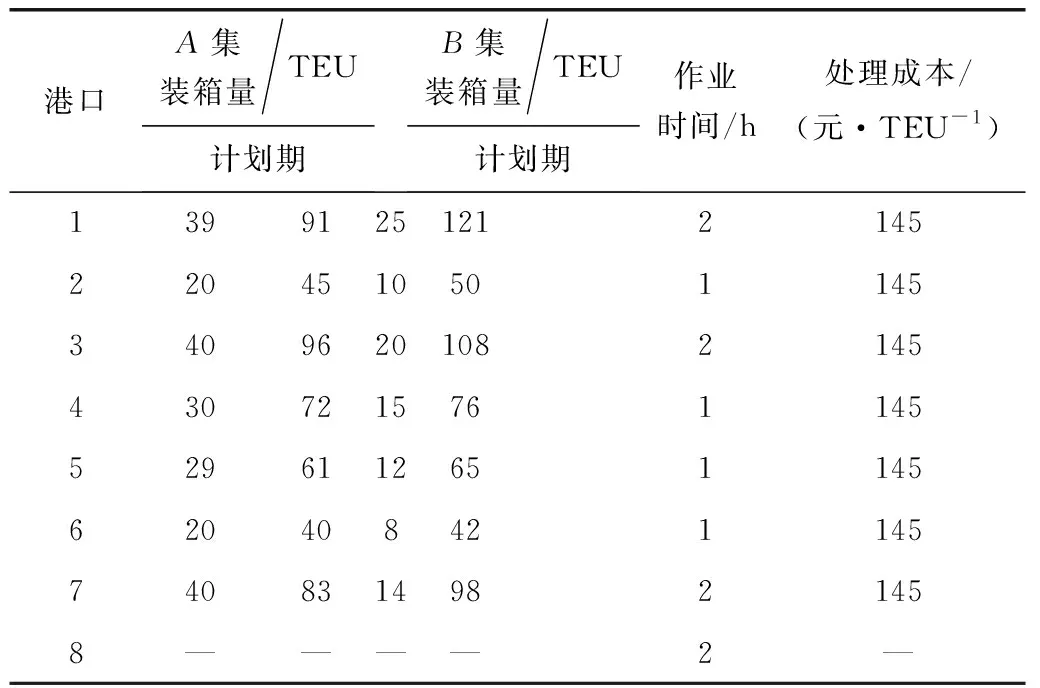
表2 各港口货运需求量、作业时间和集装箱处理成本Table 2 Freight demand, operation time and container handling cost of each port

表3 船舶相关信息Table 3 Ship related information

设定算法参数为：和声记忆库大小30，初始温度100 ℃，终止温度1 ℃，降温系数0.95，内循环迭代次数15，记忆库概率0.95，和声微调概率1(温度30以上)、0.5(温度30以下)，全局优化率0.7。

3.2 方案有效性检验

根据调研，经营渤海内支线集装箱运输的公司主要有两种不定期船舶调度方案，方案1为支线船沿着8-1-2-3-4-5-6-7-8顺次挂靠，不可跳跃，船舶最大限度装载，不考虑滞港情况；方案2为支线船舶结合港口不同时段的货运需求进行跳跃挂靠，每次调度中最大限度装载，不考虑滞港情况。对于方案1，由于其为不可跳跃挂靠，会出现当港口货量很少也必须挂靠，造成时间的消耗和运输成本的大幅增加，使总成本较高，因此笔者主要与方案2进行对比。

考虑6种规模的货量，分别为原始数据的0.8倍、1倍、1.2倍、1.4倍、1.6倍和1.8倍。其中计划期内各港口各时段的货运需求量结合各港口的周需求量随机产生，得到如表4的方案对比结果。

表4 方案结果对比Table 4 Comparison of different scheduling results

注：优化率=(现实方案-本文方案)/现实方案服务率=限制时间内的运输总量/班轮到达枢纽港前货运需求量

由表4可知，在不同规模下，方案同现实方案的目标值平均相对优化率为18.54%,方案的服务率也高于现实方案。这是由于班轮船期不同，当采取最大限度装载时，会使得不满足班轮船期要求的集装箱占用了部分船舶容量，例如船舶到达某港口的时间超过较近班轮的船期，而根据装载原则，却可能装载该类集装箱，从而使本计划期的服务率降低，造成较高的成本，而装载时优先满足本次计划期内两艘班轮的需求，在此基础上，如还有剩余容量才可能装载下计划期班轮的集装箱，使得本计划期服务率较高。且考虑滞港情况，使支线船舶得到充分利用。

以原始数据为例进行试验，阐述依据模型和算法得出的优化方案。利用和声退火混合算法求解得总成本收敛结果见图5，此时的总成本为488 330元，耗时28.544 405 s。配置船舶1、船舶3，调度方案为，船舶1：000001111111000101011101，船舶2:

101121011010022111321221。以船舶1的为例，调度方案如图6。

图5 最优方案收敛Fig. 5 Optimal scheme convergence graph

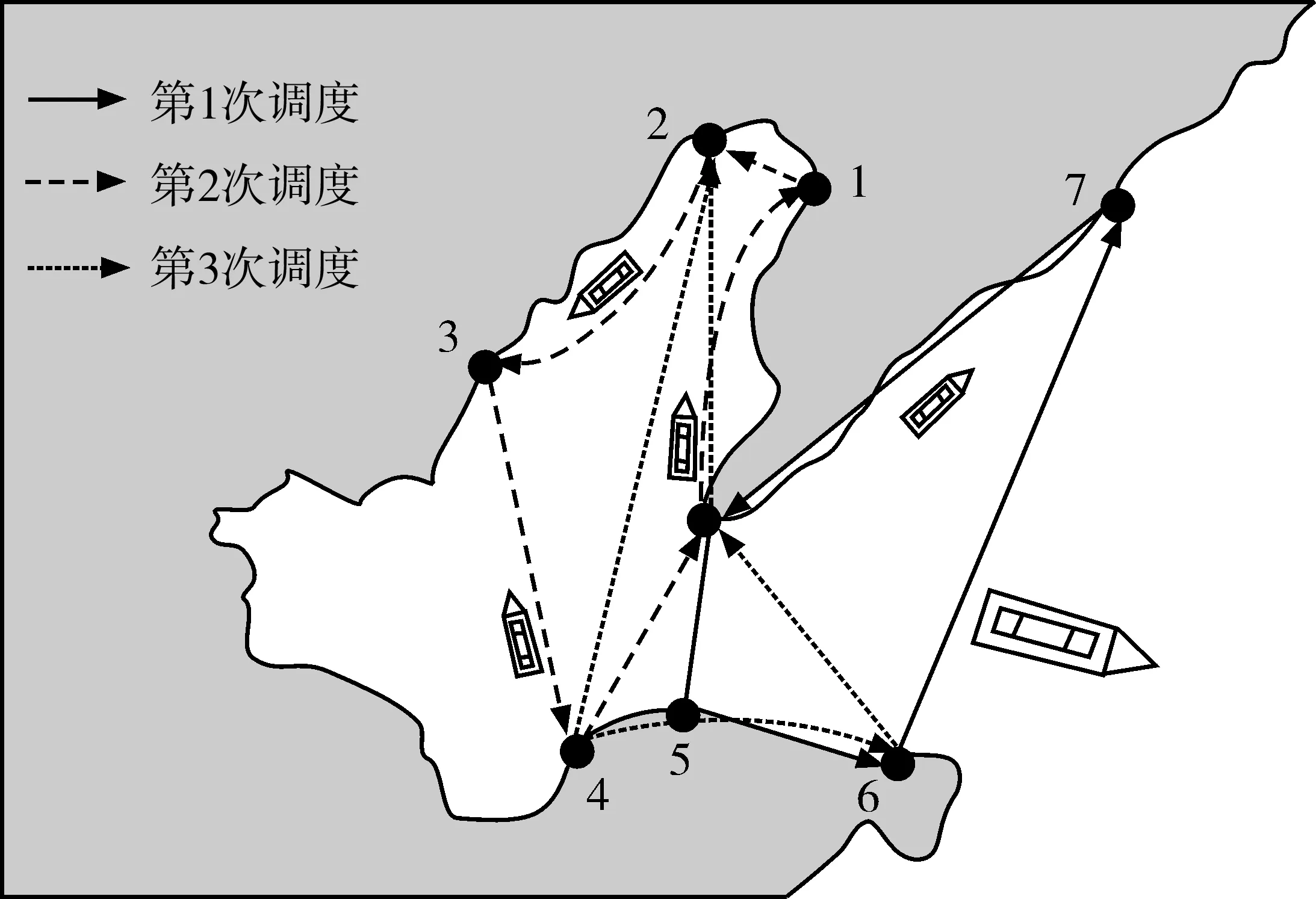
图6 船舶1调度方案示意Fig. 6 Ship 1 scheduling plan

4 敏感性分析

4.1 枢纽港船舶限制时间灵敏度分析

枢纽港船舶限制时间(即集装箱送达枢纽港的限制时间)的变化会对总成本和服务率产生影响，为分析其影响，将限制时间分为5种情况，分别为T1、T2、T3、T4、T5，取值为原限制时间减20、减10、不变、加10、加18(计划期为168 h，限制时间不超过计划期)。不同限制时间下的总成本和服务率如图7、图8。

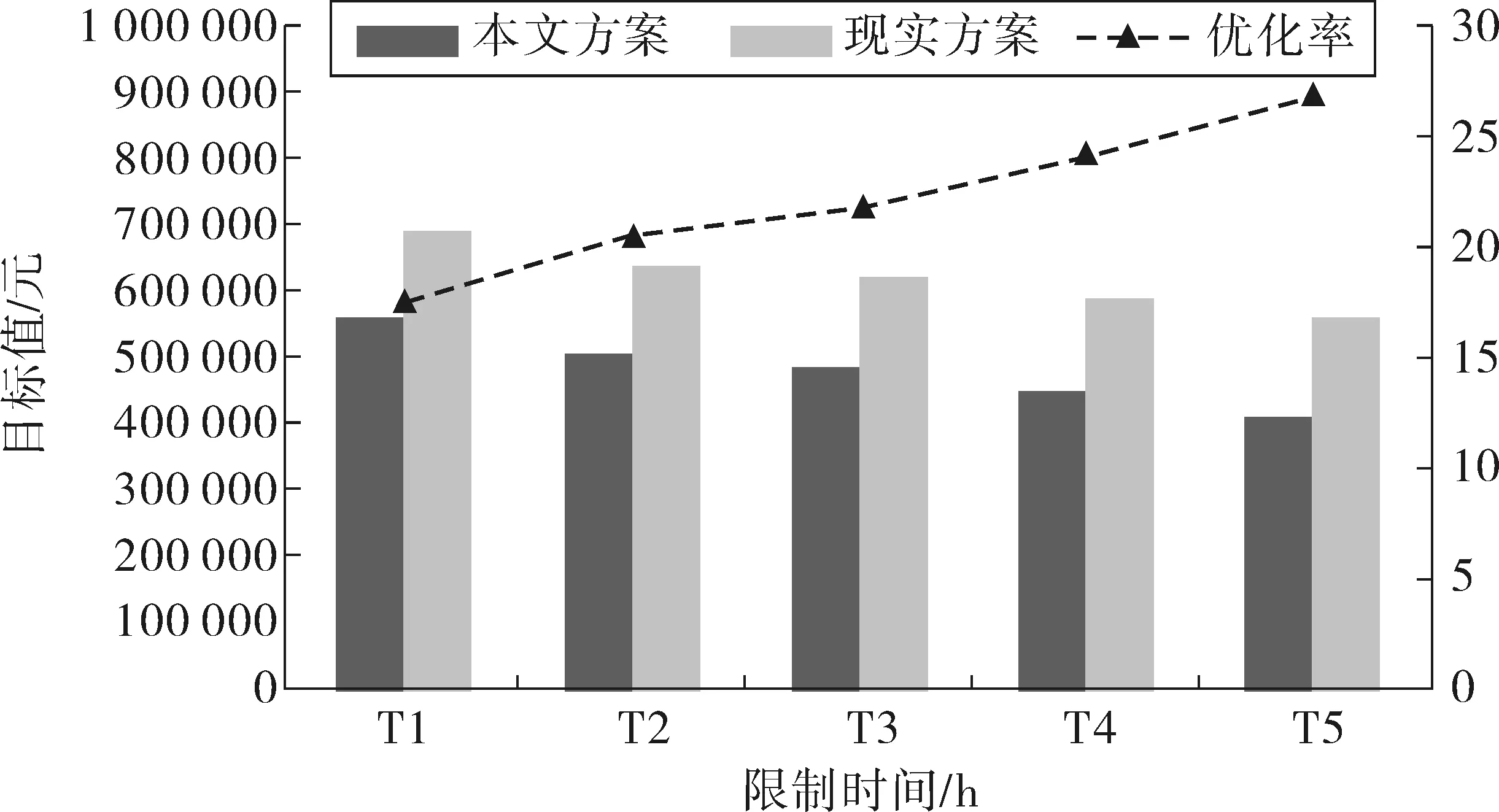
图7 限制时间对成本的影响Fig. 7 Total cost under different time constraints

图8 不同限制时间对服务率的影响Fig. 8 Service rate under different time constraints

可以看出，限制时间的放大，两种方案的目标值都在降低，优化率上升，服务率增加。这是因为当限制时间放大后，限制时间内到达各港口的集装箱总量增加，同时支线船舶有更充足的时间进行调度，使得服务率提高；随着服务率的增加，总营运成本降低，可视为集装箱运输量的增加带来甩货成本的减少量大于运输成本和集装箱处理成本的增加量，且不同限制时间下本文方案成本下降的比例大于现实方案，优化率呈上升趋势。

4.2 单位甩货成本灵敏度分析

甩货成本是由于干线班轮箱位利用率降低和客户满意度下降所造成的损失，客户对企业的重要性以及企业对客户服务水平的重视程度均会对单位甩货成本造成影响。为了分析其影响，取初始数据的1倍、1.5倍、2倍、2.5倍进行试验。不同单位甩货成本下方案对比如图9、图10。

图9 甩货成本对总成本的影响Fig. 9 Total cost under different rejection costs

图10 单位甩货成本对服务率的影响Fig. 10 Service rate under different rejection costs

可以看出，随着单位甩货成本的增加，两种方案的目标值和服务率均增加。这是由于随着单位甩货成本的增加，甩货成本对总成本的影响增大，从而运输更多的集装箱；但现实方案的服务率水平较低，所以随着单位甩货成本的增加，总成本增加较大，使得本文方案相对现实方案的优化率不断提升；本文方案中随着单位甩货成本的增加，总成本小幅度增加，但获得了服务率的提升。这表明航运企业在制定船舶调度方案时应在总成本和服务率之间寻求平衡，给出整体最优的决策。

5 结 论

1)建立了基于不定期船舶的内支线配船与船舶调度模型，在枢纽港班轮船期和计划期内各港口不同时段货运需求已知的前提下，考虑营运成本和甩货成本，有利于平衡营运成本和服务水平，提高企业的整体运营绩效。

2)设计了和声退火混合算法，包括初始记忆库的生成、新和声的产生以及和声修复，有效提升了算法的搜索性能。

3)敏感性分析实验表明，枢纽港船舶限制时间对总成本和服务率的影响较大，随着限制时间的放大，总成本降低，服务率提高；单位甩货成本的变化对总成本和服务率也会产生影响，随着单位甩货成本的增大，本文方案的总成本小幅度增加，服务率上升，相对现实方案的优化效果越明显。因此，航运企业应尽量放大限制时间，同时关注单位甩货成本，做出有利于整体的最优决策。

未来的研究可考虑多枢纽港、集送货一体以及各港口集装箱到达规律可变等因素，使该问题的研究更符合现实需求。