施工环境下高速公路应急资源调度方法研究

王 薇， 武 毅， 赵 阳， 瞿卫东

(1.吉林大学 交通学院，吉林 长春 130022；2. 吉林省道路交通重点实验室，吉林 长春 130022)

0 引 言

近年来，我国高速公路快速发展，路网骨架已基本形成。在完善高速公路路网建设的同时，应该注重高速公路的运营及管理。目前国内外均缺乏对于施工环境下高速公路应急车辆资源配置的研究，高速公路施工区域的应急车辆配置基本都根据高速公路管理部门或工程人员的经验，缺乏科学性，尤其是施工环境下的应急资源调度技术基本处于空白。据相关资料统计，我国已有约60%的高速公路路段建立了应急救援系统，但是大部分的救援系统都属于建设初期阶段，在信息联动方面及优化资源调度上考虑较少。由于高速公路采取全封闭设置，车辆行驶速度较高，发生事故易造成较严重后果。例如2012年广深高速上发生一起油罐车与货车追尾碰撞事故，油罐车漏油起火，由于道路封闭导致救援不及时，致使20人死亡15人受重伤[1]。因此考虑高速公路施工区域的性质和特点，以最佳救援效率为目标，建立了基于施工区通行能力与历史事故数据的应急资源配置模型。

国内外专家针对高速公路应急资源调度均做了大量研究。在国外，F.WEX等主要研究了如何利用智能决策理论和计算机辅助工具制定可行的应急救援物资分配和调度方案, 使得各储备点的救援物资能够及时合理的运送到各发放点[2]；I.SUNG等针对单一应急资源，考虑在资源有限的情况下如何分配使救助人数达到最大化，涉及了资源的分配和路径规划[3]。虽然上述研究开始考虑多个物资发放点的情况，但是仍局限于单种救援物资的应急请求。C.LIU等基于Petri网对考虑应急资源约束和不确定周期的应急响应过程进行建模和分析[4]。

在国内，石志刚等研究了不同阶段高速公路交通事故紧急救援过程中所需要的不同资源，根据资源类别的不同建立了以区域配置数量最小值的应急资源调度模型[5]；黄德启在研究区域路网算法和模型的基础上，研究了紧急资源优化配置策略，根据不同交通事故风险评价结果对救援目标进行排序，并给出了对应的应急资源配置算法[6]；柴干等基于高速公路事故发生的随机性，研究了交通应急救援资源随机模型，确定了救援服务水平、事故概率的权重并通过研究模型的求解、配置和参数选择建立了完整的紧急资源配置方案[7]。王旭坪等构建了以最小化公众心理风险感知程度和物资未满足度为目标的混合整数规划模型, 并设计了基于分枝定界的多层搜索算法[8]。

通过以往的研究可以发现，事故后及时的救援可以大大减少人员及财产损失。我国交通事故中有60%是因为重伤员未及时、有效得到救护而死亡，只有15%的伤员是乘坐救护车就医。而对于重伤者，30分钟内得到救治，生存率可达80%；60分钟内得到救治，生存率可达40%；而90分钟内得到救治的伤员生存率只有10%以下。

出救点如何选择一条能够第一时间到达救援现场的路线就显得尤为重要。由于车辆在经过施工区时，施工区环境混乱，可供行驶道路减少导致行驶相对缓慢，道路通行能力显著降低，因此应该针对高速公路施工区不同的施工形式给出相对应的、合理的应急资源调度方案。笔者结合高速公路特征及高速公路施工区不同交通组织对高速公路施工区通行能力进行了深入的研究，在此基础上提出了基于高速公路施工区通行能力的应急资源调度模型。研究对于交通事故中如何降低人员伤亡及财产损失具有重要的理论价值和实际意义。

1 施工区通行能力分析

道路路段基本通行能力也称理论通行能力，是指在理想的道路、交通、控制和环境条件下，不考虑服务水平，在单位时间通过一条车道或某一车行道上某一断面的最大车辆数，它是路段所能承受的交通负荷极限[9]。

由于高速公路施工环境较为复杂，施工区路段的交通条件与正常路段有明显区别，高速公路施工区的通行能力可以有效地对该段区域的交通运行状态进行描述。影响其通行能力的因素很多，通常需要借助现场观测和交通仿真软件对施工区的通行能力进行研究。

1.1 影响因素及量化

通过施工路段封闭形式、车道宽度、路侧净宽、施工车道数、驾驶员路段熟悉程度等对基本通行能力进行了修正，并依据修正后的通行能力建立了应急资源调度模型。

在高速公路基本通行能力Cb的基础上，定义了车道施工修正系数fr、施工区车辆构成系数fC、路段熟悉度修正系数fp和施工区单向可行驶车道数n并进行了量化。

1.1.1 高速公路施工区通行能力

高速公路施工区域单向通行能力可以按照下式计算：

C=Cb×fr×fC×fp×n

(1)

式中：C为施工区域通行能力,pcu/h；Cb为高速公路基本通行能力,pcu/h；fr为车道施工修正系数；fC为施工区车辆构成系数；fp为路段熟悉度修正系数；n为施工区单向可行驶车道数。

1)高速公路基本通行能力Cb。

表1给出了理论下高速公路不同设计速度下每车道的基本通行能力值[10]。

表1 高速公路基本通行能力Table 1 Basic traffic capacity of highway

(2)

2)车道施工修正系数fr。

车道施工修正系数是根据施工区高速公路实际车道宽度、施工预留的路侧净空、高速公路可供行驶的车道数、以及路侧是否有障碍物而得到的。

如果两侧障碍物距离到中央分隔带的距离不相等，取两侧距离的平均值。具体系数如表2[10]。

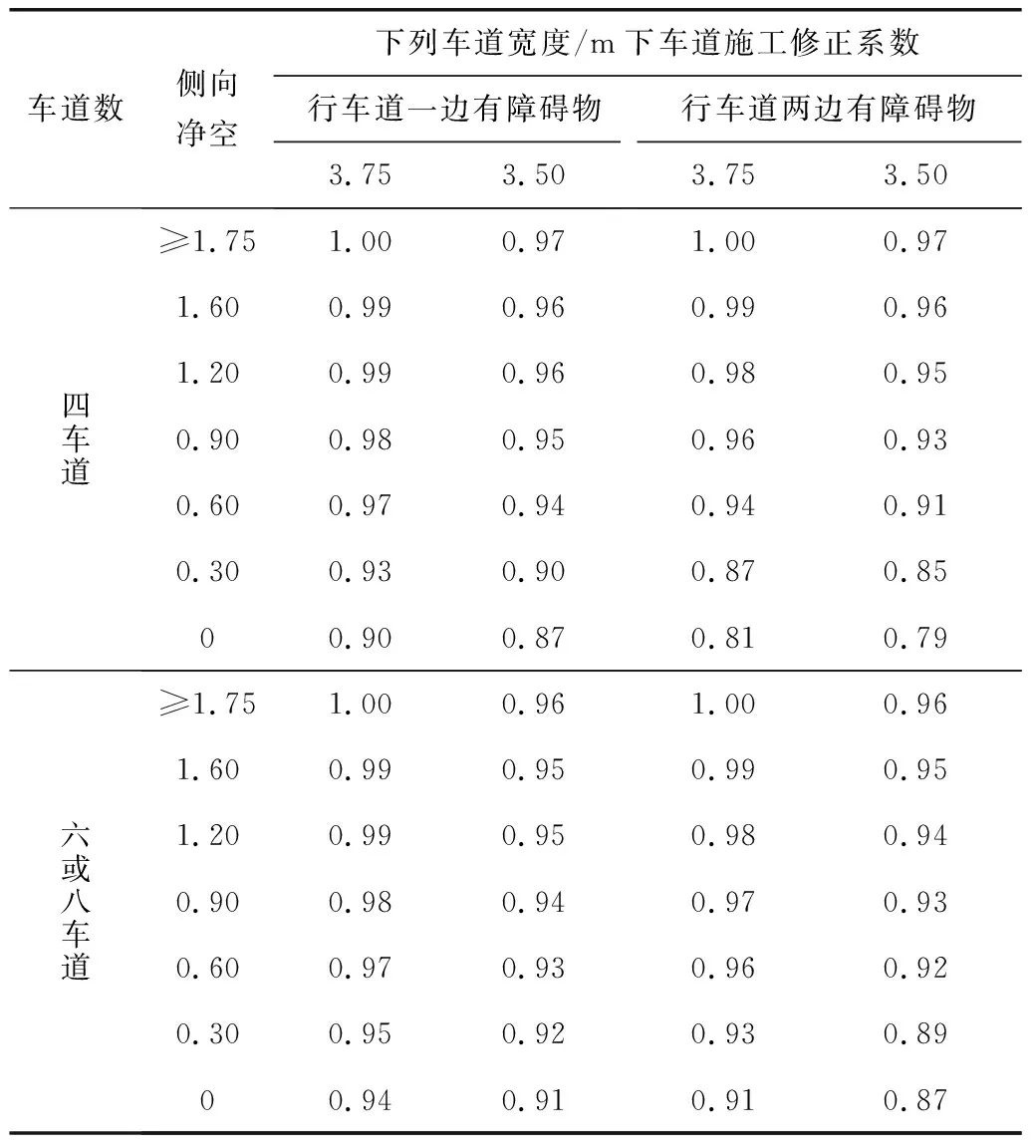
表2 车道施工修正系数Table 2 Lane construction correction coefficients

3)施工区车辆组成修正系数fC。

(3)

式中：pi为车型i占总交通量的百分比；Ei为车型i的车辆折算系数，大中型车Ei=1.5，特大型车为Ei=2.5[11]。

4)路段熟悉度修正系数fp。

路段熟悉度修正系数fp根据驾驶人年龄、驾驶经验是否丰富以及对高速公路行驶路段的熟悉程度而定，一般在0.90～1.00范围内取值[11]。

2 施工环境下高速公路资源调度模型

施工环境下高速公路资源调度模型的核心问题在于如何确定事故点所覆盖的救援范围内各个出救点在经过施工区后能够到达事故现场所需时间及该出救点所能提供的应急物资量[12]。当交通事故发生时，交通指挥调度中心获取事故信息，确定正在进行施工的道路信息，预估事故救援所需的初始救援物资量，且该初始物资量会随着该应急事件持续时间的增长而增加，因此事故点的应急救援物资需求是呈现动态变化的[13]。基于高速公路施工区通行能力C建立以应急救援时间T最短、救援费用Z最低为目标的高速公路施工区应急资源调度优化方案，并使该方案符合出救点的实际情况及各方面的约束条件。

2.1 资源配置模型

由于应急救援物资需求呈现动态变化且施工区较为复杂，为了便于该问题的研究提出如下假设：

1)经过施工区所产生相关的救援费用与该施工区路段通行能力成反比。

2)事故点所需物资数随时间呈线性变化，其增长系数为常数[14]。

在此假设的基础上，研究基于高速公路施工区通行能力的应急资源调度优化模型：

xi≤qi

(4)

(5)

式中：xi为出救点i提供的救援物资量；qi为出救点i储存的全部物资量；Q0为救援所需的初始物资量；a为救援物资量增长系数且该系数为常数；aT-ti和aT为救援物资时间折算系数；T为最短应急救援时间；ti为出救点i抵达事故现场的时刻。

minz1=T

(6)

(7)

(8)

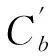
条件(4)表示各应急出救点所能提供的救援物资量应小于等于该点所存储的全部救援物资量；条件(5)表示各应急出救点的救援物资时间折算量的总和应大于该突发事件所需物资时间折算量，以满足救援需求[15]。

施工环境下高速公路资源调度模型可以看作多目标优化问题进行求解。当多个目标(救援时间和救援费用)同时寻求最优时，通常无法满足各个目标均得到最优解，因此利用分层序列法[16]求解上述模型。在应急救援工作中，在无法满足救援时间最短且救援费用最低的情况下，救援时间通常应该是首要的考虑因素。因此在模型求解过程中应首先得到完成应急救援工作时所需最短时间T，然后将该时间作为约束条件，综合考虑施工环境下高速公路的通行能力，得到经过施工区域救援费用最小的应急救援物资调度方案。

定义t时刻事故点物资的需求量Qt及参与救援的物资量St为：

Qt+1=(Qt-St)a

(9)

(10)

式中：Qt为t时刻的剩余物资需求量；St为t时刻参与救援的物资量。

最短应急救援时间根据事故救援点周边各个应急出救点所能够实施救援的时间对各个应急出救点进行时间排序，选取能够实施救援的应急出救点并比较其所能提供的救援物资量是否满足救援点需要，当Qt+1≤0时，救援需求得到满足，此时刻为最短应急救援时间；当Qt+1>0时，表明救援点需要更多的出救点进行救援，不断重复上述过程直到救援需求得到满足[17]。

通过迭代得到最短应急救援时间T，因此将上面得到的模型简化为单目标模型：

(11)

S.t.：

xi≤qi

(12)

ti≤T

(13)

Q0aT≤xiaT-ti

(14)

条件(13)表示出救点i参与救援的时刻应早于完成应急救援工作时所需最短时间T[18]。

2.2 求解应急资源调度模型算法设计

贪婪算法是一种不追求整体最优解，只希望得到当前步骤较为满意解的方法，一般可以快速得到满意的解，因为它省去了为找最优解要穷尽所有可能而必须耗费的大量时间。由于应急资源调度问题逐步进行，判断各步骤是否满足救援需求，因此利用贪婪算法寻求每个步骤的最优解，算法流程如下：

步骤一：获取事故救援信息，令当前时刻为初始时刻，根据现场情况预估救援需求量Q0，将事故点区域附近符合要求的出救点放入集合A1。

步骤二：按照集合A1中出救点抵达事故地的时间顺序逐个进行救援，抵达事故地的时刻为t，记录其提供的救援物资量St。

步骤三：判断并计算当前事故需求物资量与出救点已经供给的救援物资量的差值Δ=Qt-St，若Δ>0，则表明当前这些出救点提供的物资量并不能满足救援，继续在集合A1中寻求其他出救点进行救援。按照式(9)计算当前时刻事故地的救援需求量Qt，进行迭代，转步骤二；若Δ≤0，则表示救援已经完成，满足救援需求，当前时刻为最短救援时间T，转步骤四。

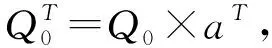
步骤五：将集合A2中所有出救点的能力费用比由大到小进行排序，并按照该顺序选择费用比较高的点进行救援。

3 实例分析

依据山东济青高速段某时间突发事件的历史救援数据对建立的施工环境下高速公路应急资源调度模型进行验证。

济南至青岛高速公路改扩建工程第6标段共计51.175 km(含G20青银高速28.965 km，济广高速公路22.21 km)，如图1。

图1 山东济青高速救援点示意Fig. 1 Rescue points diagram of Ji’nan-Qinghai section of Shandong expressway

假设图1中圆圈位置处发生事故，需要进行应急资源救援，各出救点位置如图1中序号1～6，出救点的基本信息如表3。

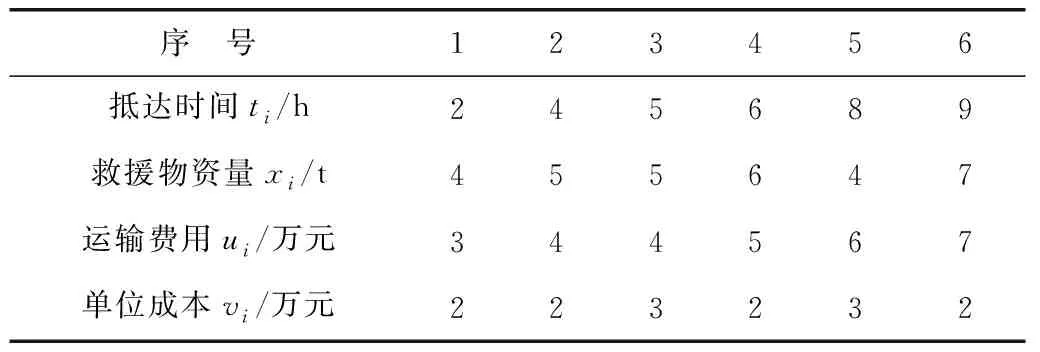
表3 出救点信息Table 3 Information of rescue spots

假设在图1中圆圈处发生事故需要进行救援，初始时刻t=0时预估的物资需求量Q0=20 t，救援物资需求量会随着时间增长呈线性变化，其增长系数a=1.05。根据式(9)、式(10)迭代计算最短应急救援时间，通过步骤三的计算过程可以得到计算结果如表4。

表4 最短应急救援时间的计算Table 4 Calculation of the shortest time of emergency rescue

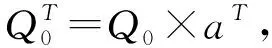
(15)

根据步骤四能力费用比的计算公式逐个计算T=9时刻下所有应急出救点的能力费用比，计算结果如表5。

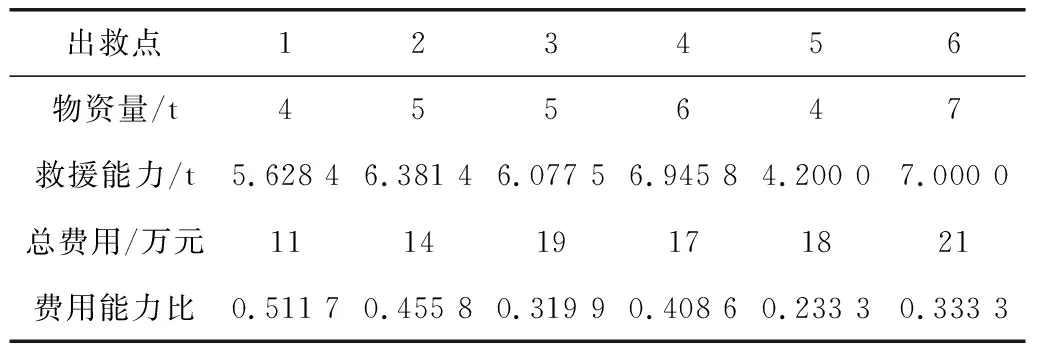
表5 各应急出救点救援能力比较Table 5 Comparison of rescue ability of various emergency rescue points

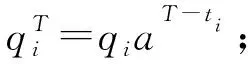
当出救点与救援点之间由于施工造成了路面封闭、车道变窄，导致通行能力的降低，势必会造成该点出救费用的增加以及折算能力费用比的降低。假设出救点1、4与救援点之间进行施工，以山东高速公路改扩建工程为例，对施工路段可能出现的情形进行考虑，分析其道路通行能力。

情形一：设计速度为100 km/h的双车道高速公路，此时道路通行能力Cb=2 100 pcu/h/车道，施工区车辆组成修正系数fC=1，车道数n=2，驾驶人路段熟悉度修正系数fp=0.95。由式(1)可得C=2 100×0.9×1×0.95×2=3 591 pcu/h/单向。

情形二：设计速度为100 km/h的高速公路进行半封闭施工，保留单车道通行，此时道路通行能力Cb=2 100 pcu/h/车道，施工区车辆组成修正系数fc=0.85，车道数n=1，驾驶人路段熟悉度修正系数fp=0.95。由式(1)计算得C=2 100×0.97×0.85×0.95×1=1 645 pcu/h/单向。

将计算得到的施工区实际通行能力代入式(11)重新计算所需费用，并计算得到施工条件下高速公路各应急出救点的费用能力比，如表6。

表6 施工环境下各应急出救点救援能力比较Table 6 Comparison of rescue ability of various emergency rescue points under construction environment

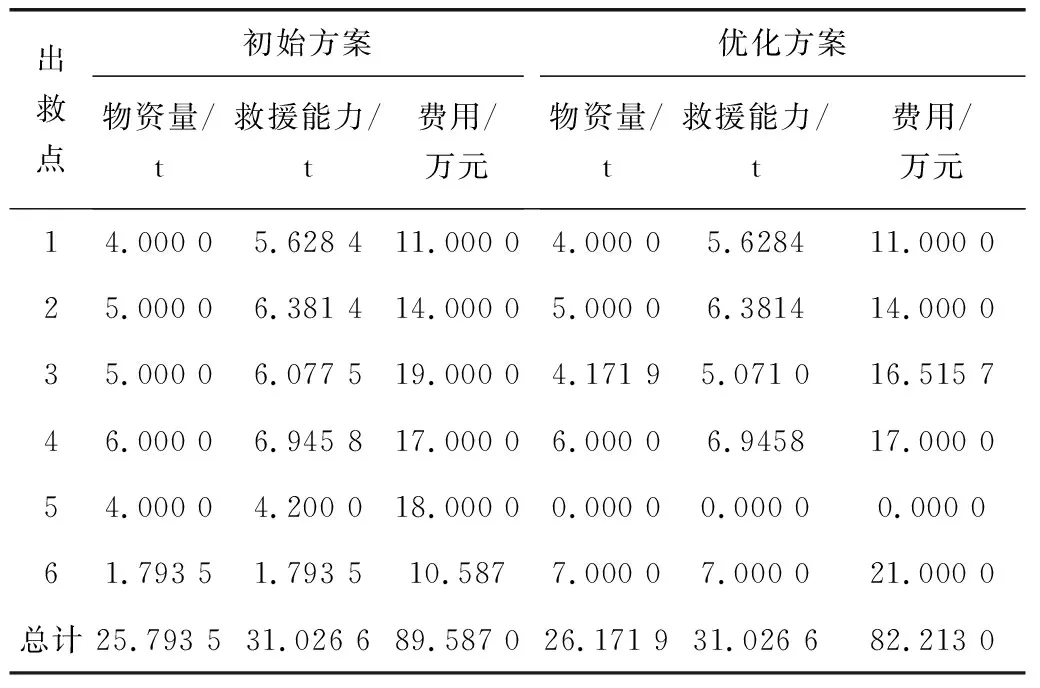
表7 常规环境下方案对比Table 7 Scheme comparison under regular environment

考虑施工条件时,各个出救点费用能力比发生了变化，此时提供的救援物资量和所需费用如表8。

表8 施工环境下方案对比Table 8 Scheme comparison under construction environment

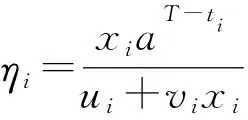
建立的优化方案具体数据对比如表9。

表9 方案对比Table 9 Scheme comparison

经过笔者算法优化后的优化方案所需救援物资量为26.739 3 t，救援费用为101.822 7万元。与初始方案相比，优化后的方案救援物资量增加了0.945 8 t，但是救援费用减少了16.036万元，即物资量虽然增加了3.6%，而救援费用减少了13.6%，救援费用大大降低。

4 结 语

以高速公路施工区通行能力为基础，提出了施工环境下高速公路应急资源调度方法及其相应算法。该算法所需数据获取简单、计算快捷，能够有效地选取合适的救援路线参与救援并降低13.6%救援费用。高速公路施工区是高速公路路段中环境较为复杂、事故率高发的区域，其影响因素较多，目前该算法考虑的因素还不够全面，在之后的研究会进一步加以完善。