基于惩罚-激励变权的TOPSIS法边坡安全评价模型

杨春风， 任雁飞， 王可意

(1. 河北工业大学 土木与交通学院，天津 300401； 2. 河北工程学院 土木工程学院，河北 邯郸 056000)

0 引 言

我国公路建设逐渐由平原区到地形复杂山区建设过渡，公路等级也逐渐变为高等级公路建设，为保证道路施工以及运营阶段的安全，边坡稳定性问题显得尤为重要。

边坡稳定性分析是一个多因素耦合的复杂系统，具有随机性和模糊性，对于边坡稳定的评价国内外已有大量学者进行了研究，如J. BHATTAC HARYA等[1]、洪海春等[2]在考虑影响边坡稳定性主控因素基础上建立基于模糊综合评价的边坡评价模型；杨乐等[3]采用灰色关联度法分析边坡危险性影响因子影响程度；B. K. LOW等[4]提出主成分分析法对土坡评价指标数据排序达到敏感性分析的目的；Y. LEAN等[5]、夏元友等[6]通过边坡状况数据为学习训练样本建立神经网络预测模型达到预测边坡稳定性功能。这些方法各有优势但是存在着模糊评价隶属度方法选择存在争议、灰色关联最优值难以确定、主成分分析指标覆盖性减小、神经网络学习样本不足误差增大的缺点。

此外在评价因素指标权重计算方面，传统的常权综合评价方法会出现某项评价指标状态很差，边坡明显处于不稳定状态，但综合评价结果却显示在安全范围情况，这与实际边坡情况大不相符，导致评价模型无使用价值。TOPSIS法作为多目标决策分析方法，被广泛用于医疗、岩爆、水质、物流等研究领域中，龚剑等[7]在岩爆倾向性预测上应用了TOPSIS法；王小焕等[8]采用TOPSIS模型评价三峡库区水质；潘雨红等[9]将TOPSIS方法用于物流供应商选择中，但在边坡评价方面并没有过多的研究。

因此，笔者在总结前人研究成果的基础上，采用层次变权和TOPSIS法相结合的评价模型，应用于边坡稳定性评价中，以达到对所研究边坡合理、准确的评价。

1 评价模型建立

TOPSIS法是通过对指标数据处理后建立的决策矩阵，列出其中的最优方案和最劣方案，通过计算评价对象与最优方案和最劣方案的加权欧氏距离进行排序，评价对象距离正理想解越近、离负理想解越远时为最优对象。其方法是对结果集进行排序，取其最优解，是对结果的评判方法[10]。

1.1 边坡稳定性评价指标

评价指标的选取尤为重要，既要分析各指标间的相关性程度又要考虑评价指标的覆盖程度，参考相关研究成果以及《高速公路路堑高边坡工程施工安全风险评估指南》中推荐的边坡高度、岩性、坡率、坡体结构、降雨强度、地下水、自然灾害影响等10项边坡稳定性评价指标[11]，并结合工程实际情况进行相关指标的拟定改进，其中定性指标采用百分制的赋值法来定量化处理，具体赋值的标准见表1。

表1 边坡稳定性总体风险评估指标体系Table 1 Overall risk assessment index system for slope stability

1.2 构造决策矩阵

设某一决策问题其决策矩阵为A，决策矩阵中fij(i=1,2,…,n;j=1,2,…,m)代表第i个样本的第j个评价指标,其中n表示组成样本集的样本个数，m表示每个样本评价集中评价指标的个数：

(1)

1.3 归一化决策矩阵

由于选取的评价指标性质各不相同，原始数据指标中同时具有低优指标(数值越小越优)和高优指标(数值越大越优)之分，为使各指标之间具有可比性，对评价指标数据进行归一化及同趋势化处理得到归一矩阵，以下分别是低优指标和高优指标数据处理公式：

(2)

1.4 加权决策阵

各评价指标对应评价对象的影响程度必然是不同的，将各指标的权重与归一化决策矩阵对应指标相乘得到加权归一化后的决策矩阵。其中WT={w1w2…wm}为指标权重：

(3)

1.5 正负理想解与相对贴近度分析

首先确定理想解和负理想解，如果决策矩阵中元素Zij值越大则表示方案越好：

(4)

以欧几里得范数作为距离的测度，则从任意可行解Zi到正理想解Z+和负理想解Z-的距离为式(5)：

(5)

那么某一可行性解对于理想解的相对贴近度定义为

(6)

若Zi为理想解，则相对应的Ci=1；若Zi为负理想解，则相对应的Ci=0。越靠近理想解Ci越接近1，反之，则越接近0，通过对相对贴近度排序求出满意解，以此来实现对样本的评价。

2 权重的确定

对于边坡稳定性评价最重要的是指标的权重选取，普通的权重确定方法大多是以常权重为基础，但不同地域不同边坡势必指标权重有所不同，即便是同一个边坡，当某个因素劣化程度很高时，不做相应的权重调整也会导致最终的评价结果失真，真实性和准确性都无法保证，变权法可以根据指标取值对指标进行相应的激励或惩罚，从而更加准确的评价出边坡稳定性的真实状态。

2.1 层次分析法

采用专家学者来当决策者，其长期的工程经验增加了判断矩阵的合理性。决策者通过在其对应目标意义下的多个因素进行评价，通过因素之间两两比较构造判断矩阵，在此选用9标度评价表，笔者在此不做赘述，具体原理及步骤可参考文献[12]。

2.2 惩罚-激励型变权函数

变权原理的思想是根据指标因素取值变化，使其权重随之发生变化，当评价指标的测量值较差时，会增加这项指标的权重，既对危险指标进行惩罚，当评价指标的测度值较好时，会在一定程度上减小这项指标的权重，既对良好指标进行奖励，同时通过引入均衡函数来调节某项指标权重，改变对整体评价的影响，由变权原理，笔者采用局部惩罚-激励型变权函数：

(7)

(8)

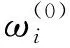
由惩罚-激励型变权函数确定的指标权重应用于TOPSIS法分析模型中，整体评价流程如图1。

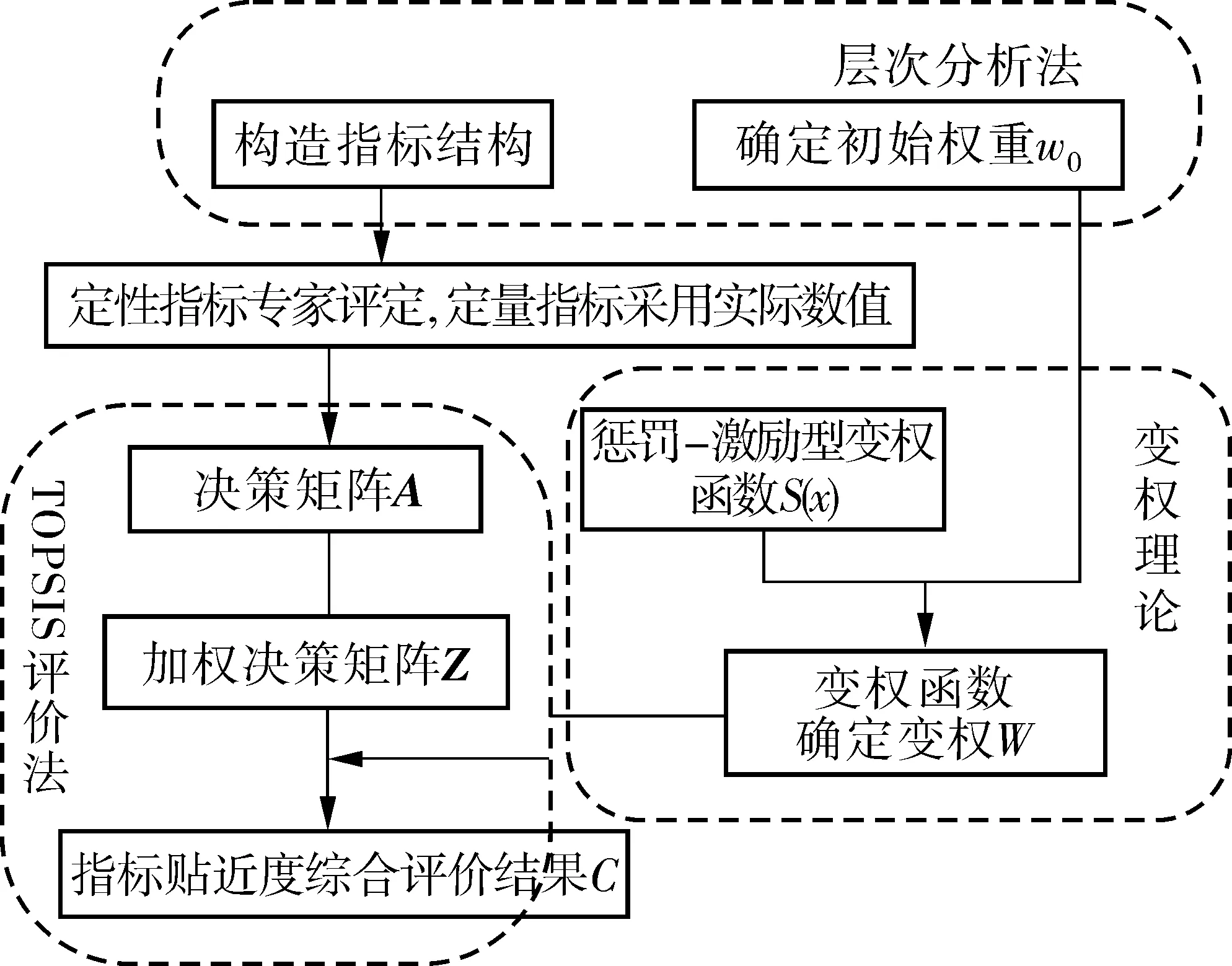
图1 惩罚变权TOPSIS法评价流程Fig. 1 Evaluation process of penalty variable weight TOPSIS method

3 工程实例分析

以建设中的京(北京)—新(新疆)高速张家口段公路边坡为例，作为河北省高速公路网规划中“横1”并行线的重要组成部分，张家口段高速路地属山岭重丘地形地貌，有大量高边坡深路堑，并且80%的路段为轻微湿陷性黄土，其工程边坡的稳定性问题十分突出。在此选择S1：K23+500～K23+780，S2：K40+980～K41+150,两标段的典型边坡进行评价。

3.1 边坡概况

根据现场实际工程勘察，此两段边坡的工程地质条件如下：

S1：K23+500～K23+780段边坡高度为46 m，坡长为127 m，直行坡，坡段有少量低矮灌木，坡脚大量碎石堆积，岩石风化作用强烈，片理发育，路段多为湿陷性黄土，部分区域为泥岩，结构面及其组合面的倾向与边坡倾向之间的夹角约为45°，地下水位于边坡上部30 m处，年均降雨量约为500 mm ,边坡采用注浆和部分锚固的加固措施。

S2：K40+980～K41+150段边坡高为38 m，坡长为254 m，有少量低矮灌木，石风化作用强烈，地层岩性、自然灾害、降雨量与边坡S1大致相同，结构面及其组合面的倾向与边坡倾向之间的夹角约为40°，水位位于边坡上部27 m，边坡采用注浆工程加固措施，各评价指标的实测数据如表2。

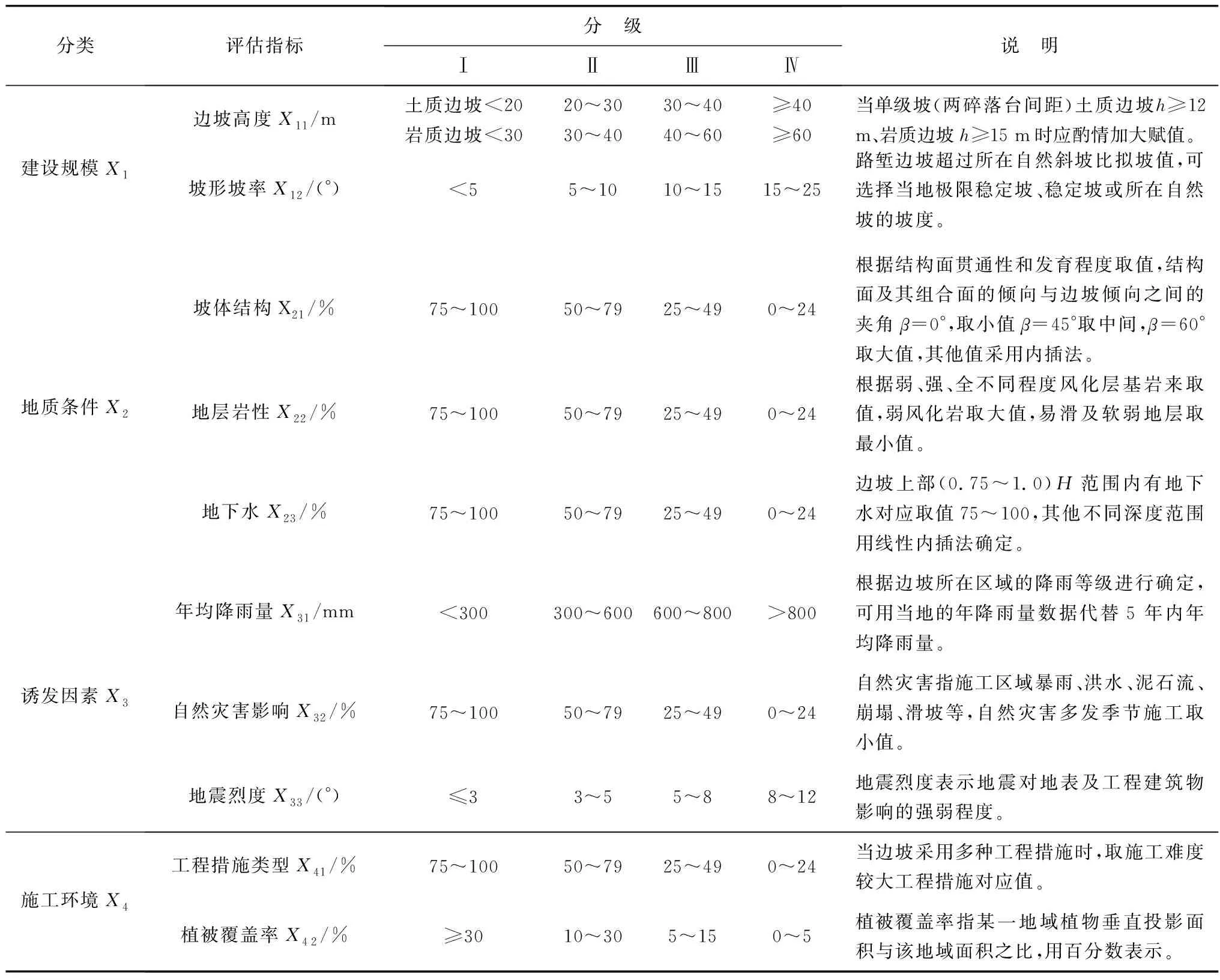
表2 边坡评价指标实际值Table 2 Actual value of slope evaluation index

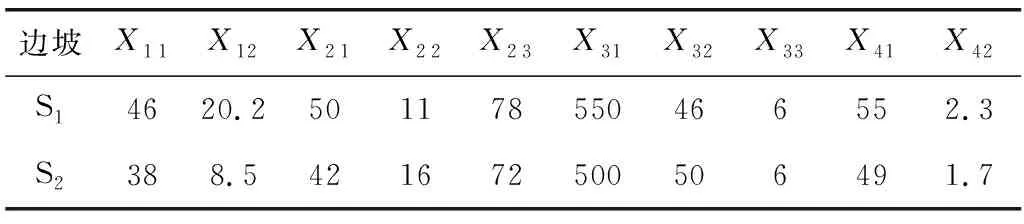
边坡X11X12X21X22X23X31X32X33X41X42S14620.2501178550466552.3S2388.5421672500506491.7

3.2 权重计算

根据层次分析法计算初始权重，建立如图2的二级评价指标体系，确定指标权重值，并对所有底层指标权重进行总排序，根据构造的判断矩阵求得最大特征值为4.07,C.R=0.026<0.1，满足一致性检验要求，计算得到二级权重矩阵为

W=[0.201,0.268,0.388,0.143]

根据二级权重值计算得10个底层指标权重总排序矩阵为

θ=(θ1,θ2,…,θ10)=(0.105,0.105,0.052,0.116, 0.107,0.248,0.115,0.033,0.075 ,0.044)

图2 评价指标层次结构Fig. 2 Evaluation index hierarchy chart

θ即为各指标的初始权重值w0，通过三维空间图构建各参数取值变化对函数S(x)结果的变化规律以此确定参数的取值，为建立合理的变权向量函数S(x)。本文参数取值分别为μ=0.4，λ=0.5，α=0.8，β=0.9，K=0.15，C=0.2，c1=0.5，c2=0.7[14]，由此得到变权向量函数表达式如下：

由此可以看出变权函数的特强惩、强惩和初惩区间分别在(0,0.4)、(0.4,0.5)和(0.5,0.8)上，受激励区间为(0.9,1)，通过变权函数根据边坡评价指标实测值、初始权重值计算得到变权权重值w(表3)。

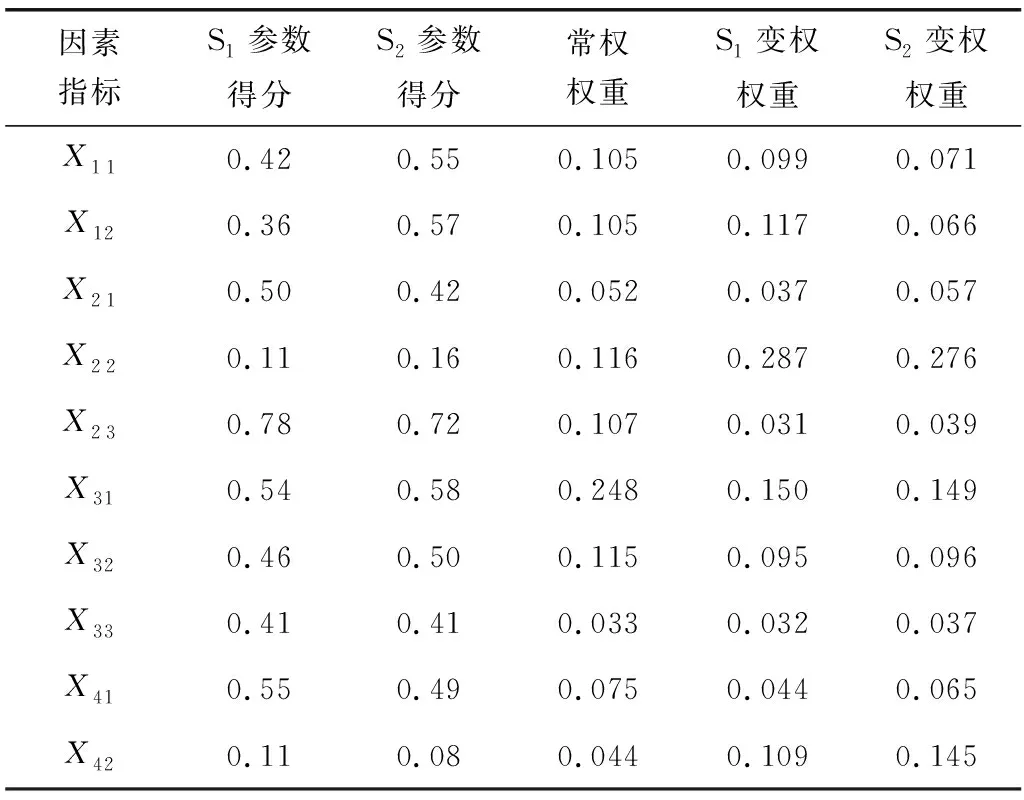
表3 高速公路边坡指标参数得分及权重Table 3 Score and weight of highway slope indicator parameters

由表3可见，变权之后的权重较初始权重均发生了变化，这是因为参数得分低的指标落在惩罚区间，通过惩罚函数增大了权重，参数得分较高的指标调整之后适当减小了权重。

3.3 TOPSIS模型综合评判

根据边坡稳定性分析的单指标分类区间将稳定性评语划分为4个等级，稳定Ⅰ，较稳定Ⅱ，较不稳定Ⅲ，不稳定Ⅳ，根据实测数据以及指标权重构造加权决策阵，由评价公式式(2)～式(6)得到评价指标对应正负理想解的欧式距离及贴近度矩阵，分别使用常权权重和变权权重进行综合评判，结果如表4。

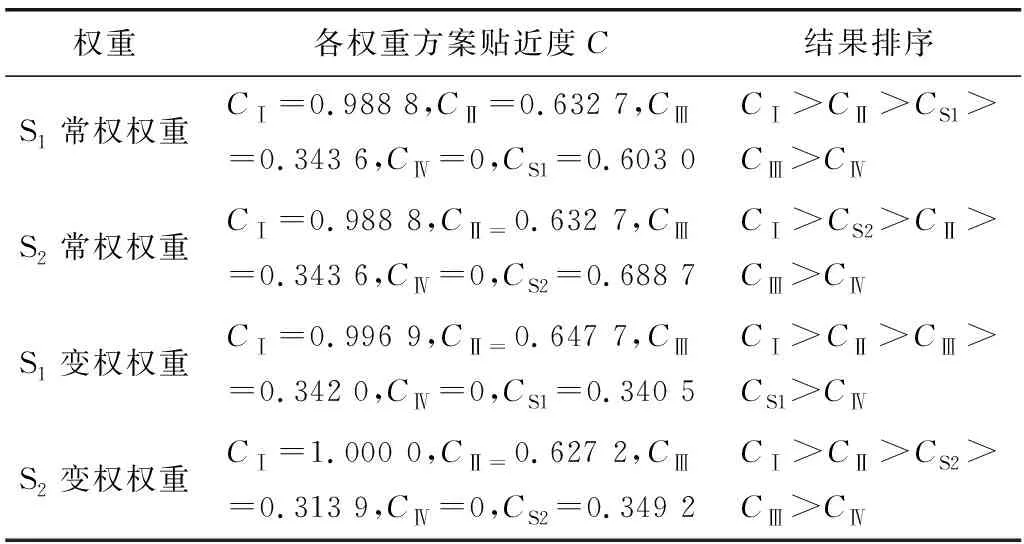
表4 边坡稳定性TOPSIS评价结果Table 4 TOPSIS evaluation results of slope stability

根据贴近度的大小比较可以看出，采用变权权重评价结果显示，边坡S1处于稳定性等级Ⅳ不稳定状态，边坡S2处于稳定性等级Ⅲ较不稳定状态，而常权重的评价结果显示，边坡S1处于稳定性等级Ⅲ较不稳定的情况,边坡S2处于稳定性等级Ⅱ较稳定的情况，现场实际情况中，边坡S1发生了边坡滑坡现象，因此采用变权评价更符合现场实际情况，得到的评价结果更为可靠。

同时选择底层岩性这项评价指标进行分析，图3为底层岩性指标值变化时边坡的两种综合评价结果以及变权权重变化情况。由图3可以看出常权情况下底层岩性改变对稳定性评价结果影响较小，不能很好反映出这项指标变化对综合评价的影响，而当底层岩性变差时，即指标值变小时通过变权函数作用其权重上升，增加了这项指标的重要程度，在此作用下综合评价得分降低，当底层岩性指标值低于45时，变权评价结果与常权评价结果差异较大，指标值超过75时，常权评价结果和变权评价结果趋于一致，因此，变权可以更好的反映指标状态变化对边坡稳定性结果的影响。

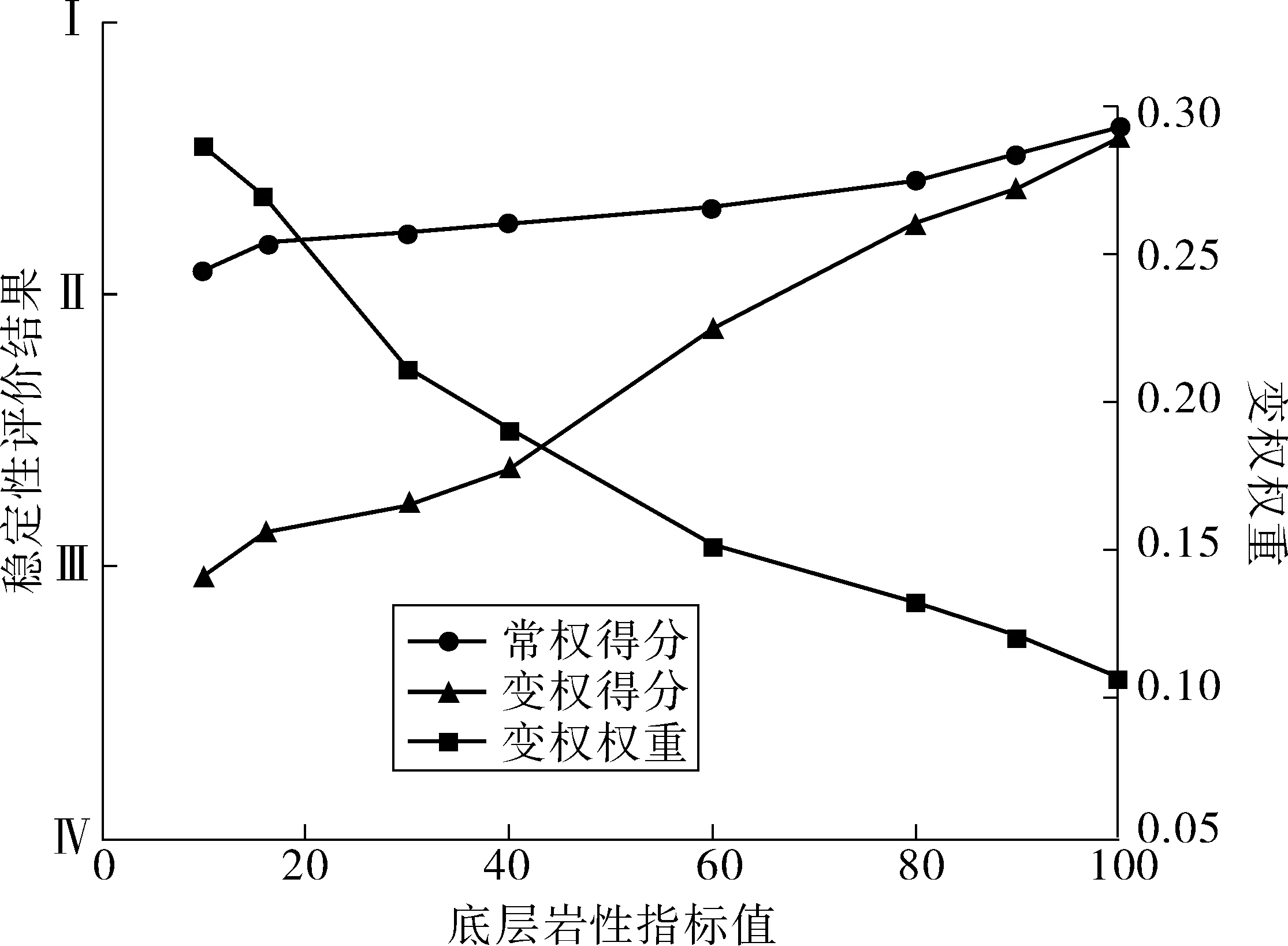
图3 底层岩性指标值变化评价结果Fig. 3 Evaluation results of changes of bottom lithology indicator value

4 结 论

1)笔者将层次变权法用于TOPSIS评价模型中，通过惩罚-激励变权函数对评价指标进行变权，通过提高劣化指标的敏感程度体现出对最终评价的影响，克服传统评价方法因素多、权重难以分配以及常权赋权法造成的偶然性和局限性，使评价指标赋权结果更符合实际情况。

2)TOPSIS评价方法过程严谨、计算方便，不仅可以评判出边坡所处稳定性等级，还可以直观观测边坡所处稳定性程度，是传统评价方法所没有的，有较高的实用价值。

3)结合京新高速K23+500～K23+780、K40+980～K41+150两段边坡的评价，并与常权结果进行比较，验证了变权TOPSIS评价模型应用于边坡稳定性评价的准确性及实用性，为今后公路边坡稳定性评价分析提供了一种新思路。