基于两次聚类的PWARX驾驶行为辨识模型

应海宁， 唐振民， 韩 旭

(1. 南京交通职业技术学院 电子信息工程学院，江苏 南京 211188；2. 南京理工大学 计算机科学与工程学院，江苏 南京 210094)

0 引 言

近年来，随着机动车保有量急剧上升，机动车驾驶员的驾驶行为对交通安全和自然环境影响越发明显[1]。驾驶行为建模是对驾驶状态进行辨识、理解和预测的有力手段，已有很多学者对其展开了研究[2-4]。但驾驶行为会受驾驶员的驾驶习惯、驾驶状态及交通状况等多种因素的影响，因而目前为其建立高精度辨识模型还存在很多困难[5-6]。S.D.KEEN等[7]和P.ANGKITITRAKUL等[8]分别采用结构简单、运算方便的线性控制器建立了驾驶行为模型；但该类方法在建模精度方面不够理想。神经网络、隐马尔科夫等非线性模型以其良好非线性模型逼近能力在驾驶行为建模领域得到了广泛应用[9-10]。学者们发现驾驶行为在逻辑上可抽象为由驾驶决策过程和驾驶控制过程两部分组成；前者可用各个由离散事件驱动的分段模式来描述；后者则可由各个分段子模式中的连续时变系统来表征[11-13]。也就是说，驾驶行为模型实际上可看为是一个由离散子系统和时变连续性子系统组成的混杂系统(hybrid system,HS)。

迄今，学者们提出了很多针对HS驾驶行为的建模算法。J.H.KIM等[14]提出了分段线性和混合整数建模的MILP(mixed integer linear programming)算法；但该算法只讨论了避免碰撞驾驶行为的建模问题。S.SEKIZAWA等[15]将隐马尔可夫模型(hidden markovmodel, HMM)嵌入到自回归各态历经模型(auto regressive exogenous,ARX)中的各个离散状态模型中；该算法依据模型转移概率实现了各固定子状态模型间的切换，但没有考虑整个系统的拟合精度。T.AKITA等[16]提出了一种分段仿射自回归各态历经算法(piecewise auto regressive exogenous, PWARX)，用于对跟车行驶状态进行建模。R.TERADA等[17]提出使用分层策略对驾驶行为HS模型中潜在层次结构进行分析，在各分层空间上再进行分段ARX建模；但该算法对驾驶行为层次分割较为主观，难以保证其具有较好的泛化能力；此外，当子模型之间存在重叠时，PWARX模型辨识精度会受到较大干扰。

基于聚类算法的PWARX模型在HS建模领域得到了广泛应用。该类算法基本思路是通过聚类算法对子模型区域进行无监督划分，然后在各个子空间上再进行PWA建模。于玲[18]提出了一种基于聚类技术，并融合搜索、模式分类和线性系统辨识的PWARX算法(C-PWARX)；该算法不需要预先知道子模型数量，但其搜索子模型区域边界过程的计算复杂度较高。潘天红等[19]利用改进的模糊聚类算法(GK-PWARX)，克服聚类迭代过程出现的非数值解问题，先以综合性能指标最优确定最佳的子模型个数，再利用支持向量机构造出一个标准的二次规划问题，得到凸多面体的方程系数；该方法的建模精度依赖于模糊隶属度合理性。Z.LASSOUED等[20]提出了一种能同时对子模型空间分界面参数和自身参数进行估计的PWARX建模算法(T-PWARX)，该算法结合了聚类、线性模型辨识和模式识别技术，降低了异常点对建模过程的干扰；但在缺少先验知识场合的应用效果还不够理想；为克服对先验知识的依赖，以及非线性准则对目标函数无法确保始终收敛于极小值。Z.LASSOUED等[21]又接着提出了一种基于聚类的PWARX建模算法(DBS-PWARX)，但该算法难以高效处理凸多面体区域的划分问题。受制于聚类算法本身局限性，上述方法普遍存在对子模型区域划分需要依赖一定的先验知识，且需要经过多次迭代搜索和调整才能获得较为准确的凸多面体方程。

针对上述存在的不足，笔者提出了一种融合近邻传播聚类(affinity propagation, AP)和K-means聚类的PWARX模型辨识算法(AK-PWARX)，用于对驾驶行为进行建模。该模型综合两种聚类算法的特点，可在没有先验知识的情况下对PWA子模型区域进行合理划分，以准确获取各个驾驶行为子模型对应的状态样本子空间，有利于提高整个驾驶行为模型的辨识精度。模型时间复杂度只与样本点数量和维度相关，在低维度空间上具有较好地驾驶行为在线辨识实时性能。

1 基础理论

1.1 PWARX辨识算法

PWARX是一种由有限个仿射子模型集成的特殊非线性模型，根据给出的切换律能以任意精度逼近各种连续、光滑、非连续、非光滑的混杂系统。PWA系统模型如式(1)、(2)：

y(k)=fpwarx(rk)+ek

(1)

(2)

在模型结构已经明确的条件下，PWARX模型辨识的基本任务是对参数θi、hij和Ss进行求解。这3种参数之间存在高度耦合，目前尚无明确解法，一般采用搜索迭代等方法来估计。

1.2 AP聚类

AP是一种通过近邻样本之间的信息迭代传播来实现聚类的方法。其特点是不需要事先指定聚类数量，因而具有很好的自适应性。AP算法以样本的相似度矩阵S=[sij]为输入，s(i,j)=-║xi-xj║，i≠j，║·║为欧式距离。样本间传播的消息分为吸引度r(i,k)和归属度a(i,k)两种。其中：r(i,k)用于度量样本k能够吸引样本i为其聚类成员的程度；a(i,k)用于度量样本i将样本k作为其所属聚类中心的适合程度。在迭代过程中，r(i,k)和a(i,k)按式(3)、(4)不断更新。

r(i,k)=s(i,j)-maxk≠k′[a(i,k′)+s(i,k′)]

(3)

(4)

通过阻尼系数λ可调整r(i,k)和a(i,k)的更新幅度，方法如式(5)：

Mt+1=(1-λ)Mt+λMt-1

(5)

式中：M为以r(i,k)和a(i,k)为元素的矩阵。

当吸引度和归属度不再变化时，由式(6)可得聚类结果。

arg max[r(i,k)+a(i,k)]

(6)

1.3 K-means聚类

K-means算法认为同一个簇内的样本之间具有较近距离，其算法过程如下：

1)选取若干个初始聚类中心；

2)根据剩余样本到质心的距离将其归到与质心最近的类中；

3)重新计算已知各个聚类的质心；

4)迭代2)～3)步直至满足停止条件。

初始类聚类中心点(质心)对K-means算法最终的聚类结果有重要影响。

2 AK-PWARX建模算法

表征驾驶行为特征的参数主要包括车辆本身的行驶状态数据和车辆行驶环境的状态数据两类。前者一般通过自诊断系统(on-board diagnostic,OBD)接口即可直接获取，在应用上具有方便、代价低等优点；后者则需要借助各类雷达、摄像头等装置才能获得，其虽能明显提高对行驶环境的解释力，但应用成本和经济成本较高。因此目前已经市场化的驾驶行为辨识系统(如美国Progressive公司的Snapshot等)主要基于前者进行分析。鉴于此，笔者选择基于车辆自身行驶参数对驾驶行为进行建模。

2.1 输入输出参数

驾驶行为安全性评价指标有多种，笔者只考虑高速转弯和急加减速这两种驾驶行为对车辆行驶安全性的影响。由于驾驶行为状态在时域上是一种有序列，对其状态特征参数的在线提取一般是在滑动窗内进行的。笔者在长度为LW个样本点的时间窗内对转向特征值和加减速特征值参数进行提取，如式(7)：

(7)

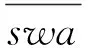
算法的输出参数为驾驶行为危险系数为coe，coe∈[0, 1]；coe值越大表示危险程度越高；coe<0.5表示驾驶行为正常，coe>0.5表示驾驶行为危险。

2.2 建模原理

由于车辆实际驾驶行为会受到多种因素的影响，即使同一个驾驶员在相同交通环境下也会具有不同的驾驶行为。因此要获得明确的子状态数量及其清晰的区域分割较为困难。而PWARX模型参数求解问题最主要的难点就是关于参数S的确定，这就会导致难以获得合理的Ri分布和hij。

笔者提出基于两次聚类的PWARX模型辨识算法(AK-PWARX)，利用AP算法能够自适应挖掘样本空间结构优点，并结合K-means聚类来获得更为合理的驾驶行为状态多面体样本空间划分。

(8)

式中：φi=[ri(1),…,ri(Ni)]T为第i个聚类中Ni个回归系数。

第4步：求解LDi上的多面体划分Ri。设多面体划分的超平面方程如式(9)：

hi={airk+bi=0}

(9)

构造其代价函数如式(10)：

(10)

式中：Pi为回归向量rk属于Ri空间的正确概率；ρ为惩罚因子；μi为概率因子。

式(10)则变为二次优化问题，采用积极集二次规划算法对(ai,bi)进行求解。

(11)

2.3 算法有效性分析

为评估AK-PWARX模型对驾驶行为在线鉴别的实际意义，需要从理论有效性和时间复杂度两个方面去分析其有效性。

2.3.1 理论有效性

鉴于AP和K-means聚类算法的理论有效性已经得到证明，因此AK-PWARX算法的理论有效性主要取决于多面体区域划分Ri的有效性。

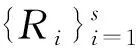
则有式(12)：

(12)

由此可得，笔者所提的PWARX模型的多面体区域分割算法是正确的，这从理论上保证了该算法对任意复杂驾驶行为模型都可获得有效的子模型状态空间，以提高驾驶行为模型的辨识精度。

2.3.2 时间复杂度

设AK-PWARX模型一次需处理的k维样本点数量为N。由于AP算法和K-means算法的时间复杂度为O(kN2)。积极集算法的时间复杂度为O(k2N2)，梯度下降法时间复杂度为O(Nk)。因此，AK-PWARX算法的时间复杂度为O(k2N2)。

3 实 验

3.1 仿真实验

由式(13)定义一个包含3个子模型的PWARX驾驶行为仿真模型，其每个子模型分别对应匀速行驶、急加速和急转向3种正常驾驶行为。

(13)

式中：rk=Uk-1。

该模型共生成了150个驾驶行为的特征样本，每个样本点是一个由u1和u2组成的二维特征向量。整个样本集在归一化后的空间分布如图1。

图1 人工样本分布Fig. 1 The distribution of artificial samples

AK-PWARX算法在图1中样本集上的运行过程如下：

1)通过AP算法在样本集上进行聚类，其结果如图2；

2)在各个类簇上进行PWA线性建模，其拟合结果如图3；

3)使用K-means算法在各类簇模型的参数空间上进行聚类，获得各个子数据集的LDi(图4)，可见K-means算法得到了3个类簇(每个椭圆表示一类)，意味着存在3个不同的PWA子模型；

4)在各个数据集LDi上求解相应的PWA子模型，结果如图5。

由此可看出，整个样本集被准确分成了3个区域，通过在每个区域上对PWA子模型进行求解，得到了最终的PWARX模型。

图2 AP聚类结果Fig. 2 AP clustering results

图3 各类簇上的PWA子模型Fig. 3 PWA sub-models for clusters

图4 数据集LDi的结构分布Fig. 4 The structure distribution of data sets LDi

图5 PWARX模型求解结果Fig. 5 Solution results of PWARX model

3.2 真实实验

3.2.1 实验环境设置

实验车辆采用长安福特2014款翼虎车辆，所需采集参数细节如表1。

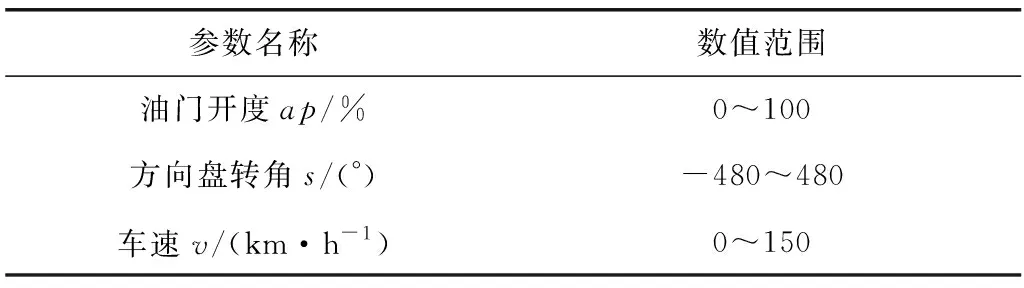
表1 驾驶行为原始数据类型Table 1 Original data type of driving behavior

数据采集设备为飞思卡尔i.MX6Q单片机，该处理器集成了Flexcan模块接口，通过直接访问OBD接口中的CAN总线(数据采样频率为5 Hz)，可实时解析表1中的车辆行驶原始数据；通过3G通信模块可将数据远程传输给服务器；在服务器端通过后台数据处理实现驾驶行为模式辨识。为便于对建模算法的性能进行验证，笔者将所采集的驾驶行为数据在MATLAB2010平台中进行分析处理。车辆数据采集环境如图6。

图6 数据采集环境Fig. 6 The environment of data sampling

由于各类突发交通行为(如拥堵、车辆不按交通信号行驶等)对个体的驾驶行为影响较大，所以笔者只关注在正常交通通畅且没有其余车辆干扰状态下的驾驶行为辨识问题。考虑到实际驾驶行为的危险程度在定义上具有一定模糊性，根据福特翼虎车辆物理特性和相关技术[22-23]，笔者将车辆急减速大于1.5 g，侧加速度大于0.5 g时的驾驶行为定性为危险驾驶(coe>0.5)。

笔者对10位驾驶员在南京交通职业技术学院驾训场地内某相同路段(包含220 m直道、2个直角弯道和30 m的“8”字形弯道)上的驾驶行为进行建模和辨识。车辆行驶状态数据分别在正常驾驶行为和危险驾驶行为状态下进行采集。根据驾驶员驾驶行为差异和数据采样设备的采样率等因素，根据驾驶行为样本的采集方法[24]，本实验共采集了450组驾驶行为参数样本，每组样本包含1 000个样本点，具体如表2。

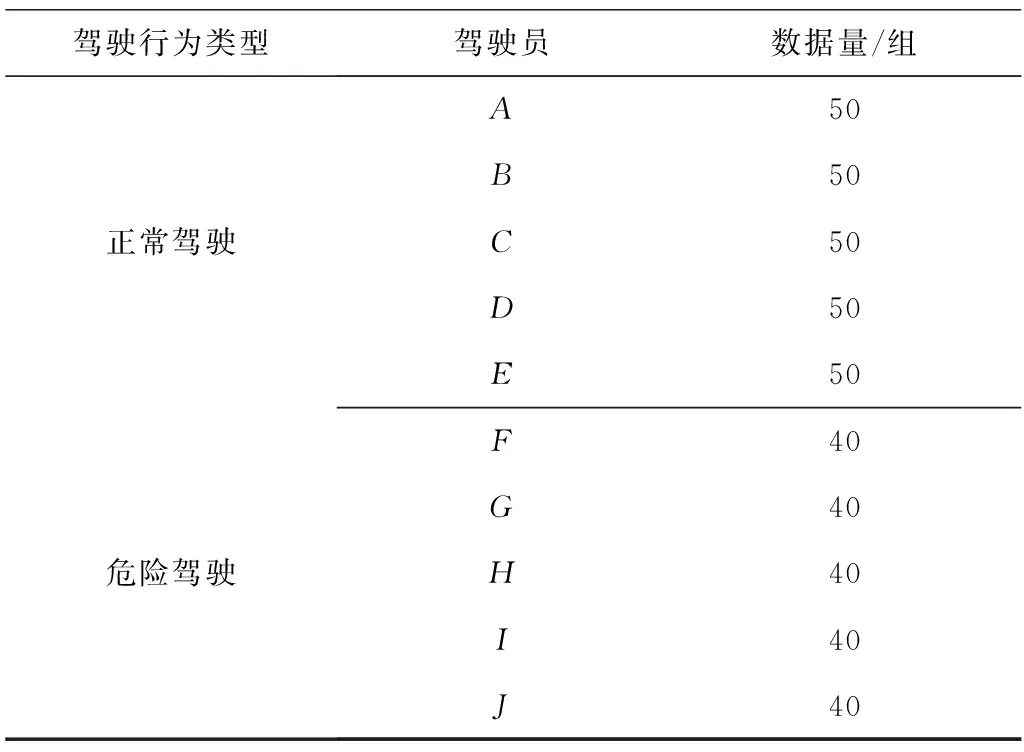
表2 驾驶行为原始数据Table 2 Original data of driving behavior

图7为某组危险驾驶状态下的车辆行驶原始数据样本。图8为3种原始参数计算所得的u1和u2值(LW=10)。

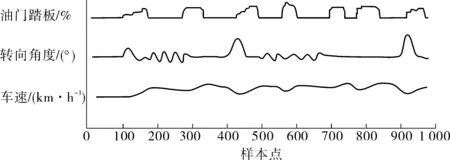
图7 危险驾驶行为原始数据样本Fig. 7 Original data samples of dangerous driving behavior

图8 某组驾驶数据样本的特征参数Fig. 8 Characteristic parameters of a group of driving data samples

3.2.2 实验结果

驾驶行为模型可被看成是由随机事件驱动。根据均值理论，将训练所得的PWARX模型参数均值直接作为测试用PWARX模型参数是合理。笔者在450组驾驶行为参数样本上，采用5折交叉验证法对AK-PWARX平均建模精度进行统计。图9为任意选取的10组由PWARX模型参数u1、u2和coe构成的向量在三维空间上分布。

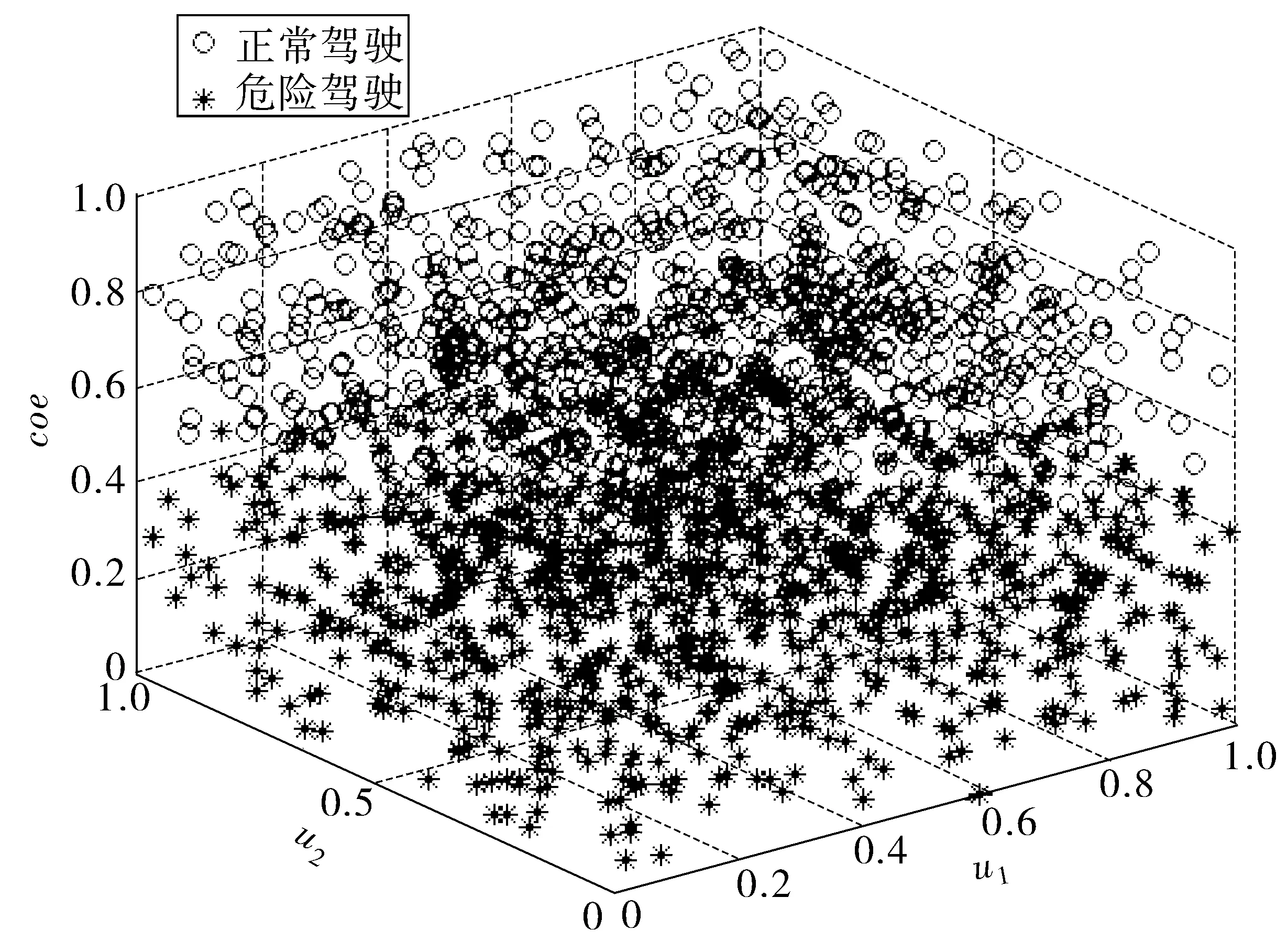
图9 某组样本的PWARX模型参数分布Fig. 9 Parameter distribution of PWARX model for a set of samples

为了验证AK-PWARX算法性能，笔者在相同实验环境下与C-PWARX、GK-PWARX、T-PWARX和DBS-PWARX算法建模精度进行比较，具体结果如表3。

表3 各算法的驾驶行为建模精度Table 3 Accuracy of driving behavior modeling based on various algorithms

由表3可看到，AK-PWA算法对驾驶行为的建模平均准确率要高于其他模型，取得了较好效果。

4 结 语

笔者提出了一种基于AP聚类和K-means聚类的PWARX模型(AK-PWARX)，用于对驾驶行为进行辨识。该模型先后在样本和参数空间上两次调用聚类算法，利用两种聚类算法各自技术特点，在没有先验知识情况下对PWA子模型区间进行高质量划分；并在其基础上通过梯度下降法对PWA模型参数进行求解。使用OBD接口数据采集设备对由10个驾驶员产生车辆驾驶数据进行采集，在该数据集上用AK-PWARX算法进行建模，取得了91.5%的精度。

但是笔者采用数据集只涉及到了车辆本身行驶状态，而没有考虑车辆环境行驶状态。因此，随着车辆行驶环境感知设备成本的下降，有必要研究如何融合车辆行驶环境数据来进一步提高驾驶行为的建模精度。