一种基于KPCA和Brovey变换的遥感影像融合方法

柯宏霞， 高建平

(重庆交通大学 土木工程学院，重庆 400074)

随着多平台、多时相、多光谱及多分辨率遥感卫星系统的大量涌现，可见近红外、短波红外、热红外、微波等多源遥感数据资源日益丰富[1]。而遥感影像融合技术能够充分、有效地提取多源遥感数据的优势信息，提高遥感影像的光谱分辨率和空间分辨率，从而克服遥感影像自动介意中单一信息源不足的问题[2]。其中，多光谱数据和高分辨率全色数据的融合是遥感影像融合研究的重要方向之一。

迄今为止，已经发展多种遥感影像融合方法，总体上分为分量替换法和多尺度分析法两大类。分量替换法基本思想是将全色影像的空间信息融进多光谱影像，经典的算法包括Brovey变换[3]、亮度-色度-饱和度变换(HSV)[4]、主成分分析(PCA)[5]和GS变换[6]等，得到了较好的融合效果，但都存在光谱畸变的问题。多尺度分析融合算法如小波变换法[7]、NSCT[8]、CBD[9]、基于亮度平滑滤波调节法[10]和MTF-GLP[11]方法，此类方法将全色波段的细节信息注入到多光谱影像，得到的融合影像光谱连续性好，但是计算复杂[12]，会损失一些高频信息[13]。

研究表明：Brovey变换比传统的HSV、PCA更适合多光谱与全色波段数据之间的融合，其算法简单、快速，高频信息融入度更高[14]，但该算法仅利用3个多谱波段与全色波段进行融合，光谱失真严重。近年来涌现出一些改进的Brovey算法如可调性HIS-Brovey[15]、PCA-Brovey[16]、Brovey-Wavelets[17]，这些研究都取得了较好的融合效果， 但是这些算法不仅数据利用率低，而且仅考虑原始影像中的线性光谱数据，导致融合结果中缺乏非线性光谱信息，降低了光谱信息的保有性。KPCA能在PCA的基础上，通过引入核函数把数据非线性映射到一个高维空间，重组光谱数据的内部结构，最后进行PCA特征提取，从而提升了算法降维和遥感影像非线性数据挖掘的能力。因此，笔者提出一种基于KPCA和Brovey的遥感影像融合方法，对武汉市和佛山市的两组数据进行融合，同时，利用经典的PCA-Brovey算法对同组数据进行实验，并通过定性和定量融合评价指标进行对比分析。

1 KPCA-Brovey融合基本原理

1.1 Brovey基本原理

Brovey变换融合又称比值变换融合，原理简单，容易实现。该方法是通过归一化后的多光谱波段与高分辨率影像乘积来增强影像信息[18]。由于方法仅能对3个波段进行融合，光谱信息利用率低，造成融合影像光谱扭曲。经过Brovey融合后的新波段结果图像灰度如下：

(1)

其中B1_new、B2_new和B3_new表示融合后的影像数据，B1_original、B2_original和B3_original表示原始MS中的3个波段，BPAN_original表示原始的PAN影像[2]。通过简单地波段混合运算，将高分辨率和多光谱优势融合在一起。利用KPCA提取的3个核主成分KPC1 、KPC2和KPC3作为Brovey算法的原始输入影像。

1.2 KPCA基本原理

PCA在数据压缩领域有着广泛的应用，尤其针对线性数据集；但对于非线性数据，PCA则表现出不稳定性。为解决这一问题，学者们提出KPCA算法。它先利用核函数把数据非线性映射到一个高维核空间，然后在该空间中进行PCA线性变换。研究表明，KPCA在数据压缩能力和挖掘非线性特性能力上明显优于PCA算法。其基本原理[19]如下：

设：xi∈RP(i=1,2,…,n)为输入样本点，把输入空间RP通过非线性变换Φ(x)映射到特征空间F,即

Φ(x)：RP→F

(2)

定义核函数K表示为

K=Φ(x)TΦ(x)=[k(xi,xj)]n×n

(3)

其中，

k(xi,xj)={Φ(xi),Φ(xj)}=Φ(xi)TΦ(xj)

(4)

此时，在F空间中，协方差矩阵为

(5)

协方差矩阵C的特征值为λ，特征向量为V,则

λV=CV

(6)

特征向量V是由{Φ(x1),Φ(x2),…,Φ(xn)}张成的子空间。

则必然存在α={α1,α2,…,αn}满足：

(7)

将式(4)，式(5)，式(6)和式(7)联合整理后可得

(8)

经过化简可得：

nλα=Kα

(9)

其中K矩阵经过数据中心化后为

(10)

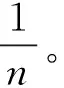
核函数K需要满足Mercer条件。常见的核函数有：

④向8只烧杯中依次加入等量适量清水、2×10-11、2×10-10、2×10-9、2×10-8、2×10-7、2×10-6g·L-1的2，4-D溶液。

1)线性核函数K(xi,xj)=xj+1

4)Sigmoid核函数

K(xi,xj)=tanh(axixj+c)，其中a为Sigmoid核函数的宽度，c为Sigmoid核函数的偏置系数。

2 融合实验分析

为验证文中算法有效性，采用两组遥感影像进行融合实验。第1组为武汉区Landsat 5的MS和SPOT 5的PAN影像。为方便分析，从影像中裁剪出空间信息和光谱信息较为丰富的区域进行实验，如图1，为方便分析，笔者在原图和融合结果图上都用方框表示出局部放大影像。具体实验步骤如下：

1)几何纠正：以PAN波段影像作为基准，选取20个控制点，对武汉市区的TM(除去TM6波段以外的6个波段)影像进行二次多项式内插法进行几何纠正，校正误差控制在1个像素以内。

3)利用Brovey算法对3个KPC进行归一化融合运算，最后得到融合影像。

图1 武汉地区融合实验数据Fig. 1 Fusion experimental data of Wuhan district

%

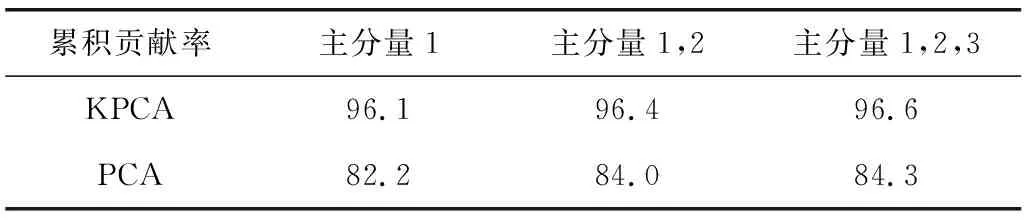
表2 KPCA与PCA算法累积贡献率比较(武汉区数据)Table 2 Comparison of cumulative contribution rate of KPCA and PCA (Wuhan data) %

采用PCA-Brovey和文中的方法对其做融合处理，所得到的融合结果如图2。从整体上看，两种算法在空间分辨和光谱分辨率上都有提高。从局部放大的结果看，如图2(c)、图2(d)，PCA-Brovey算法虽然算法简单快速，但是仅利用了84.3%的多光谱信息量，因此融合结果色调建筑区偏红，植被区偏绿，图像失真明显。KPCA-Brovey算法虽然耗时较长，但由于光谱信息利用率高且有利于非线性数据的挖掘，融合后光谱更真实，空间纹理更突出。

图2 PCA-Brovey和KPCA-Brovey融合实验结果(武汉地区)Fig. 2 Fusion experiment results of PCA-Brovey and KPCA-Brovey (Wuhan district)

第2组实验采用佛山市QuickBird 的MS和PAN波段数据(见图3)。实验步骤与武汉市数据融合相同，相关的实验表格见表3和表4。可以看出，利用KPCA算法前3个主分量的累积贡献率(96.1%)高于PCA算法(83.9%)。

表3 核函数与前3个核主成分累积贡献率的关系(佛山数据)Table 3 Relationship between kernel function and cumulative contribution rate of the first three kernel principal components(Foshan data) %

图3 佛山地区融合实验数据Fig. 3 Fusion experimental data of Foshan district

累积贡献率主分量1主分量1,2主分量1,2,3KPCA95.395.896.1PCA80.282.683.9

第2组数据所得的融合结果如图4。对比融合结果可知，图4(c)光谱失真严重，对比度较低，地物边界模糊。图4(d)明显优于图4(c)，图像的对比度较高，颜色接近原始多光谱影像，纹理信息丰富。

为了对这两种融合方法进行量化的比较和分析，笔者采用标准差、信息熵、相关系数和平均梯度这4种量化指标进行综合评价。量化指标的具体计算方法[20]如下：

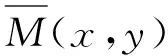
1)标准差

(11)

图4 佛山地区融合实验结果Fig. 4 Fusion experiment results of PCA-Brovey and KPCA-Brovey (Foshan district)

标准差反映了图像灰度基于灰度均值的离散程度，标准差越大，效果越好。

2)信息熵

根据信息论原理，1幅8bit影像x的信息熵为

(12)

式中：Pi为影像出现灰度值为i的像素的概率。H(x)反映了图像丰富程度，熵值越大，图像包含的信息量越丰富。

3)相关系数

融合影像和原始多光谱影像相关系数表示为

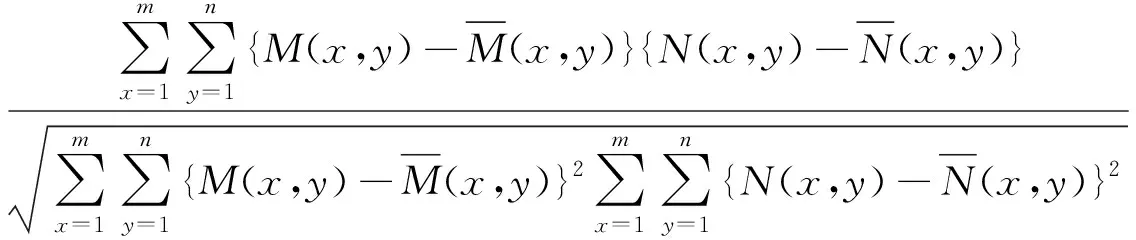
(13)

其中ρ反映融合影像和原始影像的相关程度，值越大，融合影像的光谱保真度越好。

4)平均梯度

(14)

其中ΔxM(x,y)=M(x,y)-M(x+1,y)，ΔyM(x,y)=M(x,y)-M(x,y+1)。

平均梯度反映地物微小细节的反差能力，其值越大，表示影像越清晰。

两组数据的融合结果指标见表5和表6。可以看出，总体上对于两组实验数据，KPCA-Brovey算法取得更好的评价指标，其融合结果光谱保真度和影像清晰度都占优。

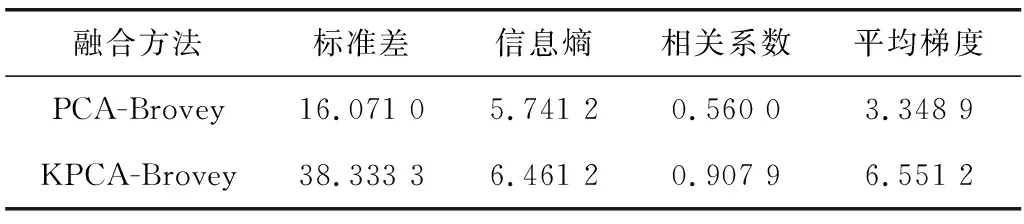
表5 两种方法融合质量指标比较(武汉区)Table 5 Comparison offusion quality indexes between two methods(Wuhan data)

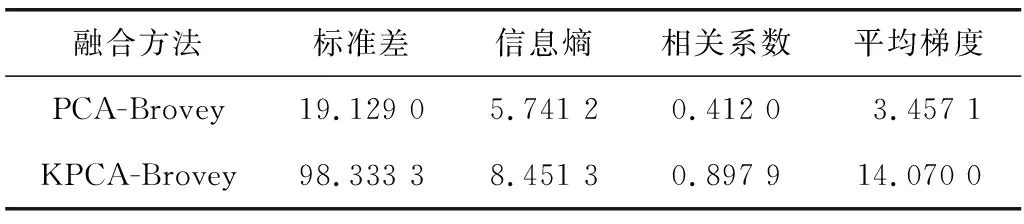
表6 两种方法融合质量指标比较(佛山区)Table 6 Comparison of fusion quality indexes between two methods(Foshan data)

3 结 论

基于KPCA特征提取方法不仅能够提高MS影像的光谱利用率，而且能够挖掘影像的非线性数据，降低光谱扭曲程度。Brovey算法简单、快速，能提高融合结果的空间分辨率。利用KPCA算法提取原MS影像的3个信息量最集中的主分量，再利用Brovey算法将PAN影像与主分量进行归一化融合运算，与PCA-Brovey算法进行比较，并对实验结果进行整理，分析，主要结论如下：

1)KPCA特征提取过程中，对于4种不同的核函数，高斯核函数的主分量累计贡献率最高，分别达到96.6%(武汉区)和96.1%(佛山区)，而PCA对应的贡献率为84.3%(武汉区)和83.9%(佛山区)，因此KPCA的光谱提取率明显高于PCA算法。

2)从目视判读上看，对于两组实验数据，无论是整体效果还局部影像，与PCA-Brovey方法比较，KPCA-Brovey融合结果中各地物(植被、建筑物和水)色调与原始多光谱影像更接近，地物(农田和道路)的细节更清晰。

3)从4种量化的融合评定指标看，对于两组实验数据， KPCA-Brovey融合影像的标准差，信息熵和平均梯度都高于PCA-Brovey算法，即提出方法的融合结果空间信息更丰富，影像细节更突出；光谱相关系数分别为0.907 9(武汉区)和0.897 9(佛山区)，明显高于PCA-Brovey算法(分别为0.560 0和0.412 0)，即提出的算法能够更好地保持原多光谱影像的光谱信息。

4)融合效率上，由于KPCA引入核函数参与计算，导致融合所需时间变长，而且算法对核参数的选择敏感，这些是后续需要进一步研究改进的地方。