民机四维航迹/姿态一体化自适应控制

樊垚，邵兴悦，李清东，任章

1. 中国船舶工业系统工程研究院 信息系统研究所，北京 100094 2. 北京机电工程总体设计部，北京 100854 3. 北京航空航天大学 自动化科学与电气工程学院，北京 100083

为了满足高速发展的航空运输需求，提高空域资源使用率，国际民航组织(ICAO)提出了新航行系统(FANS)的概念。新航行系统的核心组成部分是“基于性能导航(PBN)”的新型运行模式，该模式以改进航空系统效率、降低航空运营成本、提高航空运行安全性和空域使用率为目标，将航空机载设备、导航以及先进飞行控制技术紧密结合起来，为民航飞机运行的所有阶段提供更加精确、安全的飞行方法。

民机在航路终端区的起飞/着陆阶段是对其导航、引导和控制性能要求最高的航段，在此航段通常要求系统支持RNP-0.3甚至更为严格的规范，由于导航性能可以得到地面设备的有效支持，导航信息精度很高，此时飞行技术误差(FTE)是系统总误差(TSE)的主要部分。

飞行控制的本质是一类欠驱动控制问题。传统的飞控系统采用由内向外的串级控制设计思想，外环慢变回路的动态特性受内环回路特性的制约较为严重，飞机起飞/着陆阶段对飞机航迹控制要求很高，采取串级控制方法设计的航迹控制器动态响应慢，影响航迹控制精度。因此，必须采用引导控制一体化设计思想进行飞机四维航迹控制器设计，降低系统保守性，提高航迹响应动态和控制精度。

随着计算机技术和控制理论的发展，通过自动驾驶仪和自动油门综合等方法现已实现飞机飞控/推力一体化设计[1-3]，提高了系统的自动化能力，减小了飞行员的操纵负担。飞控/推力一体化控制技术主要解决飞机姿态与飞行速度的动力学耦合问题，不能从本质上降低串级飞控系统在航迹跟踪控制设计上的保守性。Williams等提出一种导引控制一体化设计思想，并将其应用于导弹制导控制系统的设计[4]，根据弹目相对运动信息，直接产生导弹气动舵面偏角控制指令，能够充分发挥导弹的动力学能力，提高导弹制导回路的响应速度。结合目标加速度测量与估计技术，基于滑模变结构控制理论可以完成飞行器导引控制一体化设计[5-6]。通过使用神经网络估计系统不确定性和误差，基于反步法能够实现飞行器导引控制一体化控制的目的[7-9]。通过结合线性二次型最优控制理论，使用反馈线性化方法也可以构建飞行器一体化飞行控制系统[10-12]。引入指令滤波器，采用自适应反演控制器实现无人机自主着舰横侧向控制[13]。当前，一体化飞行控制技术研究主要解决飞行器引导与控制回路动力学特性匹配的问题，针对航迹跟踪和到达时间高精度要求的研究工作尚未广泛开展。因此，为了有效解决民机航路终端区高精度航迹跟踪控制问题，应在充分借鉴现有一体化飞控系统设计思想的基础上，开展四维航迹/姿态一体化控制技术研究。

此外，飞机飞行在一个变化的大气环境中，机身各部分受到的空气动力不同，在起飞离场和进近着陆阶段飞机速度较低，这种效应更加显著。对于飞行控制系统而言，这种效应可以理解为飞机动力学系数的不确定性。由于地面效应的影响，地表附近产生大气扰动通过飞机航迹控制器间接产生的飞行技术误差是起飞离场和进近着陆阶段的主要误差因素之一。引入自适应算法是增强飞行器控制系统鲁棒性的有效途径，采用基于图像的导弹/无人机自适应末制导律可以消除目标尺寸、弹目相对距离和图像传感器引起的不确定性影响[14-16]，自适应飞行控制律也被用于解决扰动过程作用下飞机姿态控制问题，有效地改善飞行品质[17]。

本文基于LQG/LTR(Linear Quadratic Gaussian/ Loop Transfer Recovery)控制技术提出一种自适应四维航迹/姿态一体化控制方法。该控制方法以LQG方法为基础，利用LTR技术实现状态估计器和反馈控制器参数的匹配，在此基础上，引入基于自适应投影算子来补偿系统匹配不确定性，解决动力学系数不确定条件下的飞机航迹精确控制问题。

1 飞机动力学与环境特性模型

1.1 纵向航迹/姿态线性动力学模型

为了实现引导控制一体化设计思想，设计控制律所需的数学模型应精确地反映飞机空间六自由度运动，而不能将质心运动与绕质心转动分开考虑，忽略其相互影响。基于小扰动假设，建立了飞机线性化动力学模型[18-19]，并将其分解为纵向和横侧向运动两个部分，飞机纵向小扰动线性化方程组标准矩阵形式为

(1)

式中：Δ表征基准状态变量的扰动量；状态矢量xv包含的状态变量为纵向位移xg、高度zg、航迹速度VK、航迹速度迎角αK、俯仰角速率q和俯仰角θ的基准状态扰动量；控制矢量uv包含的控制变量为油门开度δf和升降舵偏δe的基准状态扰动量。

式中：

其中：m为飞机质量；Iy为飞机绕y轴转动惯量；V0为飞机基准速度；γ0为飞机基准航迹倾角；α0为飞机基准迎角；σ为发动机安装角；Te为推力偏心距；采用“XY”的形式表示飞机各无因次的气动导数，L为升力；C为侧力；D为阻力；T为推力；Ld为滚转力矩；Md为俯仰力矩；Nd为偏航力矩；α为飞机迎角；V为飞机速度；q为俯仰角速度；g为重力加速度。

1.2 横侧向航迹/姿态线性动力学模型

以水平协调转弯飞行状态为基准状态，飞机横侧向小扰动线性化运动方程组标准矩阵形式为

(2)

式中：Δ表征基准状态变量的扰动量，状态矢量xh包含的状态变量为侧向位移yg、航迹速度侧滑角βK、滚转角速率p、偏航角速率r、滚转角φ和偏航角ψ的基准状态扰动量；控制矢量uh包含的控制变量分别为副翼偏角δa和方向舵偏角δr的基准状态扰动量。

式中：

式中：Ix为飞机绕x轴转动惯量；Iz为飞机绕z轴 转动惯量；Izx为飞机交叉惯性积；φ0为飞机基准滚转角；θ0为飞机基准俯仰角；采用“XY”的形式表示飞机各无因次的气动导数，β为飞机侧滑角；其他变量定义与纵向航迹/姿态线性动力学模型一致。

1.3 大气风场特性模型

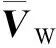
(3)

飞机受到的气动力和力矩取决于当前飞行状态，风速VW对空速VA和迎角α、侧滑角β等飞行状态都会产生影响。风场VW以及由风速沿机体的非均匀分布造成的风速梯度都能够使飞行状态相对无风情况发生偏移，引起附加气动力和力矩作用。因此，常值风的作用可以等效为气动参数的不确定性。此外，由于流体力学系统的非线性本质，必须把大气紊流作为随机过程进行处理,这里，采用Dryden模型描述大气紊流的尺度与强度[18]。

2 LQG/LTR控制方法及设计流程

线性高斯二次型(LQG)方法是解决随机线性系统最优控制问题的一种有效设计方法。随机系统的状态变量不能直接用于状态反馈，必须使用卡尔曼滤波方法对其进行估计，那么，最优控制问题与最优估计问题就需共同解决。LQG方法通过分别设计最优状态估计器和最优状态反馈控制律构成随机最优反馈控制系统。状态估计器和最优状态反馈控制律设计满足分离定理[20]。

典型线性系统的状态方程和输出方程为

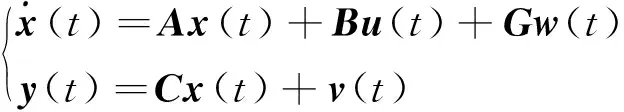
(4)

式中：x(t)∈Rn为状态向量；y(t)∈Rr为输出向量；u(t)∈Rm为控制向量；A∈Rn×n为状态矩阵；B∈Rn×m为控制矩阵；C∈Rr×n为输出矩阵；G∈Rn×p为过程噪声矩阵。实际系统的动态过程与测量输出均会受到噪声的影响，w(t)∈Rp为过程噪声，v(t)∈Rr为测量噪声，其协方差矩阵如下

式中：δ(t-τ)为Dirac函数。

图1为LQG控制器结构示意图，LQG控制器的传递函数矩阵为

K(s)=Kc(sI-A+BKc+KfC)-1Kf

控制器性能完全取决于控制增益矩阵Kc和Kf，定义随机性能指标J为

式中：Q为状态权值矩阵，Q=QT≥0；R为输出权值矩阵，R=RT>0。

随机线性调节器的最优状态反馈控制规律为

u(t)=-Kcx(t)

(5)

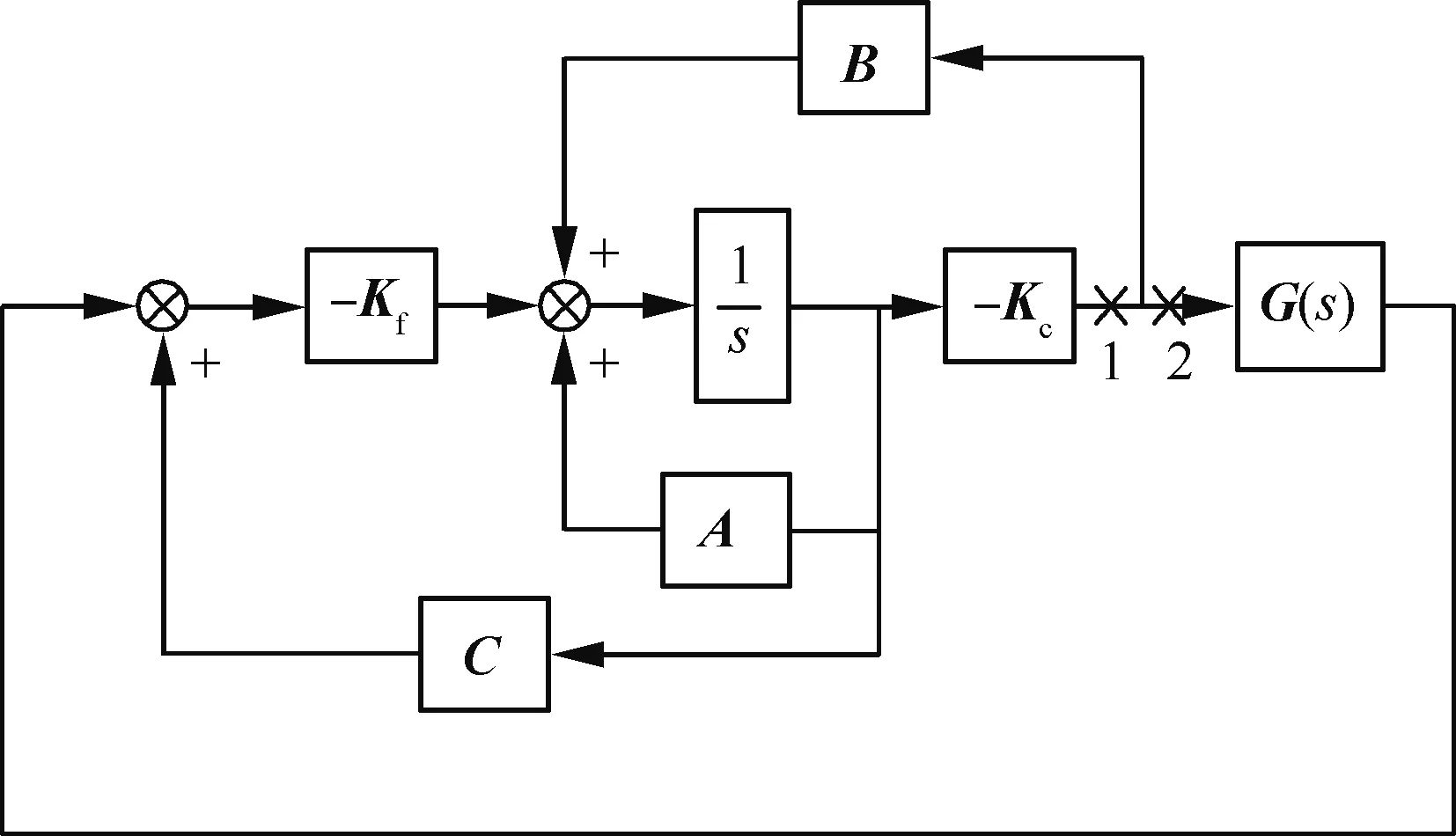
图1 LQG控制器结构示意图Fig.1 Schematic diagram of LQG controller structure

状态反馈增益矩阵Kc为

Kc=R-1BTPc

(6)

ATPc+PcA-PcBR-1BTPc+MQMT=0

(7)

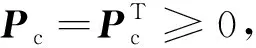
此外，当系统完全可控且完全可观时，线性系统的卡尔曼滤波器是渐近稳定的，稳态卡尔曼滤波器增益矩阵Kf为

Kf=PfCTV-1

(8)

PfAT+APf-PfCTV-1CPf+GWGT=0

(9)

对于LQG问题而言，系统控制输入信号u(t)的作用会影响到状态估计的效果，体现为过程噪声协方差矩阵W增加了与控制变量有关的部分，如式(10)所示。将Γ作为新的输入噪声标准差向量，利用式(9)设计卡尔曼滤波器。

ΓΓT=GWGT+q2BBT

(10)

式中：q为卡尔曼滤波器调节参数。

当在LQG控制回路中引入卡尔曼滤波器后，控制器参数的不合理选择将导致系统稳定裕度下降[21]。因此，LQG控制器设计的核心问题是协调设计最优反馈控制矩阵Kc和卡尔曼滤波矩阵Kf以同时保证系统的性能和鲁棒性。LQG/LTR方法的核心思想是设计理想的补偿控制器使得系统开环频率特性能够在系统关注的频率范围内逼近动态性能良好的预设目标回路[22-23]。首先需要根据指标要求设计具有良好动态性能和鲁棒稳定性的最优状态调节器回比函数，随后设计最优卡尔曼滤波器，使得输出端回比函数能够在一个足够大的频域范围内恢复预先设计的回比函数。当式(10)中q→∞时，系统输出端的回比函数可以实现有效恢复，逼近期望回路特性[22]，即图1中断开点为2时的回比函数趋近于断开点为1时的回比函数。

3 四维航迹/姿态一体化控制器设计

3.1 控制器构型选择

非均匀风场流过飞机时，机身各处受到气流作用不同，因此各部分产生的气动力也不相同，从控制系统设计的角度而言，这种现象可以理解为一种系统参数不确定性。鲁棒控制理论通常适用于参数不确定系统的控制器设计，Zhou和Ren基于Youla参数化分解理论[24]，提出了一种新型鲁棒控制器构型，如图2所示，鲁棒控制器K由M，N，U，V，Q这5部分实现。

定理1[24]已知被控对象P的标称模型为P0，P0的左互质分解为P0=M-1N，K0为能稳定标称模型P0的一个标称控制器，K0的左互质分解为K0=V-1U，则所有能稳定被控对象P的控制器K能表示为

K=(V-QN)-1(U+QM)

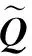
将上述新型鲁棒控制器构型应用于实际系统设计，控制器设计分为两部分，一部分是以跟踪误差为输入的主控制器，主要考虑系统的性能；另一部分是以系统估计误差为输入的补偿控制器，主要考虑对不确定性和干扰的补偿，韩京清提出了自抗扰控制理论，采用扩张状态观测器估计补偿系统不确定性和外部扰动[25]，可以通过合理设计输出误差校正函数或采用线性/非线性切换控制方法实时估计系统不确定性和外部扰动[25-27]，使得扩张状态观测量逼近系统真实存在的不确定性和扰动值。

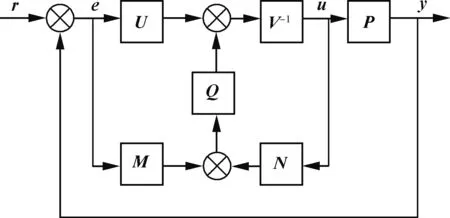
图2 基于Youla参数化方法的鲁棒控制器构型Fig.2 Youla parameterization roubst controller structure

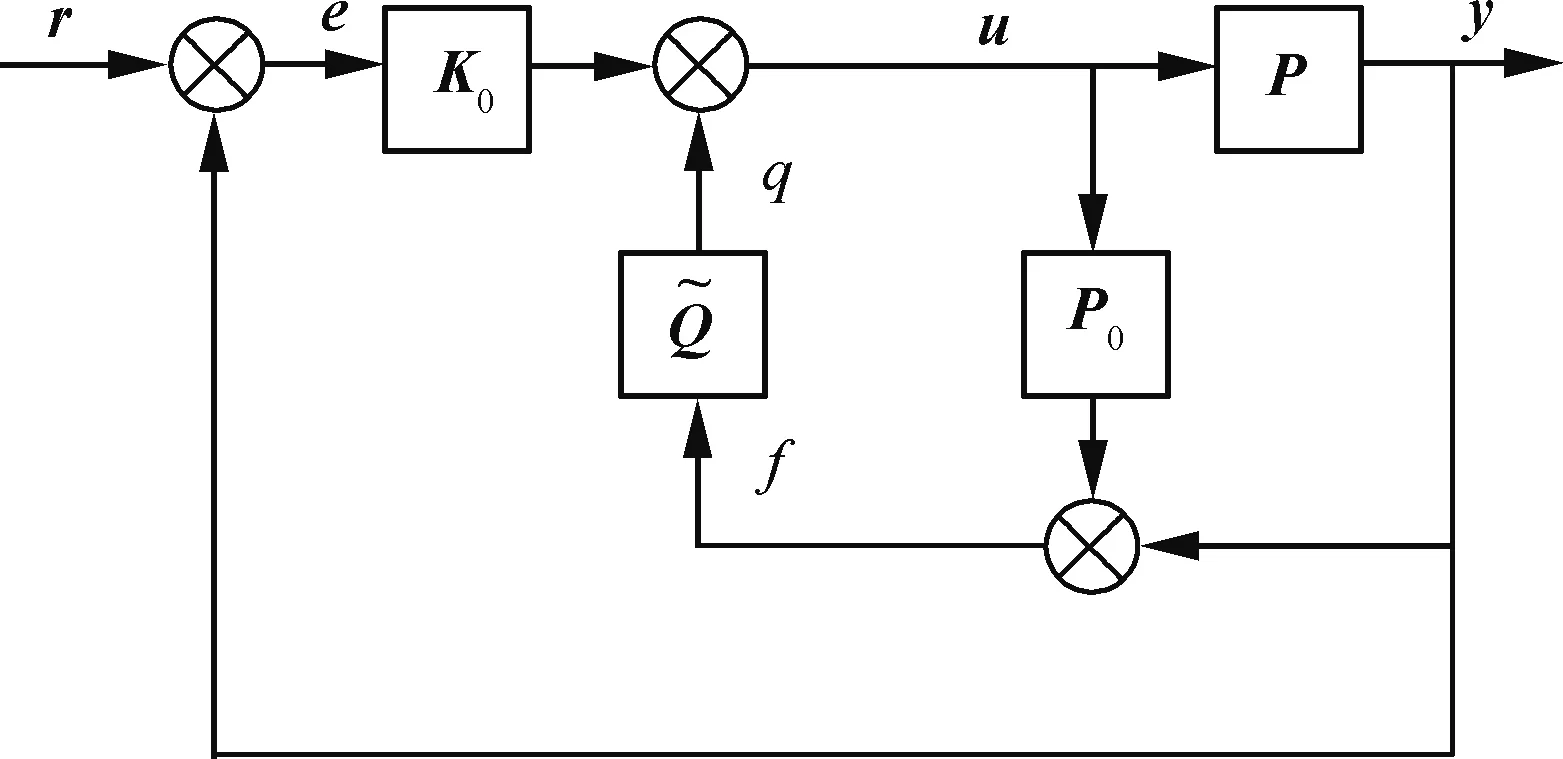
图3 新型鲁棒控制器构型Fig.3 Improved robust controller structure

采用新型鲁棒控制器构型和自抗扰控制技术能够兼顾系统的控制性能和鲁棒性，比较适用于飞行控制这类高可靠性和安全性要求的系统，但是由于民机飞行控制系统基本工作在飞行状态平衡点附近，航迹/姿态一体化控制器设计的目标是为了实现系统稳定，消除状态偏差，改善动态特性。因此，考虑到气动参数不确定性对飞行控制系统的影响，提出一种基于LQG/LTR技术的自适应控制器构型，如图4所示，该构型在前述鲁棒控制构型的基础上，不引入观测器实时估计系统不确定性与干扰，而采用自适应控制技术生成补偿控制量ucf抑制不确定性对系统性能的影响，因此，能够简化飞行控制律结构，降低工程实现复杂性，进而提高飞行控制系统可靠性。

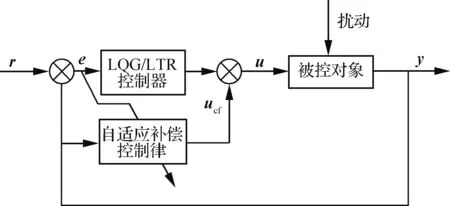
图4 基于LQG/LTR技术的自适应控制器构型Fig.4 Adaptive controller structure based on LQG/LTR

3.2 基于LQG/LTR的自适应控制方法

引入平滑投影算子[28]设计自适应控制律。定义参数矩阵Θ为

定义光滑凸函数集F(Θ)为

参数向量Θi的有界范数极值Θmax>0，0<ε<1。

定义Ωci为带有平滑边界的凸紧集：

定义矩阵投影算子proj(Θ,Y)为

proj(Θ,Y)=

proj(Θi,Yi)=

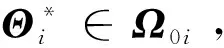
Ω0i={Θi∈Rn|fi(Θi)≤0}

(11)

(12)

那么，对于所有的t≥t0，参数向量Θi(t)满足

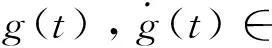
引理3系统式(4)同时采用反馈控制增益式(6)和卡尔曼滤波增益式(8)可以保证系统闭环状态矩阵Ae是Hurwitz稳定，且存在正定矩阵Qe使得下式成立。

式中：

当系统存在输入不确定性时，系统式(4)可表示为

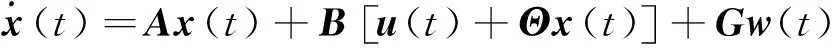
(13)

为了抑制不确定性对系统的影响，引入自适应反馈控制律为

(14)

系统状态方程可重新列写为

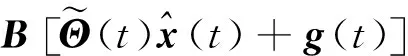
(15)

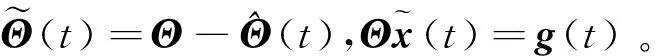
此外，系统状态估计器方程为

(16)

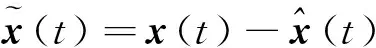
因此，系统状态变量估计误差方程为

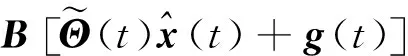
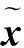
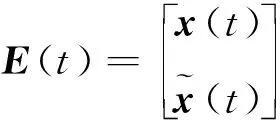
关于E(t)的状态方程为

(17)

定理2采用状态估计器式(16)，自适应反馈控制律式(14)和自适应律式(18)可以保证广义状态误差系统式(17)一致最终有界，广义误差向量E(t)收敛于Ω，如式(19)。如果不考虑系统噪声，即，w(t)=0且v(t)=0时，E(t)渐近收敛于0。

(18)

(19)

Ω0=4k2λmin(Qe)-4k4Θmax-

式中：λmin(Qe)为Qe的最小特征值；k为任意正实数。

证明：定义Lyapunov函数为

ET(t)PeBe1w(t)+ET(t)PeBe2v(t)+

根据引理1，可得：

由于向量g(t)的范数存在如下关系

gT(t)g(t)≤ΘmaxET(t)E(t)

(20)

根据式(20)及引理3，可得

(-λmin(Qe)+k2Θmax+

ET(t)E(t)+k2[wT(t)w(t)+vT(t)v(t)]

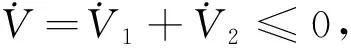
当不考虑系统噪声时，即认为w(t)=0且v(t)=0，有如下不等式成立

ET(t)E(t)dt≤

因此，E(t)∈2。由引理3可知Ae为Hurwitz稳定，那么，根据状态方程式(17)可知，∞。根据引理2，状态向量误差E(t)渐近收敛于0，即

E(t)→0,t→∞

证毕。

4 民机四维航迹/姿态一体化控制器设计

PBN运行模式下的民机飞行控制系统的设计目标是精确控制航迹，减小飞行技术误差，所以飞机纵向运动的被控变量为Δxg和Δzg，考虑到飞机侧滑转弯特性，飞机横侧向运动的被控变量为Δyg和ΔβK，那么，系统观测方程为

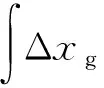
式中：

观测方程可重新表示为

式中：Ξ分别为v、h。基于自适应LQG/LTR方法的飞机四维航迹/姿态一体化控制器设计过程如下：

1) 期望最优调节器回路设计

根据式(5)～式(7)设计期望最优调节器回路作为标称控制器，满足系统性能要求。

2) 基于LTR技术的卡尔曼滤波器设计

根据式(8)～式(10)设计卡尔曼滤波器，通过合理选择参数在大频率范围内恢复回比函数。

3) 自适应反馈控制律设计

在标称控制器的基础上，根据自适应算子式(18) 和反馈控制律式(14)设计飞机四维航迹/姿态一体化自适应控制律。

5 仿真验证

以某型民机进近阶段典型工作点为例，分别设计纵向航迹/姿态一体化控制器和横侧向航迹/姿态一体化控制器，同时进行数字仿真以验证控制器性能，参考工作点状态如表1所示。

表1 民机典型工作点状态Table 1 States of operating point of civil aircraft

通过设定飞机纵向和横侧向航迹/姿态一体化控制器参数Q，R可得反馈增益矩阵Kc。通过设定飞机纵向和横侧向航迹/姿态一体化控制器卡尔曼滤波器参数W，q可得卡尔曼滤波器增益矩阵Kf。通过设定飞机纵向和横侧向控制参数矩阵G，并代入式(18)可解算系统自适应反馈控制量。

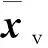
(21)

大气扰动对飞行控制的影响可认为是飞机气动系数存在乘性不确定性，如式(22)所示：

C=(1+0.3sint]C*

(22)

式中：C*为气动系数标称值；C为气动系数实际值。

图5～图7为存在大气扰动条件下飞机纵向位置误差、高度误差和侧向位置误差响应曲线，图8 为存在大气扰动条件下飞机侧滑角响应曲线。

由图可知，基于自适应投影算子的LQG/LTR控制器能够抑制较大气动参数不确定性对飞控系统的影响，验证了存在大气扰动条件下民机四维航迹/姿态一体化自适应控制方法的有效性。

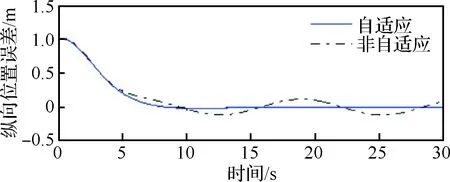
图5 存在大气扰动条件下纵向位置误差响应曲线Fig.5 Response curves of vertical position error under atmospheric disturbance conditions

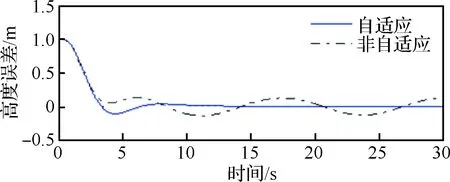
图6 存在大气扰动条件下高度误差响应曲线Fig.6 Response curves of height error under atmospheric disturbance conditions

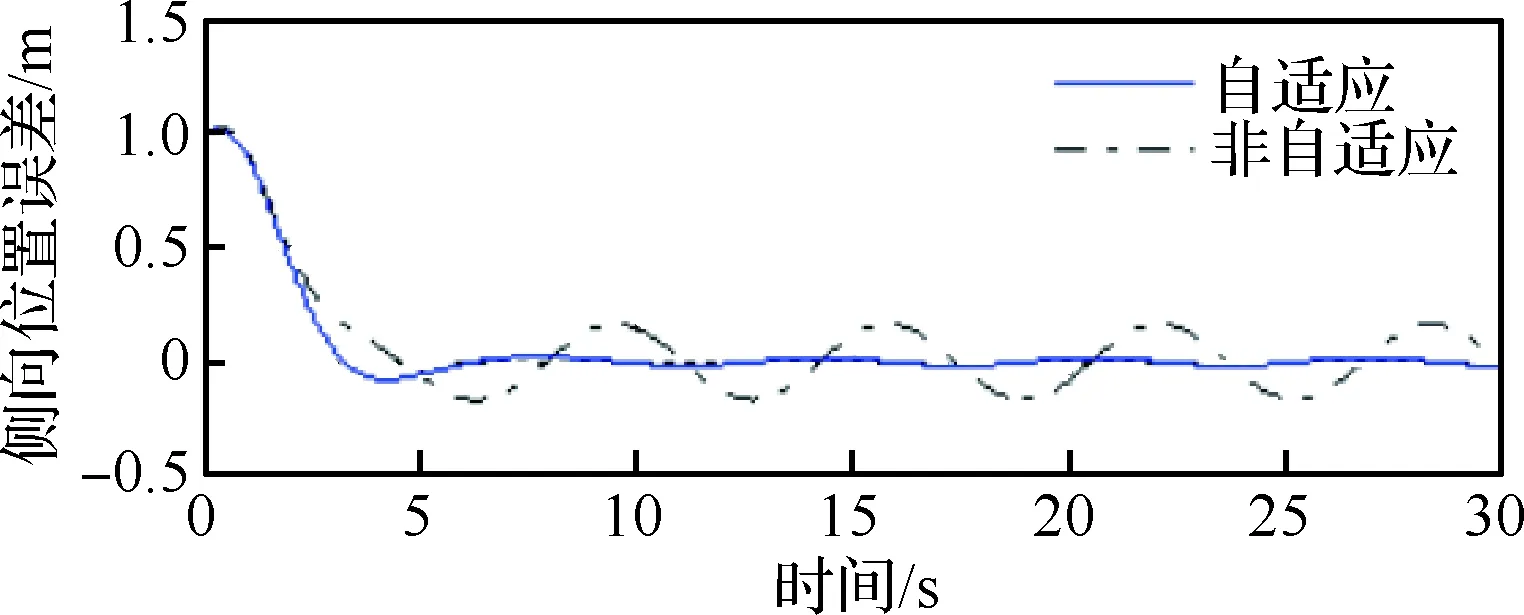
图7 存在大气扰动条件下侧向位置误差响应曲线Fig.7 Response curves of lateral position error under atmospheric disturbance conditions

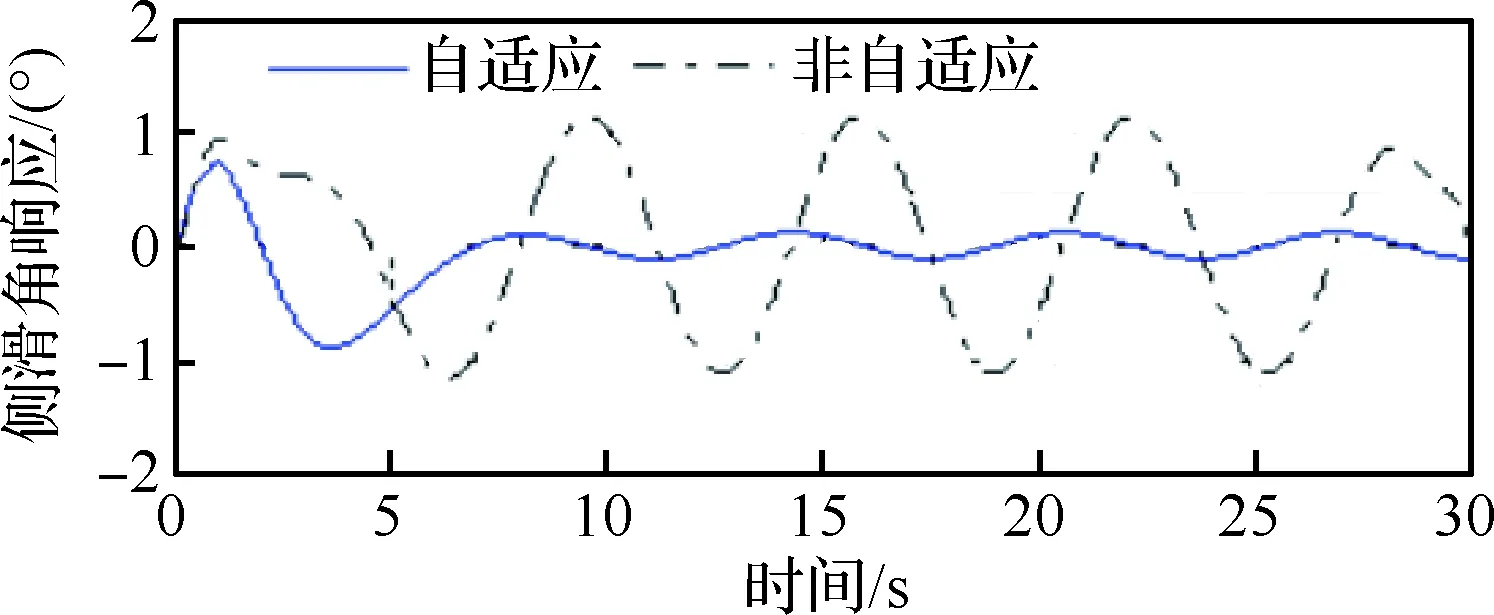
图8 存在大气扰动条件下侧滑角响应曲线Fig.8 Response curves of sideslip angle under atmospheric disturbance conditions

6 结 论

1) 基于LQG/LTR技术设计飞机四维航迹/姿态一体化控制器，实现状态估计器和反馈控制器参数匹配，解决随机多变量系统的综合问题。

2) 提出了基于投影算子的自适应控制方法，估计和补偿大气扰动引起的气动参数不确定性影响。

3) 基于自适应LQG/LTR控制方法的民机四维航迹/姿态一体化控制器，能够实现大气扰动作用下精确四维航迹跟踪，减少飞行技术误差。