插入式机翼下壁板对接附加弯矩研究
2019-03-04汤平李星
汤平,李星
1. 中国商飞上海飞机设计研究院 结构强度研究所,上海 201210 2. 中国商飞北京民用飞机技术研究中心 强度分析技术研究部,北京 102200
通常民用飞机的外翼中央翼对接有明确的工艺界面,在界面上布置对接肋[1]。对接肋组件是外翼中央翼的对接结构,根据对接形式的不同,相应的组件也不同。插入式下壁板对接结构的组件是“T”形下缘条和下对接带板,是一种较先进和成熟的对接形式[2]。在A350飞机、A380飞机和庞巴迪C系列飞机上都有运用,其特点是典型的双剪传力,传力直接,疲劳性能较好[3]。但对接区结构变化较大:蒙皮加厚、长桁端头加宽加厚、长桁腹板在端头切除一段再斜削,因此下壁板从等直段到对接段的中心线变化较大,受力时在对接区会形成附加弯矩。
A350飞机结构参考手册中对插入式下壁板对接的附加弯矩有所阐述,提出了削薄下壁板根部蒙皮以改变中心线走向的方法来减小附加弯矩,此方法缺点是增加蒙皮厚度余量、增加装配配合面、增加一道切削和处理的工序。国内朱森虎等对插入式下壁板对接中的长桁端头和下缘条开槽的细节参数进行了研究,其中长桁端头腹板的斜削部分设计考虑到减小附加弯矩的影响[4];杜兴刚等对插入式下壁板对接的下壁板和下缘条及对接带板的搭接区进行了分析,对对接区的传力和钉孔的损伤容限进行了分析研究[5]。但鲜见有直接研究插入式机翼下壁板对接附加弯矩的论述,同时目前先进民机的机翼下壁板都是复合材料,在对接区相对金属都更厚,中心线变化更明显,附加弯矩会更大,造成的不利也会更多。
因此,研究附加弯矩的形成,优化对接结构细节参数,以到达减小附加弯矩和其不利影响的目的。本文首次从改变外翼下壁板和中央翼下壁板相对位置的角度来研究附加弯矩的变化,提出在建立骨架模型时即优化中央翼下翼面外形面相对外翼下翼面位置来减小附加弯矩的方法,该方法的优点是不在相关结构的重量、装配和制造上增加不利点。
1 插入式下壁板对接
1.1 对接形式
插入式下壁板对接形式的主要特点是1号肋下缘条展向开槽,下壁板长桁腹板插入槽中;长桁端头的腹板切去一段,长桁的下部缘条加宽,1号肋下缘条和对接带板夹住蒙皮和长桁下部缘条。具体的结构形式见图1。
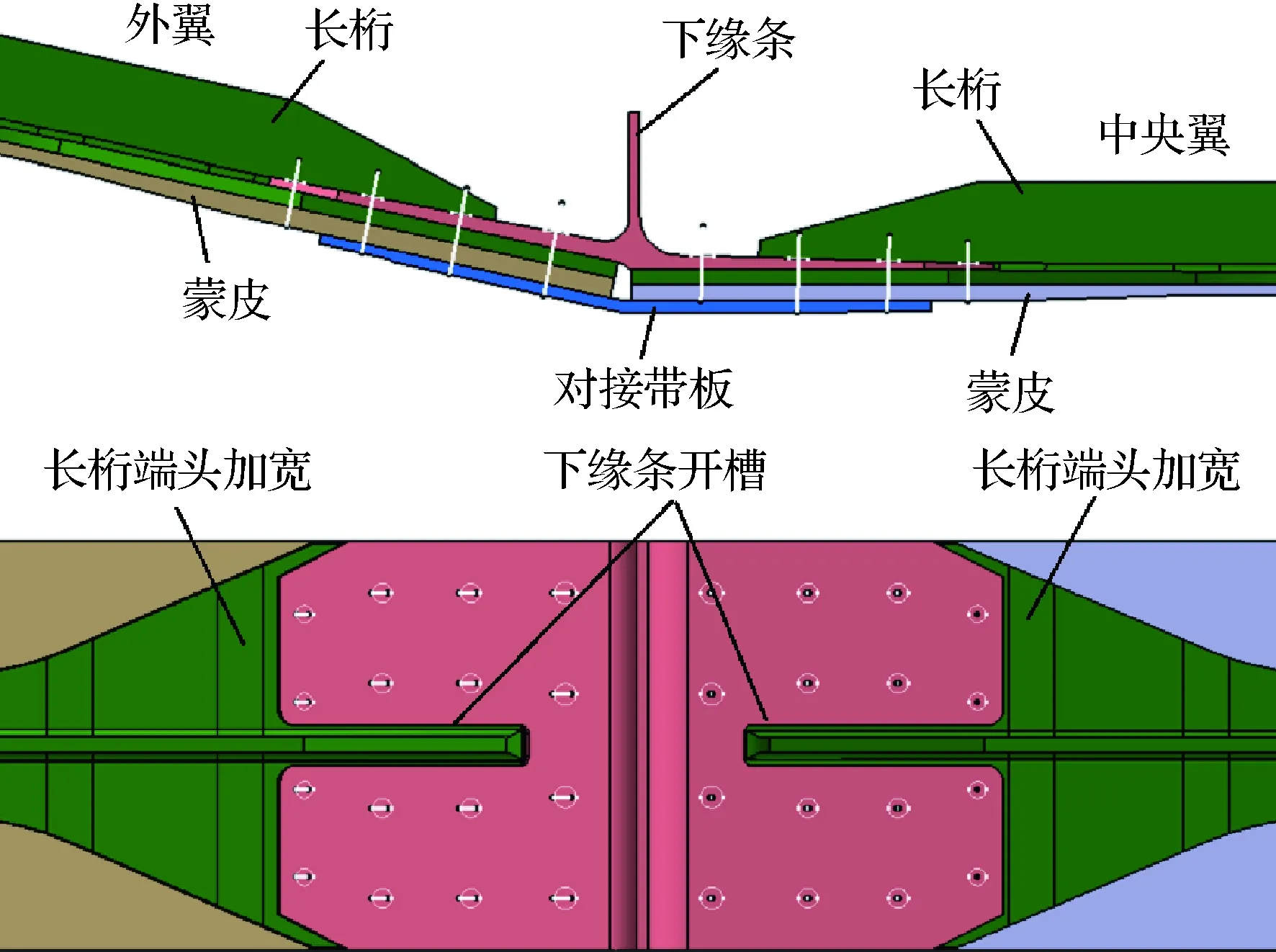
图1 插入式下壁板对接示意图Fig.1 Schematic of inserted lower panel butt-joint
图1中只显示了单长桁的下壁板,实际飞机机翼下壁板是多长桁,长桁端头加宽段并排,对缝间隙控制在5 mm以下。以下分析以单长桁典型对接结构为例。
1.2 偏 心
在下壁板的等直段,长桁和蒙皮的截面是完整连续的,中心线是一条直线;而在对接区,长桁的腹板切去一段并斜削,长桁的下缘条从过渡区到对接区加宽加厚;蒙皮也逐渐加厚。从等直段到对接区连接段,下壁板的中心线必然变化,产生偏心[6-7],见图2。
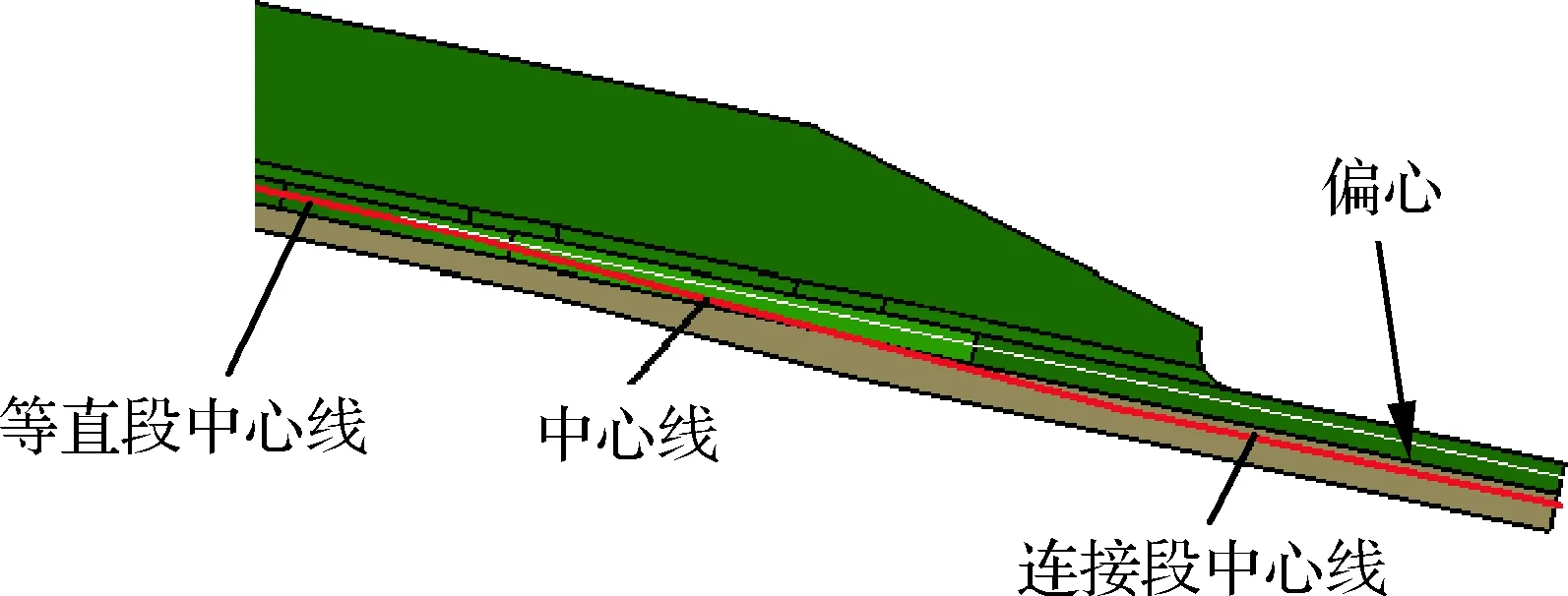
图2 下壁板偏心Fig.2 Lower panel eccentric
1.3 附加弯矩
外翼中央翼下壁板承受拉伸载荷,由于下壁板在对接区的偏心,下壁板上会产生附加弯矩。外翼拉伸载荷在对接肋腹板上会产生压力,肋腹板通常是整体加筋板[6-7],和下缘条的立板之间也有偏心,同样会产生弯矩,见图3。
图3中α为外翼上反角,腹板压力NR=NWsinα,NW为外翼远端载荷;中央翼侧拉力NCW=NWcosα。因此,外翼下壁板上局部的附加弯矩MW=-eWNW,eW为外翼下壁板中心线的偏心距;中央翼下壁板上的局部附加弯矩MCW=eCWNCW,eCW为中央翼下壁板中心线的偏心距;对接肋腹板上的局部附加弯矩MR=-eRNR,eR为1号肋偏心量。
肋腹板上的附加弯矩在肋腹板和上缘条连接、和下缘条连接的两处都有,且大小相等方向相反,相互平衡[8]。
在对接区,下壁板被下缘条和对接带板夹住并用螺栓连接,会形成4层材料对接区中心线。中央翼对接区中心线和下缘条立板中心线交于R点(定义为旋转中心(f)),外翼对接区中心线和R点会有偏心w(错位),此偏心会影响整个对接区的附加弯矩Mf。偏心和弯矩见图4。图4中w会形成顺时针弯矩,w取正值,若外翼对接区中心线在R点上方,w会形成逆时针弯矩,w取负值。
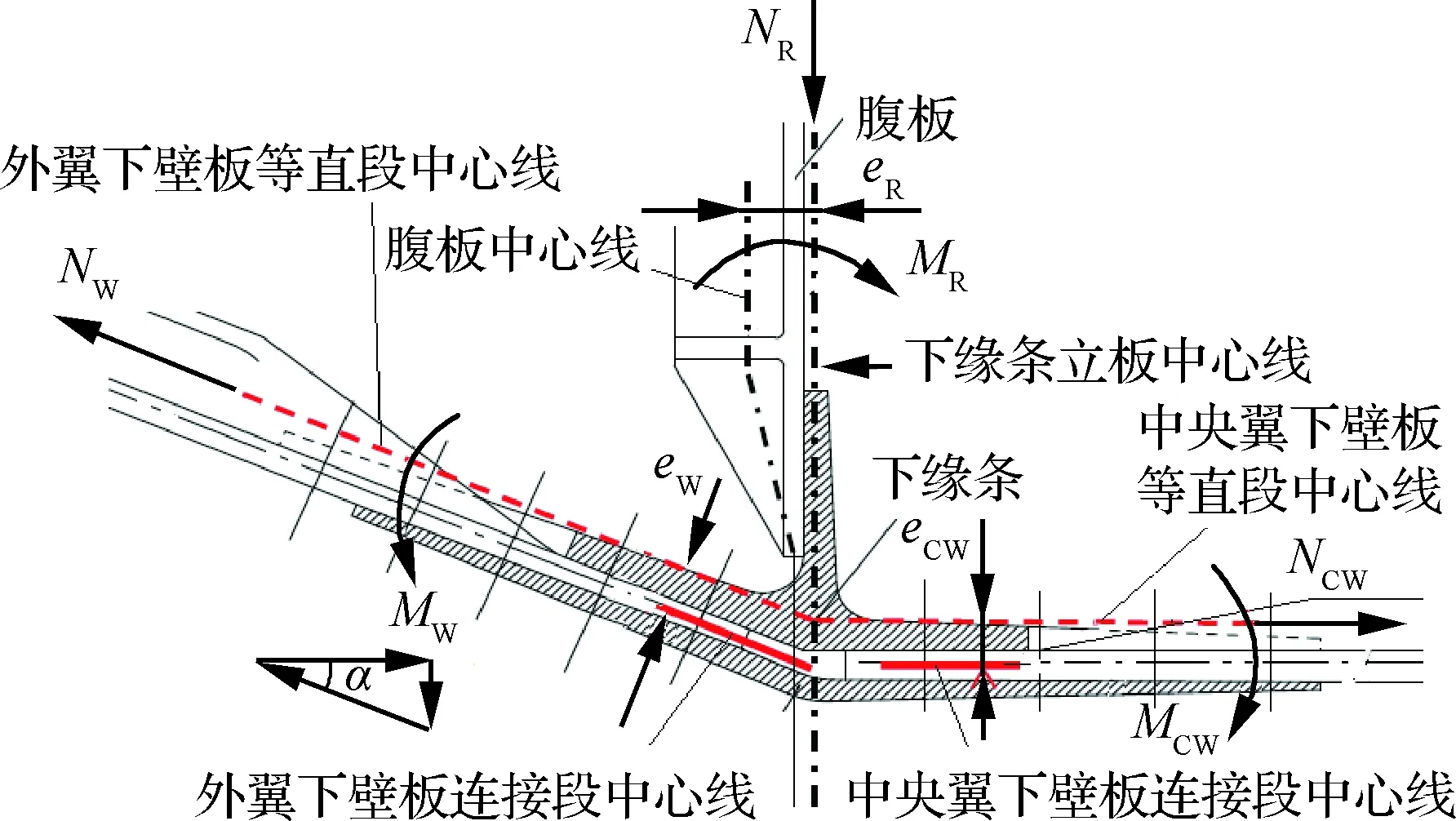
图3 下壁板对接区局部附加弯矩示意图Fig.3 Schematic of additional bending moment on lower panel butt-joint
图4 对接区偏心及弯矩示意图Fig.4 Schematic of eccentric and bending moment in butt-joint area
外翼对接区弯矩MWJ=-eWJNW,eWJ为外翼侧偏心量;中央翼对接区弯矩MCWJ=eCWJNCW,eCWJ为中央翼侧偏心量;外翼对接区相对中央翼对接区的弯矩MJ=wNW。
整个下壁板对接区,即从外翼等直段到中央翼等直段的弯矩:
Mf=MWJ+MCWJ+MJ=-eWJNW+eCWJNCW+
wNW=(-eWJ+eCWJcosα+w)NW=ΔNW
(1)
1.4 减小附加弯矩的方法
由Mf的表达式可知,Δ越小,对接区附加弯矩Mf越小。通常-eWJ+eCWJcosα为小负值,即w为一个小正值较好;但不能排除根据实际结构计算的-eWJ+eCWJcosα为正值,这时w为一个小负值较好。
本文提出一种减小机翼下壁板对接区附加弯矩的新方法:优化中央翼下翼面外形面相对外翼下翼面的位置,使得Mf表达式中的Δ最小化,从而减小附加弯矩Mf。
传统的中央翼下翼面外形面骨架是根据外翼下翼面外形面和1号肋平面的交线定义的,骨架模型构建的具体对接区结构会自然形成一个对接区偏心距w,Δ的值也可以计算出来。根据w的值和-eWJ+eCWJcosα的值,可以容易判断出如何优化:抬高或降低中央翼下翼面外形面。
弯矩Mf是外翼载荷向机身和中央翼传递中产生的内部载荷,需对接区结构及其相邻结构的内力来平衡[9],因此Mf是越小越好。
2 实例分析
实例分析采用工程计算方法。某A型飞机的机翼下壁板对接是典型的插入式,下缘条开槽,长桁腹板端头切除一段并斜削,外翼长桁为“工”形,中央翼长桁为“T”形。
2.1 附加弯矩分布计算
选取A型飞机靠近机翼后梁的一根长桁做分析,其部分尺寸及偏心值见图5。其中外翼下壁板蒙皮连接段厚度为12.95 mm,中央翼下壁板蒙皮连接段厚度为10.73 mm;偏心为w={(10.73-3.7-1.02) -[ (12.95-4.44-0.72)/cos 12.5°-3.5tan 12.5°]}cos 12.5°=-1.16 mm。
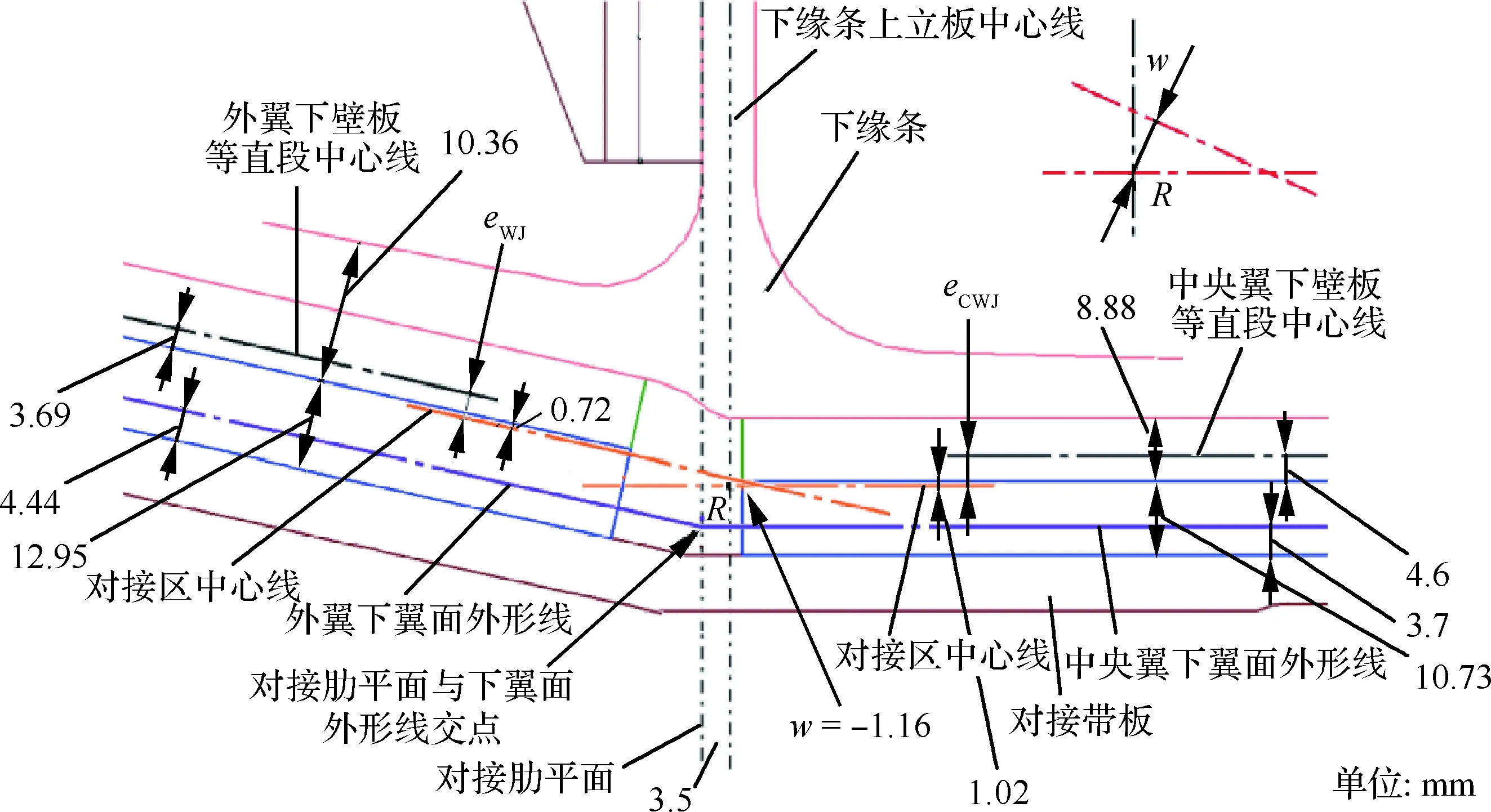
图5 下壁板对接结构偏心示意图Fig.5 Schematic of eccentric of lower panel butt-joint structure
外翼的2号肋对外翼下壁板提供支持;龙骨梁对中央翼下壁板提供支持;对称面对中央翼下壁板提供支持;对接肋腹板上部和上缘条连接,对腹板提供支持。
对接区是个超静定结构,其原结构见图6。图中:E为弹性模量;a1、a2和a分别为外翼下壁板等直段长度、对接段长度和总长度;Ia1和Ia2分别为a1和a2段的惯性矩,其余惯性矩变量定义同此处;b1、b2和b分别为中央翼下壁板等直段长度、对接段长度和总长度;c为龙骨梁支持位置到中央翼下壁板对称面位置的距离;h1、h2、h3和h分别为肋腹板高度、上缘条立板高度、下缘条立板高度和肋高度。
根据图6,相关尺寸及附加弯矩见表1。
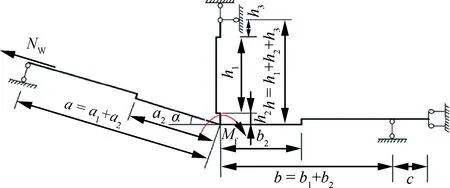
图6 对接区受力及支持示意图Fig.6 Schematic of load and support in butt-joint area表1 对接区几何尺寸Table 1 Geometry of docking area
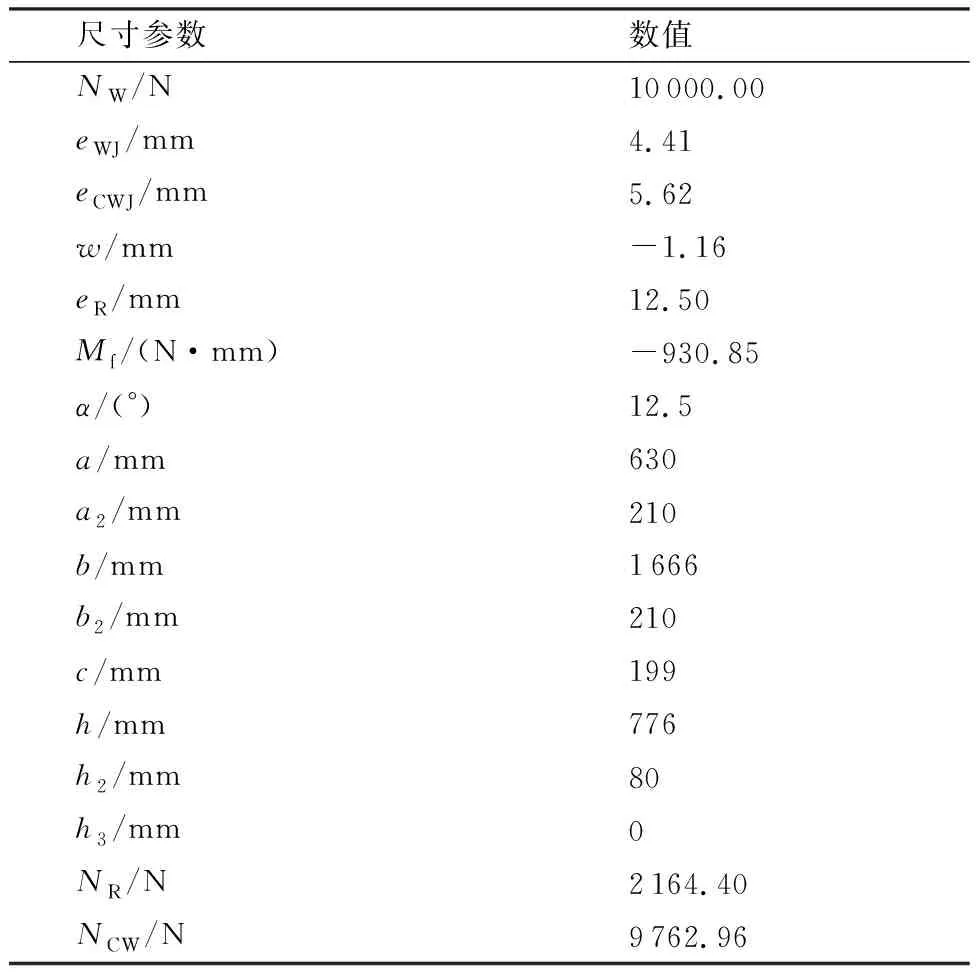
尺寸参数数值NW/N10000.00eWJ/mm4.41eCWJ/mm5.62w/mm-1.16eR/mm12.50Mf/(N·mm)-930.85α/(°)12.5a/mm630a2/mm210b/mm1666b2/mm210c/mm199h/mm776h2/mm80h3/mm0NR/N2164.40NCW/N9762.96
按NW=10 000.00 N分析,求得对接区附加弯矩Mf=-930.85 N·mm,腹板压力NR=2 164.40 N,中央翼壁板拉力NCW=9 762.96 N。
将图6中超定静结构中去掉多余约束后所得到的静定结构称为力法的基本结构[10],见图7。
基本结构是静定结构,在原有载荷和多余未知力共同作用下形成力法的基本体系[11],见图8。图中:A0、C0和D0分别为在原有载荷作用下的2号肋处支反力、龙骨梁处支反力和对称面处支反力。
根据基本体系中原有载荷和多余载荷X1、X2、X3分别计算支反力和弯矩,X1、X2按单位载荷(力)1、X3按单位载荷(弯矩)1计算。
原有载荷下的支反力和弯矩计算按方程式:
(2)
按计算结果绘制弯矩图,见图9。
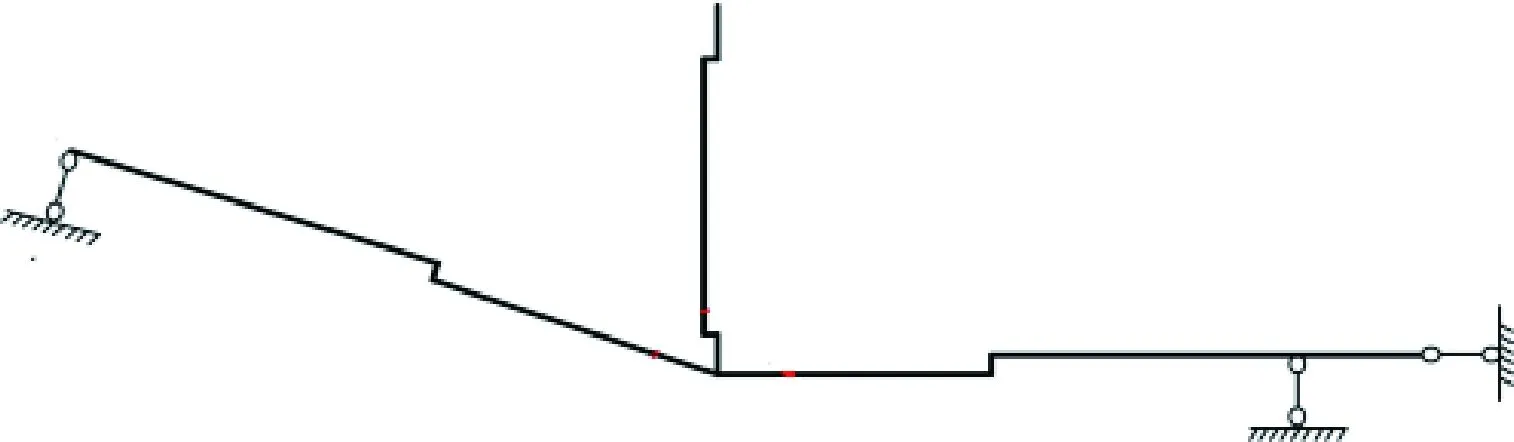
图7 对接区受力力法基本结构图Fig.7 Basic structure diagram of force method in butt-joint area
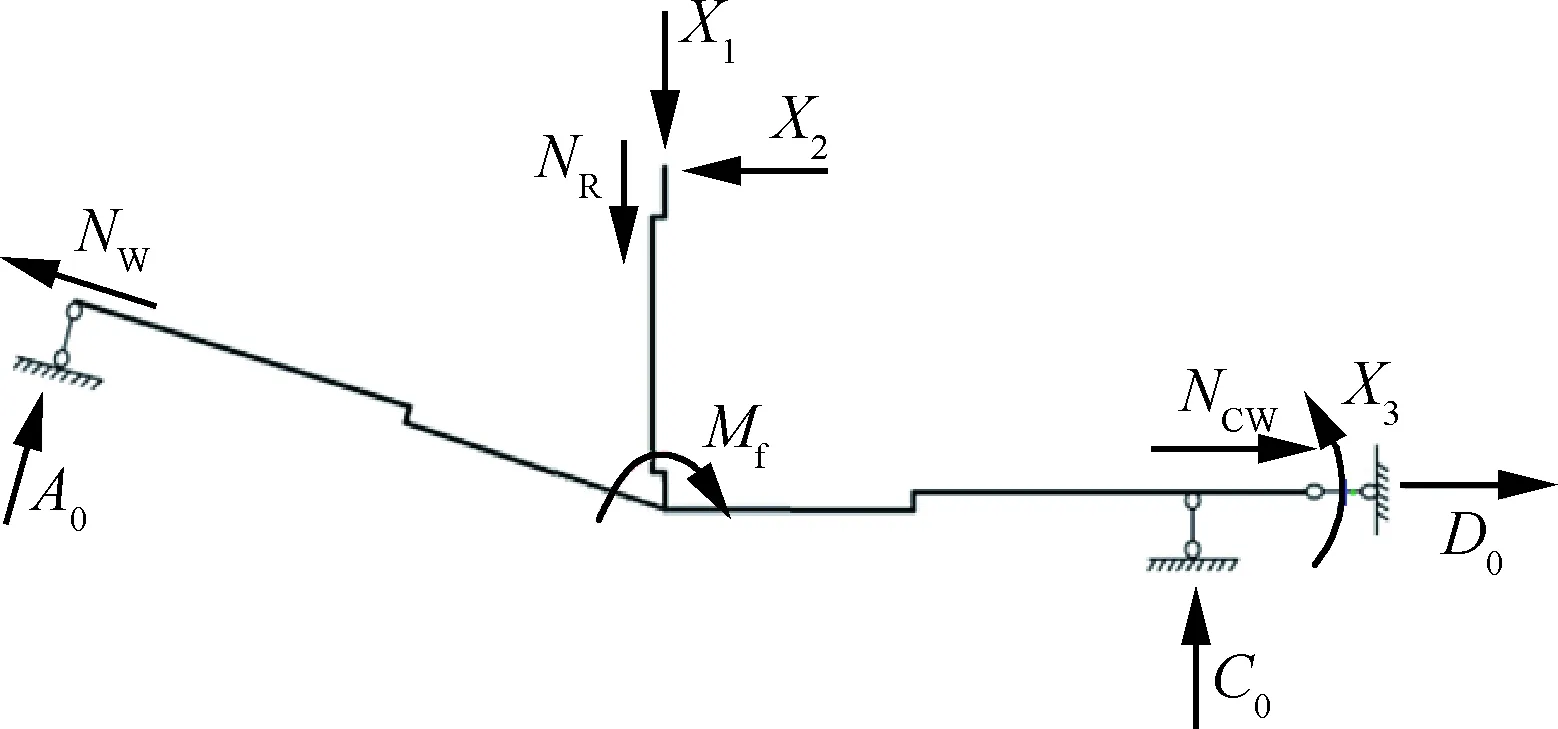
图8 对接区受力力法基本体系Fig.8 Basic system of force method in butt-joint area
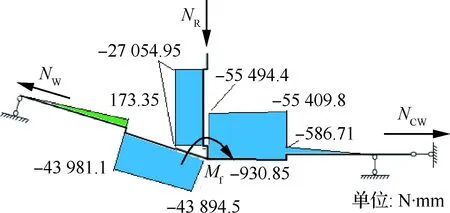
图9 按原有载荷计算结果Fig.9 Calculation results based on the original load
按单位载荷X1计算单位弯矩,其方程式见式(3),弯矩图见图10。
(3)
式中:A1、C1和D1分别为在多余载荷X1作用下的2号肋处单位支反力、龙骨梁处单位支反力和对称面处单位支反力。
按单位载荷X2计算单位弯矩,其方程式见式(4)。弯矩图见图11。
(4)
式中:A2、C2和D2分别为多余载荷X2作用下的2号肋处单位支反力、龙骨梁处单位支反力和对称面处单位支反力。
按单位载荷X3计算单位弯矩,其方程式见式(5)。弯矩图见图12。
(5)
式中:A3、C3和D3分别为在多余载荷X3作用下的2号肋处单位支反力、龙骨梁处单位支反力和对称面处单位支反力。
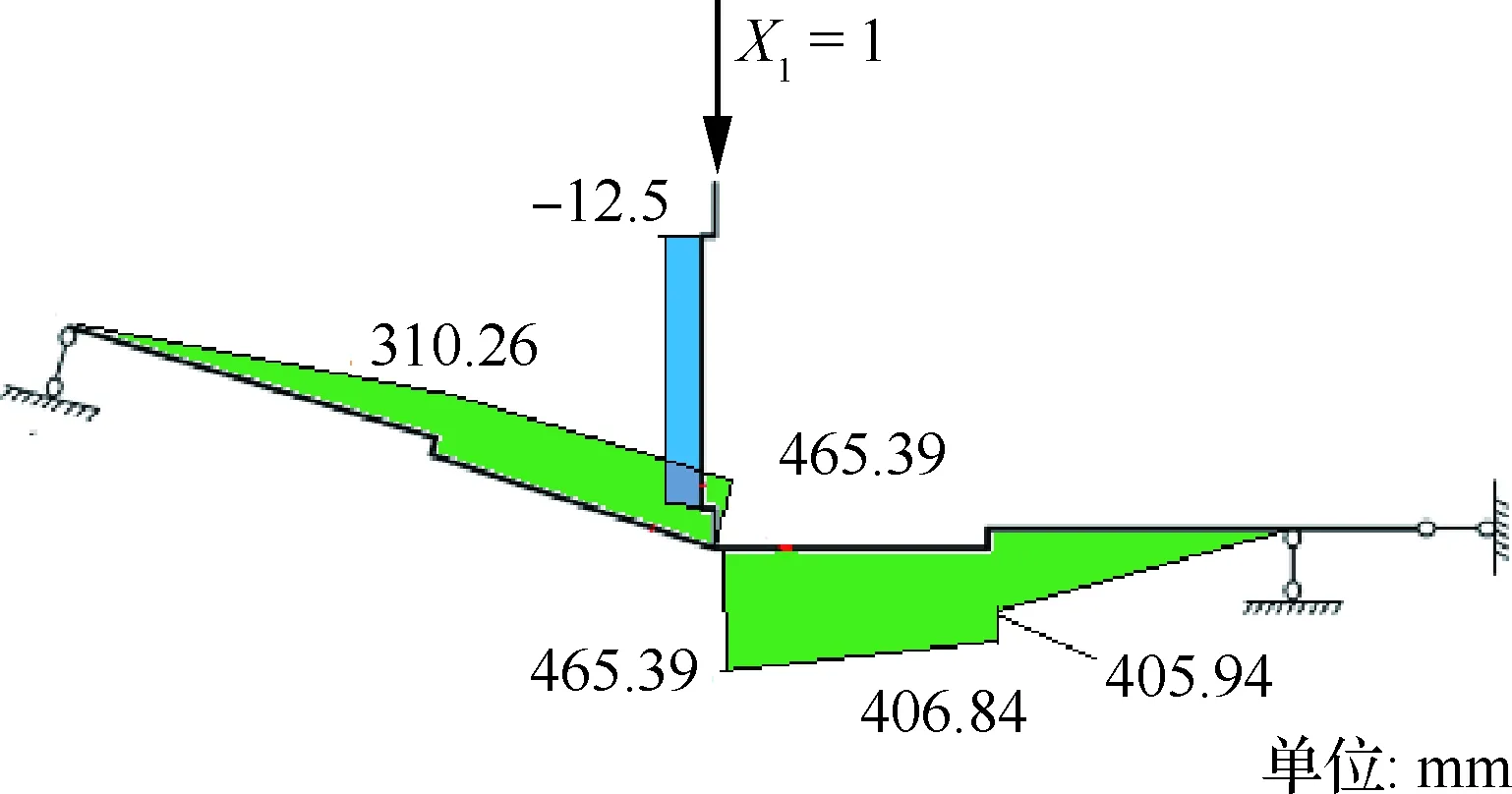
图10 加单位载荷X1计算结果Fig.10 Calculation results of unit load X1
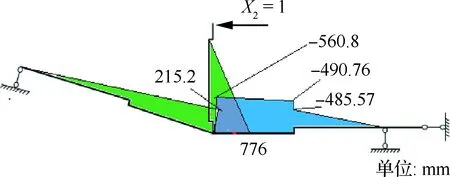
图11 加单位载荷X2计算结果Fig.11 Calculation results of unit load X2
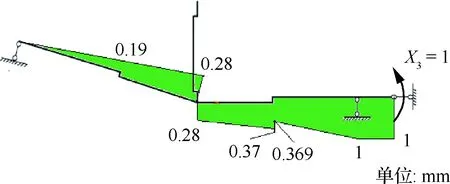
图12 加单位载荷X3计算结果Fig.12 Calculation results of unit load X3
根据力法计算超静定梁的方程[11]为
(6)
式中:Δ1、Δ2和Δ3分别为约束放开处在多余载荷和原载荷下的总位移;系数和自由项表达为
其中:Mi、Mj和MP分别为在Xi=1、Xj=1和原有载荷单独作用下基本结构中的弯矩;I为惯性矩。
A型飞机的下缘条和对接带板是钛合金,蒙皮和长桁是铝合金,将壁板近似为等刚度梁,根据弯矩图、下壁板的具体尺寸,用图乘法计算δii、δij、δji、ΔiP,计算过程(局部)见图13。
图乘法结果如下:δ11=3.057×10-3mm/N,δ22= 1.168×10-2mm/N,δ33=1.857×10-8mm/N,δ12=-2.579×10-3mm/N,δ13=4.310×10-6mm/N,δ23=-4.418×10-6mm/N。Δ1P=-1.460×10-1mm,Δ2P=-2.518×10-1mm,Δ3P=-1.126×10-4mm。
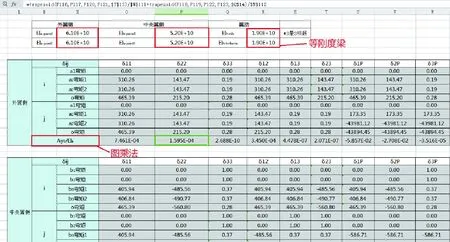
图13 图乘法计算系数Fig.13 Graph multiplication calculation coefficients
将δii、δij、δji、ΔiP代入超静定梁方程后计算,可求得多余载荷X1=87.78 N;X2=39.05 N;X3= -5 017.92 N;根据图9,再叠加图10~图12 后,总的弯矩分布见图14。
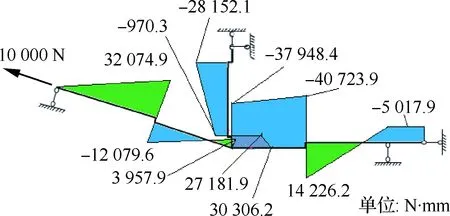
图14 对接区弯矩分布Fig.14 Bending moment distribution of butt-joint area
2.2 附加弯矩影响
将A型飞机机翼下壁板对接区结构划分出弯矩影响位置,见图15。
从图14的附加弯矩分布,可以看出中央翼一侧的下壁板靠近对接区,即图15中B、C、D所示位置,包括中央翼长桁腹板斜削区,附加弯矩为负值,有向下凹起的弯曲的趋势。在设计上需注意斜削根部的应力情况,尤其对于复合材料下壁板,需考虑防止长桁腹板分层和长桁缘条蒙皮间脱胶的问题[2];庞巴迪C系列飞机和波音787飞机在此处是采用在长桁缘条上打铆钉[11]防止脱胶。附加弯矩作用下对接区变形见图16。
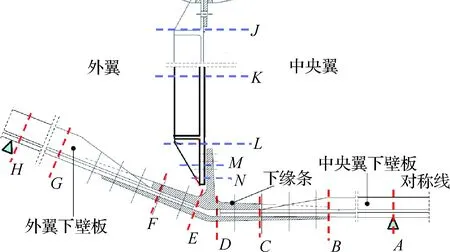
图15 某机型机翼下壁板对接区Fig.15 Butt-joint area at wing panel of one plane model
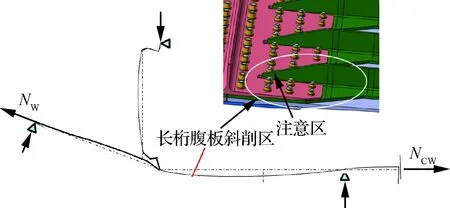
图16 附加弯矩作用下对接区变形Fig.16 Deformation of butt-joint aera zone under additional bending moment
图15中对接肋腹板和下缘条立板连接的M、N区也受到附加弯矩的影响。由于此处连接通常是单剪连接,腹板的连接边需适度加厚[12],紧固件也需选用抗拉螺栓。
3 模型分析
机翼下壁板对接接区有5条中心线:下缘条立板中心线、中央翼下壁板对接区中心线、中央翼下壁板等直段中心线、外翼下壁板对接区中心线、外翼下壁板等直段中心线。其中2条连接区中心线反映了外翼对接区结构和中央翼对接区结构的相对位置,不同的相对位置对应了不同的w和Δ,从而对应了不同的附加弯矩分布。
3.1 四组分析模型组件
照此思路,为有限元计算分析再建立4组插入式下壁板对接结构的模型作为分析组件,对接结构仍以2.1节分析的某A机型为例。4组组件分别为1型、2型、3型和4型。
2.1节分析的构型是骨架模型定义后自然形成的,为基本型(0型)。1型是在0型的基础上调整中央翼侧的结构位置,使得外翼对接区中心线相对R点的偏心距为w=0;其构型见图17。
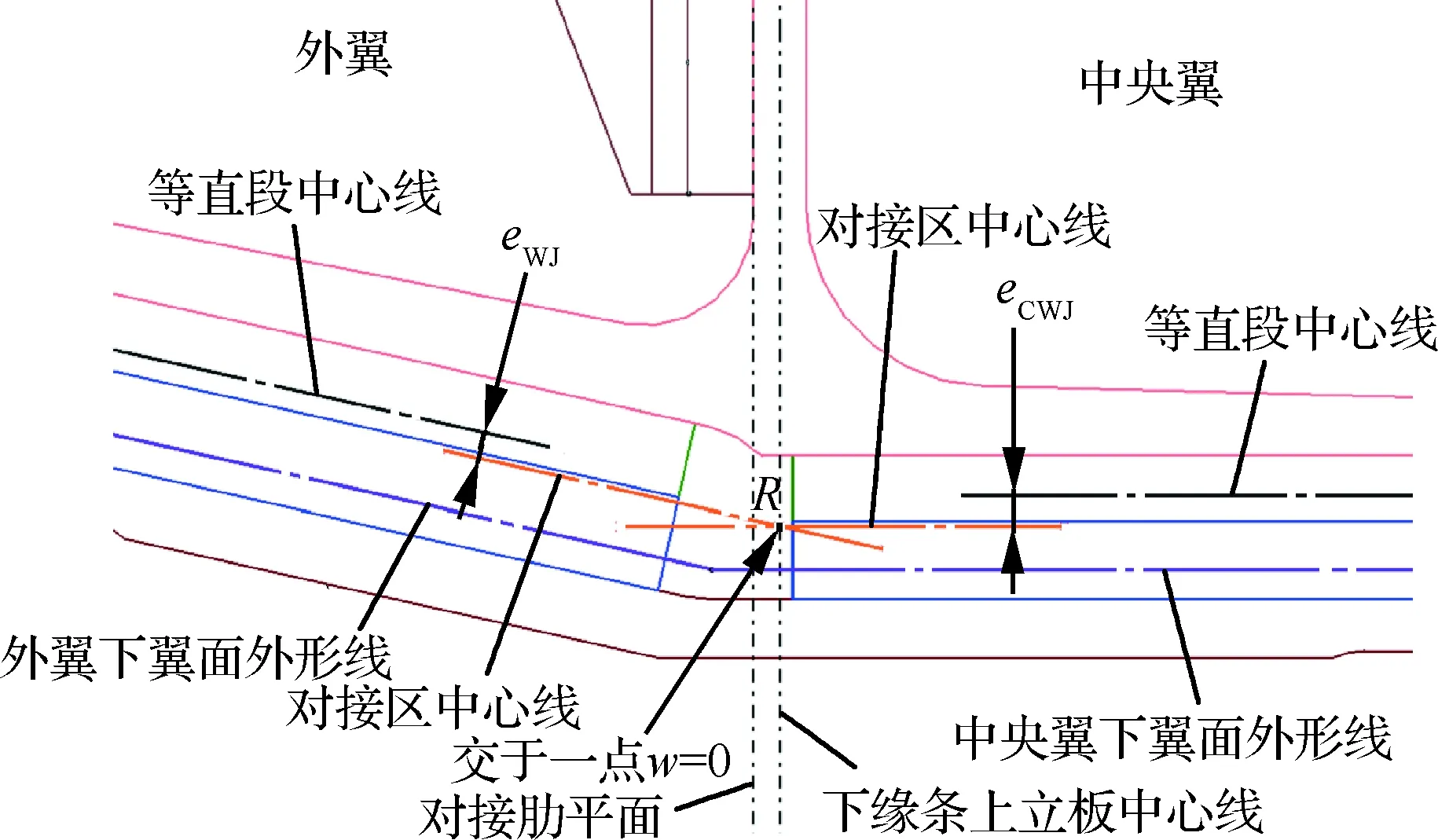
图17 1型对接组件偏心示意图Fig.17 Schematic of eccentric of No.1 butt-joint component
2型是在1型的基础上中央翼侧的结构继续抬高,使得外翼对接区中心线、中央翼对接区中心线和1号肋平面三者交于一点,此时偏心距为w= 3.5sin 12.5°=0.76 mm;其构型见图18。
3型是在2型基础上将中央翼侧结构继续上抬,使得w=3 mm,其构型类似2型,见图19。
4型是在1型(w=0)基础上将中央翼侧结构下降,使得w=-3 mm,见图20。
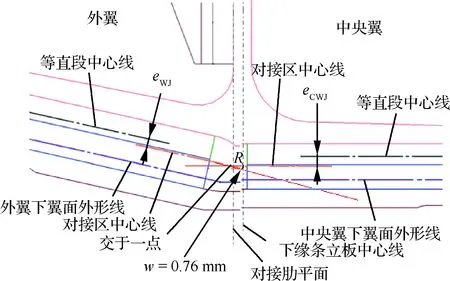
图18 2型对接组件偏心示意图Fig.18 Schematic of eccentric of No.2 butt-joint component
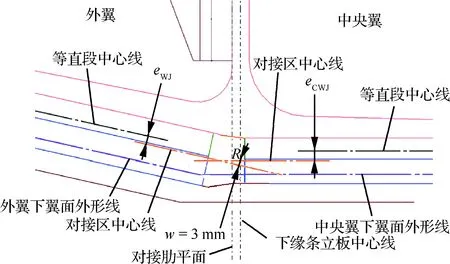
图19 3型对接组件偏心示意图Fig.19 Schematic of eccentric of No.3 butt-joint component
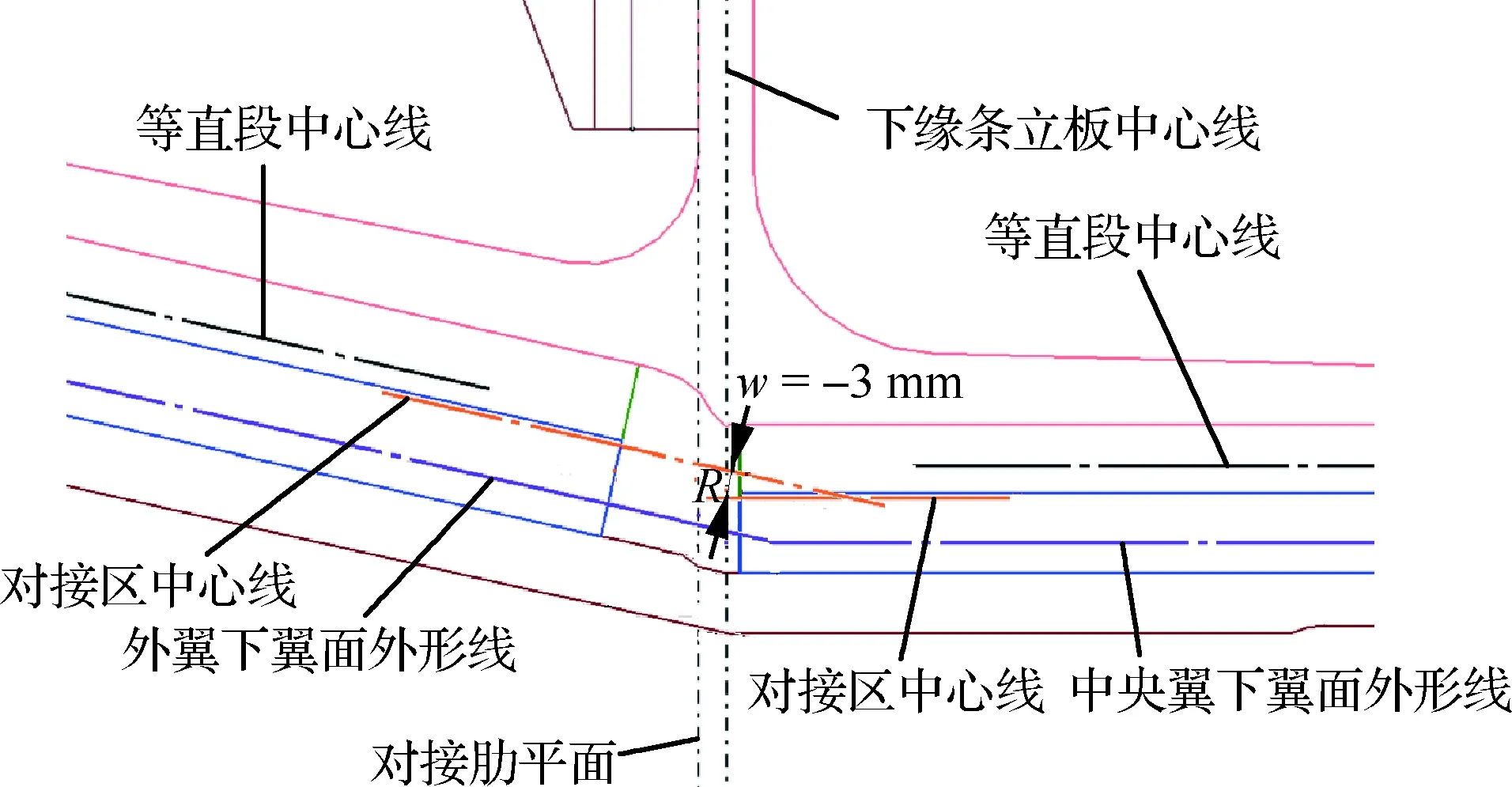
图20 4型对接组件偏心示意图Fig.20 Schematic of eccentric of No.4 butt-joint component
0型组件是基本型,是通常的骨架模型定义自然生成的。1型组件、2型组件是调整到一个特定位置生成的。3型组件、4型组件是分别从两个方向增加中央翼下壁板与外翼下壁板的错位,从而放大偏心距,以观察附加弯矩变化的。
3.2 分析结果
根据附加弯矩计算公式(1),分析组件的上反角α=12.5°,通常eWJ和eCWJcosα接近,外翼对接区和中央翼对接区的相对位置会明显影响附加弯矩的大小。
模型采用Hypermesh、ABAQUS进行分析,零件采用壳单元模拟(CQUAD4、CTRIA3),紧固件采用CBUSH/CBAR单元模拟,考虑接触(CGAPG),蒙皮和长桁缘条之间采用RBE2连接[13];外翼远端加载10 000.00 N,支持状态同图8 中所示;蒙皮和长桁按铝合金、肋腹板按铝合金、下缘条和对接带板按钛合金。钛合金切削粘刀严重,工艺性较差[14],飞机上经常用在关键连接区的接头上。
3.2.1 有限元法结果
1型对接组件的w=0,此时Δ=1.07 mm。分析后的组件位移见图21,图21(b)是图21(a)局部放大结果。
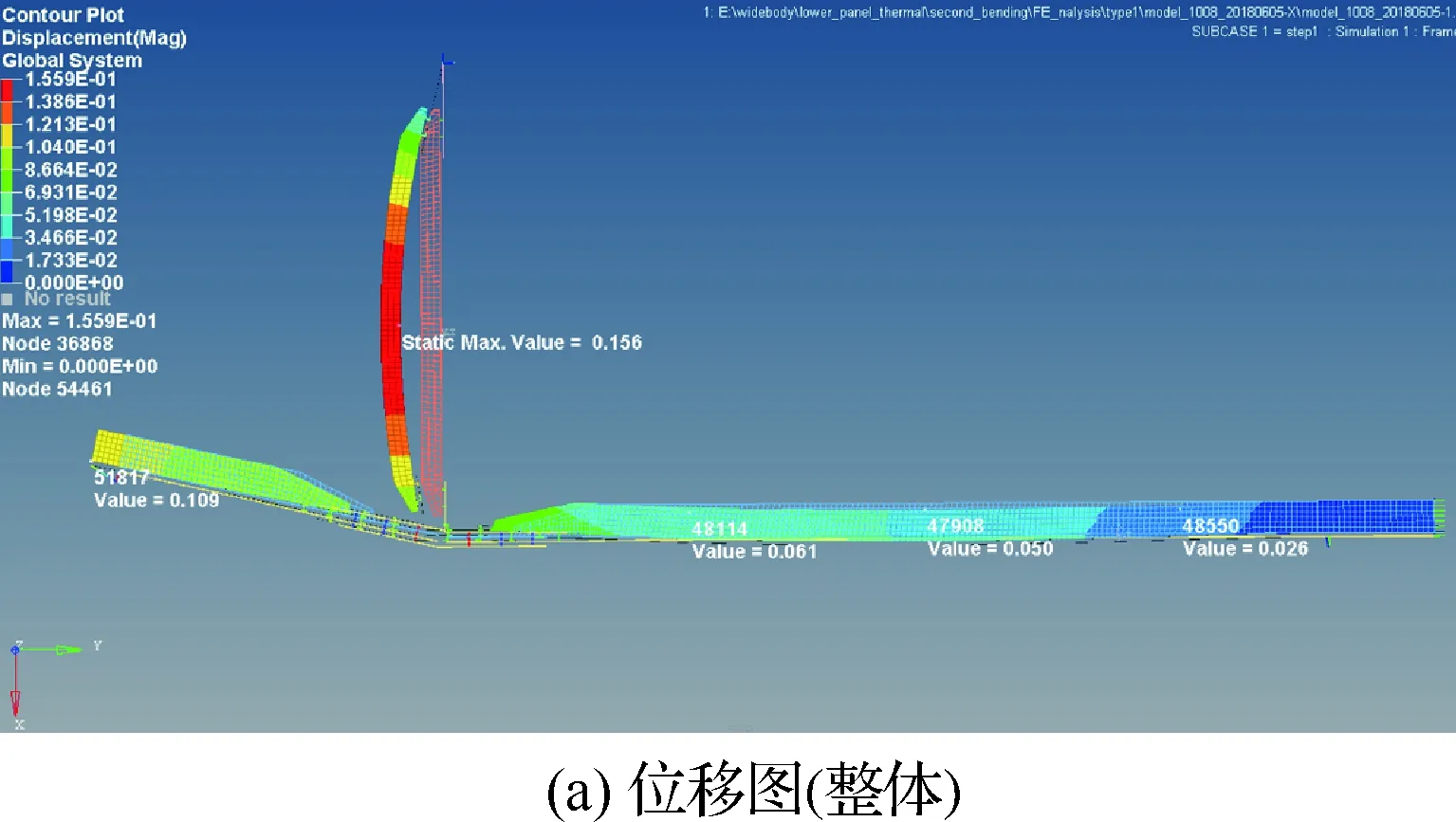
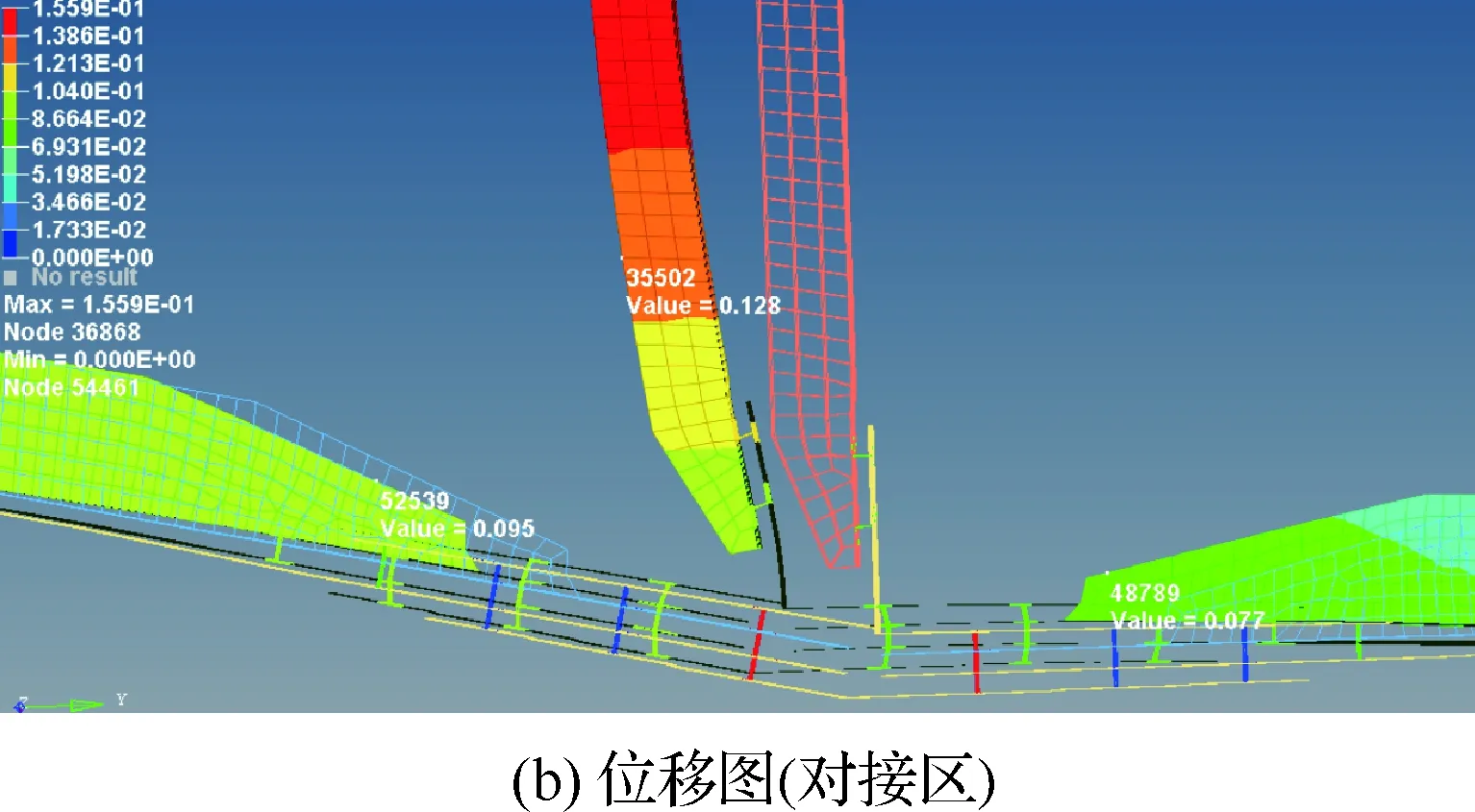
图21 1型对接组件位移Fig.21 Displacement of No.1 butt-joint component
从图21(b)中可见1型对接组件的变形和图16中力法分析的类似。
2型对接组件的w=0.76 mm,此时Δ=1.83 mm, 分析结果见图22。变形量较1型组件增大。
3型对接组件和2型对接组件类似,偏心方向相同,只是偏心量更大,Δ值也更大。变形位移也较2型组件更大。
4型对接组件的偏心方向和1型、3型的相反,分析结果见图23。
因为3型和4型对接组件是在5种分析组件中2个方向上的极限位置,3型和4型对接组件的Δ分别为4.07和-1.93 mm,外翼下壁板在对接区的偏心方向相反,计算出的外翼局部弯矩差别较大,变形也明显不同,变形后的位置相对于原位置见图24。

图22 2型对接组件位移(对接区)Fig.22 Displacement of No.2 butt-joint component (butt-joint aera)

图23 4型对接组件位移(对接区)Fig.23 Displacement of No.4 butt-joint component (butt-joint aera)
相对与0型对接组件(Δ=-0.1 mm),其余4种组件的Δ距离0变远了,附加弯矩也变大了,其中4型对接组件和0型对接组件一样附加弯矩为负值。
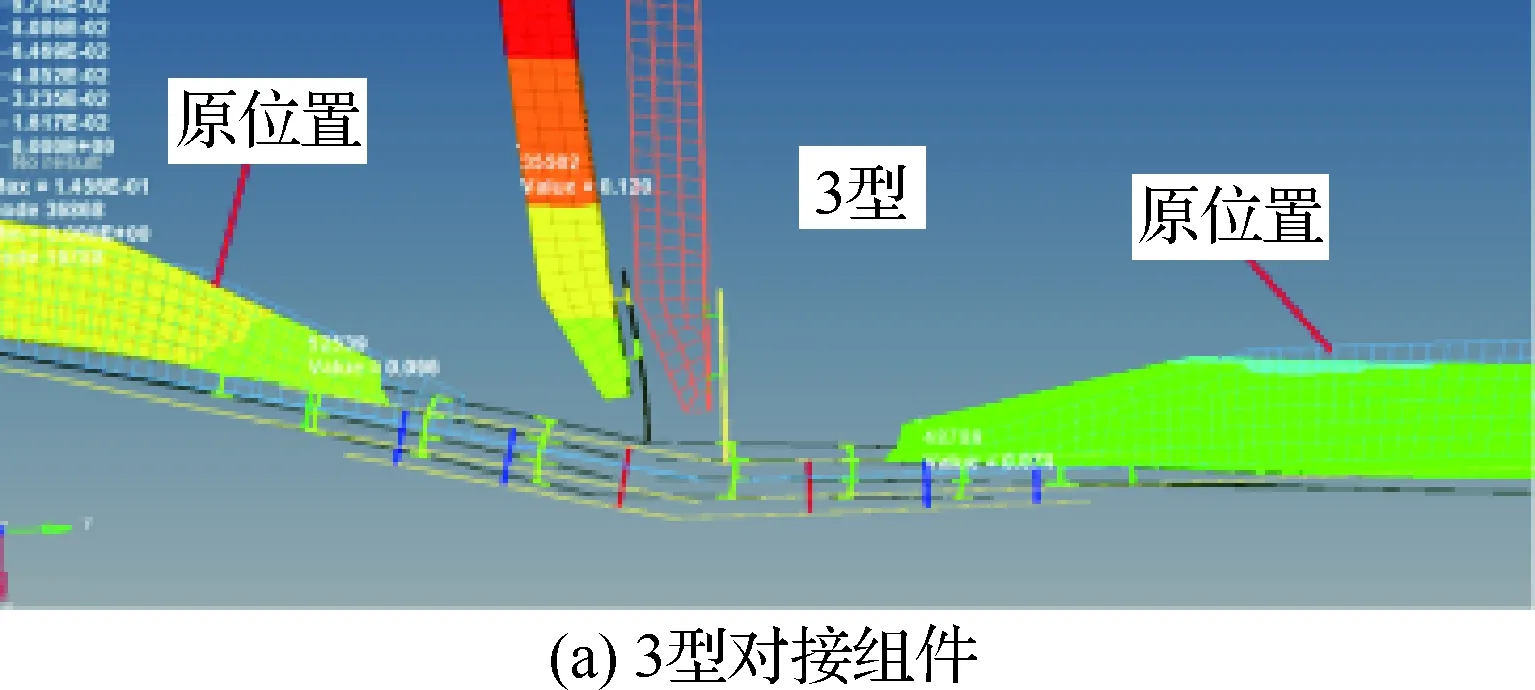
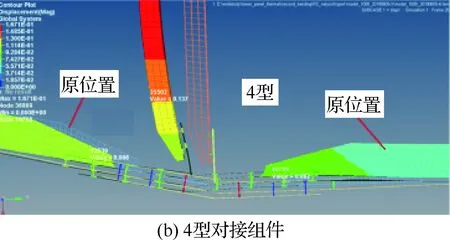
图24 3型和4型对接组件变形对比Fig.24 Comparison of deformations between No.3 and No.4 butt-joint components
3.2.2 有限元法和力法对比
对4组组件也用力法进行计算,因为力法未考虑紧固件和组件加载中的变形,和有限元法的具体数值还是有所不同。
0~4型共5组组件的力法和有限元法结果见表2。
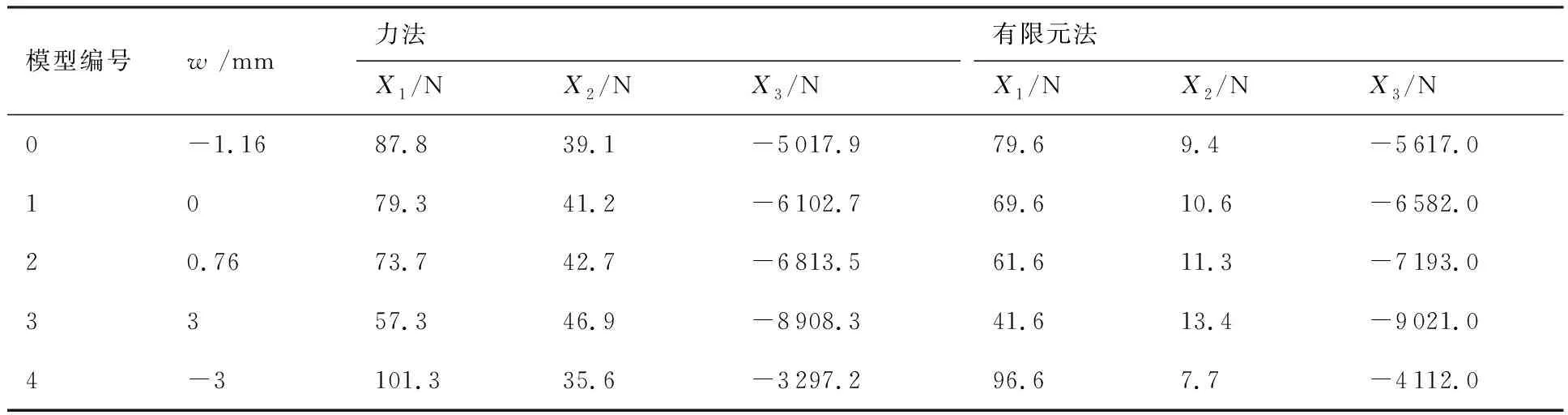
表2 2种算法的X1、X2、X3值Table 2 Values of X1,X2 and X3 under two algorithms
X1、X2和X3的有限元法和力法的对比见图25。
两种算法的结果显示趋势基本相同,X1、X3也基本近似,但X2的值相差较大,原因是分析模型中的支持点距离对接区很远,在加载过程中,组件的变形对各处支反力的影响用力法难以精确计算。有限元法的结果应更加符合实际情况。
两种算法显示随着对接区偏心距w的变动量增大,对接区结构相互间变形的变动量也加大,但离开对接区的下壁板等直段变形的变动量差别较小,这是因为从外翼下壁板加载端到中央翼下壁板龙骨梁支持端距离很大,对接区结构间的相互位置的很小改变不能影响大范围的变形分布。但对对接区结构来说,优化中央翼下壁板结构相对于外翼下壁板的位置,使得Δ、eW、eCW都尽量小,从而区域附加弯矩尽量小。这样可以使得区域传力更顺畅、局部不良变形更少、局部应力集中更少,是非常有实际意义的。
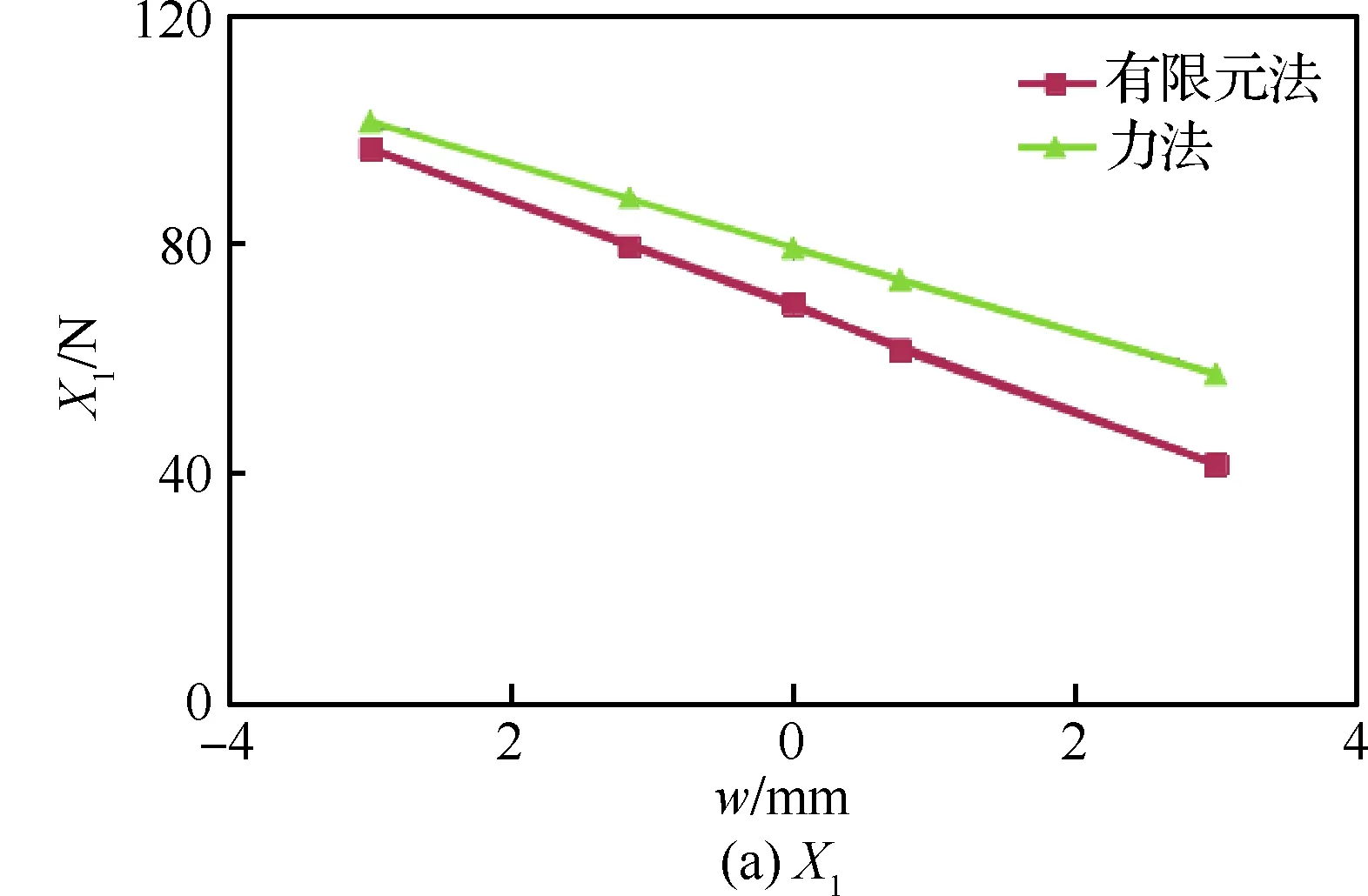
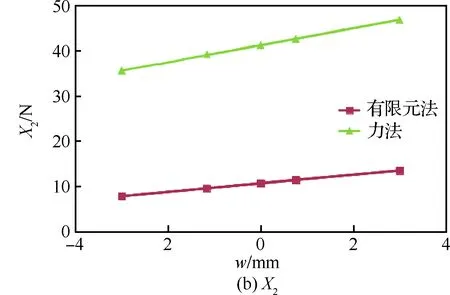
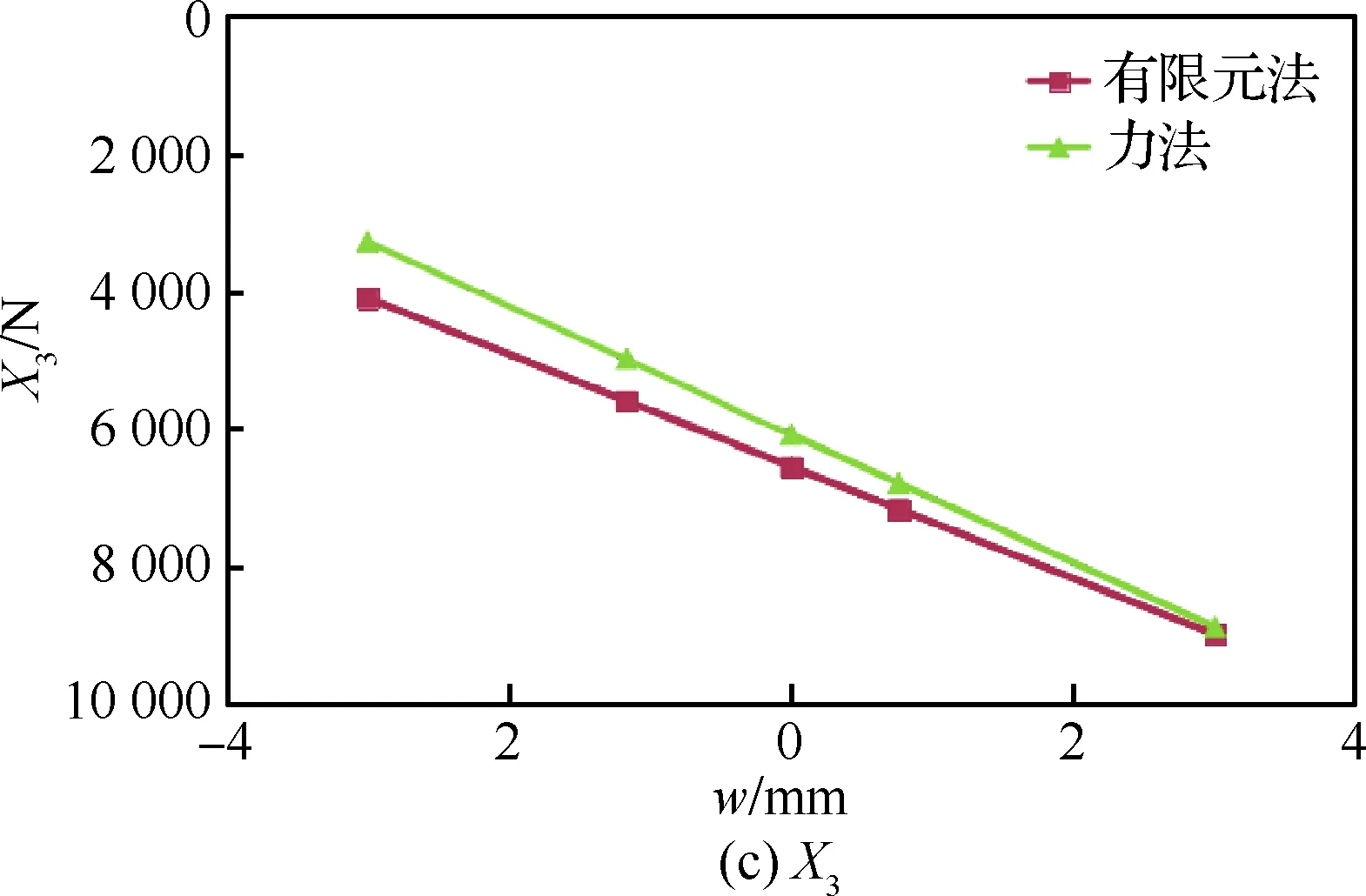
图25 有限元和力法对比Fig.25 Comparison between finite element method and force method
4 其他形式下壁板对接结构的附加弯矩
4.1 波音787飞机
波音787飞机的机翼下壁板长桁是“工”形,1号肋下缘条是“土”形,其下壁板对接结构与插入式完全不同。传力路径也完全不同,分成上、下两路传力。下壁板等直段中心线到对接区中心线变化很小,局部附加弯矩小;但外翼对接区中心线和中央翼对接区中心线依然有一定的偏心距,会造成对接区的附加弯矩。与插入式对接结构不同的是,附加弯矩对长桁端头的腹板影响较小,因为波音787下壁板长桁的“工”形上部与下缘条耳片连接,长桁腹板在上、下端都受到支持,即使附加弯矩使长桁端头产生弯曲和扭曲的趋势,但长桁腹板不容易产生分层。反而是长桁的“工”形下部,没有加宽加厚,处于对接区刚度变化较大的位置,在附加弯矩的影响下容易和蒙皮之间产生脱胶或撕裂,故而其在长桁端头的“工”形下部缘条上布置了加强垫片和止裂铆钉[15],见图26。
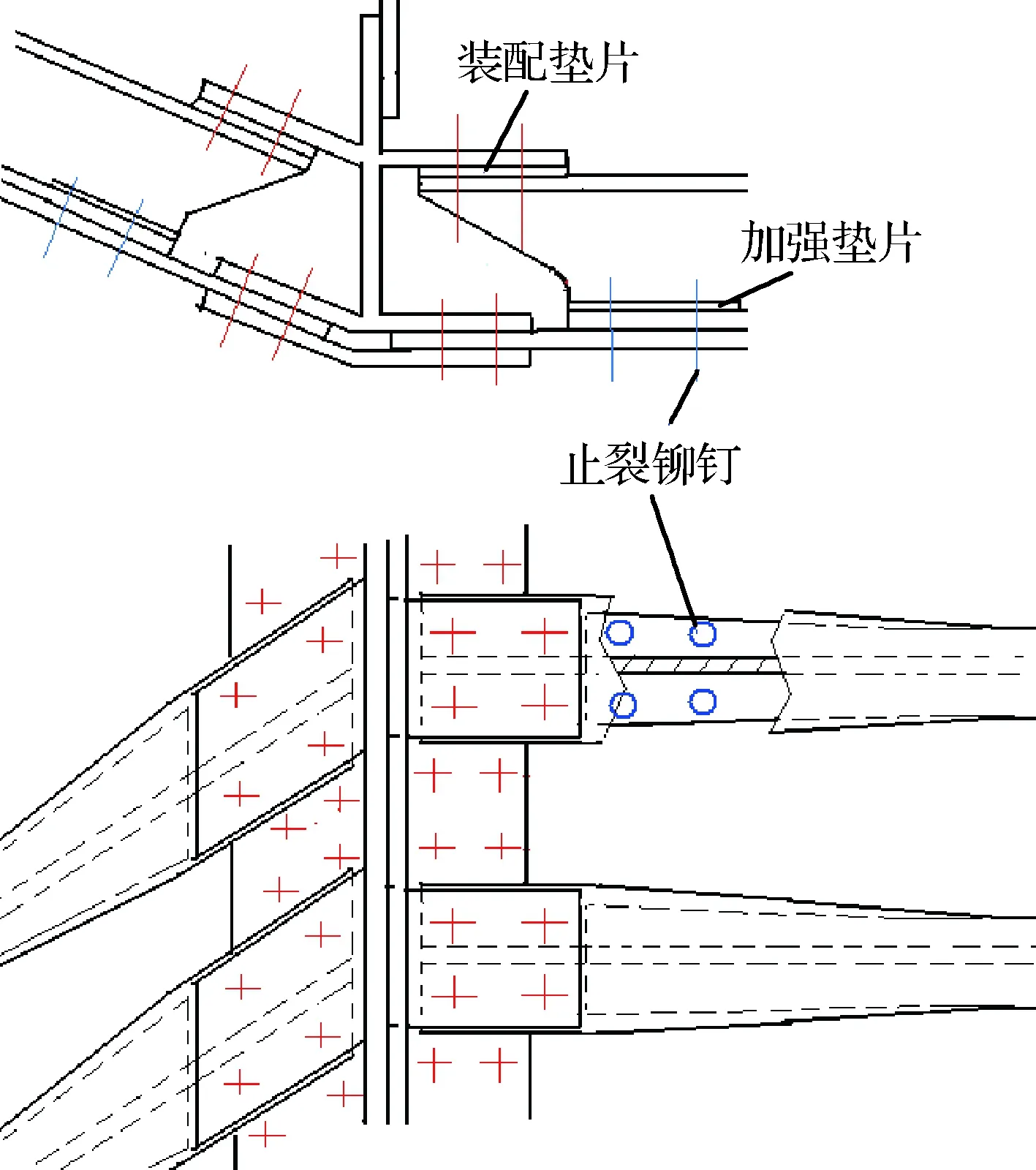
图26 波音787飞机下壁板对接结构Fig.26 Butt-joint structure of lower panel of Boeing 787
4.2 庞巴迪C系列飞机
庞巴迪C系列飞机的下壁板长桁是“T”形,下缘条是“T”形,其下壁板对接结构与插入式类似。传力路径相同,只有一路传力。不同的是其下缘条不开槽,长桁腹板不进入下缘条。其下壁板等直段中心线到对接区中心线的变化幅度相对于2.1节中典型的插入式结构更大,即局部附加弯矩更大。其外翼对接区中心线和中央翼对接区中心线的偏心量和典型插入式结构类似,即有一定的对接区附加弯矩。由于其长桁腹板的斜削段在下缘条之外,且下缘条展向只连接两排钉(下缘条侧边沿较厚),这样对接结构在下缘条侧边沿处会形成相对明显的刚度变化,附加弯矩会使长桁端部产生弯曲和扭曲的趋势,容易造成长桁缘条与蒙皮之间脱胶、撕裂和长桁腹板分层。庞巴迪C系列在长桁端头下缘条上布置有止裂铆钉[16],同时在长桁端头布置牺牲层,可对长桁缘条和长桁腹板起到保护作用,见图27。
通过以上分析,可知波音787飞机的下壁板对接结构受附加弯矩的影响较小,但其“工”形长桁,“土”形下缘条会使得制造和装配较复杂[17]。庞巴迪C系列飞机的类插入式对接结构受附加弯矩的影响较大,但其“T”形长桁,“T”形下缘条(且不开槽),使得制造和装配较简单,大量使用机器人铆接系统[18]。
典型插入式下壁板对接结构的制造性、装配性和附加弯矩的影响程度处于两机型之间,比较均衡。长桁缘条被对接结构3~4排钉夹持,较稳固,容易受附加弯矩影响的是长桁腹板。但插入式对接结构的传力更加稳定顺畅,如能减小其对接区的附加弯矩,将使得插入式对接结构更具有优点。
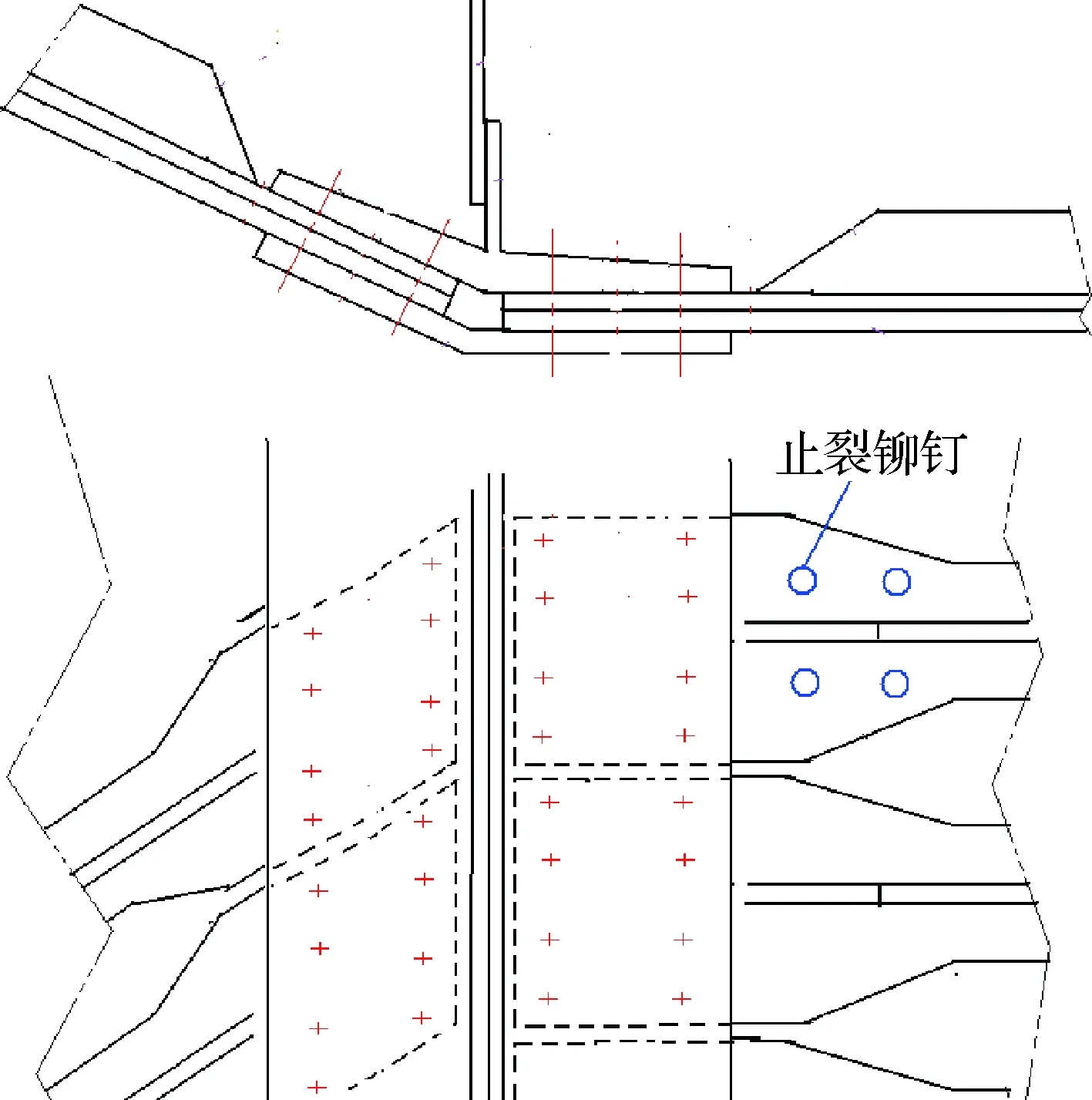
图27 庞巴迪C系列飞机下壁板对接结构Fig.27 Butt-joint structure of lower panel of Bombardier type C plane
5 结 论
本文提出了减小对接区及局部附加弯矩的方法,并分析了减小区域附加弯矩的影响。
1) 在中央翼骨架模型定义时,即根据计算有针对性地优化(抬高或降低)中央翼下翼面的外形面,使得对接区附加弯矩尽量小。通过力法和有限元法对模型的计算分析,证明减小对接区附加弯矩的方法有效、可行。
2) 采用相对强的蒙皮和相对弱的长桁(如降低长桁腹板高度),以减小下壁板等直段到对接区的中心线变化,从而减小局部附加弯矩。这样也有利于局部(长桁)破损安全,但这种布置对下壁板稳定性有所削弱,须考虑。
3) 对接区蒙皮和长桁缘条的加厚尽量平缓过渡。对于复合材料,剔层斜率不大于1∶40。
4) 需要特别注意长桁端头的保护性设计,如长桁腹板斜削转折处平缓过渡,复合材料的长桁还应布置牺牲层对斜削边的分层加以保护。
5) 1号肋腹板和下缘条立板连接区有一定的附加弯矩,应使用抗拉型紧固件;腹板边沿连接区适当加厚。
6) 下壁板对接区是载荷大的疲劳敏感区,插入式对接结构的典型双剪形式符合疲劳要求;减小此对接结构容易产生的附加弯矩能扬长避短,使得设计更加合理有效。
