圆锥曲线核心考点测试卷A
2019-03-02河南省项城市第一高级中学田大鹏
■河南省项城市第一高级中学 田大鹏
一、选择题
1.顶点在原点,经过圆C:x2+y2-2x+2 3y=0的圆心且准线与x轴垂直的抛物线的方程为( )。


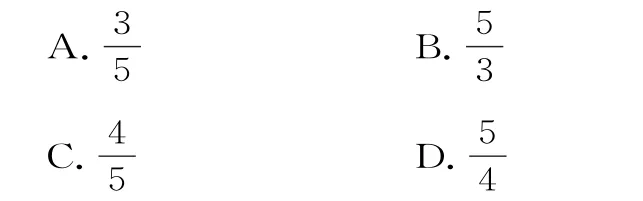
4.某些首饰,如手镯、项链、吊坠等都是椭圆形状,这种形状给人以美的享受,在数学中,我们把这种椭圆叫作“黄金椭圆”,其离心率设黄金椭圆的长半轴,短半轴,半焦距分别为a,b,c,则a,b,c满足的关系是( )。
A.2b=a+c B.b2=a c
C.a=b+c D.2b=a c
5.动圆C经过点F(1,0),并且与直线x=-1相切,若动圆C与直线y=总有公共点,则圆C的面积( )。
A.有最大值8 π B.有最小值2 π
C.有最小值3 π D.有最小值4 π
6.如图1,已知|A B|=10,图中的一系列圆是圆心分别为A、B的两组同心圆,每组同心圆的半径分别是1,2,3,…,n,…。利用这两组同心圆可以画出以A,B为焦点的椭圆或双曲线。若其中经过点M,N的椭圆的离心率分别是eM,eN,经过点P,Q的双曲线的离心率分别是eP,eQ,则它们的大小关系是( )。椭圆
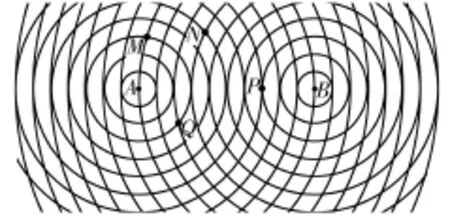
图1
A.eM<eN<eQ<eP
B.eN<eM<eP<eQ
C.eP<eQ<eM<eN
D.eQ<eN<eM<eP
7.已知p:“|a|=2”,q:“直线y=a x+1-a与抛物线y=x2相切”,则p是q的( )。
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
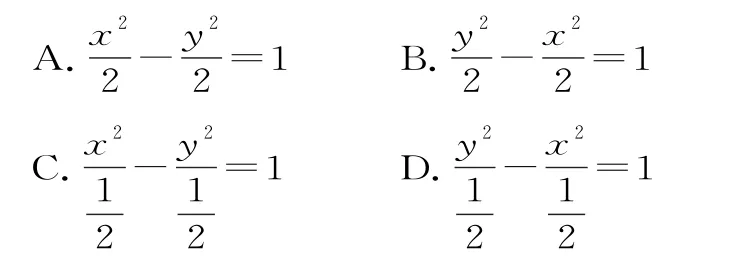
9.打开“几何画板”软件进行如下操作:
①用画图工具在工作区画一个大小适中的圆C;
②用取点工具分别在圆C上和圆C外各取一个点A,B;
③用构造菜单下对应命令作出线段A B的垂直平分线l;
④作出直线A C。
设直线A C与直线l相交于点P,当点B为定点,点A在圆C上运动时,点P的轨迹是( )。
A.圆 B.椭圆
C.双曲线 D.抛物线
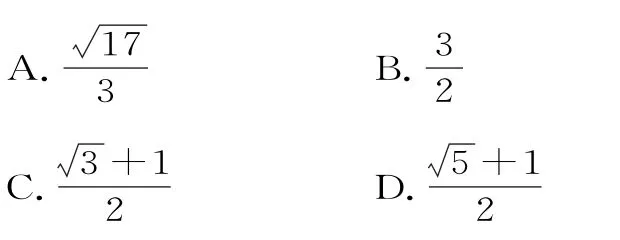
10.在△A B C中,A(x,y),B(-2,0),C(2,0),给出△A B C满足的条件,就能得到动点A的轨迹方程,如表1给出了一些条件及方程:

表1
则满足条件①、②、③的轨迹方程分别用代号表示应为( )。
A.E3,E1,E2B.E1,E2,E3
C.E3,E2,E1D.E1,E3,E2
二、填空题
13.已知水平地面上有一篮球,在斜平行光线的照射下,其阴影为一椭圆(如图2),在平面直角坐标系中,O为原点,设椭圆的方程,篮球与地面的接触点为H,则|OH|
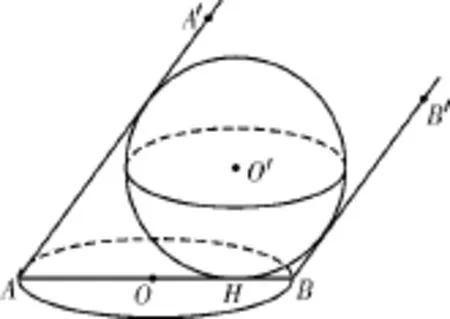
图2
14.设F为椭圆的右焦点且椭圆上至少有10个不同的点Pi(i=12,3,…),使|F P1|,|F P2|,|F P3|,…组成公差为d的等差数列,则d的取值范围是____。
15.从-3,-2,-1,1,2,3中任取三个不同的数作为椭圆方程a x2+b y2-c=0中的系数,则确定不同的椭圆的个数为____。
三、解答题
17.如图3所示,某街道居委会拟在E F地段的居民楼正南方向的空白地段A E上建一个活动中心,其中A E=活动中心东西走向,与居民楼平行。从东向西看活动中心的截面图的下部分是长方形A B C D,上部分是以D C为直径的半圆。为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长G E不超过2.5
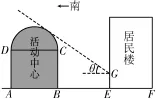
图3
(2)在保证上述采光要求的前提下,如何设计A B与A D的长度,可使得活动中心的截面面积最大?(注:计算中π取3)
18.图4所示的A-B-C-D-E-F是一个滑滑板的轨道截面图,其中A B,D E,E F是线段,B-C-D是一抛物线弧;点C是抛物线的顶点,直线D E与抛物线在D处相切,直线L是地平线。已知点B离地面L的高度是9m,离抛物线的对称轴的距离是6m,直线D E与L的夹角是45°。试建立直角坐标系:
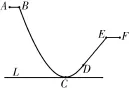
图4
(1)求抛物线方程,并确定D点的位置。
(2)现将抛物线弧B-C-D改造成圆弧,要求圆弧经过点B,D,且与直线D E在D处相切。试判断圆弧与地平线L的位置关系,并求该圆弧长。(可参考数据
19.设椭圆的一个顶点与抛物线C2:x2=4 3y的焦点重合,F1,F2分别是椭圆的左、右焦点,离心率,过椭圆右焦点F的直线与椭圆C交
2于M,N两点。
(1)求椭圆C的方程。
20.已知抛物线x2=4y,过抛物线上一点A(x1,y1)(不同于顶点)作抛物线的切线l,并交x轴于点C,在直线y=-1上任取一点H,过H作HD垂直x轴于点D,并交l于点E,过H作直线H T垂直于直线l,并交x轴于点T,如图5。
(1)求证:|O C|=|D T|;
(2)试判断直线E T与抛物线的位置关系,并说明理由。
21.已知椭圆C的两个焦点分别为F1(-1,0),F2(1,0),且F2到直线x-的距离等于椭圆的短轴长。
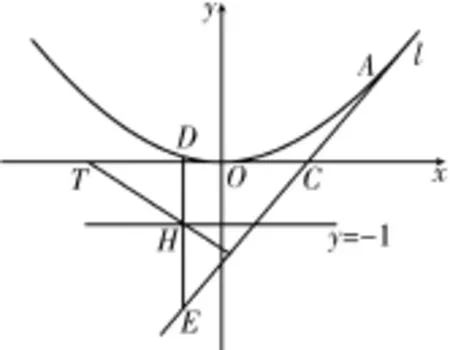
图5
(1)求椭圆C的方程;
(2)如图6,若圆P的圆心为P(0,t)(t>0),且经过F1,F2,Q是椭圆C上的动点且在圆P外,过Q作圆P的切线,切点为M,当|QM|的最大值为求t的值。

图6
(1)求椭圆的标准方程;
(2)设△A O B的面积为S,且|A B|=2,S=1,求直线A B的方程。
图7
